В сентябре 2023 года инженеры из гугла выпустили статью об использовании LLM для различных задач оптимизации. Там нет кода или ссылки на репозиторий, чтобы можно было самому поиграть, поэтому я написал простой оптимизатор с помощью языковой модели (Mistral-7B-Instruct) для задачи линейной регрессии.
Коротко о линейной регрессии
Линейная регрессия — это модель зависимости одной переменной от другой (или нескольких) с линейной функцией зависимости. Она позволяет предсказывать значение одной переменной на основании другой или нескольких.
Решить задачу линейной регрессии с одной переменной - значит нарисовать линию, которая будет максимально точно соответствовать существующим наблюдениям. Линия - это уравнение, подставив в которое значение X, мы получим предсказанное значение Y:
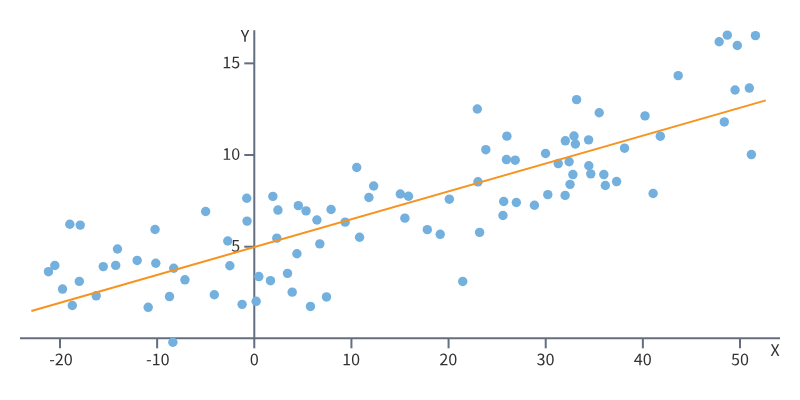
Чтобы оценить, насколько хорошо наша линия подходит под имеющиеся наблюдения, используют различные методы. Самый известный - метод наименьших квадратов (МНК). С его помощью мы определяем насколько далеко реальные наблюдения отдалены от нашей линии. Задача - минимизировать эти расстояния.
Функцию, которая рассчитывает расстояния, называют функцией потерь (loss function или cost function). И мы хотим её минимизировать.
Задача линейной регрессии имеет аналитическое решение. Когда с помощью манипуляций с производными мы получаем явную формулу и находим точное решение (правильную линию). Но если переменных и наблюдений слишком много, то аналитическое решение может быть вычислительно-затратным или даже невозможным.
Тогда на помощь приходят итерационные методы. Самый известный - градиентный спуск.
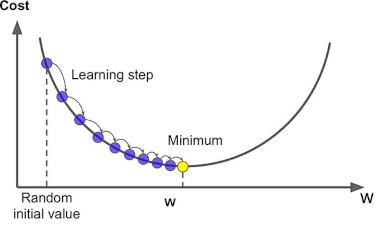
Во время градиентного спуска мы как бы проверяем: если я немного увеличу значение переменной w, то будет ли моя линия лучше подходить под имеющиеся наблюдения? Если да, то я немного увеличиваю w, если нет - уменьшаю. И так двигаюсь до тех пор, пока не окажусь в оптимальном минимуме.
Думаю, что-то похожее будет делать наша языковая модель, когда будет подбирать идеальные коэффициенты на основании только текстовых инструкций.
Больше про линейную регрессию - тут.
Про градиентный спуск - тут.
Функцию потерь - тут.
Оптимизируем с помощью LLM
Пайплайн:
Создадим набор данных со значениями y, x;
Случайно инициируем веса (w, b) для нашей линии y_pred = w*x + b;
Передадим модели инструкцию, в которой скажем, какое значение принимает наша функция потерь при заданных w, b. И попросим её изменить w, b таким образом, чтобы уменьшить функцию потерь. (Модель не будет знать, какую функцию мы оптимизируем. Мы будем подавать ей только значения: w, b, loss);
Возьмём предложенные моделью w, b, посчитаем для них loss и снова подадим модели. (Сначала на входе у модели будет всего один пример - случайно инициированные веса, а затем к нему буду добавляться примеры, которые она сама придумала, но не больше 10 штук);
Дождёмся, когда 3 последних значения loss функции станут меньше 1 и примем это за оптимальное решение.
Загружаем модель Mistral-7B-Instruct-v0.1 с Hugging Face:
import torch
from transformers import AutoModelForCausalLM, AutoTokenizer
device = "cuda"
model = AutoModelForCausalLM.from_pretrained("mistralai/Mistral-7B-Instruct-v0.1",
device_map=device,
torch_dtype=torch.bfloat16)
tokenizer = AutoTokenizer.from_pretrained("mistralai/Mistral-7B-Instruct-v0.1")Создадим набор данных:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
x = np.arange(0, 6, 0.5) # создаём истинные значения для x
y = 3*x + np.random.randint(-1, 2, 12) # создаём истинные значения для y + шум
# инициируем случайные веса для нашей линии y_pred = w*x + b
# во время оптимизации мы будем менять веса w, b, рассчитывать y_pred
# и сравнивать их с истинными значениями "y", определёнными выше
w = np.random.uniform(-5, 5)
b = np.random.uniform(-5, 5)Построим график:
fig, ax = plt.subplots()
ax.scatter(x, y)
ax.plot(x, w*x + b, c='red')
ax.set_xlabel('x')
ax.set_ylabel('y');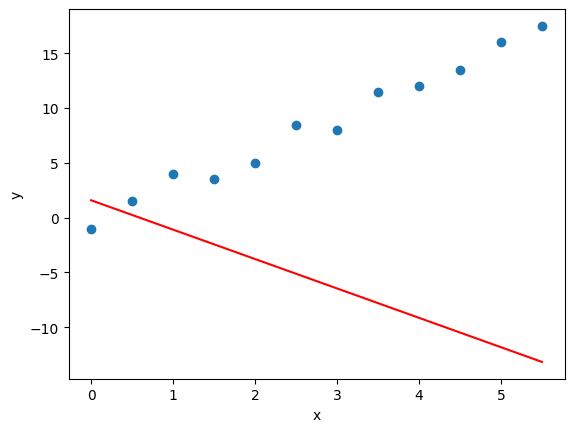
Красная линия - наш ответ со случайно инициированными весами (w, b).
Выглядит не очень.
Напишем несколько функций для парсинга ответов LLM, расчёта loss:
def is_number_isdigit(s): # парсинг str ответа от LLM
n1 = s[0].replace('.','',1).replace('-','',1).strip().isdigit()
n2 = s[1].replace('.','',1).replace('-','',1).strip().isdigit()
return n1 * n2
# останавливаем оптимизацию, когда последние "last_nums" значений loss < 1
def check_last_solutions(loss_list, last_nums):
if len(loss_list) >= last_nums:
last = loss_list[-last_nums:]
return all(num < 1 for num in last)
def loss_calc(y, w, x, b):
return ((y - w*x + b)**2).mean() # функция потерь МНК
loss = loss_calc(y, w, x, b) # рассчитаем первый loss для случайных (w, b)
d = {'loss': [loss], 'w': [w], 'b': [b]}
loss_list = [loss] # соберём все loss для построения графика в конце
df = pd.DataFrame(data=d) # датасет c предложеными моделью весами (w, b) и loss
df.sort_values(by=['loss'], ascending=False, inplace=True)Посмотрим loss со случайно инициированными w, b:
dfOutput:
loss w b
404.096928 -2.683655 1.586905Создаём промт:
# num_sol - максимальное кол-во наблюдений в промте
def create_prompt_bias(num_sol):
meta_prompt_start = f'''Now you will help me minimize a function with two input variables w, b. I have some (w, b) pairs and the function values at those points.
The pairs are arranged in descending order based on their function values, where lower values are better.\n\n'''
solutions = ''
if num_sol > len(df.loss):
num_sol = len(df.loss)
for i in range(num_sol):
solutions += f'''input:\nw={df.w.iloc[-num_sol + i]:.3f}, b={df.b.iloc[-num_sol + i]:.3f}\nvalue:\n{df.loss.iloc[-num_sol + i]:.3f}\n\n'''
meta_prompt_end = f'''Give me a new (w, b) pair that is different from all pairs above, and has a function value lower than
any of the above. Do not write code. The output must end with a pair [w, b], where w and b are numerical values.
w, b ='''
return meta_prompt_start + solutions + meta_prompt_end# Вот так будет выглядеть промт для двух решений.
# Значения сотрируются по loss(value) по убыванию.
Now you will help me minimize a function with two input variables w, b. I have some (w, b) pairs and the function values at those points.
The pairs are arranged in descending order based on their function values, where lower values are better.
input:
w=-0.456, b=0.357
value:
135.314
input:
w=0.700, b=0.450
value:
63.494
Give me a new (w, b) pair that is different from all pairs above, and has a function value lower than
any of the above. Do not write code. The output must end with a pair [w, b], where w and b are numerical values.
w, b =Запускаем цикл оптимизации:
num_solutions = 10 # кол-во наблюдений, которое будем подавать в промт
for i in range(500):
text = create_prompt(num_solutions)
model_inputs = tokenizer([text], return_tensors="pt").to(device)
model.to(device)
generated_ids = model.generate(
**model_inputs,
max_new_tokens=15,
temperature=0.8,
do_sample=True,
pad_token_id=50256
)
output = tokenizer.batch_decode(generated_ids)[0]
response = output.split("w, b =")[1].strip()
if "\n" in response:
response = response.split("\n")[0].strip()
if "," in response:
numbers = response.split(',')
if is_number_isdigit(numbers):
w, b = float(numbers[0].strip()), float(numbers[1].strip())
loss = loss_calc(y, w, x, b)
loss_list.append(loss)
new_row = {'loss': loss, 'w': w, 'b': b}
new_row_df = pd.DataFrame(new_row, index=[0])
df = pd.concat([df, new_row_df], ignore_index=True)
df.sort_values(by='loss', ascending=False, inplace=True)
if i % 20 == 0: # принтуем каждый 20-ый шаг
print(f'{w=} {b=} loss={loss:.3f}')
if check_last_solutions(loss_list, 3):
breakOutput:
w=-100.0 b=1.0 loss=112593.792
w=-1.5 b=0.9 loss=245.704
w=2.2 b=1.1 loss=15.197
w=-2.0 b=-1.0 loss=246.792
w=3.5 b=1.2 loss=0.809Посмотрим последние 10 значений loss:
print(*loss_list[-10:], sep='\n')44.41708333333333
28.161666666666665
26.42833333333333
21.763333333333335
46.583333333333336
20.939537499999997
20.939537499999997
0.80875
0.80875
0.6437500000000002А вот так теперь выглядит наша прямая:
fig, ax = plt.subplots()
ax.scatter(x, y)
ax.plot(x, w*x + b, c='red');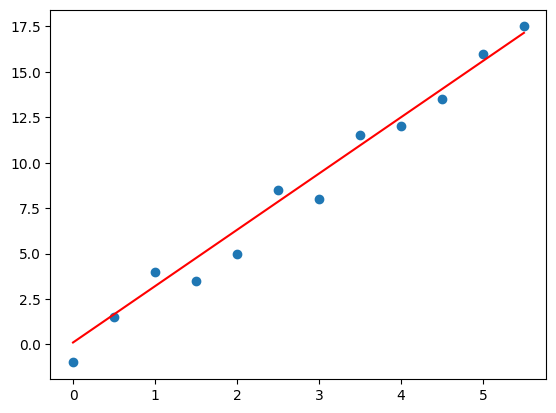
Посмотрим на снижение loos во время оптимизации (ограничил значения 700 единицами, потому что в процессе тренировки было несколько выбросов со значениями больше миллиона).
fig, ax = plt.subplots()
print(f'number of step = {len(loss_list)}')
ax.plot([x for x in loss_list if x < 700]);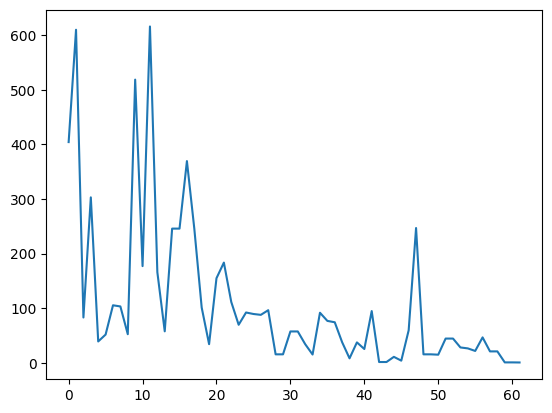
Интересное наблюдение. Температура (temperature), параметр, который отвечает за вариативность ответов модели, играет в нашем случае своеобразную роль шага для градиентного спуска. Чем ниже температура, тем медленнее снижается loss, но в то же время реже встречаются выбросы. И наоборот - чем выше температура, тем более уверенные "шаги" делает модель, быстрее сходится, но и часто отдаёт большие выбросы.
Вот так, например, выглядит снижение loss при temperature=0.5 через каждые 20 итераций:
w=-0.001 b=2.73 loss=153.029
w=0.0 b=2.73 loss=152.950
w=1.0 b=2.73 loss=83.893
w=0.333 b=1.73 loss=108.150
w=0.5 b=1.73 loss=97.242
w=0.94 b=1.73 loss=71.318
w=0.97 b=1.75 loss=69.999
w=0.995 b=1.715 loss=68.143
w=0.999 b=1.719 loss=67.990
w=0.999 b=1.719 loss=67.990
w=0.999 b=1.719 loss=67.990
w=0.999 b=1.719 loss=67.990
w=0.719 b=0.2 loss=61.172
w=0.75 b=0.15 loss=58.963
w=0.852 b=0.1 loss=53.394
w=0.905 b=0.095 loss=50.863
w=0.918 b=0.078 loss=50.063
w=0.922 b=0.068 loss=49.762
w=0.931 b=0.063 loss=49.294
w=0.936 b=0.056 loss=48.985
w=0.935 b=0.057 loss=49.042
w=0.939 b=0.054 loss=48.826
w=0.939 b=0.054 loss=48.826
w=0.946 b=0.051 loss=48.475
w=0.934 b=0.043 loss=48.922P. S.
Не стоит рассматривать языковую модель, как реальный инструмент для оптимизации в таких задачах. Для решения задачи линейно регрессии существуют куда более простые, быстрые и менее затратные методы (для запуска Mistral-7B-Instruct в формате bfloat16 требуется видеокарта с памятью как минимум 16Gb).
Но в целом тенденция выглядит немного пугающей. Даже относительно небольшие LLM становятся всё более "умными", а люди находят им всё новые применения. Например, в статье, на которую я ссылался вначале, авторы предлагают метод оптимизации промтов - а это уже реальная заявка на то, чтобы отобрать работу у промт инженеров (ну или по крайней мере внести существенные коррективы в их обучение).
Репозиторий с кодом на GitHub - https://github.com/akocherovskiy/LLM_as_optimizer
Google Colab, где можно запустить код на бесплатной Т4 - LLM_as_optimizer
Комментарии (6)

AnonimYYYs
16.10.2023 07:54Вот когда хотя бы что нибудь смешанное из двух базовых функций (синус+квадрат например) сможет оптимизировать на задаче из миллиона точек - тогда и поговорим. А на основе решения того, что и ребенок осилит руками делать выводы о "пугающей тенденции" - ну камон, не слишком серьезно

akocherovskiy Автор
16.10.2023 07:54Согласен, что пример слишком простой. Но посмотрим, как оно будет.

DungeonLords
16.10.2023 07:54Больше про линейную регрессию - действительно на википедии. Кстати я являюсь автором иллюстрации. Эта иллюстрацию сгенерирована программой. Буду рад комитам, там есть что улучшить. В частности я думаю добавить опционально включение сетки... Также надо подумать что происходит с длинной линии...
Example

neowisard
16.10.2023 07:54Всегда было интересно какие прикладные применения могут быть у таких задачек ?
Как определяют при R&d что нужна такая оптимизация ? Берут в команду человека который погружён в математику или заказывают институту исследование?



uchitel
Это уже не тенденция, а более-менее обозначенная потребность бизнеса. В последней книге по RL (автора увы сейчас не вспомню, но на книге нарисован пингвин) автор во введении прямо пишет, что некоторые компании рассматривают RL, как способ сокращения штата ML инженеров.
Еще мне попадалось несколько статей схожей тематики. В одной из них рассматривалось обучение оптимизации, причем так же на примере регрессионных моделей. И оно работает. В другой хорошей обзорной статье рассматривалась применение RL (и ML по моему тоже) к задаче целочисленного линейного программирования.
Короче, надо налегать на RL.
akocherovskiy Автор
Многие новые языковые модели облучаются на данных, сгенерированных другими языковыми моделями. Причём, для тех же instuct моделей, учёные просят LLM сначала написать задачу, потом просят её же эту задачу решить и на основании получившегося датасета тренируют новые модели) Так было с microsoft/phi вроде.