В этой статье я расскажу вам про 5 моих любимых нерёшенных задач, условие которых очень легко понять, однако очень трудно решить.
Эти задачи показались мне интересными, поэтому я решил написать про них статью. И нет, здесь не будет их доказательств.
1. Бинарная проблема Гольдбаха
Верно ли, что каждое чётное число, большее 2, можно представить в виде суммы двух простых чисел?
Это очень известная гипотеза, которая, однако, пока не решена.
Нам известно, что любое чётное число можно представить в виде 4 простых чисел, а любое нечётное - в виде трёх (см. Тернарная проблема Гольдбаха). Также эта гипотеза верна для всех чётных чисел, не превышающих
Доказано, что любое достаточно большое чётное число можно представить в виде суммы простого и полупростого числа (полупростое число - это произведение двух простых чисел).
Чем больше наше чётное число, тем, очевидно, больше вероятность, что его можно представить в виде суммы 2-х простых чисел. Ещё я написал небольшую программку, которая должна проверять гипотезу.
Вот код
#include <iostream>
#include <vector>
#include <algorithm>
// Программа проверяет справедливость гипотезы от 4 до х
int main() {
long long x = 1000000;
char arr[x];
std::vector<long> a = {};
arr[0] = '0';
arr[1] = '0';
for (long long i = 2; i < x; i++) arr[i] = '1';
long long s = 1;
for (long long i = 0; i < x; i++) {
if (arr[i] == '0') continue;
a.push_back(i);
for (long long j = i*i; j < x; j = j + i) arr[j] = '0';
}
for (long long i = 4; i < x; i+=2) {
for (long n:a) {
if (std::find(a.begin(), a.end(), i-n) != a.end()) {
if (n > 100) std::cout<<i<<"="<<n<<"+"<<i-n<<std::endl;
break;
}
}
}
};2. Гипотеза Била
Если , где
натуральные числа и
, то
имеют общий делитель.
За доказательство или опровержение этой гипотезы американский миллиардер Эндрю Бил положил приз в один миллион долларов.
Существует множество примеров решения этого уравнения, однако для них всех имеют общий делитель, например,
.
Гипотеза Била является обобщением Великой теоремы Ферма. Действительно, если гипотеза Била справедлива, и существуют такие наименьшие числа , что
, то, поскольку
имеют общий делитель, верно также и
, где
- это общий делитель трёх чисел. Но наши числа
не наименьшее, и мы пришли к противоречию.
То есть, если гипотеза Била справедлива, то тогда автоматически справедлива и Великая теорема Ферма, кстати говоря, доказанная в 1995 году.
На 2013 год гипотеза была проверена для случаев, когда все 6 чисел не превышают 1000.
Также справедливость гипотезы Била доказана при значениях , равных
, где
- любое натуральное число.
3. Бесконечность чисел-близнецов
Верно ли, что простых чисел-близнецов бесконечно много?
Простые числа-близнецы - это простые числа, разница между которыми равна 2. Например, числа 29 и 31 являются простыми числами-близнецами.
Доказано, что существует бесконечно много простых чисел, разница между которыми меньше, чем 246. Однако до двойки всё ещё далеко..
Самые большие известные простые числа-близнецы - это . Такое огромное число говорит в пользу гипотезы. Однако всё необходимо доказывать строго.
Известно, что если ряд ,где
- это k-тое простое число, сходится, то тогда гипотеза неверна.
Между прочим, иногда очень трудно понять, сходится ряд или расходится. Например, ряд расходится, однако даже если учесть все известные науке простые числа, сумма их обратных дробей (1/p) будет меньше четырёх!
4. Совершенный кубоид
Существуют ли такие натуральные числа ,для которых
и
являются квадратами натуральных чисел?
Если ответ "да", то тогда эти числа образуют рёбра совершенного кубоида, то есть прямоугольного параллелепипеда, у которого все рёбра, их диагонали, а также основная диагональ целые числа.
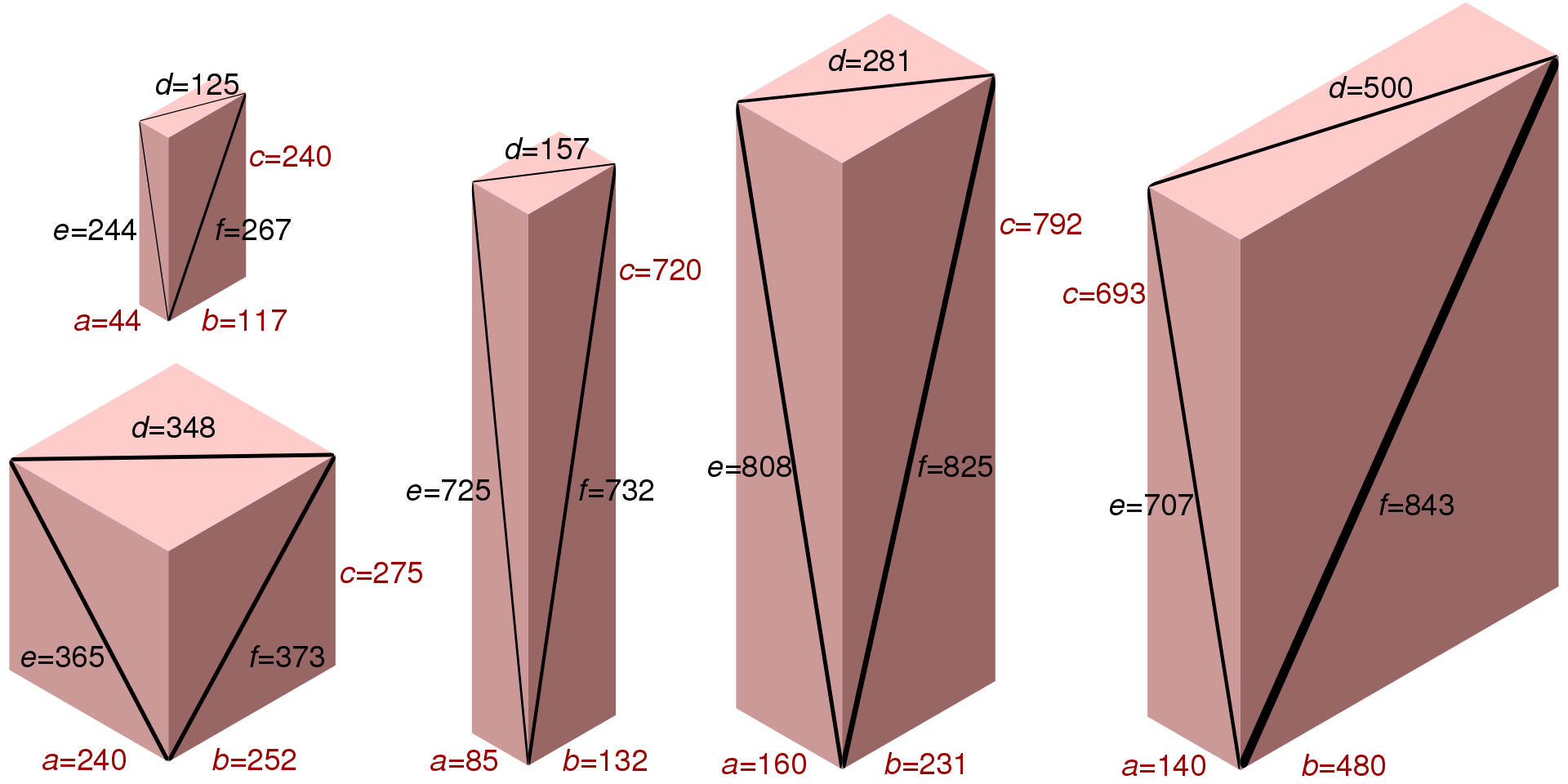
Прямоугольные параллелепипеды, рёбра и диагонали ребёр которых целые числа, называются параллелепипедами Эйлера. Например, таким параллелепипедом является параллелепипед с рёбрами 240, 117 и 44.
Действительно,
117^2 + 44^2 = 125^2;
240^2 + 44^2 = 244^2;
240^2 + 117^2 = 267^2
Однако чётвертое условие не выполняется: не является квадратом целого числа.
Если совершенный кубоид существует, он должен выполнять несколько условий:
Одно из чисел
делится на 4, другое на 16;
Одно из чисел
делится на 3, другое на 9;
Одно из чисел
делится на 5;
Одно из чисел
делится на 11;
Компьютерный перебор проверил все значения ребёр до , но пока никаких кубоидов не нашёл.
Однако, гипотезу это не опровергает.
5. Числа Серпинского
Если для любого натурального числа n число составное, то k является числом Серпинского. Верно ли, что 78557 наименьшее число Серпинского?
Да, может показаться удивительным, но такие числа существуют. Например, доказано, что всегда будет делиться либо на 3, либо на 5, либо на 7, либо на 13, либо на 19, либо на 37, либо на 73.
На данный момент известно лишь 5 чисел, меньших 78557, и которые могут быть числами Серпинского. Это 21881, 22699, 24737, 55459 и 67607.
Кстати, именно с числами Серпинского связано нахождение одного из самых больших простых чисел - речь идёт про .
Подумайте, если бы наука ограничилась бы только перебором n до 31172164, то она бы заявила, что 10223 является числом Серпинского. И была бы неправа.
Я считаю, что эта гипотеза учит нас, что перебор надо доводить до конца, а поспешных заявлений делать не стоит.
Комментарии (69)

Sarjin
28.10.2023 08:27-9известно ли чем/кому решение этих задач поможет?

StjarnornasFred
28.10.2023 08:27+4Гипотеза: доказательство или опровержение гипотезы о совершенном кубоиде имеет прикладное применение.
Статус: не доказана, не опровергнута.
Примерный план действий: сначала доказать или опровергнуть гипотезу о совершенном кубоиде, дальше действовать исходя из полученных данных.

niktor_mpt
28.10.2023 08:27-1Совершенный кубоид уже существует, потому что о нём задан вопрос. :)
Практическая польза - там, где мы вынуждены оперировать целым. Это не обязательно будет коробка, что угодно вот с такими вот параметрами и связями между ними.
Может, будет обобщение на н-мерное пространство. Может, даже на дробномерное. Чем плоха функция, возращающая true-false для n-мерного целочисленного параллепипеда и m<=n целочисленных диагоналей в нём? Если она будет конструктивной, т.е. давать набор(ы) целых чисел, вообще супер. Для инженеров.
Кстати, если будет алгоритм, быстро строящий хороший почти кубоид (т.е. длины отличаются от целых чисел меньше, чем на эпсилон, а их абсолютные величины минимальны), то это уже прикладникам работа. Для иррациональных чисел задачая наилучшего рационального приближения решена (цепные дроби).
А для чего он нужен в математике - вопрос к математикам. Дразниться своей нерешённостью:)

wataru
28.10.2023 08:27Совершенный кубоид уже существует, потому что о нём задан вопрос.
Совсем нет. Описаны какие-то свойства. Вопрос в том, а противоречивы ли эти свойства друг другу.

niccolo2019
28.10.2023 08:27Задачи конечно интересные, но чтобы их начали решать, находя приёмы, имеющие практическое значение, а не брать грубой вычислительной мощностью, математикам надо оставить доступ к компьютерам только для проверки верности или неверности их гипотез....
И исправьте ошибку в тексте
Однако чётвертое условие не выполняется:не является целым числом.????

BugM
28.10.2023 08:27+1Перебирают если доказать не могут. В конце концов часть задач можно решить найдя один контр пример. Попробовать найти такой пример перебором просто напрашивается.

wataru
28.10.2023 08:27Эти задачи не решить грубой вычислительной мощью, потому что они оперируют всеми числами. Перебор может помочь найти контр-пример, если он достаточно маленький, да убедить, что гипотеза скорее верна, чем нет. И имеет смысл бросать силы на математическое доказательство.

mahmud-podzhigai
28.10.2023 08:27147^2 + 44^2 = 125^2 - это же, очевидно, не выполняется
И у вас то 147, то 117 в задаче фигурирует

fish224 Автор
28.10.2023 08:27+1Там конечно же 117, просто я в темноте переписывал текст с бумаги в хабр, вот и получилась опечатка. Я уже исправил

KvanTTT
28.10.2023 08:27Гипотеза Била является обобщением Великой теоремы Ферма.
А abc-гипотеза, в свою очередь, является обобщением гипотезы Била.

Portnov
28.10.2023 08:27+2существование таких нерешённых задач, кажется, говорит, что мы чего-то очень главного не понимаем о том, как устроены числа. Ну сравните например с физикой: существуют, конечно, очень сложные утверждения (типа пресловутой "теории всего"), которые пока не доказаны и не опровергнуты; но речь идёт о глубинах глубин. Все физические задачи, условия которых может понять школьник, были решены 100 лет назад, если не раньше. А тут... некоторые из задач выглядят так, будто ребёнок спросил "почему трава зелёная", и величайшие умы мира столетиями не могут найти ответа.

torbasow
28.10.2023 08:27+6А мне кажется, что вот как раз главное в том, как устроены числа, мы поняли очень давно: «Один дурак может задать вопросы, на которые и сто мудрецов не ответят».
Дисклеймер: это не оскорбление.

sergeaunt
28.10.2023 08:27+7А один умный, у которого поля слишком узки, может так потроллить, что столетия спустя фрики будет осаждать математические кафедры с якобы его чудесным доказательством.

avost
28.10.2023 08:27+2Все физические задачи, условия которых может понять школьник, были решены 100 лет назад, если не раньше.
Ну, что вы! Буквально соседняя же тема - Могут ли в нашей Вселенной существовать магнитные монополи?

sena
28.10.2023 08:27Все физические задачи, условия которых может понять школьник, были решены 100 лет назад
Как возникла Вселенная? Как возникла жизнь? Бесконечна ли Вселенная? Какое физическое явление лежит в основе шаровой молнии? Как создать шаровую молнию? Что такое время? И это навскидку...

SergeyMax
28.10.2023 08:27Какое физическое явление лежит в основе шаровой молнии?
Судя по тому, что после повсеместного распространения смартфонов количество наблюдаемых шаровых молний свелось к нулю, основой шаровой молнии являлось физическое явление под названием п..дëж.

Feedman
28.10.2023 08:27Есть такой портал, youtube называется. Все эти "куда пропали НЛО, снежный человек" и прочие явления, переместились туда. Я отнюдь не утверждаю, что все эти "феномены" (кроме НЛО) существуют в природе, но видео с ними там вроде как предостаточно.

smrl
28.10.2023 08:27+1Атом из i протонов и j нейтронов - превращается в атом с i' протонов и j' нейтронов. Какова вероятность (доля) такого превращения? А его скорость (период полупревращения)?
Надеюсь, условие можно объяснить школьнику? А то очень нужно решение!

BugM
28.10.2023 08:27+3Все физические задачи, условия которых может понять школьник, были решены 100 лет назад, если не раньше
Любой школьник знает или может быстро понять что такое сверхпроводимость. Можно мне формулу по которой можно посчитать при каких условиях в указанном веществе будет/не будет возникать сверхпроводимость?

Dr_Faksov
28.10.2023 08:27Я ещё про радиоволны добавлю. Как электрический ток превращается туда и обратно.
Кстати, что такое электричество тоже можно спросить. Не электрический ток и электрическое поле, а вот это вот без слов "поле" и "ток".

BugM
28.10.2023 08:27+1Это скучно. Колебательный контур, электромагнитное поле. Все понятно и изучено.
Второе тоже скучно. Электроны, заряд, упорядоченное движение. Тоже давно изучено.
Если не знать школьных терминов и школьной физики, то любая наука становится магией. Не надо так. Лучше прочитать учебник. Он понятный.

Yamazaki123
28.10.2023 08:27+1В физике полно задач, которые формулируются очень просто, а решаются очень сложно. Скажем: есть замкнутая кубическая емкость размером 1*1*1м, заполненная водой. В её нижней стенке строго по центру проделано отверстие диаметром 20мм. Температура 20°C, давление 760мм.рт.ст. За сколько секунд вытечет вода?
Условия заданы просто, но поведение воды сложно (см. уравнения Навье-Стокса). Ни в одном учебнике нет для такой задачи подходящей формулы, придется решать численным моделированием, медленно и мучительно.

arTk_ev
28.10.2023 08:27Да, поэтому ввели теорию множеств и функан.Там нет цифр, это низкоуровневая математика.
Более важная проблема в математике - это проблема нелинейности. Нелинейность порождает бесконечность и хаос. В материальном мире линейных процессов вообще не существует. А математики еще не научились решать нелинейные деферициальные уравнения даже второго порядка, только числено.

Alexandroppolus
28.10.2023 08:27+1Как в эту копилку не попала наша любимая задача "3N+1"? По количеству убитых человекочасов и сгоревших пуканов она уступает разве только самой ВТФ.

DieselMachine
28.10.2023 08:27+1Существует ещё обобщение проблемы Гольдбаха, которое утверждает, что любое чётное число, большее чем 4208, представляется в виде суммы двух простых близнецов. Таким образом если будет доказано это обобщение, то отсюда сразу следует и проблема Гольдбаха, и бесконечность простых близнецов.

fish224 Автор
28.10.2023 08:27Вы имели в виду две пары простых чисел-близнецов?

Milliard
28.10.2023 08:27@DieselMachineимел в виду два числа-близнеца, не обязательно из одной пары. https://oeis.org/A007534

Wiggin2014
28.10.2023 08:27+2как можно рассуждать о математике, не зная как пишется слово "параллелепипед"????

fish224 Автор
28.10.2023 08:27Я исправлял ошибки в тексте перед публикацией, но почему-то это исправление не сохранилось

RedMadCat
28.10.2023 08:27Прочитал статью вроде как по математике. В конец вывод - перебор нужно доводить до конца. Ну, приведите примеры доведенных до конца переборов на множестве хотя бы натуральных чисел

Sau
28.10.2023 08:27+3Понятно, что только Чак Норрис может перебрать все натуральные числа. Но вот гипотезу четырёх красок доказывали перебором всех оставшихся вариантов используя компьютер:
"Это была первая крупная проблема в математике, доказательство которой существенно использовало компьютер. На первом шаге авторы, используя логические рассуждения, доказали, что теорема верна для всех карт, если она верна для конкретного конечного набора карт. Набор включал в себя 1936 случая! Для раскраски этого набора карт и был использован компьютер." - цитата из интернета


gwathedhel
Мне, как достаточно далёкому от математики человеку, очень интересно - как возникли такие задачи. И главное, при их доказательстве, что это даст? Какие задачи можно будет решить, доказав (или опровергнув) эти?
garwall
ну может для конкретной задачи и не будет практического применения, но вот методы, разработанные для их решения, в итоге могут сделать очень много - вторая проблема Гильберта дала нам машину Тьюринга, например.
VPryadchenko
почему так важно для вас решить эту задачу?
потому что это просто ох**нно!
Sarjin
красивая сказка. только пример Перельмана показывает что Ваша распиаренная фраза является только распиаренной фразой.
zabanen2
такой вопрос можно задать любому ученому)
ReadOnlySadUser
Вы просто не прониклись сутью математики. Я сам далёк от математиков, но судьба так распорядилась, что на некоторое время в жизни я оказался ими окружён. Волей-неволей погрузился в атмосферу и осознал простую истину.
Трушные математики НЕ РЕШАЮТ НИКАКИХ ПРОБЛЕМ. Они просто упарываются по задачам и чёто там решают просто по причине "а почему бы и нет". Всё. Ничего больше. Просто "по приколу".
Потом уже результаты их упоротости берут прикладные математики и прикладывают куда-нибудь)
niktor_mpt
Как-то внутренне протестую против такого упрощения математиков.
Изначально математика шла по пути обобщения эмпирического опыта, её достижение - формирование идеальных внепредметных объектов, оперирование которыми не требовало специфического предметного опыта, но результаты операций переносились (интерпретировались) на любой предмет. Это известные со школы геометрия и арифметика.
Затем, накопив таких объектов, стали решать задачу уже их унификации и обобщения. Это, например, вещественные и комплексные числа. Эти объекты уже никакой эмпирики в основе не имели. Но потом, конечно, нашли им применение.
Дальше мир идеального вырос настолько, что сам стал предметом эмпирического опыта. И математики, наконец, получили свою башню из слоновой кости. :). Стали изучать свлй собственный мир.
Но мир искусственного не застыл на месте, он постоянно усложняется, поэтому для оперирования им нужны новые идеальные объекты. Теория хаоса, линейное программирование, цепи Маркова и прочая возникли как реакция на проблемы, а не "не вдруг захотелось математику". И их делали настоящие математики первого рода.
А настоящих математиков второго рода - их задача цементировать, структурировать сложившийся хаос идеального мира математических конструктов.
А есть третий тип, который "строгает опилки" - находит какие-то частные случаи, свойства - в общем накапливает математическую эмпирику для тех, кто потом её обощит в один объект. Для второго типа. Это как бы подготовка для поиска философского камня - единое основание математики. Типа того, чем Бурбаки занимались :).
Вы про третий тип?
saboteur_kiev
Во многих случаях тупо никакие.
Математика, в отличие от физики, сильно зависит от собственных условий и нотаций.
Тот же "совершенный кубоид" - ежу понятно, что фигура такая существует, но математическое требование целого натурального числа завязано на нашу нотацию и 10-ричную систему исчисления, поэтому подобрать именно в таких условиях возможно и не выйдет на существующем оборудовании.
Может быть какой-нить математик переберет системы исчисления и "решит" эту задачу, но реального применения она не имеет. Если надо сделать фигуру - просто воспользуйся float..
gaba_m
Прошу прощения, не уловил, как она привязана к системе счисления?
saboteur_kiev
Ну мне вот однажды открыли глаза, пояснив что в 12-ричной системе можно поделить 5 на 3 без "периода".
selivanov_pavel
Нацело 5 поделить на 3 нельзя ни в какой системе счисления. Но, разумеется, для любой дроби системы счисления с кратным знаменателю основанием могут выразить её в записи без периода. Выбранная нотация никак не меняет свойств чисел.
saboteur_kiev
то есть вы согласны, что натуральное целое число - это такая нотация?
selivanov_pavel
Нет, и натуральное, и целое - математические построения, базирующиеся на небольшом количестве аксиом. А запись в какой-то системе счисления - это уже нотация, она ничего не меняет. Можно сделать какую-нибудь систему счисления с иррациональной базой, в ней все целые числа будут представлены в виде бесконечных непериодичных дробей. Но их свойства это никак не поменяет. Нотация - это просто удобный(или неудобный) способ однозначного представления каких-то объектов.
SuperTEHb
Кажется, вы путаете цифры с числами.
tmxx
в такой системе 3/5 будет периодической
paulvl65
Есть более глобальные задачи и теории, решение, которых позволяет лучше понять мироустройство и использовать известные доказанные факты для моделирования. Без решения частных задач, которые перечислены, не решить общие. Задачи эти появились, как это обычно и бывает - исследовались свойства в конкретных областях матанализа или аналитической геометрии и обнаруживались закономерности. Теперь их хотят доказать и обосновать. Примечательно другое, при приписывании ИИ интеллекта и вычислительных мощностей почему то эти задачи решить не могут. :)
samozvet
С такими кривыми формулировками можно себе самому эйнштейна присваивать.
"сумме двух простых чисел" = "количество простых чисел бесконечно"