
Про кубит и про Дирака
Как и бит, кубит допускает два собственных состояния, обозначаемых |0> и |1> (обозначения Дирака), но при этом может находиться и в их суперпозиции.
В общем случае его волновая функция имеет вид A|0>+B|1>, где A и B называются амплитудами вероятностей и являются комплексными числами, удовлетворяющими условию |A|^2+|B|^2=1 (но это не обязательно соблюдать при записи - всегда подразумевается, что происходит нормирование величин).
При измерении состояния кубита можно получить лишь одно из его собственных состояний.
Вероятности получить каждое из них равны соответственно |A|^2 и |B|^2.
Как правило, при измерении состояние кубита необратимо разрушается, чего не происходит при измерении классического бита.
В квантовых вычислениях, мы имеем факт, что применение трансформации Адамара H к кубиту в состоянии |0> даёт нам его в равновероятном состоянии для исходов |0> и |1>, то есть в состоянии |0>+|1>
Но как нам задать нужное состояние кубита, то есть с заранее заданными значениями A и B ?
Вернее, как задать нужное состояние кубита, используя только минимальный набор базовых операций? Ведь любой QDK должен включать в себя методы инициализации кубита (и желательно в требуемом состоянии).
Ну а мы ограничимся в данном примере операциями H и Controlled X.
Как будем решать проблему?
Важнейшее свойство квантовых вычислений - это возможность переводить массивы кубитов в запутанное состояние.
Предположим у нас есть регистр (массив) кубитов, находящийся в состоянии SUM |k> где k=0..N-1 - то есть при попытке измерения мы получим значение из диапазона 0..N-1 с одинаковой вероятностью.
Если мы разделим множество 0..N-1 на два множества A и B то можем сделать функцию f(k)={0, if k in A, и 1, if k in B}. Очеводно, что для произвольно выбранного значения k выполнено P(f(k)==0)=|A|/N и P(f(k)==1)=|B|/N и при этом |A|+|B|=N.
А как проще всего разделить 0..N-1 на два подмножества - конечно пороговой функцией fw(k)={0, if k lt w, и 1, if k ge w} или, в другой записи fw(k)=SIGN(w-k-1), где SIGN(x)={0 if x ge 0, 1 if x lt 0}
При этом p=P(0)=w/N и q=P(1)=(N-w)/N
Рассмотрим классическую схему построения трансформации, для булевой функции fw
Uw(x,y)=(x,y xor fw(x))
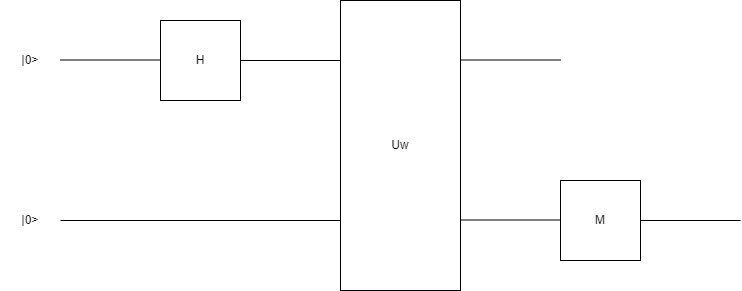
Имеем, что после применения трансформации Uw к регистру в состоянии SUM |k>|0> он перейдёт в состояние SUM |k>|fw(k)>, а при измерении выходного кубита, будет происходить его коллапсирование и измерение вернёт значение |0> с вероятностью p=w/N и |1> с вероятностью q=1-p=(N-w)/N. То есть, если мы в дальнейшем перестанем обращать внимание на значения входных кубитов, то для нас выходной кубит будет просто находиться в состоянии SQRT(p)|0>+SQRT(q)|1>, то есть мы решили задачу - как задать параметры у возможных состояний кубита (мы задали состояние кубита).
Как проверить, что рассуждения корректны?
Ответ - практика. То есть для заданных значений p и q многократно повторим эксперимент задание начального состояния кубита и измерение его значения (коллапсирование). Статистика полученных результатов |0> и |1> должна совпасть с заданными параметрами p и q.
А вот и программка и её результат
namespace qrnd {
open Microsoft.Quantum.Canon;
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Arrays;
open Microsoft.Quantum.Convert;
open Microsoft.Quantum.Math;
open Microsoft.Quantum.Logical;
open Microsoft.Quantum.Diagnostics;
open Microsoft.Quantum.Bitwise;
/// # Описание
/// измерение значений (коллапсирование) кубитов в массиве (который рассматриваем как один регистр)
/// и возврат числа (равного полученной двоичной последовательности)
operation Measure(qubits: Qubit[]) : Int {
let results = ForEach(M, qubits);
let i = ResultArrayAsInt(results);
return i;
}
/// # Описание
/// вычисления знака переноса при арифметической операции сложения
/// то есть трансформация вида |k>|0> -> |k>|sign(k+value)>
operation Sign(target: Qubit[], sign: Qubit, value: Int) : Unit {
let k = Length(target);
let bools = IntAsBoolArray(2^k-value, k);
use (qubits) = (Qubit[2]) {
for idx in 0..k-1 {
let carry = qubits[idx%2];
let next = qubits[1-(idx%2)];
// вычисляем следующее значение флага переноса разряда
if(bools[idx]) {
// next = carry*target[idx]^carry^target[idx]
Controlled X([carry, target[idx]], next);
Controlled X([carry], next);
Controlled X([target[idx]], next);
}
else {
// next = carry*target[idx] = carry&target[idx]
Controlled X([carry, target[idx]], next);
}
Reset(carry);
}
Controlled X([qubits[k%2]], sign);
ResetAll(qubits);
}
}
@EntryPoint()
operation Main(n: Int, w: Int, tests: Int) : Unit {
Message("Hello quantum world!");
let N=2^n;
let p=100*w/N;
let q=100*(N-w)/N;
Message($"n={n} w={w} N={N} p={p}% q={q}% tests={tests}");
mutable counters = [0, size=2];
use (x,y)=(Qubit[n],Qubit()){
for _ in 1..tests {
ApplyToEach(H,x);
Sign(x,y,w);
let res = Measure([y]);
set counters w/= res <- counters[res]+1;
ResetAll(x);
Reset(y);
}
}
let f = [w,N-w];
mutable total = 0;
for element in f {
set total+=element;
}
for idx in 0..1 {
let expect = tests*f[idx]/N;
let fact = counters[idx];
Message($"{idx}: ... expect={expect} ... fact={fact}");
}
}
}
PS C:\Projects\qrnd> dotnet run -n 4 -w 5 --tests 1000
Hello quantum world!
n=4 w=5 N=16 p=31% q=68% tests=1000
0: ... expect=312 ... fact=289
1: ... expect=687 ... fact=711
PS C:\Projects\qrnd> dotnet run -n 4 -w 5 --tests 1000
Hello quantum world!
n=4 w=5 N=16 p=31% q=68% tests=1000
0: ... expect=312 ... fact=275
1: ... expect=687 ... fact=725
PS C:\Projects\qrnd> dotnet run -n 4 -w 5 --tests 1000
Hello quantum world!
n=4 w=5 N=16 p=31% q=68% tests=1000
0: ... expect=312 ... fact=292
1: ... expect=687 ... fact=708
PS C:\Projects\qrnd> dotnet run -n 4 -w 5 --tests 1000
Hello quantum world!
n=4 w=5 N=16 p=31% q=68% tests=1000
0: ... expect=312 ... fact=324
1: ... expect=687 ... fact=676
И задачка со звёздочкой
А давайте рассмотрим трансформацию U(w,x,y)=(w,x,y xor SIGN(w-x-1)) где параметр w так же перебирается с помощью квантовых вычислений, то есть так же описывается суммой возможных состояний (с вероятностями).
Но это, как говорится, уже другая история ... тут и алгоритм Гровера становится более интересным ...
Ссылки
https://learn.microsoft.com/ru-ru/azure/quantum/tutorial-qdk-grovers-search?tabs=tabid-visualstudio
https://learn.microsoft.com/ru-ru/azure/quantum/user-guide/host-programs?tabs=tabid-copilot


dprotopopov Автор
господи, как "войти в ит" за.. (очень нравятся)