
Алгориитм Шора — квантовый алгоритм факторизации (разложения числа на простые множители), позволяющий разложить число M за время O((logM)^3) используя O(log M) логических кубитов.
Алгоритм Шора был разработан Питером Шором в 1994 году. Семь лет спустя, в 2001 году, его работоспособность была продемонстрирована группой специалистов IBM. Число 15 было разложено на множители 3 и 5 при помощи квантового компьютера с 7 кубитами.
Алгоритм Шора состоит из 2-х частей - квантовых и классических вычислений.
Квантовая часть алгоритма отвечает за определение периода функции с помощью квантовых вычислений.
Классические вычисления решают задачу как по найденному периоду степенной функции найти разложение на сомножители.
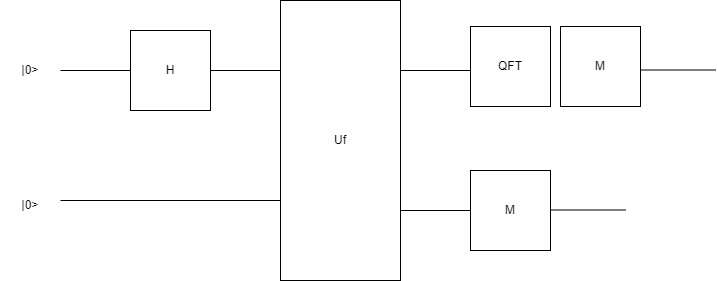
Практически, схема этого алгоритма полностью повторяет схему алгоритма Саймона, с отличием в последнем шаге - вместо применения оператора Адамара перед измерением входного регистра, используется оператор преобразования Фурье.
А какие есть ещё варианты определить период функции используя квантовые вычисления?
Когда-то ранее я писал статьи про способы сравнения (поиска фрагмента) изображений, поиска частоты сердечных сокращений с использованием операции вычисления скалярного произведения, которую я делал с помощью свёртки на основе БФП.
а так же начал повторять эту технологию при квантовых вычислениях
Так почему бы не повторить успешный успех и, заодно, обобщить теорию вопроса?
Начнём ...
Пусть у нас есть функция f: {0,1}^n to {0,1}^m.
Очевидно, что мы можем её так же записать, и как f: {0,1}^n to Z и как f: {0,1}^n to [0,1) без потери общности рассуждений (то есть {0,1}^m можно рассматривать и как двоичное представление целого числа, и как рациональную дробь полученную делением целого числа на 2^m)
Вычисление скалярного произведения через инверсию и свёрку
Пусть у нас есть кольцо с операцией op и пара функций a и b, отображающих кольцо в поле, например комплексных чисел
Операцией свёрки a и b мы будем называть функцию c = a x b, такую что c(i) = SUM a(ix)b(iy)|i=ix op iy
Пусть у нас есть кольцо с операцией op и функция f, отображающих кольцо в поле, например комплексных чисел (но здесь, если вы заметите, я использую только отображение в действительные числа)
Операцией инверсией аргумента назовём функцию inv f , такую что (inv f)(i) = f( -i ), где i op -i == 0
Скалярным произведением a и b называют (a,b) = SUM a(i)b(i) (=(a,b)(0) где (a,b)(i) = SUM a(ix)b(iy)|i=ix-iy)
Легко убедиться самостоятельно, что (a,b) = a x (inv b)
Пусть для регистров кубитов a и b
a = SUM A(i)|i>
b = SUM B(i)|i>
Тогда, если op:
xor: (a,b)(i) = a xor X(b) = SUM A(ix)B(iy)|i>|i=ix xor ~iy
add: (a,b)(i) = a sub b = a add X(b) add |1> = SUM A(ix)B(iy)|i>|i=ix-iy
Что даёт нам вычисление функции-скалярного произведения a и b?
Ответ - если A(i)~=B(i op k) для всех i и распределения отличны от тривиальных, то значение (a,b)(k) является максимальным (по модулю) среди других значений этой функции
А значит, если мы имеем пару регистров кубитов, содержащих частотные характеристики двух последовательностей, то
вычисление свёртки этих двух регистров,
измерение результата,
даст нам наиболее вероятное значение |k>
И, соответственно, если мы работаем с одной функцией, и F(i)~=F(i (op k)^j), то
вычисление свёртки функции самой с собой
измерение результата
с большой вероятностью даст нам значение 0 (op k)^j - то есть один из периодов функции
И как это применить?
Предположим, что мы можем сформировать состояние квантового регистра по правилу SUM SQRT(f(x))|x> (что, собственно, предполагает и алгоритм Шора).
Тогда, применив вышеизложенные рассуждения по свёртке функции f самой с собой, мы получим значения - кандидатуры на период функции f.
Таким образом, мы получили ещё один из вариантов для квантовой части алгоритма Шора - то есть алгоритм поиска периода функции, со своим бэк-джеком и шл... и без использования Фурье-трансформаций.
А как выглядит трансформация для вычисления свёртки?
Да весьма просто - это либо реализация операции арифметического вычитания в кольце 2^n, но реализованная на регистрах из кубитов, либо операция исключающего или над векторами длины n, реализованная на регистрах кубитов.
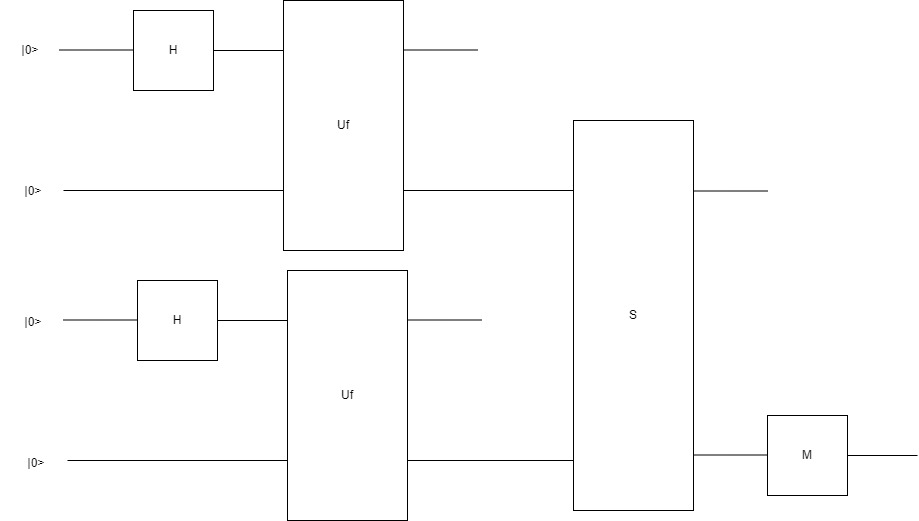
или другой вариант тех же рассуждений
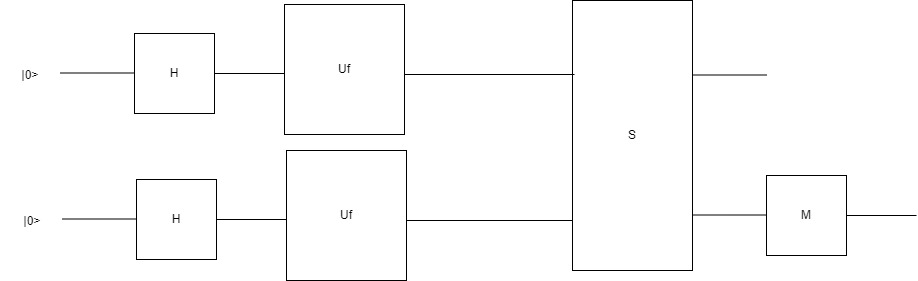
где Uf отвечает за перераспределение вероятностей в соответствии со значениями функции f
В чём квантовое превосходство по сравнению с классическими вычислениями?
Если функция f (или пара функций) задана на множестве мощности N (обычно N=2^n) то при вычислении свёртки "в лоб" требуется O(N^2) операций, но благодаря "быстрым преобразованиям" таким, как БФП, преобразования Адамара и так далее, вычисление свёртки удаётся реализовать за O(NlogN) операций. При этом алгоритм обычно выглядит следующим образом:
Применяем "прямое быстрое преобразование" к функции (паре функций)
Поэлементно умножаем элементы (второй множитель берётся сопряжённым)
Выполняется "обратное быстрое преобразование" от полученного произведения
При использовании квантовых вычислений - вычисление свёртки происходит за один "шаг" то есть за одну не сложную трансформацию.
Вот и всё ...
И бонусом - как реализовать SUM SQRT(f(x))|x>, используя базисные гейты?
Если погуглить, то можно найти разные способы решения этой задачи, например Decomposing unitary matrix into Q# quantum gates.
Но мы не ищем лёгких путей!!!
Например, ранее я писал статью, как задать требуемое состояние в кубите, а эту технику легко адаптировать к нашей задаче - задать состояние регистра кубитов равным значениям исследуемой функции.
И таки да - мы не занимаемся экономией кубитов - в данных рассуждениях потребовалось ещё (m+1)2^n дополнительных кубитов, только для того, чтобы задать коэффициенты с нужным значением вероятности у регистра из n кубитов (но и сам алгорим Шора не отвечает на вопрос как задать требуемое состояние регистра кубитов).
Ссылки
https://learn.microsoft.com/ru-ru/azure/quantum/tutorial-qdk-grovers-search?tabs=tabid-visualstudio
https://learn.microsoft.com/ru-ru/azure/quantum/user-guide/host-programs?tabs=tabid-copilot
Ранее
Комментарии (23)

tumbler
10.11.2023 08:31+1В 2004-м проходили его на курсе квантовой физики. Неужели с тех пор ничего поновее и поинтереснее не придумали?

quverty
10.11.2023 08:31Вычисление свертки за один шаг часто приводят как аргумент в пользу оптических вычислений. Однако, в квантовых вычислениях очень много информации может теряться в процессе измерения состояния регистра, так что там надо и это учитывать, чтобы оставалось какое-то преимущество.

dprotopopov Автор
10.11.2023 08:31повторенье - мать учения
в квантовых вычислениях всё носит вероятностный характер ... ну а в жизни, что имеет вероятность 99.99% мы считаем абсолютной истинной (даже в быту)

quverty
10.11.2023 08:31Откуда 99.99% ? По той же квантовой обработке образов есть разные работы. Можно посмотреть. Вероятности зависят от набора данных и не обязаны быть близкими к единице.

dprotopopov Автор
10.11.2023 08:31https://pikabu.ru/story/kogda_stoit_puskat_2_raketyi_pvo_9032985
Для начала 2 факта, о которых возможно многие не подозревали:
1. Зенитная ракета часто промахивается
И это норма, поэтому у них и стоят осколочные и осколочно стержневые бч, способные и на расстоянии 20м поразить цель.
2. Вероятность поражения цели около 0.6
В принципе вытекает из первого. Да, у ракеты есть промах, а еще (удивительно) цель не хочет чтобы в неё попали, поэтому всячески маневрирует и стреляет ловушками тепловыми.Ну и теперь, когда вы готовы представляю скромную табличку, где на основании имитационной мат. модели, (основанной на 19 дифф. уравнениях и методе Рунге-Кутты 4го порядка с запаздыванием) я собственно и рассматривал разные схемы/тактики пуска.
Сложные слова выше можно не читать, просто обратите внимание на сколько повышается вероятность поражения при пуске двух ракет.
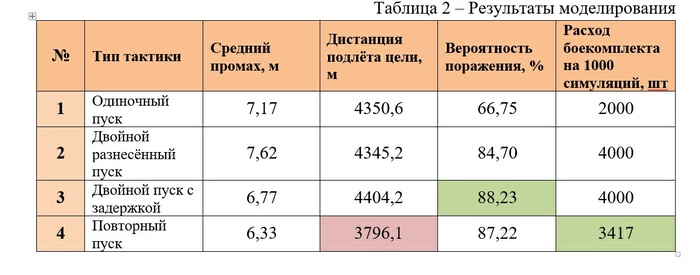
Когда стоит пускать 2 ракеты ПВО? Оружие, Ракета, Наука, Математика, Инженер, Видео, Вертикальное видео Да, многое зависит от самой ракеты и тут весьма специфические данные для специфической ракеты, о которой мы говорить не будем :)

quverty
10.11.2023 08:31+1Темой были квантовые вычисления, а не зенитные ракеты. В квантовых вычислениях из-за линейности квантовой механики формулы достаточно простые - вероятность неудачи возводится в степень количества попыток. Вероятность успеха - единица минус вероятность неудачи. Если она не очень большая, то её приближённо можно просто умножать на количество попыток.

dprotopopov Автор
10.11.2023 08:31Да ... вы сами ответили на свой вопрос

quverty
10.11.2023 08:31-1Нет не ответил. Совершенно непонятно, как вы оцениваете вероятность успеха, чтобы она достигла разумных значений, если в квантовых вычислениях она просто растёт линейно с количеством попыток и при этом может быть достаточно маленькой.

dprotopopov Автор
10.11.2023 08:31Вас никто не заставляет городить вавилонскую башню из кучи последовательных трансформаций, чтобы в итоге получить нулевую вероятность успеха, которую уже многократными попытками не вытянешь ... неужели так трудно делать расчёты "по-шагам"?

quverty
10.11.2023 08:31Вы уже писали о вавилонской башне, но мне не очень понятно что имеется в виду. На всякий случай повторю, что квантовые вычисления линейны и требование учитывать предыдущие шаги по моему опыту может быть действительно трудным. Не могу сказать что невозможным, так что желаю успехов.

AndrChm
10.11.2023 08:31сокращений с использованием операции вычисления скалярного произведения, которую я делал с помощью свёртки на основе БФП.
Что такое БФП? Рискну предположить, что это БПФ, а именно Быстрое Преобразование Фурье. Специалисты используют такой акроним. Иными словами, эффективный способ вычисления дискретного преобразования Фурье (с полиномиальной трудоёмкостью). Будем считать, что это описка. Поясните в противном случае.

dprotopopov Автор
10.11.2023 08:31Быстрое Фурье Преобразование (с точность до перестановки) . по-англицки: Fast Fourier Transfer
И у специалистов оно идёт под FFT

AndrChm
10.11.2023 08:31https://ru.wikipedia.org/wiki/Быстрое_преобразование_Фурье
Вы же пишете по-русски, а не по-английски…
Операцией свёрки a и b мы будем называть функцию c = a x b, такую что c(i) = SUB a(ix)b(iy)|i=ix op iy
А что такое SUB? Наверное SUM? Может лучше в LaTex формулы делать, что бы было как у человеков принято?

AndrChm
10.11.2023 08:31Можно много вопросов задать по-поводу этого текста. Но в какой-то момент начинаешь понимать, что это шутка такая…

dprotopopov Автор
10.11.2023 08:31Ага ... и которая, на удивление, работает, и работает отлично ...

AndrChm
10.11.2023 08:31Ага… И как работает? Где работает? Почему работает? И что значит отлично? Это всё слова. Нет никакого внятного объяснения. Вы вводите какие-то странные обозначения, которые можно по-разному истолковывать. Да и тематика довольно затасканная сама по себе. На мой взгляд, это всё выглядит как очередной «Корчеватель». Возможно над текстом ещё и AI поработал. Уж больно характерные языковые ошибки просматриваются, начиная с грамматики и пунктуации, и заканчивая стилистикой. Более того, публикации такого рода вполне возможны, — ведь на Хабр отсутствует рецензирование.
В общем, всё что тут публикуется надо тщательно фильтровать.




dprotopopov Автор
Думаю пора выпиливаться с хабра ... скучно тут у вас ...
Travisw
хоть бы объяснил что такое период функции и как он находится, математическими значками естественно
dprotopopov Автор
Вроде, как обычно - подразумевается, что f(x+p)=f(x) - так и у Шора.
Естественно на "зацикленность" особо внимания не обращают - то есть полагают 0 < p << 2^n
А для взлома RSA полагают f(x)=a^x mod N для случайного a и после нахождения периода в дело вступает классический алгоритм, который выполнит факторизацию. И вероятность успеха этой цепочки вычислений ~1/2. То есть 10 попыток дадут вероятность угадывания 99.99% - чище чистого золота.
AndrChm
Вы бы хоть что-нибудь почитали про вероятность, что-ли. Например, можно Джозефа Мазура «Игра случая» для начала, вполне популярно и доходчиво. Про слабый закон больших чисел и теорему Бернулли. А то как-то совсем уж…