Базовым элементом построения нейросетей, как мы знаем, является модель нейрона, а, соответственно, простейшей моделью нейрона, является перцептрон.

С математической точки зрения, перцептрон решает задачу разделения пространства признаков гиперплоскостью, на две части. То есть является простейшим линейным классификатором.

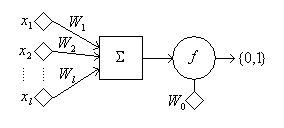
Обобщенная схема нейрона представляет собой функцию f(SUM Wi*xi - W0)

Здесь

• x1,...,xn – компоненты вектора признаков x=(x1,x2,...,xn);

• SUM – сумматор;

• W1,W2,...,Wn – синоптические веса;

• f – функция активации; f(v)= { 0 при v < 0 и 1 при v>0 }

• W0 – порог.

Таким образом, нейрон представляет собой линейный классификатор с дискриминантной функцией g(X)=f(SUM Wi*Xi - W0).

И задача построения линейного классификатора для заданного множества прецедентов (Xk,Yk) сводится к задаче обучения нейрона, т.е. подбора соответствующих весов W1,W2,...,Wn и порога W0.

Классический подход обучения перцептрона хорошо известен

• Инициализируем W0,W1,W2,...Wn (обычно случайными значениями)

• Для обучающей выборки (Xk,Yk) пока для всех значений не будет выполняться f(SUM WiXki - W0)==Yi повторяем последовательно для всех элементов:

• W = W + r(Yk - f(SUM WiXki - W0))Xk, где 0 < r < 1 - коэффициент обучения

Для доказательства сходимости алгоритма применяется теорема Новикова, которая говорит, что если существует разделяющая гиперплоскость, то она может быть найдена указанным алгоритмом.

Что же нам может предложить модель квантовых вычислений для решения задачи обучения перцептрона - то есть для нахождения синоптических весов по заданной обучающей выборке?

Ответ - мы можем сразу опробовать все возможные значения весов и выбрать из них тот - который удовлетворяет нашим требованиям - то есть правильно разделяет обучающую выборку.

Для понимания данного туториала вам потребуются базовые знания по

• нейросетям

• квантовым вычислениям (кубиты и трансформации)

• программированию на Q-sharp

Замутим небольшие рассуждения

Пусть мы имеем обучающую выборку (Xk,Yk), где Xk - двоичный вектор из {0,1}^n, и Yk - тоже является двоичным значением из {0,1} (это условие делается для упрощения задачи, и ни в коей мере не накладывает ограничение на обобщение).

Модель перцептрона, предполагает, что W0,W1,W2,...,Wn являются действительными числами

• но математически легко доказать, что если существует решение в рациональных числах, то существует решение и в целых числах.

• а для конечной обучающей выборки, если существует решение в действительных числах, то будет существовать решение и рациональных числах.

• таким образом мы можем искать нужные нам коэффициенты W0,W1,W2,...,Wn в целых числах

Предположим, также, что значения W0,W1,W2,...,Wn могут быть представлены двоичными числами с не более чем m разрядов (соответственно, старший разряд будет показывать знак целого числа)

Таким образом, у нас получается, что

• можно взять m(n+1) кубитов и рассматривать их как двоичное представление n+1 целого числа W0,W1,W2,...,Wn,

• для обучающей выборки (Xk,Yk) вычислить число несовпадений Error(W) = SUM (sign(SUM Wi Xki - W0) xor Yk), где sign - взятие старшего (знакового) разряда

• найти такой W, что Error(W)=0

И тут мы видим, что последний пункт - это есть условие для применения алгоритма Гровера!!! А для него уже давно и много чего написано.

Алгоритм Гровера представляет собой обобщённый, независящей от конкретной задачи поиск, функция которого представляет "чёрный ящик" f: {0,1}^n to {0,1}^n, для которой известно, что EXISTS!w:f(w)=a, где a - заданное значение (считаем, что для f и заданного a можно построить оракул Uf: { |w> to |1>, |x> to |0> if |x> != |w> })

Алгоритм Гровера достаточно прост

1. Задаём в регистре (массиве кубитов) начальное значение H|0>

2. Повторяем несколько раз (исходя из оценки) пару трансформаций над регистром

• Отражение от решения Uw: { |w> to -|w>, |x> to |x> if |x> !=|w> } или Uw = I-2|w><w|

• Отражение от s=H|0> Us = 2|s><s|-I

3. Забираем нужное решение из регистра (с большой долей вероятности, что оно правильное)

Таким образом, мы свели задачу обучения перцептрона по выборке, к известному алгоритму квантовых вычислений - алгоритму Гровера.

А зачем всё это, здесь же не удалось ускорить расчёты, и их даже стало больше?

Если, вы знакомы с алгоритмом Гровера, то понимаете, что по сравнению с полным перебором, вместо N/M итераций, он требует PI/4*SQRT(N/M) итераций, где N - число всех возможных вариантов перебора, а M - число возможных решений задачи.

В данном случае, N=2^(m(n+1)) и решение задачи потребует оценку O(2^(m(n+1)/2)) итераций в худшем случае, что при больших m и n делает сомнительным выгоду от использования квантовых вычислений.

Отвечу - да, вы правы в своих сомнениях на текущий момент времени. Лично я уверен, что (уже сейчас) существуют более быстрые алгоритмы по сравнению с алгоритмом Гровера - просто общественности может быть о них неизвестно о них на текущий момент времени (вспомним как это было с алгоритмом, известным впоследствии как RSA). А пока, примите данное решение, как один из вариантов обучения перцептрона с помощью квантовых вычислений.

Рон Ривест, Ади Шамир и Леонард Адлеман из Массачусетского технологического института в течение года предприняли несколько попыток создать одностороннюю функцию, которую было бы трудно инвертировать. Ривест и Шамир, будучи компьютерными учеными, предложили множество потенциальных функций, а Адлеман, будучи математиком, отвечал за поиск их слабых мест. Они опробовали множество подходов, включая "ранцевый" и "перестановочные полиномы". Какое-то время они думали, что-то, чего они хотели достичь, невозможно из-за противоречивых требований. В апреле 1977 года они провели Песах в доме одного из студентов и выпили много манишевицкого вина, а затем вернулись к себе домой около полуночи. Ривест, не в силах заснуть, лег на диван с учебником математики и начал думать о своей односторонней функции. Остаток ночи он провел, формализуя свою идею, и к рассвету большая часть статьи была готова. Алгоритм теперь известен как RSA - инициалы их фамилий в том же порядке, что и в их статье.

Клиффорд Кокс, английский математик, работавший в британской разведывательной службе Government Communications Headquarters (GCHQ), описал эквивалентную систему во внутреннем документе в 1973 г. Однако, учитывая относительно дорогие компьютеры, необходимые для ее реализации в то время, она считалась в основном курьезом и, насколько известно, так и не была применена. Однако его открытие было раскрыто только в 1997 году из-за его сверхсильного засекречивания.

А иногда бывает, что сорока блестяшку приносит ...

Так, что кодим ...

Нам потребуется реализация следующих методов

• Метод арифметики над регистром из кубитов

  • увеличение значения на единицу, то есть трансформация Inc:|k> to |k+1>

  • Сложение, то есть трансформация Add:|a>|b> to |a+b>|b>

  • Добавление константы, то есть трансформация: AddiInt:|k>,value to |k+value>

    /// # Описание
    /// увеличение на единицу числового значения в массиве кубитов (рассматриваемых как регистр)
    /// то есть трансформация вида |k> -> |k+1>
    operation Inc(target: Qubit[]) : Unit is Ctl {
        let n = Length(target);
        for idx in 1..n {
            Controlled X(target[0..n-idx-1], target[n-idx]);
        } 
    }

    /// # Описание
    /// увеличение на указанную величину числового значения в массиве кубитов (рассматриваемых как регистр)
    /// то есть трансформация вида |k>|value> -> |k+value>|value>
    operation Add(target: Qubit[], value: Qubit[]) : Unit {
        let n = Length(target);
        use (qubits) = (Qubit[2]) {
            for idx in 0..n-1 {
                let carry = qubits[idx%2];
                let next = qubits[1-(idx%2)];
                // вычисляем следующее значение флага переноса разряда
                // next = carry+target[idx]+value[idx]>=2
                Controlled X([carry, target[idx]], next);
                Controlled X([carry, value[idx]], next);
                Controlled X([target[idx], value[idx]], next);
                Controlled X([carry, target[idx], value[idx]], next);
                // target[idx] = carry^target[idx]^value[idx]
                Controlled X([value[idx]], target[idx]);
                Controlled X([carry], target[idx]);
                Reset(carry);
            } 
            ResetAll(qubits);
        }
    }
    
    /// # Описание
    /// увеличение на указанную величину числового значения в массиве кубитов (рассматриваемых как регистр)
    /// то есть трансформация вида |k> -> |k+value>
    operation AddInt(target: Qubit[], value: Int) : Unit {
        let n = Length(target);
        mutable bools = [false, size=n];
        if(value>0) {
            let tmp = IntAsBoolArray(value, n);
            for i in 0..n-1 {
                set bools w/= i <- tmp[i];
            }
        }
        if(value<0) { 
            // value = ~(-value)+1
            let tmp = IntAsBoolArray(-value, n);
            mutable carry = true;
            for i in 0..n-1 {
                let next = carry and not tmp[i];
                set bools w/= i <- (not tmp[i] and not carry) or (tmp[i] and carry);
                set carry = next;
            } 
        }

        use (qubits) = (Qubit[2]) {
            for idx in 0..n-1 {
                let carry = qubits[idx%2];
                let next = qubits[1-(idx%2)];
                // вычисляем следующее значение флага переноса разряда
                if(bools[idx]) {
                    // next = carry*target[idx]^carry^target[idx] = carry|target[idx]
                    Controlled X([carry, target[idx]], next);
                    Controlled X([carry], next);
                    Controlled X([target[idx]], next);
                }
                else {
                    // next = carry*target[idx] = carry&target[idx]
                    Controlled X([carry, target[idx]], next);
                }
                
                // добавляем текушее значение флага переноса и добавляемого бита
                Controlled X([carry], target[idx]);
                if(bools[idx]) {
                    X(target[idx]);
                }
                Reset(carry);
            } 
            ResetAll(qubits);
        }
    }

• вспомогательные методы

    /// # Описание
    /// вспомогательный метод для копирования значений массива кубитов
    operation Copy(source: Qubit[], target: Qubit[]) : Unit {
        let n = Length(source);
        for i in 0..(n-1) {
            Controlled X([source[i]], target[i]);
        }
    }

     /// # Описание
    /// измерение значений (коллапсирование) кубитов в массиве (который рассматриваем как один регистр)
    operation Measure(qubits: Qubit[]) : Bool[] {
        let results = ForEach(M, qubits);
        return ResultArrayAsBoolArray(results);
    }

    /// # Описание
    /// измерение значений (коллапсирование) кубитов в массиве (который рассматриваем как один регистр)
    operation MeasureWeights(n: Int, m: Int, qubits: Qubit[]) : Int[] {
        let results = ForEach(M, qubits);
        mutable w = [0, size=n+1];
        for i in 0..n {
            let j = ResultArrayAsInt(results[i*m..(i+1)*m-1]);
            if((j&&&(2^(m-1))) == 0) {
                set w w/= i <- j;
            }
            else {
                set w w/= i <- -((j^^^(2^m-1))+1);
            }
        }
        return w;
    }

• Вычисление значения SUM Wi xi - W0 (где Wi - регистр из m кубитов, xi - значение из {0,1}) и оракул для алгоритма Гровера U(W)=SUM (sign(SUM Wi Xki - W0) xor Yk)

    /// # Описание
    /// подсчёт суммы весов для заданного значения аргумента
    operation SumOfWeights(n: Int, m: Int, arg: Bool[], W: Qubit[], target: Qubit[]) : Unit {
        // target = -W0 = ~W0 + 1
        Copy(W[0..m-1], target);
        ApplyToEach(X, target);
        Inc(target);

        for i in 1..n {
            if(arg[i-1]) {
                Add(target, W[i*m..(i+1)*m-1]);
            }
        }
    }

    /// # Описание
    /// подсчёт числа ошибок для заданной выборки
    operation CountErrors(n: Int, m: Int, l: Int, args: Bool[][], values: Bool[], W: Qubit[], target: Qubit[]) : Unit {
        for i in 0..l-1 {
            use (qubits) = (Qubit[m]) {
                SumOfWeights(n, m, args[i], W, qubits);
                if(not values[i]) {
                    X(qubits[m-1]);
                }
                Controlled Inc([qubits[m-1]],target);
                ResetAll(qubits);
            }
        }
    }

    /// # Описание
    /// реализация оракла, необходимого для алгоритма гровера
    /// соответственно, мы считаем, что правильное решение - это то, которое не имеет ошибок
    operation NoErrorOracle(n: Int, m: Int, l: Int, args: Bool[][], values: Bool[], W: Qubit[], target: Qubit) : Unit {
        use (error) = (Qubit[m]) {
            CountErrors(n, m, l, args, values, W, error);
            ApplyToEach(X, error);
            Controlled X(error, target);
            ResetAll(error);
        }
    }

• Методы алгоритма Гровера (взято с https://learn.microsoft.com/ru-ru/azure/quantum/tutorial-qdk-grovers-search?tabs=tabid-visualstudio)

  • Отражение от решения

  • Отражение от H|0>

  • И, собственно, основной цикл алгоритма Гровера

    /// # Описание
    /// шаг для алгоритма гровера
    /// отражение от решения    
    operation ReflectAboutSolution(oracle : (Qubit[], Qubit) => Unit, register : Qubit[]) : Unit {
        use (target)=(Qubit()){
            within {
                X(target);
                H(target);
            }
            apply {
                oracle(register, target);
            }
        }
    }

    /// # Описание
    /// шаг для алгоритма гровера
    /// отражение от H|0>
    operation ReflectAboutUniform(inputQubits : Qubit[]) : Unit {
        within {
            ApplyToEachA(H, inputQubits);
            ApplyToEachA(X, inputQubits);
        }
        apply {
            Controlled Z(Most(inputQubits), Tail(inputQubits));
        }
    }

    /// # Описание
    /// алгоритм гровера
    operation RunGroversSearch(register : Qubit[], oracle : (Qubit[], Qubit) => Unit, iterations : Int) : Unit {
        ApplyToEach(H, register);
        for _ in 1 .. iterations {
            ReflectAboutSolution(oracle, register);
            ReflectAboutUniform(register);
        }
    }

Подготовим тест

• Сгенерируем параметры гиперплоскости и сгенерируем обучающую выборку

   /// # Описание
    /// генерация параметров случайный гиперплоскости
    operation RandomWeights(n: Int, m: Int) : Int[] {
        use (qubits)=(Qubit[m*(n+1)]){
            ApplyToEach(H, qubits);
            let w = MeasureWeights(n, m, qubits);
            ResetAll(qubits);
            return w;
        }
    } 

    /// # Описание
    /// генерация случайных данных, как обучающей последовательности
    operation RandomTrain(n: Int, m: Int, w: Int[], l: Int) : (Bool[][],Bool[]) {
        mutable args = [[false, size=n], size = l];
        mutable values = [false, size = l];
        use qubits = Qubit[n] {
            for idx in 0..l-1 {
                ApplyToEach(H, qubits);
                let arg = Measure(qubits);
                mutable s = -w[0];
                for j in 1..n {
                    if(arg[j-1]) {
                        set s+=w[j];
                    }
                }
                let value = s>=0;
                set args w/= idx <- arg;
                set values w/= idx <- value;
                ResetAll(qubits);
            }
        }
        return (args,values);
    }

        // подготавливаем случайные данные
        mutable rand_w = [0, size=n+1];
        mutable (args,values)=([[false, size=n],size=l],[false,size=l]);
        mutable isAllZero = false;
        mutable isAllOne = false;

        repeat {
            let temp_w = RandomWeights(n, 2);
            let (temp_args,temp_values) = RandomTrain(n, m, temp_w, l);
            set isAllOne = true;
            set isAllZero = true;
            for i in 0..n {
                set rand_w w/= i <- temp_w[i];
            } 
            for i in 0..l-1 {
                set args w/= i <- temp_args[i];
                set values w/= i <- temp_values[i];
                set isAllOne = isAllOne and values[i];
                set isAllZero = isAllZero and not values[i];
            } 
        }
        until (not isAllOne and not isAllZero);

        Message($"n={n} m={m} l={l} m*(n+1)={m*(n+1)} rand_w={rand_w}");
        
        for i in 0..l-1 {
            Message($"TrainData: {args[i]} -> {values[i]}");
        }

        let noErrorOracle = NoErrorOracle(n, m, l, args, values, _, _);

• Проверим правильность работы построенного оракла

        let noErrorOracle = NoErrorOracle(n, m, l, args, values, _, _);

        // проверка правильности работы оракла
        use (qubits, oracle)=(Qubit[m*(n+1)],Qubit()) {
            for i in 0..n {
                AddInt(qubits[i*m..(i+1)*m-1], rand_w[i]); 
            }
            noErrorOracle(qubits, oracle);
            let w = MeasureWeights(n, m, qubits);
            Message($"SelfCheck: {w} ... oracle = {M(oracle)}");
            if(M(oracle)==One){
                Message($"SelfCheck: Success!!! {w}");
            }
            ResetAll(qubits);
            Reset(oracle);
        }

• Запустим алгоритм Гровера

        // применяем алгоритм гровера
        // точное число шагов у алгоритма мы не знаем (знаем только оценку)
        // поэтому запускаем с разными значениями итераций
        // Повторение итераций после groverIterations сопровождается снижением этой вероятности
        // вплоть до практически нулевой вероятности успеха на итерации 2*groverIterations.
        // После этого вероятность снова возрастает до итерации 3*groverIterations и т. д.
        // В практических приложениях обычно неизвестно, сколько решений имеет ваша задача, 
        // прежде чем вы решите ее. Эффективной стратегией для решения этой проблемы является 
        // "предположение" количества решений путем постепенного увеличения степени двойки (т. е. 1,2,4,8,...).
        // Одно из этих предположений будет достаточно близким для того, чтобы алгоритм нашел решение
        // со средним числом итераций около SQRT(2^n/S) 

        mutable currenIterations = 1;
        set isSuccess = false;
        repeat{
            let repeatTests = 3;
            mutable currentTest = 0;
            repeat {
                set currentTest += 1;
                use (qubits, oracle) = (Qubit[m*(n+1)], Qubit()){
                    RunGroversSearch(qubits, noErrorOracle, currenIterations);
                    noErrorOracle(qubits, oracle);
                    let w = MeasureWeights(n, m, qubits);
                    Message($"GroversSearch: iterations = {currenIterations} ... {w} ... oracle = {M(oracle)}");
                    if(M(oracle)==One){
                        set isSuccess = true;
                        Message($"GroversSearch: Success!!! {w}");
                    }
                    ResetAll(qubits);
                    Reset(oracle);
                }
            }
            until(currentTest>=repeatTests or isSuccess);
            set currenIterations *= 2;
        }
        until (isSuccess);

Полный текст кода

namespace qperceptron {

    open Microsoft.Quantum.Canon;
    open Microsoft.Quantum.Intrinsic;
    open Microsoft.Quantum.Arrays;
    open Microsoft.Quantum.Convert;
    open Microsoft.Quantum.Math;
    open Microsoft.Quantum.Logical;
    open Microsoft.Quantum.Diagnostics;
    
    /// # Описание
    /// увеличение на единицу числового значения в массиве кубитов (рассматриваемых как регистр)
    /// то есть трансформация вида |k> -> |k+1>
    operation Inc(target: Qubit[]) : Unit is Ctl {
        let n = Length(target);
        for idx in 1..n {
            Controlled X(target[0..n-idx-1], target[n-idx]);
        } 
    }

    /// # Описание
    /// увеличение на указанную величину числового значения в массиве кубитов (рассматриваемых как регистр)
    /// то есть трансформация вида |k>|value> -> |k+value>|value>
    operation Add(target: Qubit[], value: Qubit[]) : Unit {
        let n = Length(target);
        use (qubits) = (Qubit[2]) {
            for idx in 0..n-1 {
                let carry = qubits[idx%2];
                let next = qubits[1-(idx%2)];
                // вычисляем следующее значение флага переноса разряда
                // next = carry+target[idx]+value[idx]>=2
                Controlled X([carry, target[idx]], next);
                Controlled X([carry, value[idx]], next);
                Controlled X([target[idx], value[idx]], next);
                Controlled X([carry, target[idx], value[idx]], next);
                // target[idx] = carry^target[idx]^value[idx]
                Controlled X([value[idx]], target[idx]);
                Controlled X([carry], target[idx]);
                Reset(carry);
            } 
            ResetAll(qubits);
        }
    }
    
    /// # Описание
    /// увеличение на указанную величину числового значения в массиве кубитов (рассматриваемых как регистр)
    /// то есть трансформация вида |k> -> |k+value>
    operation AddInt(target: Qubit[], value: Int) : Unit {
        let n = Length(target);
        mutable bools = [false, size=n];
        if(value>0) {
            let tmp = IntAsBoolArray(value, n);
            for i in 0..n-1 {
                set bools w/= i <- tmp[i];
            }
        }
        if(value<0) { 
            // value = ~(-value)+1
            let tmp = IntAsBoolArray(-value, n);
            mutable carry = true;
            for i in 0..n-1 {
                let next = carry and not tmp[i];
                set bools w/= i <- (not tmp[i] and not carry) or (tmp[i] and carry);
                set carry = next;
            } 
        }

        use (qubits) = (Qubit[2]) {
            for idx in 0..n-1 {
                let carry = qubits[idx%2];
                let next = qubits[1-(idx%2)];
                // вычисляем следующее значение флага переноса разряда
                if(bools[idx]) {
                    // next = carry*target[idx]^carry^target[idx] = carry|target[idx]
                    Controlled X([carry, target[idx]], next);
                    Controlled X([carry], next);
                    Controlled X([target[idx]], next);
                }
                else {
                    // next = carry*target[idx] = carry&target[idx]
                    Controlled X([carry, target[idx]], next);
                }
                
                // добавляем текушее значение флага переноса и добавляемого бита
                Controlled X([carry], target[idx]);
                if(bools[idx]) {
                    X(target[idx]);
                }
                Reset(carry);
            } 
            ResetAll(qubits);
        }
    }

    /// # Описание
    /// вспомогательный метод для копирования значений массива кубитов
    operation Copy(source: Qubit[], target: Qubit[]) : Unit {
        let n = Length(source);
        for i in 0..(n-1) {
            Controlled X([source[i]], target[i]);
        }
    }

     /// # Описание
    /// измерение значений (коллапсирование) кубитов в массиве (который рассматриваем как один регистр)
    operation Measure(qubits: Qubit[]) : Bool[] {
        let results = ForEach(M, qubits);
        return ResultArrayAsBoolArray(results);
    }

    /// # Описание
    /// измерение значений (коллапсирование) кубитов в массиве (который рассматриваем как один регистр)
    operation MeasureWeights(n: Int, m: Int, qubits: Qubit[]) : Int[] {
        let results = ForEach(M, qubits);
        mutable w = [0, size=n+1];
        for i in 0..n {
            let j = ResultArrayAsInt(results[i*m..(i+1)*m-1]);
            if((j&&&(2^(m-1))) == 0) {
                set w w/= i <- j;
            }
            else {
                set w w/= i <- -((j^^^(2^m-1))+1);
            }
        }
        return w;
    }

    /// # Описание
    /// подсчёт суммы весов для заданного значения аргумента
    operation SumOfWeights(n: Int, m: Int, arg: Bool[], W: Qubit[], target: Qubit[]) : Unit {
        // target = -W0 = ~W0 + 1
        Copy(W[0..m-1], target);
        ApplyToEach(X, target);
        Inc(target);

        for i in 1..n {
            if(arg[i-1]) {
                Add(target, W[i*m..(i+1)*m-1]);
            }
        }
    }

    /// # Описание
    /// подсчёт числа ошибок для заданной выборки
    operation CountErrors(n: Int, m: Int, l: Int, args: Bool[][], values: Bool[], W: Qubit[], target: Qubit[]) : Unit {
        for i in 0..l-1 {
            use (qubits) = (Qubit[m]) {
                SumOfWeights(n, m, args[i], W, qubits);
                if(not values[i]) {
                    X(qubits[m-1]);
                }
                Controlled Inc([qubits[m-1]],target);
                ResetAll(qubits);
            }
        }
    }

    /// # Описание
    /// реализация оракла, необходимого для алгоритма гровера
    /// соответственно, мы считаем, что правильное решение - это то, которое не имеет ошибок
    operation NoErrorOracle(n: Int, m: Int, l: Int, args: Bool[][], values: Bool[], W: Qubit[], target: Qubit) : Unit {
        use (error) = (Qubit[m]) {
            CountErrors(n, m, l, args, values, W, error);
            ApplyToEach(X, error);
            Controlled X(error, target);
            ResetAll(error);
        }
    }

    /// # Описание
    /// шаг для алгоритма гровера
    /// отражение от решения    
    operation ReflectAboutSolution(oracle : (Qubit[], Qubit) => Unit, register : Qubit[]) : Unit {
        use (target)=(Qubit()){
            within {
                X(target);
                H(target);
            }
            apply {
                oracle(register, target);
            }
        }
    }

    /// # Описание
    /// шаг для алгоритма гровера
    /// отражение от H|0>
    operation ReflectAboutUniform(inputQubits : Qubit[]) : Unit {
        within {
            ApplyToEachA(H, inputQubits);
            ApplyToEachA(X, inputQubits);
        }
        apply {
            Controlled Z(Most(inputQubits), Tail(inputQubits));
        }
    }

    /// # Описание
    /// алгоритм гровера
    operation RunGroversSearch(register : Qubit[], oracle : (Qubit[], Qubit) => Unit, iterations : Int) : Unit {
        ApplyToEach(H, register);
        for _ in 1 .. iterations {
            ReflectAboutSolution(oracle, register);
            ReflectAboutUniform(register);
        }
    }

    
    /// # Описание
    /// генерация параметров случайный гиперплоскости
    operation RandomWeights(n: Int, m: Int) : Int[] {
        use (qubits)=(Qubit[m*(n+1)]){
            ApplyToEach(H, qubits);
            let w = MeasureWeights(n, m, qubits);
            ResetAll(qubits);
            return w;
        }
    } 

    /// # Описание
    /// генерация случайных данных, как обучающей последовательности
    operation RandomTrain(n: Int, m: Int, w: Int[], l: Int) : (Bool[][],Bool[]) {
        mutable args = [[false, size=n], size = l];
        mutable values = [false, size = l];
        use qubits = Qubit[n] {
            for idx in 0..l-1 {
                ApplyToEach(H, qubits);
                let arg = Measure(qubits);
                mutable s = -w[0];
                for j in 1..n {
                    if(arg[j-1]) {
                        set s+=w[j];
                    }
                }
                let value = s>=0;
                set args w/= idx <- arg;
                set values w/= idx <- value;
                ResetAll(qubits);
            }
        }
        return (args,values);
    }

    @EntryPoint()
    operation Main(n: Int, m: Int, l: Int) : Unit {
        Message("Hello quantum world!");

        // подготавливаем случайные данные
        mutable rand_w = [0, size=n+1];
        mutable (args,values)=([[false, size=n],size=l],[false,size=l]);
        mutable isAllZero = false;
        mutable isAllOne = false;

        repeat {
            let temp_w = RandomWeights(n, 2);
            let (temp_args,temp_values) = RandomTrain(n, m, temp_w, l);
            set isAllOne = true;
            set isAllZero = true;
            for i in 0..n {
                set rand_w w/= i <- temp_w[i];
            } 
            for i in 0..l-1 {
                set args w/= i <- temp_args[i];
                set values w/= i <- temp_values[i];
                set isAllOne = isAllOne and values[i];
                set isAllZero = isAllZero and not values[i];
            } 
        }
        until (not isAllOne and not isAllZero);

        Message($"n={n} m={m} l={l} m*(n+1)={m*(n+1)} rand_w={rand_w}");
        
        for i in 0..l-1 {
            Message($"TrainData: {args[i]} -> {values[i]}");
        }

        let noErrorOracle = NoErrorOracle(n, m, l, args, values, _, _);

        // проверка правильности работы оракла
        use (qubits, oracle)=(Qubit[m*(n+1)],Qubit()) {
            for i in 0..n {
                AddInt(qubits[i*m..(i+1)*m-1], rand_w[i]); 
            }
            noErrorOracle(qubits, oracle);
            let w = MeasureWeights(n, m, qubits);
            Message($"SelfCheck: {w} ... oracle = {M(oracle)}");
            if(M(oracle)==One){
                Message($"SelfCheck: Success!!! {w}");
            }
            ResetAll(qubits);
            Reset(oracle);
        }

        let groverIterations = Round(PI()/4.0*Sqrt(IntAsDouble(2^(m*(n+1)))));
        Message($"GroversSearch: groverIterations = {groverIterations}?");

        mutable isSuccess = false;

        // применяем алгоритм гровера
        // точное число шагов у алгоритма мы не знаем (знаем только оценку)
        // поэтому запускаем с разными значениями итераций
        // Повторение итераций после groverIterations сопровождается снижением этой вероятности
        // вплоть до практически нулевой вероятности успеха на итерации 2*groverIterations.
        // После этого вероятность снова возрастает до итерации 3*groverIterations и т. д.
        // В практических приложениях обычно неизвестно, сколько решений имеет ваша задача, 
        // прежде чем вы решите ее. Эффективной стратегией для решения этой проблемы является 
        // "предположение" количества решений путем постепенного увеличения степени двойки (т. е. 1,2,4,8,...).
        // Одно из этих предположений будет достаточно близким для того, чтобы алгоритм нашел решение
        // со средним числом итераций около SQRT(2^n/S) 

        mutable currenIterations = 1;
        set isSuccess = false;
        repeat{
            let repeatTests = 3;
            mutable currentTest = 0;
            repeat {
                set currentTest += 1;
                use (qubits, oracle) = (Qubit[m*(n+1)], Qubit()){
                    RunGroversSearch(qubits, noErrorOracle, currenIterations);
                    noErrorOracle(qubits, oracle);
                    let w = MeasureWeights(n, m, qubits);
                    Message($"GroversSearch: iterations = {currenIterations} ... {w} ... oracle = {M(oracle)}");
                    if(M(oracle)==One){
                        set isSuccess = true;
                        Message($"GroversSearch: Success!!! {w}");
                    }
                    ResetAll(qubits);
                    Reset(oracle);
                }
            }
            until(currentTest>=repeatTests or isSuccess);
            set currenIterations *= 2;
        }
        until (isSuccess);
    }
}

И потестим ...

PS C:\Projects\qperceptron> dotnet run -n 3 -m 3 -l 5 
Hello quantum world!
n=3 m=3 l=5 m*(n+1)=12 rand_w=[0,1,-1,0]
TrainData: [False,True,False] -> False
TrainData: [False,True,True] -> False
TrainData: [False,False,True] -> True
TrainData: [False,False,True] -> True
TrainData: [True,False,True] -> True
SelfCheck: [0,1,-1,0] ... oracle = One
SelfCheck: Success!!! [0,1,-1,0]
GroversSearch: groverIterations = 50?
GroversSearch: iterations = 1 ... [2,-2,0,-3] ... oracle = Zero
GroversSearch: iterations = 1 ... [-2,-4,-2,-1] ... oracle = Zero
GroversSearch: iterations = 1 ... [2,-4,-3,-3] ... oracle = Zero
GroversSearch: iterations = 2 ... [3,1,1,-1] ... oracle = Zero
GroversSearch: iterations = 2 ... [-2,3,-1,-3] ... oracle = Zero
GroversSearch: iterations = 2 ... [3,-1,-3,3] ... oracle = Zero
GroversSearch: iterations = 4 ... [-1,-1,-1,1] ... oracle = Zero
GroversSearch: iterations = 4 ... [3,-3,2,-1] ... oracle = Zero
GroversSearch: iterations = 4 ... [2,2,1,-1] ... oracle = Zero
GroversSearch: iterations = 8 ... [-1,0,3,2] ... oracle = One
GroversSearch: Success!!! [-1,0,3,2]

— Ваше Сиятельство, может мы английскую машинку опробуем?
— А, ну что же, не зря же вы её покупали... Да и случай подходящий.
— Новенькая! Тут, Ваше Сиятельство, человек вроде бы и не нужен, а нужен только его пальчик!
— Да. В смысле техники нам, конечно, до них далеко.
— Так, Афонька... Ты у неё будешь первый. Вещь хорошая, останешься довольный!

Ссылки

• https://github.com/dprotopopov/qperceptron

• Теорема Новикова

• Линейный классификатор

• https://ru.wikipedia.org/wiki/Перцептрон

• https://ru.wikipedia.org/wiki/Алгоритм_Гровера

• https://learn.microsoft.com/ru-ru/azure/quantum/tutorial-qdk-grovers-search?tabs=tabid-visualstudio

• https://learn.microsoft.com/ru-ru/azure/quantum/user-guide/host-programs?tabs=tabid-copilot

• https://learn.microsoft.com/ru-ru/training/modules/qsharp-create-first-quantum-development-kit/2-install-quantum-development-kit-code

• https://ru.wikipedia.org/wiki/RSA

Ранее

• Изучаем Q#. Статистическое сравнение двух последовательностей чисел

• Изучаем Q#. Алгоритм Гровера. Не будите спящего Цезаря

• Изучаем Q#. Делаем реализацию биноминального распределения

• Первые шаги в Q#. Алгоритм Дойча