Как трудно быть абитуриентом мех-мат МГУ / forpes.ru

Главная
Как трудно быть абитуриентом мех-мат МГУ

Как трудно быть абитуриентом мех-мат МГУ +5

10.11.2023 04:30

alexlyk314 11 8800 Источник

Авторы делятся своими воспоминаниями о поступлении и учебе на механико — математическом факультете МГУ. На всякий случай: Ильичев Виталий — окончил кафедру «Математической логики и теории алгоритмов», доктор технических наук, Южный Научный Центр РАН; Маринин Андрей — окончил кафедру «Дифференциальных уравнений», преподаватель Нижегородского госуниверситета.

Эти реальные события произошли много лет тому назад, кажется, в 1967 году. В этот раз на первом экзамене — по письменной математике — предлагались четыре задачи. С точки зрения психологии не совсем ясно какой стратегии на данном экзамене лучше придерживаться. Так, первая «параллельная» стратегия заключается в беглом просмотре всех задач, чтобы примерно оценить их трудность, а затем уже приступить к аккуратному изложению решений. Хорошо, если быстро удается убедиться, что все задачи «вполне решаемы». Это вдохновляет, и позволяет быстро оформить работу. Разумеется, это рискованная стратегия, поскольку можно потратить много времени на поиске решения одной из трудных задач. И тогда не хватит времени на аккуратное оформление остальных. Вторая стратегия — последовательное решении предлагаемых задач. Если решить какую‑то задачу сразу не получается, то переходим к следующей. Это осторожный, но и тревожный путь, который сопровождается чувством неуверенности «в завтрашнем дне».

Какая из этих стратегий «более правильная»? Разумеется, это зависит от индивидуальных качеств абитуриента, связанных с особенностями его нервной системы.

Теперь обсудим задачи первого экзамена. Оказалось, что первые две достаточно стандартные и легко решаемые. В третьей задаче была дана система уравнений с параметром, и требовалось найти его значения, при которых данная система имела единственное решение. Для абитуриентов, имеющих опыт решения олимпиадных задач, она была вполне преодолима и многие с ней справились. А вот в четвертой задаче нужно было найти объем некоего трехмерного тела. С этой справились единицы. Так, что любители рискованных стратегий решения оказалось в сложном положении: мало того, что они не смогли решить задачу 4, но и толком не успели оформить решение задачи 3.

Отметим, что один наш знакомый старшекурсник (Ф. Сурков) заметил, что последняя геометрическая задача легко решается, если знать формулу площади сферического треугольника^[1].

Оформим его информацию в форме следующей задачи.

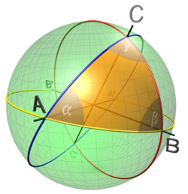
Задача 1. Пусть имеется сфера радиуса , на ее поверхности нарисованы (см. рис. 1) три окружности большого круга. Они образуют криволинейный треугольник (см. рис.1) с углами $\alpha, \beta, \gamma$ . Покажите, что его площадьравняется

$S = \alpha + \beta + \gamma - \pi \;\;\;\;\;\;\; (1)$

«Отчаянные» читатели могут самостоятельно попробовать ее решить. А остальные — проверить на следующем «вкусном» примере. Так, разрежем горизонтально арбуз по экватору, а затем каждую половинку разрежем вертикально на 4 равные части. Теперь вся поверхность арбуза (площади $4\pi$ ) разбивается на 8 равных сферических треугольников. Отсюда находим площадь каждого треугольника, она равна $4\pi /8 = \pi/2$ .

А с другой стороны, здесь всякий треугольник имеет углы $\alpha=\beta=\gamma=\pi/2$ , и тогда согласно (1) получаем $S = \pi / 2$ . Очевидно, этот результат совпадает с предыдущим. Здорово!

Разумеется, предлагать такого сорта задачи на вступительных экзаменах недопустимо. Члены приемной комиссии видимо «осознали» свою вину, и пытались ее компенсировать на другом экзамене — по русскому языку и литературе. Там была предложена следующая загадочная тема сочинения — «Солнце». Здесь допускалась полная вольница (но не менее 3 страниц): Человек — Солнце; Солнце, как астрономический объект, и т. д..

Любопытно, а если бы на страницах сочинения абитуриент изложил решение задачи 4 для сферической поверхности планеты Солнце, то это тоже считалось бы вполне допустимым?

Рис. 1. Сферический треугольник с углами (взято из Википедии – Интернет).

Устный экзамен принимал совсем молодой профессор (будущий академик) Владимир Игоревич Арнольд^[2]. Сам экзаменатор был в прошлом успешный олимпиадник, и рассматривал задачи приемных экзаменов, как некоторую не очень серьезную забаву. По‑сути он превратил экзамен в «сеанс одновременной игры». Так, сразу несколько абитуриентов решали его задачи, а он перемещался от одного к другому. При этом порядок предлагаемых задач был строго дозирован: сначала предлагалась достаточно простая задача, а потом сложность новых задач последовательно увеличивалась. Атмосфера на экзамене была вполне доброжелательной.

Но вот один из абитуриентов захотел показать свои «незаурядные» математические способности, и сообщил профессору (по секрету) не только решение своей задачи, но и решения некоторых задач своих соседей. Эта «демонстрация силы» не очень понравилась В. Арнольду, и тогда он предложил «выскочке» следующую ниже задачу.

Задача 2. Внутри круга радиуса задана некоторая точка . Если через нее провести две взаимно перпендикулярные хорды (см. рис. 2b), то образуются четыре фрагмента — . Требуется найти расположение хорд, при котором сумма квадратов $\sum = AX^2 + AY^2 + AZ^2 + AT^2$ будет максимальной.

Сразу ясно, что устно ее не решить и, вероятно, нужно прибегнуть к тяжелой артиллерии — тригонометрии: составить уравнения длин указанных отрезков в зависимости от угла $(\phi)$ расположения хорд к окружности. Затем определить максимум функции $\sum(\phi)$ путем ее дифференцирования. Это прямолинейный, долгий и скучный подход.

С эстетической точки зрения желательно минимизировать использование тригонометрии^[3].

Великие античные математики (Евклид, Архимед, Пифагор и др.) не знали синусов! Разумеется, здесь надо чувствовать меру. Так теорему о том, что сумма двух сторон ( и ) в невырожденном треугольнике всегда больше третьей () доказать элементарными методами не так‑то просто. Зато привлечение тригонометрии сразу дает решение: пусть $\phi$ — угол между сторонами и , тогда $c^2=a^2+b^2-2 \times a \times b \times \cos(\phi)$ . Отсюда легко получаем .

К счастью, В. Арнольд заметил эти тригонометрические «муки» и будучи удовлетворен своим педагогическим уроком (абитуриент: не буди лихо, пока оно тихо!). Расщедрился и поставил ему досрочно пятерку, и с Богом отправил домой. Кажется, всякий честный абитуриент, вернувшись домой, должен был бы сразу заняться решением этой задачи. Однако, психотравма, нанесенная приключениями на экзамене полностью отбила охоту даже смотреть на нее. Время от времени угрызения совести все‑таки заставляли немного задумываться об этой задаче даже в студенческие годы. Приходили в голову разные частные случаи расположения точки. Например, еслисовпадает с центром круга, тогда естественно для любых взаимно перпендикулярных хорд устанавливаем $\sum=4R^2.$

Чуть менее тривиальным является вариант, когда точканаходится на окружности. В этой ситуации два фрагмента хорд исчезают, а оставшиеся, скажеми, вместе с диаметромобразуют прямоугольный треугольник. Отсюда с помощью Пифагора получаем $\sum = AX^2+AY^2=XY^2=4R^2$ .

Удивительное совпадение! После этого уже будучи зрелым “выскочка” обратился к своему приятелю, который ранее преподавал в математическом лицее. И тот быстро во всем разобрался.

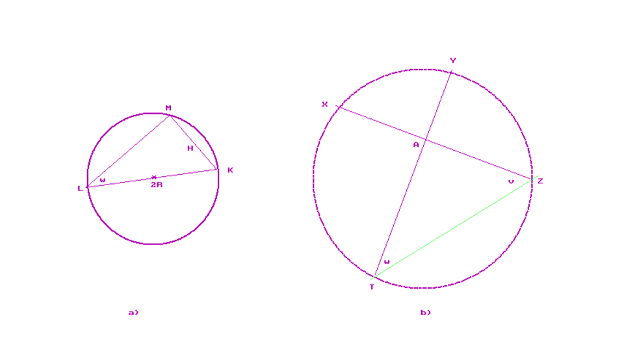
Приводим его короткое решение с совсем малой тригонометрической начинкой (рис. 2)

Сначала напомним, что из любой точки окружности фиксированная хорда выглядит под одним и том же углом. Пусть заданы диаметр окружности ( $KL = 2 \times R$ ) и угол
(), тогда согласно рис. 2a хорда является катетом в прямоугольном треугольникеи ее длина вычисляется по формуле $H=2 \times R \times \sin(w)$ .

Далее, на рис. 2b в треугольнике обозначим углы и
Очевидно, $w+v=\pi/2.$ Согласно напоминанию имеют место соотношения: $YZ=2 \times R \times sin(w)$ и $TX= 2 \times R \times sin(v).$ Поэтому получаем

$YZ^2+TX^2=4 \times R^2. \;\;\;\;\;\;\; (2)$

Аналогично устанавливаем

$XY^2+ZT^2=4 \times R^2 \;\;\;\;\;\;\; (3)$

Из (2) и (3) следует: сумма квадратов всех сторон окамляющего четырехугольника на рис. 2b равна $8 \times R^2.$ Осталось заметить, что $\sum = 2 \times (AX^2+AY^2+AZ^2+AT^2).$ Поэтому окончательно находим

$\sum = 4 \times R^2.$

Действительно, ответ коварный, поскольку не зависит от расположения хорд!

На втором курсе В. Арнольд читал лекции по курсу «Дифференцальные уравнения» целому потоку (=6 групп). Обычно этот предмет рассматривают как разновидность математического анализа с большим количеством формул. Однако в этот раз изложение данной теории было построено на совсем других принципах. Теперь ключевое значение имели следующие понятия: потоки, каскады, векторные поля, фазовые портреты и др. [ 2]. По‑сути, предмет превратился в раздел наглядной геометрии^[4].

Рис. 2. Связка хорды и диаметра через угол между ними – a); 4 фрагмента двух взаимно перпендикулярных хорд XZ и YT – b).

В первом ряду, как правило, располагаются довольно тщеславные студенты, которые хотят показать, что они хорошие ученики — все понимают слету (и поэтому постоянно кивают головами). Это не ускользнуло от внимания ироничного Арнольда, и он решил проучить новоявленных «выскочек». Сделал это он следующим коварным образом. Так, на очередной лекции в первой половине он доказал некую теорему, и перед перерывом спросил аудиторию: «Всем все понятно?» Разумеется, «выскочки» дружно ответили: «Да, конечно», и послушно закивали головами. Тогда В. Арнольд сказал: «А теперь, в перерыве найдите ошибку в моем рассуждении». Повисло тягостное молчание, ну, как в финальной сцене «Ревизора» (Н.В. Гоголь).

Приведем еще один «международный» пример этической аккуратности Арнольда, который он описал в своем учебнике [3]: «Р. Том, которого я обучил этой теории (Андронов. Теории бифуркаций) в 1965 году, стал широко пропагандировать ее под названием бифуркация Э. Хопфа».

Интересной, но и несколько спорной является оценка В. Арнольда недавнего математического прошлого. Так, он пишет [4]: «…двухсотлетие от Ньютона до Римана и Пуанкаре представляется мне математической пустыней, заполненной одними лишь вычислениями.»

Литература

Тихомиров В.М. К восьмидесятилетию Владимира Игоревича Арнольда//Квант, 2017, N 7, C. 2-3.
Арнольд В. И. Обыкновенные дифференциальные уравнения. М.: Наука, 1984. 271 с.
Арнольд В. И. Дополнительные главы теории обыкновенных дифференциальных уравнений. М.: Наука, 1978. 304 с.
Арнольд В.И. Второй закон Кеплера и топология абелевых интегралов// Квант, 1987, N 12, C. 17-24.

[1] Ранее после одной из всероссийских олимпиад академик А.Н. Колмогоров рассказал как можно получить эту формулу.

[2] Еще будучи студентом 3 курса он решил (совместно сА.Н. Колмогоровым) 13 проблему Гильберта о возможности представдения непрерывной функции, как суперпозиции непрерывных функции от двух переменных. Лауреат Ленинской и Государственных премий, а также ряда международных премий [1].

[3] Один известный политик сказал по этому поводу: “Наложить вето на табу”.

[4] Эмоциональный студент из Одессы признавался, что на лекциях В. Арнольда ему иногда хочется петь. Ну, типа: “Я вам советую беречь свои портреты. (Фазовые портреты) ”.

Авторы статьи: В. Ильичев, А. Маринин
Статья подготовлена при поддержке ШАД Хелпер

Комментарии (11)

SlFed
10.11.2023 06:46
#26143748
Не только на мехмате МГУ и не только на экзамене по математике бывают интересные задачи.

Вот какая задача на вступительном экзамене в МЭИ по физике была у меня :

На столе лежит шестигранный карандаш. Какой должен быть коэффициент трения, чтобы когда карандаш толкнули, он скользил по столу, а не катился ?

Для решения достаточно знания школьной физики и геометрии.
1. SuperTEHb
  10.11.2023 06:46
  #26143788
  Аж в голове сразу взорвалась вся элегантная красота этой задачи. Центр тяжести, площадь опоры, везде правильные треугольники... Как раз в школе такими часто баловались.
  1. SlFed
    10.11.2023 06:46
    #26143828
    Браво ! Только площадь опоры тут не нужна, а нужно правило рычага и правильно расписать все силы.
    
    SuperTEHb
    10.11.2023 06:46
    #26143842
    Да, действительно. Всё таки задача рассматривается в сечении, то уже как минимум "отрезок опоры", если можно так сказать. Да и от него лишь одна точка как граничный случай.
    
    SlFed
    10.11.2023 06:46
    #26143862
    Совершенно верно, граничный случай когда весь вес приходится на самый край грани карандаша (сила реакции опоры приложена к ребру).

GospodinKolhoznik
10.11.2023 06:46
#26143834
Площадь дольки, образованной углом альфа равна 2*R^2*альфа. Долька разбивается на 2 "треугольника" - искомый, и дополнительный к нему. Вся сфера полностью покрывается 8 "треугольниками", 2 из которых - искомый и ещё 3 пары дополнения к нему. Дальше путем нехитрых арифметических вычислений доказываем требуемую формулу.

Emelian
10.11.2023 06:46
#26145986
+1
> Как трудно быть абитуриентом мех-мат МГУ

Да не трудно, вовсе! Поступить на математику мехмата МГУ было несложно, куда сложнее было удержаться там.

Я учился на математика в Московском университете с 1985 по 1990 годы. Главное, не требовалось абсолютно ничего за пределами школьной программы. Скажем, на устном экзамене по математике меня попросили доказать теорему синусов. Я говорю, докажу, без проблем, только в программе вступительных экзаменов этого не требуется, только формулировка. Мне поставили пятерку без доказательства и даже без формулировки. Устный по физике тоже прошел без проблем, только перед этим ночь не спал, а до самого экзамена нас допустили лишь в пять вечера, что немного напрягло, хотя в то время я был достаточно стрессоустойчивым.

С письменными было хуже. Сочинение написал быстро, потом несколько раз проверял его и на четвертой проверке правильные слова почему-то исправил на неправильные. Короче, переусердствовал. По письменной математике долго не мог понять условие первой задачи. Скорее всего, что-то там было не вполне корректно сформулировано. Зря только потратил время, надо было решать сначала остальные задачи.

В итоге, две пятерки и две тройки – 16 балов. Проходными для меня были – 14 балов (я шел с трудовым стажем). Для всех остальных – 15 балов. Конкурс был 1.1 человека на место.

В итоге, во главу угла выходит психологическая подготовка, а потом уже математическая. Один парень из Казахстана имел 15 балов, ему сказали, что если получил тройку, то не примут. Он психнул, забрал документы, и уехал, не дождавшись результатов приема. А потом никто не знал, как связаться с ним, поскольку он мог быть принятым.

А вот учиться было реально тяжело. Расслабляться можно было не более двух недель, в начале семестра. Потом надо было выбирать или девочки или математика. За неуспеваемость карали жестко, из Университета вылетали даже победители Всесоюзной математической Олимпиады и участники Международной математической Олимпиады. Не говоря уже о ФМШ-истах (выпускниках Физ-мат школы при МГУ). Один парень реально загремел в Кащенко, потом восстановился, но у него «крыша потекла» снова и он оставил мехмат.

На первом курсе нас было 300 человек, на пятом осталось - 150. Из армии, восстановиться на математику уже никто не мог, только на механику. Это дало мне повод сказать, что на математику МГУ поступают только в 17 лет либо никогда. Не считая меня, конечно :) , Я был сильно старше 17 лет, на первом курсе. Но, ничего удержался, хотя первые полгода был на грани вылета. Кстати, на механику поступил 12-летний абитуриент, тоже из Казахстана, но выглядел значительно старше.

В общем, интересное было время, был бы литературный талант – написал бы книгу.
1. adeshere
  10.11.2023 06:46
  #26146500
  Аналогичная история, только на физфаке МГУ. На устном спросили теорему Пифагора, а я забыл школьное доказательство и, немного помучившись, кривенько вывел каким-то наспех придуманным способом. Вполне прокатило. Конкурс был меньше обычного, т.к. из-за олимпиады-80 экзамены во все вузы были совмещены по времени, и это не позволяло, потерпев фиаско в МГУ, пойти сдавать вступительные в другое место. Из-за этого довольно много сильных абитуриентов, не желая рисковать, сразу пошли в ВУЗы попроще. Потом про нас даже присказка появилась:
  
  "олимпийский набор"
  это когда какой-то коллектив оказывается гораздо тупее, чем ожидалось
  А конец одинаковый: несмотря на все усилия преподов, доучилось меньше половины от поступивших...
1. PereslavlFoto
  10.11.2023 06:46
  #26148786
  Вы можете применить вот какой способ. Сначала пишите на Хабре хотя бы небольшие комментарии, просто чтобы наметить интересные точки воспоминаний. Потом пишите здесь статьи, куда соберётся материал на отдельные главы, и главное — лицензируйте их для свободного использования при помощи лицензий Creative Commons. Когда в таких статьях наберётся достаточно много материала, другие люди возьмут ваши тексты, сделают из них книгу и издадут её по указанной вами свободной лицензии.
  1. Emelian
    10.11.2023 06:46
    #26149368
    +2
    Спасибо за интерес к теме!
    
    Я не уверен, что кто-то напишет книгу за меня, даже если я предоставлю максимум материала. Это надо делать самому. Хотя, о своих "интересных точках воспоминаний" я писал много. В Интернете у меня имеется множество подобных текстов, сотни, если не тысячи. Даже здесь, на Хабре, можно найти упоминания, скажем, о том, как я решал квантовое уравнение Шредингера, в общем виде. Началось все еще в первом ВУЗе (Донецкий Политех, о котором я упоминал в других своих комментариях, здесь). Показал свое решение нашему молодому семинаристу по физике - ученику Капицы. Несмотря на его понты в физике, он у меня ошибки искать не захотел. Как не находили ее, при всей примитивности идеи решения, другие выпускники физфака, с которыми я сталкивался. После первого ВУЗа я получил распределение в Белгородский НИИ, где и начал готовится к поступлению в МГУ (в котором должен был отработать не менее трех лет, для этого). Собирался стать физиком-теоретиком, но в последний момент передумал и подал документы на математика (это отдельная история). Так вот, на мою ошибку мне указал, хотя она почти очевидна, мой однокурсник-вундеркинд, на четвертом курсе МГУ. Он сказал о ней раньше, чем я успел сформулировать свое "решение". Вот это я понимаю - уровень!
    
    В книге можно было бы рассказать и моей роковой "московской любви". Я думаю, это было бы круче, чем у Ромео и Джульетты. Моя девушка любила издеваться над молодыми и неопытными студентами. Влюбляла в себя, а когда парень искренне признавался ей в любви - презрительно кидала его. Видимо, в прошлой жизни, мужики сильно достали ее. Кстати, она очень много и с любовью говорила о Грибоедове ("Горе от ума"), такое впечатление, что знала его лично. Не все выдерживали ее издевательств, для некоторых это оборачивалось настоящей трагедией. Когда один осужденный, у которого крыша поехала из-за нее, попросил, в последнем желании, встретиться с ней, она пришла, презрительно глянула не него и ушла, а парень из-за нее и другим жизнь поломал и себе.
    
    Так вот, когда я ее упрекнул, зачем она ломает жизни молодым ребятам, она внимательно посмотрела на меня и спросила: "Хочешь, я сделаю с тобой тоже самое?". Я, с насмешкой (все же был на девять лет старше ее), говорю: "Девушка, у тебя ничего не получится!". Она промолчала, но в глазах прочел: "Получится!". Потом она почти год ухаживала за мной. Все на факультете были в шоке. Парень, говорили мне, за тобой ухаживает такая красавица, а ты носом воротишь! Но я-то знал, чем все это кончится. Через три дня она жестко кинет меня, разбив все мои чувства, если не жизнь. Кстати, то, что я выжил, после общения с ней, я считаю своей главной заслугой.
    
    В конце концов, я не выдержал, чай не железный, и сдался. Согласился на три дня счастья. К моему удивлению, оно продлилось целых три месяца. Главный комплимент, который я услышал от нее: "Ты оказался лучше, чем я думала!". Тем не менее, три месяца прошло, и мы расстались, хотя я даже приезжал к ней в Москву, уже после окончания МГУ. Но она, как всегда была, в своем репертуаре, когда ее любишь, она тебя презирает. Может быть, в моем случае, не так грубо, как других.
    
    Тем не менее, прошло десять лет, пока я более-менее не освободился от ее любви и смог, наконец, жениться.
    
    Еще один интересный случай вспомнил, "раз пошла такая пьянка". Китайское посольство в Москве, пригласило студентов-математиков и меня в том числе, на чаепитие. Мы пришли, нам дали чай и конфеты. Чай был бледный, но очень крепкий и вкусный, а у конфет я не мог снять внутреннюю бумажную обертку. Оказывается, она была растворимой, ее надо было есть вместе с конфетой. Хорошо, у меня спрашивают, как вы относитесь к Хрущеву? Я, по простоте своей душевной, говорю: "Жаль мужика, рано его сняли с должности, не дали ему Коммунизм построить!". Китайцы сразу как-то скисли, ибо Хрущева они сильно не любят. Я, в принципе, это знал, но не считал нужным им подыгрывать. Потом уже, ради вежливости, спрашивают, каких китайских писателей вы знаете? Я отвечаю: "Го Мо Жо". Надо было видеть их лица! Они сразу расцвели и стали на порядок более дружелюбнее. Говорят, у нас в Китае, не все даже слышали о нем. А как я про него узнал? В первом ВУЗе, был парень, фанат литературы (очень интересная личность, про него можно рассказывать много) как то заказал, по каталогу, в Институтской библиотеке, книгу этого автора. Библиотекарша принесла ее со слезами на глазах. Вы, говорит, первый читатель, за 20 лет существования книги, который попросил ее почитать. И рассказала ему историю про Го Мо Жо. В сталинские времена, этот писатель посетил СССР. Какого-то хрена его повезли в детский садик. Детям, строго настрого наказали: "Приедет дядя, скажите хором: "Здравствуй, дядя Го Мо Жо!"". Ладно, дядя приезжает, но не один, а с женой. Ему детишки и говорят: "Здравствуй, дядя Го Мо Жо и Гоможопина тётя!". Такое, конечно, уже не забудешь :) . Но этого, конечно, китайцам я не стал рассказывать.
    
    Были еще интересные истории про немецких студентов у нас и много чего еще. Но все за раз не расскажешь.
    
    Возвращаясь к литературной теме. Естественно, никаких лицензионных ограничений на свои опубликованные тексты и программы я не накладываю. Что касается собственно литературы, то главное, на мой взгляд, это не сюжет и даже не содержание романа, повести или рассказа, а "красивый слог", почти музыкальный. Т.е., нужно уметь писать "красиво" и тогда даже благоглупости пойдут на ура. Есть даже такой литературный стиль - бытовой роман, вроде серии книг: "Весна", "Лето" и др. эстонского писателя Оскара Лутса. Там главное форма, содержание может быть вполне нейтральным. У Лутса все было хорошо, неприятными (которые только и запомнились) были моменты, когда детвора, начитавшись про истребление англосаксами индейцев, снимали скальпы с кошек. Сатанизм, если он есть, его не скроешь.
    
    Короче, чтобы писать книги, нужно учиться писать красиво. А для этого нужно, сначала, научиться говорить красиво. В этом смысле, мне нравятся французы. У них бзик на гуманитарном образовании (у нас на техническом, по крайней мере, в мое время). Поэтому их видео блогеры говорят очень красиво. Например, певица Zaz, с трудом знает арифметику (как и А.С. Пушкин), но интервью дает - заслушаешься!
    
    Кстати, по этой причине, я пытаюсь учить французский язык, но упор делаю на техническое оснащение (компьютерные программы и данные). А, поскольку, путных обучающих программ нет, то пытаюсь писать и публиковать свои. Но пока результат только промежуточный.
    
    Далее, чтобы "писать красиво", можно использовать ИИ, чем, надеюсь, заняться в будущем...

belch84
10.11.2023 06:46
#26147930
Тоже вспомнил свою задачу со вступительного письменного экзамена на мехмат, так скажем, провинциального советского вуза. Нужно было найти значение определенного интеграла от арксинуса на промежутке от 0 до 1. Как все мы хорошо знаем, такой интеграл следует брать по частям, но в те годы интегрирование по частям в школе еще не проходили, поэтому я о нем просто не знал. Тем не менее интеграл этот я вычислил с помощью геометрических соображений - площадь под кривой получается как вычитаемая из площади прямоугольника площадь над кривой, а она соответствует интегралу от синуса

Как искать интеграл от арксинуса

Тот экзамен я сдал не слишком удачно, но все же поступил за счет устной математики, физики и сочинения, конкурс тогда был небольшой.