Из фото в 3D, ч.2: калибровка камеры / forpes.ru

Главная
Из фото в 3D, ч.2: калибровка камеры

Из фото в 3D, ч.2: калибровка камеры +13

16.11.2023 10:04

Ilya12c 0 1800 Источник

В первой части статьи мы немного поупражнялись на яблоках, чтобы понять, как 3D-объекты проецируются на 2D-плоскость фотографии. Заодно мы описали математическую модель камеры и ее параметры.

Знаешь параметры — ~~живешь в Сочи~~ можешь восстановить 3D-сцену или ее характеристики: высоту здания, расстояние до пешехода, загруженность самосвала. Словом, сплошная польза для целого ряда отраслей.

А вот как именно определить эти заветные параметры, так и осталось за кадром. К тому же мы рассматривали простейшую модель pinhole, но в реальной жизни все сложнее. У большинства камер есть линзы, которые искажают изображения (вспомните эффект fisheye). Все эти «рыбьи глаза»‎ и другие отклонения нужно как-то корректировать.

О том, как восстанавливать параметры камеры (калибровать ее) и нивелировать искажения (дисторсию), читайте в этой публикации.

Также из нее вы узнаете:

как выглядит математическая модель калибровки и дисторсии;
как собрать датасет для калибровки;
какие есть методы калибровки;
детали одного из этих методов.

Одна из главных задач машинного зрения — определить ориентацию и положение камеры в пространстве на основе полученного изображения. Результаты ее решения позволяют создать виртуальную сцену с плоским маркером-объектом и точно определить позицию самой камеры. Более того, такой подход помогает устранять искажения на всех ее изображениях. Это особенно актуально в контексте задач виртуальной и дополненной реальности: точно наложить двумерное изображение на плоскость стены или разместить трехмерную модель на поверхности стола.

Рисунок 1. Фото до (слева) и после (справа) калибровки камеры (источник) — *Рисунок 1. Фото до (слева) и после (справа) калибровки камеры (источник*)

На рисунке выше показана фотография, снятая камерой с объективом fish-eye («рыбий глаз»). Он имеет очень широкий угол обзора, что приводит к деформациям изображения. Все выглядит округлым и выпуклым, а перспектива плывет. Слева мы видим фото с такими искажениями, а справа запечатлено то же самое, только уже после процесса калибровки камеры. Калибровка позволяет уменьшить или устранить деформацию и, как следствие, вернуть объекту естественный вид. Как бы это ни походило на рекламу крема от морщин, именно так оно и работает.

Маркеры и датасет

Для калибровки камеры нужно собрать датасет из изображений, созданных по определенным параметрам — только тогда алгоритм даст хороший результат. Поэтому давайте познакомимся с требованиями к датасету. А чтобы лучше их понять, сперва поговорим о маркерах, которые используются в процессе калибровки камеры для определения ее параметров и возможных искажений при формировании картинки.

Маркеры

Все маркеры и их паттерны (множество повторяющихся в определенном порядке маркеров) имеют четкую геометрическую структуру и регулярность. Поэтому они удобны для анализа и коррекции деформаций. Благодаря маркерам мы знаем известные точки в мировых координатах, например, в миллиметрах, и точки в пикселях.

Рассмотреть все существующие маркеры в одной статье не получится, иначе одно перечисление потянет на талмуд. Остановимся на самых основных.

Шахматная доска (chessboard) и ChArUco-маркеры

В случае с шахматной доской необходимо, чтобы вся она попадала в кадр при сборе датасета. Если хотя бы малая ее часть выпадет, алгоритм потеряет один или несколько углов. И тогда шах и мат: не удастся точно соотнести между собой 3D и 2D-точки.

Зато углы шахматной доски (седловые точки) определяются с высокой точностью. Они не подвержены искажениям при перспективных преобразованиях или дисторсии объектива (о ней расскажем ниже).

Важно, что для исключения инвариантности к вращению число строк должно быть четным, а число столбцов — нечетным (или наоборот). Иначе может возникнуть неоднозначность вращения.

Что касается ChArUco, то это смесь шахматной доски и ArUco-маркера, который полностью состоит из ArUco-меток.

ArUco-метками называются уникальные коды, которые обеспечивают устойчивость к ориентации. Также они устойчивы к таким искажениям, как небольшие изменения углов или формы. При использовании ChArUco для отслеживания объектов ArUco-маркеры дают точки, по которым можно достоверно определить положение и ориентацию объектов. А еще благодаря этому паттерну не возникнет проблем при неполном попадании объектов в кадр.

Асимметричный и симметричный паттерны из кружков

Кружки на изображении могут быть обнаружены как blob’ы с помощью OpenCV. При этом есть условия для удаления неправильных кандидатов. Политический PR и предвыборные гонки здесь ни при чем: имеются в виду условия на площадь, окружность и другие.

Асимметричные сетки более предпочтительны для оптимизации геометрии и калибровки стереоизображений. Кружки же, как и эллипсы, подвержены искажениям перспективы и дисторсии. Для точной калибровки необходимо учесть форму эллипсов и центр проекции кругов. Точность в определении кружков в теории выше в сравнении с другими маркерами, так как они могут детектироваться с субпиксельной точностью. Но на практике особой разницы между ними и остальными маркерами мной замечено не было.

*Рисунки 4 и 5: асимметричный и симметричный паттерны*

Для каждого из этих маркеров реально выбрать нужный размер, количество точек и другие параметры. Все зависит от вашей камеры и задачи.

Можно сгенерировать и скачать нужный вам паттерн или сгенерировать свой паттерн при помощи OpenCV. А еще здесь можно почитать про особенности маркеров.

Датасет

С теорией по маркерам хотя бы в общих чертах закончили. Самое время перейти к датасету и практике. Для успешной калибровки камеры нужно следовать ~~внутреннему голосу~~ определенной последовательности действий.

Сперва приготовьте маркер для калибровки. Распечатайте его и аккуратно прикрепите на гладкую поверхность, например, на доску или стену. Никаких искажений на нем быть не должно.

Рисунок 6. Процесс сбора датасета. Доска, сделанная мной во время работы в стартапе PTF Lab в 2019 году. И счастливый и довольный CEO стартапа :)

Затем расположите подготовленную поверхность с маркером в выбранном помещении. Проведите съемку маркера с разных ракурсов и ориентаций. Необходимо представить в вашем датасете разнообразные ракурсы. Тогда камера сможет увидеть маркер под разными углами. Расположите маркер как по центру изображения, так и по его краям. Для каждого положения сделайте несколько снимков, меняя угол обзора и расстояние между камерой и маркером.

Особое внимание следует уделить варьированию расстояний между камерой и маркером, а также размеру маркера на изображении. Это имеет большое значение для учета искажений, которые могут возникнуть при разных условиях

Истинные точки координат маркера (X, Y, 0) мы получаем благодаря знанию о паттерне. Третья координата, отвечающая за глубину, для удобства равна нулю. Ведь нам все равно, где определять мировую систему координат, поэтому точки паттерна можно указать как угодно. Обычно длину ячейки паттерна определяют как единицу следующим образом: (0, 0, 0), (0, 1, 0), (…) (9, 6, 0).

Качество фото и собранного материала очень сильно влияет на уровень калибровки

Если изображения сделаны под слишком острым углом, мы рискуем детектировать намного меньше точек, что безусловно скажется на ошибке. Но следует учитывать, что это зависит от типа маркера. Также ухудшить результат могут световые блики, поэтому желательно использовать для маркеров матовую поверхность.

Сильно влияет на ошибку и количество сделаных изображений. Нужно получить как можно больше картинок для того, чтобы параметры камеры были подобраны лучше.

Но вернемся к нашей последовательности шагов. Далеераспечатайте шаблонна толстой бумаге, которая не будет сильно и легко деформироваться. Можно склеивать несколько распечатанных маркеров, чтобы получить большее количество точек и лучшее качество. Только учтите, чтобы все части маркеров должны быть ортогональны друг другу.

Рисунок 7. Процесс сбора датасета с кружками. Доска, сделанная мной во время работы в стартапе PTF Lab. И уже не такой счастливый CEO стартапа : ) Ошибкой было сделать доску такой маленькой

Результат может испортить автофокус камеры, поэтому его надо отключить. Фокусировка физически перемещает одну или несколько частей стекла внутри вашего объектива, слегка изменяя поле зрения, искажение объектива и оптический центр (principle point).

На моей практике лучшие результаты показывал шахматный маркер. На нем удавалось достичь наименьшей ошибки при фиксированном количестве детектируемых изображений. Наилучший эффект достигался, когда использовалась шахматная доска размером от 10x10 и более — это увеличивает количество точек, которые удается детектировать.

Кому интересно, можно посмотреть пример использования «‎шахматной доски»‎ из доклада Расима Ахунзянова «Калибровка камеры к лидару»:

Рисунки 8 и 9: маркеры — шахматная доска — *Рисунки 8 и 9: маркеры* — шахматная доска

Еще один нюанс: дешевые струйные или лазерные принтеры могут исказить геометрию паттерна маркера. А это крайне нежелательно, ведь функция ошибки — мера смещения в пикселях. То, что не видно глазу, играет важную роль в калибровке. Вот почему лучше использовать профессиональный типографический принтер.

Вдобавок желательно по возможности избегать «сложных» линз. Для зум- или супер широкоугольных объективов требуются гораздо более сложные линзы, чем доступные для использования OpenCV-модели. Поэтому мы рассматриваем модель камеры с точечной диафрагмой (pinhole модель).

Притом в OpenCV алгоритмы по детектированию очень чувствительны к освещению. Если оно чрезмерное, на снимке появляются блики, что усложняет детектирование. В то время как слишком слабое освещение вовсе сводит его на нет.

Кратко подытожим, что важно при сборе датасета:

гладкая поверхность для прикрепления маркера;
различные ракурсы;
варьирование расстояний между камерой и маркером + размер маркера;
не слишком острый угол для изображений;
матовая поверхность маркеров для избегания световых бликов;
количество изображений (делаем побольше);
отключенный автофокус камеры;
типографический принтер;
несложные линзы (по возможности);
не чрезмерное и не слабое освещение.

Следуя этой инструкции, вы сможете эффективно собрать датасет для калибровки камеры и получить точные результаты.

Калибровка одной камеры, или pinhole-модель

И вот после изучения маркеров и сборки датасета мы можем, наконец, переходить к ~~третьей части Марлезонского балета~~ самой калибровке камеры.

Калибровка — это настройка внутренних параметров матрицы камеры K, параметров дисторсии, а также внешних параметров матрицы R и вектора t с использованием набора известных пар точек (Xw, Yw, Zw)T и соответствующих им координат изображения (u, v)T. Она дает “билеты в два конца”: позволяет корректно преобразовывать трехмерные мировые координаты в двумерные на изображении и обратно. Это может быть полезно, например, для разработки и создания систем виртуальной (VR) или аугментированной (AR) реальности.

Существует много способов калибровки камеры. В этой статье мы познакомимся с методом Zhang, названным по имени одного научного сотрудника Microsoft. Такой метод реализован в Matlab и OpenCV. Сейчас мы разберем это аналитическое решение с помощью подхода DLT для одного обзора (single view) и для множественных обзоров (multiple views) камеры. Затем уточним полученные значения и минимизируем функцию потерь.

На всякий случай поясним, что DLT (Direct Linear Transform) — это математический подход на основе линейных алгебраических операций для оценки параметров камеры и преобразования координат. В свою очередь, метод Zhang является модификацией DLT, которая учитывает дисторсию (искажение) объектива и предлагает дополнительные шаги к повышению точности калибрации.

Нотации

Прочитать нотации все же придется, так как без них калибровка не получится. Итак, поехали.

— 2D точка на плоскости;
— 3D точка в мировом пространстве;
— 3D точка в пространстве камеры.

Эти точки будут переводиться в однородные координаты и обозначаться как:

$\tilde{p} = (u, v, 1)^T$
$\tilde P_w = (X_w, Y_w, Z_w, 1)^T$

Отношение между 3D-точкой и точкой на 2D плоскости выглядит так:

$\lambda \tilde p = K[R|t] \tilde P_w$

где:

$\lambda$ — коэффициент масштаба;
и — внешние параметры камеры для перехода из в;
$\tilde{p}$ — точка в однородных координатах;
$\tilde{P_w}$ — точка в однородных координатах;
— внутренние параметры камеры.

Камера представляется таким образом:

$K = \begin{bmatrix} f_u & \gamma & c_u \\ 0 & f_v & c_v \\ 0 & 0 & 1 \\ \end{bmatrix}$

где:

— координата главной точки (principal point);
и — фокусное расстояние и коэффициенты масштаба в осях изображения u и v, которые позволяют учесть масштабные искажения из-за особенностей оптической системы камеры;
$\gamma$ — скос, или параметр, описывающий асимметрию двух осей изображения.

Калибровка камеры аналитическим методом

И снова возвращаемся к нашему подходу DLT для калибровки камеры с одной точки обзора (single view). Идея здесь следующая: приводим уравнение перспективной проекции в однородный и линейный вид и решаем его стандартными методами.

Для каждого изображения существует 3D-2D-отношение пар точек, а также составляется система уравнений следующего вида.

$\lambda\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = K \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ 0 \\ 1 \end{bmatrix} \Rightarrow \lambda\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = K \begin{bmatrix} r_{11} & r_{12} & t_1 \\ r_{21} & r_{22} & t_2 \\ r_{31} & r_{32} & t_3 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ 1 \end{bmatrix}$

Такой метод предполагает присутствие всех точек на одной плоскости (шахматная доска), поэтому в формуле выше Z = 0, а матрица [R|t] меняет размерность с 3x4 на 3х3.

Теперь вводим понятие гомографии. С ним уравнение принимает следующий вид:

$\lambda\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = K \begin{bmatrix} r_{11} & r_{12} & t_1 \\ r_{21} & r_{22} & t_2 \\ r_{31} & r_{32} & t_3 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ 1 \end{bmatrix} \Rightarrow \lambda\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ 1 \end{bmatrix} \Rightarrow \lambda\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = H \begin{bmatrix} X_w \\ Y_w \\ 1 \end{bmatrix}$

где — гомография, которая описывает отношение между двумя проективными преобразованиями.

Затем мы представляем матрицу как 3 вектора где — -ая строка (всего 3 строки и 1 столбец), а как $\tilde{P_w}$ :

$\lambda\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} h_{1}^T \\ h_{2}^T \\ h_{3}^T \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ 1 \end{bmatrix}\Rightarrow \lambda\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} h_{1}^T \\ h_{2}^T \\ h_{3}^T \\ \end{bmatrix} \tilde P_w$

А вот обратное преобразование однородных координат в пиксельные координаты:

$\begin{aligned}& u=\frac{\lambda u}{\lambda}=\frac{h_1^{\mathrm{T}} \cdot \tilde P_w}{h_3^{\mathrm{T}} \cdot \tilde P_w} \\& v=\frac{\lambda v}{\lambda}=\frac{h_2^{\mathrm{T}} \cdot \tilde P_w}{h_3^{\mathrm{T}} \cdot \tilde P_w}\end{aligned} \Rightarrow \quad \begin{aligned}& \left(h_1^{\mathrm{T}}-u_i h_3^{\mathrm{T}}\right) \cdot \tilde P_{wi}=0 \\& \left(h_2^{\mathrm{T}}-v_i h_3^{\mathrm{T}}\right) \cdot \tilde P_{wi}=0\end{aligned}$

Переставив слагаемые, мы получим уравнение для одной точки:

$\begin{aligned}& \left(h_1^{\mathrm{T}}-u_i h_3^{\mathrm{T}}\right) \cdot P_i=0 \\& \left(h_2^{\mathrm{T}}-v_i h_3^{\mathrm{T}}\right) \cdot P_i=0\end{aligned} \quad \Rightarrow \begin{aligned}& P_i^{\mathrm{T}} \cdot h_1+0 \cdot h_2^{\mathrm{T}}-u_i P_i^{\mathrm{T}} \cdot h_3^{\mathrm{T}}=0 \\& 0 \cdot h_1^{\mathrm{T}}+P_i^{\mathrm{T}} \cdot h_2^{\mathrm{T}}-v_i P_i^{\mathrm{T}} \cdot h_3^{\mathrm{T}}=0\end{aligned} \quad \Rightarrow \left[\begin{array}{ccc}P_i^{\mathrm{T}} & 0^{\mathrm{T}} & -u_1 P_i^{\mathrm{T}} \\0^{\mathrm{T}} & P_i^{\mathrm{T}} & -v_1 P_i^{\mathrm{T}}\end{array}\right]\left[\begin{array}{l}h_1 \\h_2 \\h_3\end{array}\right]=\left[\begin{array}{l}0 \\0\end{array}\right]$

Для точек (одно фото или одна точка обзора) мы можем объединить все эти уравнения в большую матрицу:

$\left[\begin{array}{ccc} P_1^{\mathrm{T}} & 0^{\mathrm{T}} & -u_1 P_1^{\mathrm{T}} \\ 0^{\mathrm{T}} & P_1^{\mathrm{T}} & -v_1 P_1^{\mathrm{T}} \\ \cdots & \cdots & \cdots \\ P_n^T & 0^{\mathrm{T}} & -u_n P_n^{\mathrm{T}} \\0^{\mathrm{T}} & P_n^{\mathrm{T}} & -v_n P_n^T \\ \end{array}\right ]\left[\begin{array}{l} h_1 \\h_2 \\h_3 \end{array}\right] = \left[\begin{array}{l} 0 \\ 0 \\ \vdots \\ 0 \\ 0 \end{array}\right] \Rightarrow Q \cdot H = 0$

где — известная матрица, а — неизвестная матрица.

Однозначное решение (Minimal solution):

должен иметь ранг 8 для одного (в пределах масштаба) нетривиального решения;
каждое соответствие точек дает 2 независимых уравнения;
требуется минимум 4 неколлинеарных точки.

Однозначное решение – система, где число уравнений равно числу неизвестных.

Переопределенное решение (Over-determined):

≥ 4 точек;
можно решить с помощью сингулярного разложения SVD.

Переопределенная система — это система, число уравнений которой больше числа неизвестных.

Матрица H может быть декомпозирована для получения K, R, t следующим образом:

$\begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \\ \end{bmatrix} = \begin{bmatrix} f_u & \gamma & c_u \\ 0 & f_v & c_v \\ 0 & 0 & 1 \\ \end{bmatrix}\begin{bmatrix} r_{11} & r_{12} & t_1 \\ r_{21} & r_{22} & t_2 \\ r_{31} & r_{32} & t_3 \\ \end{bmatrix}$

Подчеркнем, что для декомпозиции нужны минимум 2 точки обзора. Как показывает практика, чем больше точек, тем лучше. Для достижения оптимальных результатов калибровки возьмем 20–50 изображений, охватывающих все поле зрения камеры.

Для каждого обзора будет своя гомография , матрица поворота и смещения , . При этом, останется таким же.

$\begin{bmatrix} h_{11}^j & h_{12}^j & h_{13}^j \\ h_{21}^j & h_{22}^j & h_{23}^j \\ h_{31}^j & h_{32}^j & h_{33}^j \\ \end{bmatrix} = \begin{bmatrix} f_u & \gamma & c_u \\ 0 & f_v & c_v \\ 0 & 0 & 1 \\ \end{bmatrix}\begin{bmatrix} r_{11}^j & r_{12}^j & t_1^j \\ r_{21}^j & r_{22}^j & t_2^j \\ r_{31}^j & r_{32}^j & t_3^j \\ \end{bmatrix}$

Теперь нам осталось рассмотреть алгоритм получения параметров камеры из матрицы H для множественных точек обзора:

Оцениваем гомографию для каждого -го представления с помощью алгоритма DLT.
Определяем внутренние параметры по набору гомографий:

каждая гомография дает два линейных уравнения в 6 элементах матрицы
если и ограничения вращения и , то и

Объединяем уравнения из обзоров для получения линейной системы , где — матрица известных нам координат на изображении и мировых координат на шахматной доске.
Решаем уравнение и находим (то есть )
Декомпозируем матрицу и получаем :

$\begin{aligned}c_v & =\left(B_{12} B_{13}-B_{11} B_{23}\right) /\left(B_{11} B_{22}-B_{12}^2\right) \\\lambda & =B_{33}-\left[B_{13}^2+c_v\left(B_{12} B_{13}-B_{11} B_{23}\right)\right] / B_{11} \\ f_u & =\sqrt{\lambda / B_{11}} \\ f_v & =\sqrt{\lambda B_{11} /\left(B_{11} B_{22}-B_{12}^2\right)} \\\gamma & =-B_{12} f_u^2 f_v / \lambda \\c_u & =\gamma c_v / f_v-B_{13} f_u^2 / \lambda\end{aligned}$

Зная внутренние параметры камеры, мы получаем ее внешние параметры:

$\begin{aligned} r_1 & = \lambda K^{-1} h_1 \\ r_2 & = \lambda A^1 h_2 \\ r_3 & = r_1 \times r_2 \\ & t = \lambda K^{-1} h_3\end{aligned}$

где $\lambda$ — коэффициент масштаба.

$\lambda = 1/ ||K^{-1}h_1||= 1/ ||K^{-1}h_2||$

И теперь получаем матрицу вращения

Для однозначного решения (Minimal solution):

матрица ;
каждое соответствие точек дает 2 независимых уравнения;
при будет единственное решение , определенное с точностью до масштабного коэффициента;
при мы сможем вычислить только фокусное расстояние.

Ошибка перепроецирования

Чтобы оценить, как же работает наш алгоритм, нужно вычислить ошибку перепроецирования (reprojection error). Это евклидово расстояние в пикселях между наблюдаемой точкой изображения и соответствующей трехмерной точкой, перепроецированной на кадр камеры. Ошибка перепроецирования дает нам количественную меру точности калибровки, которая в идеале равна нулю.

Параметры калибровки , определенные с помощью DLT, можно уточнить путем минимизации функции потерь (по сути, именно здесь на сцену выходит метод Zhang):

$\text{reprojection error} = \sum_{i=1}^n\sum_{j=1}^m \|p_{ij} - p_{\text{proj}}(K, R_i, t_i, P_{w}^j)\|^2$

где даны изображений плоскости модели. На плоскости модели имеется точек, а $p_{\text{proj}}(K, R_i, t_i, P_{w}^j)$ — проекция точки $P_{w}^j$ на изображении согласно уравнению:

$\lambda \tilde p = K[R|t] \tilde P_w$

*Рисунок 12. Уточнение внутренних и внешних параметров камеры*

И тут мы подошли к еще одному внутреннему параметру камеры — дисторсии.

Дисторсия

Дисторсия (distortion) — это искажение изображения, вызванное несоответствием между фактической геометрией объектов в сцене и их представлением на фотографии. Придирчивые любители сделать красивые селфи поймут =). Дисторсия проявляется из-за физических характеристик камеры и объектива, которые могут привести к деформациям в углах, длинах и формах объектов на изображении.

Основная причина дисторсии — использование оптических систем, где линзы и зеркала могут вносить аномалии в прохождение света.

Есть несколько видов дисторсии, каждый из которых имеет отличительные характеристики и в разной степени влияет на картинку. Давайте рассмотрим некоторые из них:

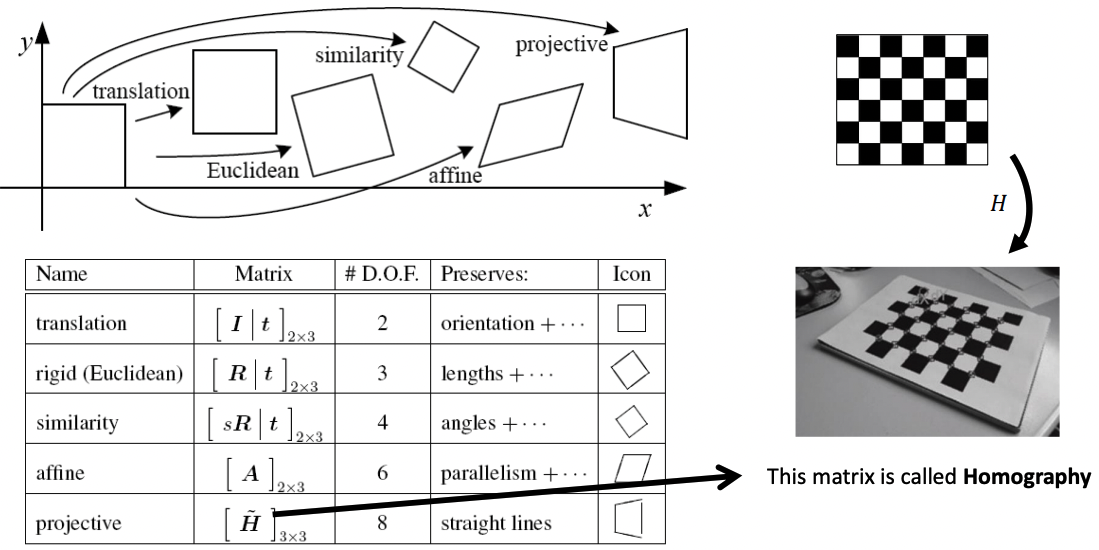
Радиальная дисторсия, или искривление объектива (Radial distortion): объекты на краях кадра могут быть изогнуты или растянуты. Она может быть бочкообразной (объекты сжимаются к центру кадра) или подушкообразной (объекты вытягиваются от центра кадра).

Рисунки 13 и 14: бочкообразная (Barrel) и подушкообразная (Pincushion) дисторсия

$\begin{align*}x_{\text{distorted}} &= x \left(1 + k_1 \cdot r^2 + k_2 \cdot r^4\right) \\y_{\text{distorted}} &= y \left(1 + k_1 \cdot r^2 + k_2 \cdot r^4\right)\end{align*}$

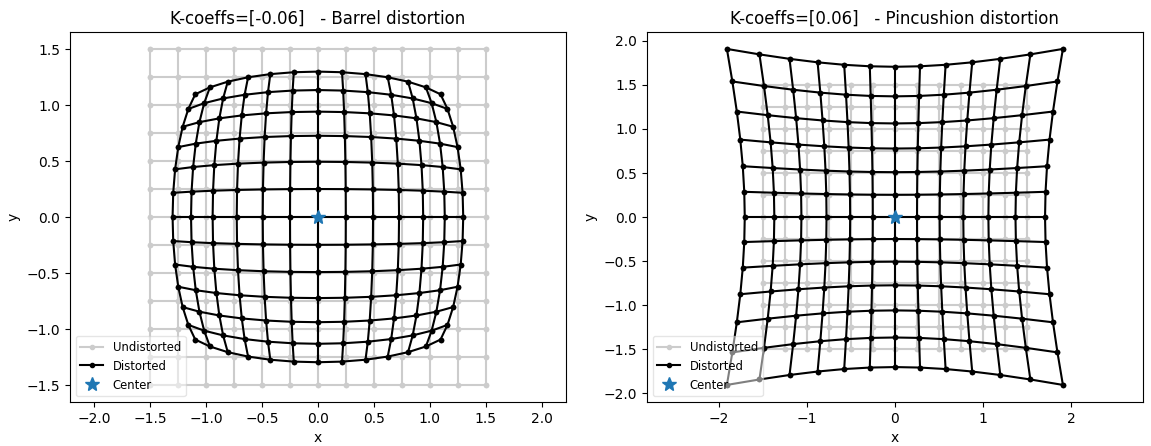
где — расстояние от пикселя изображения до главной точки (principal point), — дополнительные нелинейные параметры радиальной дисторсии.

Тангенциальная, или перспективная дисторсия (Tangential distortion): неправильное положение объектива относительно плоскости изображения. Она может привести к наклону вертикальных или горизонтальных линий, которые начинают казаться искривленными.

Рисунки 15 и 16: тангенциальная дисторсия

$\begin{align*}x_{\text{distorted}} &= x + [2 \cdot p_1 \cdot x \cdot y + p_2 \cdot (r^2 + 2 \cdot x^2)] \\y_{\text{distorted}} &= y + [p_1 \cdot (r^2 + 2 \cdot y^2) + 2 \cdot p_2 \cdot x \cdot y]\end{align*}$

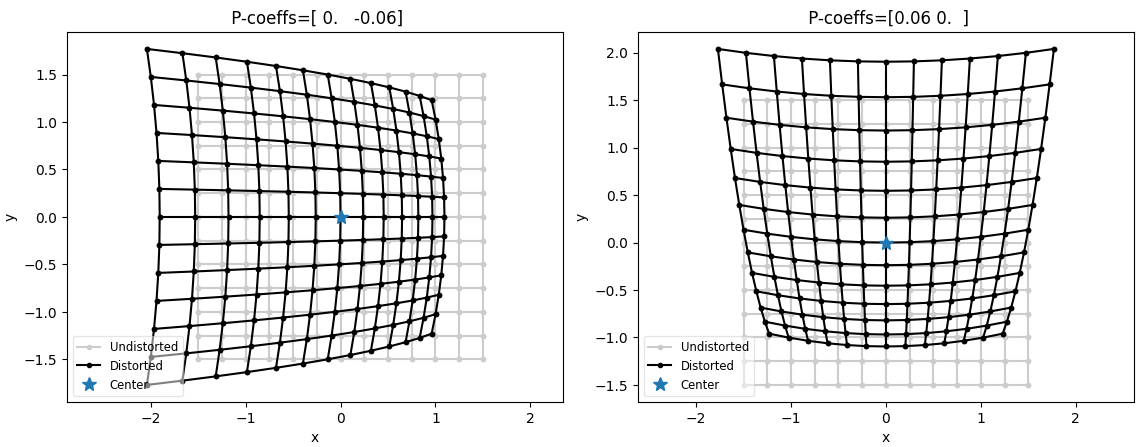
где — расстояние от пикселя изображения до главной точки (principal point), — дополнительные нелинейные параметры тангенциальной дисторсии.

Возвращаемся к pinhole

Модель линейной камеры (pinhole) — идеальная модель проекции, которая не учитывает искажения объектива при проецировании 3D точки на плоскость изображения. Для моделирования искажения проецируемой точки 2D пикселя с помощью pinhole нам нужно сначала оценить нормализованные координаты 2D точек $(\bar{u}, \bar{v})^T$ . Для этого мы можем использовать калибровочную матрицу со следующим выражением:

$\begin{bmatrix} \bar{u} \\ \bar{v} \\ 1 \end{bmatrix}= K^{-1} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix}$

Нормализованная искаженная точка $(\bar{u}_{distorted}, \bar{v}_{distorted})$ определяется как:

$\begin{align*} \begin{bmatrix} \bar{u}_d \\ \bar{v}_d \end{bmatrix} &= \frac{ 1 + k_1 \cdot r^2 + k_2 \cdot r^4 + k_3 \cdot r^6 }{ 1 + k_4 \cdot r^2 + k_5 \cdot r^4 + k_6 \cdot r^6 } \begin{bmatrix} \bar{u} \\ \bar{v} \end{bmatrix} \\ &\quad+ \left[ \frac{2 \cdot p_1 \cdot \bar{u} \cdot \bar{v} + p_2 \cdot (r^2 + 2 \cdot \bar{u}^2)}{2 \cdot p_2 \cdot \bar{u} \cdot \bar{v} + p_1 \cdot (r^2 + 2 \cdot \bar{v}^2)} \right] \end{align*}$

где — 2D точка пикселя, $(\bar{u}, \bar{v})^T$ — нормализованные координаты 2D точки камеры,— коэффициенты радиальной дисторсии (параметров больше для учета более сильной дисторсии), — коэффициенты тангенциальной дисторсии, $r = \bar{u}^2 + \bar{v}^2$ — расстояние от пикселя изображения до главной точки (principal point).

Далее нам просто нужно вернуться к исходному (ненормализованному) пиксельному пространству. Для этого мы можем использовать внутреннюю матрицу :

$\begin{bmatrix} u_d \\ v_d \\ 1 \end{bmatrix}= K \begin{bmatrix} \bar{u}_d \\ \bar{v}_d \\ 1 \end{bmatrix}$

Таким способом мы смоделировали радиальное и тангенциальное искажения для линейной модели камеры (pinhole).

Чтобы компенсировать деформацию объективом набора двумерных точек (оценить неискаженные координаты для заданного набора искаженных точек), нам нужно инвертировать нашу модель искажения.

Как учитывать радиальную дисторсию?

Нам нужно учитывать m точек на n изображениях и складывать все уравнения, чтобы получить уравнений, или , где в матричной форме.

Линейное решение методом наименьших квадратов выглядит так:

$k = (D^TD)^{-1}D^Td$

Теперь у нас функция потерь представляется следующим образом:

$\text{reprojection error} = \sum_{i=1}^n\sum_{j=1}^m \|p_{ij} - p_{\text{proj}}(K,k_1,k_2,R_i, t_i, P_{w}^j)\|^2$

Заключение

Итого, мы с вами познакомились с дисторсией, калибровкой камеры, практическими советами по сбору датасета и калибровке, DLT-методом калибровки и ошибкой перепроецирования.

Поскольку повторение — мать учения, давайте закрепим порядок действий при калибровке камеры:

Распечатать калибровочный паттерн и наклеить его на твердую плоскость;
Сделать много разных фото (20-50 изображений), двигая камеру или паттерн в пространстве (математически здесь никакой разницы нет);
Получить координаты точек на паттерне;
Получить внутренние и внешние параметры камеры с помощью DLT-метода;
Получить коэффициенты радиального и других искажений путем решения линейного МНК;
Уточнить все параметры, минимизировав функцию потерь.

Теперь вы можете пользоваться этим алгоритмом для успешной калибровки камеры ????

Полезные ссылки

Если вы хотите попробовать откалибровать камеру, то в качестве основного инструмента можно использовать OpenCV, в котором есть все необходимые опции. Он предоставляет объекты для каждого из маркеров, и в каждом объекте есть своя функция калибровки.
Кроме того, можно использовать библиотеку Kornia. Там тоже реализованы методы калибровки для разных видов камеры, а заодно подход DLT.
Создать дисторсии на примере тех, что представлены выше, можно при помощи этой библиотеки.
Cсылка на раздел калибровки с библиотекой Kornia.
Доклад Расима Ахунзянова «Калибровка камеры к лидару».
Список статей и реализаций под разные фреймворки.
Генерация своего паттерна с OpenCV и генерация паттерна через UI.
И еще можно больше почитать про DLT за 5 минут и про особенности маркеров.

Что изучить дальше

Исследование 2000 года про метод Zhang.
12 бесплатных лекций по фотограмметрии (трехмерная реконструкция).
Много лекций по фотограмметрии в компьютерном зрении и не только.

Первая версия статьи написана для deepschool-pro, на Хабре публикуется с изменениями и дополнениями.