(мифы и нереальности)

Задание: необходимо прочитать Micro QR Code версии М3, содержащий кодовое слово, на примере закодированных слов – АБВГДЕ, абвгде, АБВГ и абвг (почему именно такое количество символов будет расшифровано далее), на основе алгоритмов, приведенных в ГОСТ Р ИСО/МЭК 18004-2015 (п. 7.4, алфавитно-цифровой и/или байтовый режим). Аналогично версий М1 и М2 данный режим невозможно прочитать стандартными ресурсами мобильных устройств, производимых GAFAM (Ассоциация отказалась и от этого режима).

Примечание: здесь и далее будет использоваться информация ГОСТ Р ИСО/МЭК 18004-2015, в оригинале ISO/IEC 18004:2015 кодовой таблицы кириллицы не существует (далее – ГОСТ).

 Этап 0. Подготовка исходных данных

Рассмотрим М3 поближе. Имеем матрицу размерностью 15x15 бинарных символов (рис. 11 ГОСТ), один индикатор и два определителя (горизонтальный и вертикальный) (рис. 1).

Первый наносимый ограничитель символ на матрицу М3 – битовые последовательности информации о формате (рис. 2). Чтение битовой последовательности начинается с 14 бита, т.е. последовательность чтения/записи будет 14, 13, 12, 11, 10 и т.д.

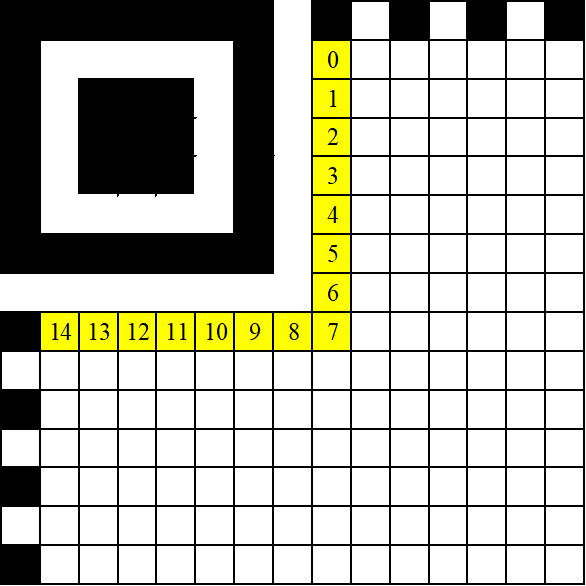
Второй не менее важный элемент М3 – маршрут последовательности заполнения битами данных поля матрицы (рис. 3). Данная схема отражена на рисунке 11 ГОСТ.

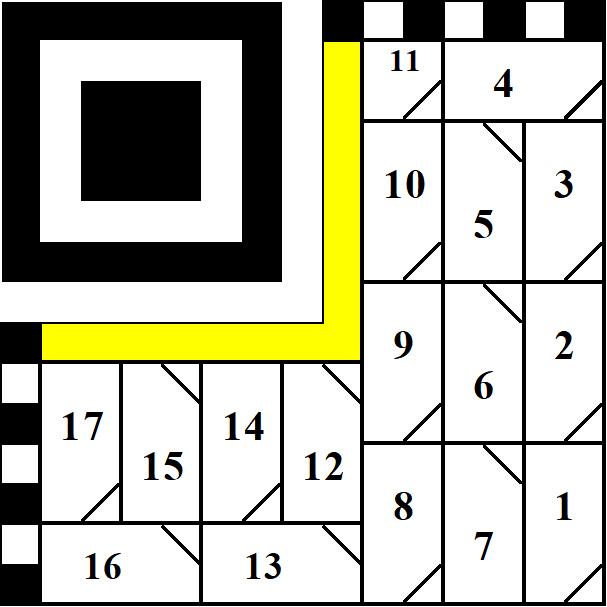
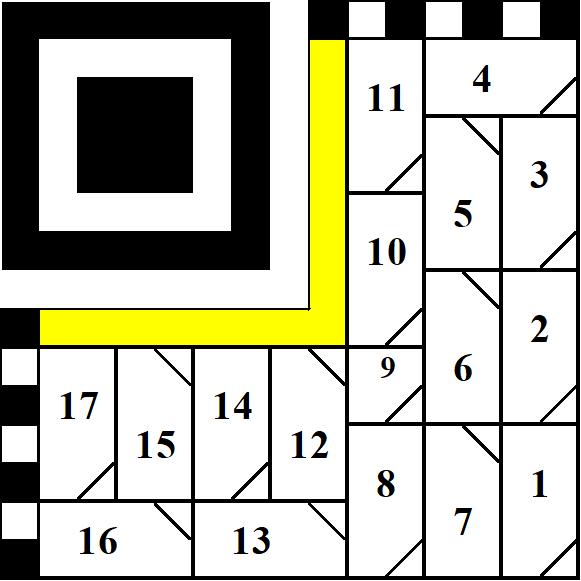
Примечание: приведенные в ГОСТ маршруты для M3-M и M3-L практически одинаковые. Если присмотреться внимательнее, то оба маршрута дублируют друг друга и не вносят изменения в последовательность чтения/записи. Единственное различие – это учет блока в 4-бита для RS-алгоритма (9 и 11 блоки). Далее приводится вариант маршрутов для M3-M и M3-L, примененные в распространяемом бесплатном модуле Ассоциации (рис. 4). Маршруты идентичны и не совпадают с приведенными в ГОСТ (ноу-хау программистов моделистов).

Если наложить маршрут на матрицу, получаем последовательность из 124 бит кода М3 (рис. 4). Число 124 пригодится позже при добавлении кода по алгоритму Рида-Соломона на поле Галуа.

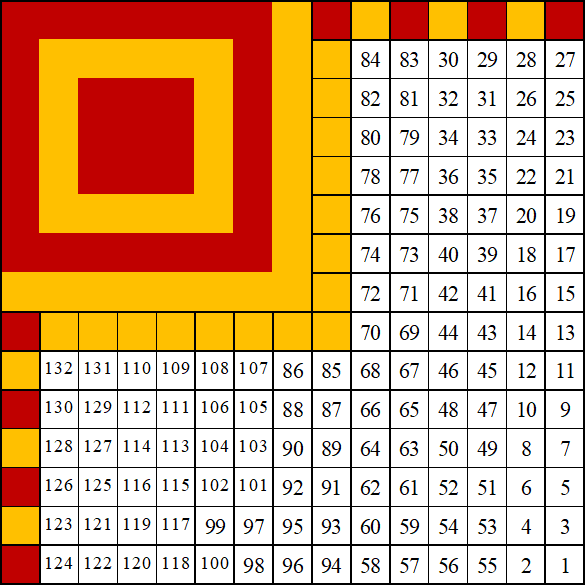
Примечание: здесь и далее будем использовать один из доступных программных инструментов Ассоциации практически на любом ПК – MS Excel (русскоязычная версия). Как следствие, все команды автоматизации процессов будут на кириллице.

Примечание: для удобства дальнейшего описания ссылок на ячейки листа перейдем от современного отображения адресов ячеек в виде R1C1 (относительные ссылки) к старому формату в виде A1 (буквенно-числовое отображение). Выбираем в Меню Файл → Параметры. В категории Формулы в группе Работа с формулами снимаем галочку напротив пункта Стиль ссылок R1C1. В результате названия столбиков должны поменяться с чисел на латинские буквы (рис. 5).

Запускаем программное приложение MS Excel. Готовим последовательность листов Книги для дальнейшей работы:

-     Лист1 – называем Code;

-     Лист2 – M3 АБВГДЕ;

-     Лист3 – M3 абвгде;

-     Лист4 – M3 АБВГ;

-     Лист5 – М3 абвг.

Лист1 (Code) – для размещения корректирующих данных и сверки полученных на листах результатов. Листы 2, 3, 4 и 5 нужны для декодирования соответствующих последовательностей.

На полях листов Лист2 – Лист5 делаем размерность ячеек одинаковой (например, 23 на 23 пикселя) и по горизонтали, и по вертикали (рис. 5a). Затем закрашиваем поле серым фоновым цветом (рис. 5b).

Если посчитать количество пикселей (квадратиков) микрокода М3 (рис. 1) по горизонтали и/или по вертикали, то получится матрица (табличка) размерностью 15×15. Создадим новую схему шаблон для микрокода М3 на Лист2 – Лист4 начиная с ячейки D4 (рис. 6).

На просторах всемирной сети обнаружено всего две разновидности свободно распространяемых библиотек для генерации Micro QR Code. Примеры веб-ресурсов:

-      Генератор Micro QR кодов или QR Code and 2D Code Generator ‑ первый тип библиотек сети Интернет (примеры);

-      Micro QR Код ‑ второй тип библиотек сети Интернет (пример).

Воспользуемся кодировщиками микрокодов в Интернет или рисунками далее для переноса битовой маски рабочего поля микрокода на листы книги MS Excel (рис. 7-8). Почему такие существенные различия между схемами на рисунках будет рассмотрено несколькими этапами далее.

Согласно ГОСТ получается так, что можно использовать только байтовую систему кодирования для выполнения требований задания. В алфавитно-цифровом алфавите не существует символов кириллицы. В задании добавлено следующее ограничение – необходимо кодировать 6 символов и 4 символа алфавита. Воспользуемся таблицей кодировки (Таблица ДА.3 ГОСТ или ISO 8859-5) и алгоритмом, представленном в ГОСТ (п. 7.4.5). Представим символы в виде битовых последовательностей. Получаем следующие комбинации:

-     АБВГ – 10110000 10110001 10110010 10110011;

-     АБВГДЕ – 10110000 10110001 10110010 10110011 10110100 10110101;

-     абвг – 11010000 11010001 11010010 11010011;

-     абвгде – 11010000 11010001 11010010 11010011 11010100 11010101.

Необходимо учесть, что М3 поддерживает два уровня исправления ошибок – L и M. Обращаемся к таблице 7 ГОСТ, получаем, что уровни L и M поддерживают емкость из 4 и 6 символов. Более рациональным будет уровень М, но не будем так спешить (табл. 1).

Таблица 1 – Число знаков символа и емкость входных данных для QR Code (Таблица 7 ГОСТ)

Исходные данные для декодирования готовы. Переходим к заполнению первого листа книги Code.

Открываем лист Code. Пример готового результата представлен на рисунке 9.

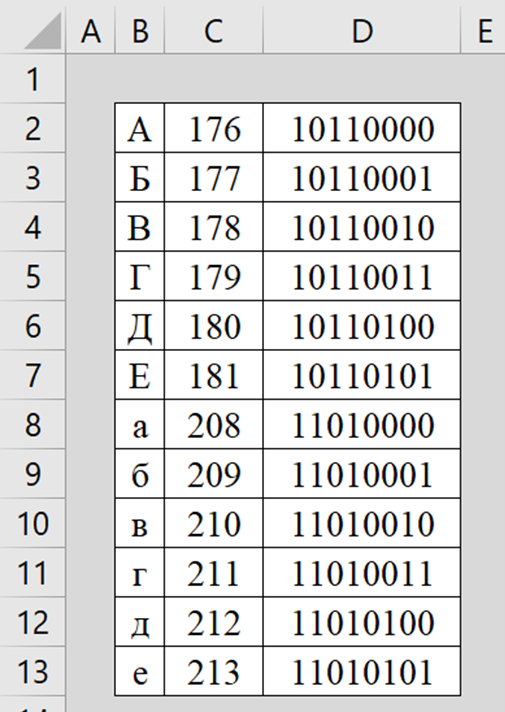
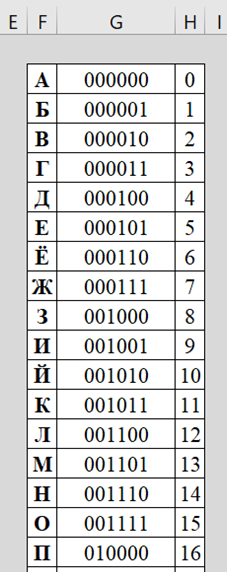
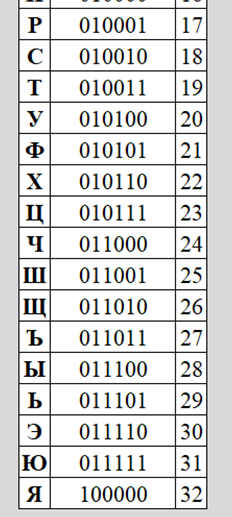
Для автоматизации сначала переносим таблицу символов (табл. 2), начиная с ячейки B2. В диапазоне ячеек B2:B13 алфавит кириллических букв А…Е, затем а…е. В диапазоне ячеек C2:C13 соответствующие десятичный значения по таблице Таблица ДА.3 ГОСТ.

Таблица 2 – Кодирование/декодирование для байтового режима (Таблица ДА.3 ГОСТ, выборка)

Заполняем диапазон ячеек D2:D13. В ячейку D2 добавляем функцию перевода из десятичного числа в двоичное из восьми разрядов:

=ОСНОВАНИЕ(C2;2)

Размножаем за нижний правый угол ячейки D2 (магический квадрат) функцию до ячейки D13. Полученный результат должен соответствовать значениям диапазона на рисунке 9.

Лист с корректирующими данными готов. Переходим к основным микрокодам. Открываем лист книги М3 АБВГДЕ с исходным битовым полем (рис. 10a). К сожалению, за долгие годы MS Excel так и не научился работать с цветом ячеек. Добавим в каждую цветную ячейку соответствующее битовое значение: белая ячейка – 0, черная ячейка – 1 (рис. 10b).

Для удобства отделим цветом индикатор служебной информации (рис. 11a) – битовая последовательность информации о формате. Чтение последовательности начинается с 14 бита, т.е. последовательность чтения будет 14, 13, 12, 11, 10 и т.д.

Также отделяем цветом индикатор распознавания микрокода (рис. 11b).

Полученная матрица готова для дальнейшего анализа (рис. 12).

Переходим к первому этапу – работа со служебной информацией.

 Этап 1. Служебная информация

Перед тем как начать работать с основной рабочей областью микрокода, необходимо расшифровать служебную информацию. Пример итогового результата приведен на рисунке 13.

Сначала переводим служебную информацию также в бинарное представление, т.е. ряды ячеек E12-L12 и L5-L12 представляем как набор 0 (светлые ячейки) и 1 (темные ячейки) (рис. 13).

Выносим служебную информацию из микрокода, т.е. дублируем полученный ряд в угловом представлении и в представлении – один ряд. Получаем следующие ссылочные ячейки:

Воспользуемся рядом бит служебной информации 14 строки для определения версии и уровня микрокода, а также для получения вида используемой в данном коде маски. Сначала найдем соответствие в таблице ГОСТ, потом сделаем самопроверку.

Объединяем ячейки T16-AH16. В полученную новую ячейку T16 добавляем функцию (рис. 13):

=СЦЕП(T14:AH14)

По таблице С.1 ГОСТ (табл. 3) находим битовую последовательность информации о формате и соответствующую последовательность бит данных до маскирования. Для данного примера – 01110.

Hidden text

Таблица 3 – Корректирующие последовательности информации о формате

Последовательность до маскирования		Последовательность после маскирования (символы Micro QR Code)
Биты данных	Биты исправления ошибок	Двоичная	Шестнадцатеричная
00000	0000000000	100010001000101	4445
00001	0100110111	100000101110010	4172
00010	1001101110	100111000101011	4Е2В
00011	1101011001	100101100011100	4В1С
00100	0111101011	101010110101110	55АЕ
00101	0011011100	101000010011001	5099
00110	1110000101	101111111000000	5FC0
00111	1010110010	101101011110111	5AF7
01000	1111010110	110011110010011	6793
01001	1011100001	110001010100100	62А4
01010	0110111000	110110111111101	6DFD
01011	0010001111	110100011001010	68СА
01100	1000111101	111011001111000	7678
01101	1100001010	111001101001111	734F
01110	0001010011	111110000010110	7С16
01111	0101100100	111100100100001	7921
10000	1010011011	000011011011110	06DE
10001	1110101100	000001111101001	03Е9
10010	0011110101	000110010110000	0CB0
10011	0111000010	000100110000111	0987
10100	1101110000	001011100110101	1735
10101	1001000111	001001000000010	1202
10110	0100011110	001110101011011	1D5B
10111	0000101001	001100001101100	186С
11000	0101001101	010010100001000	2508
11001	0001111010	010000000111111	203F
11010	1100100011	010111101100110	2F66
11011	1000010100	010101001010001	2А51
11100	0010100110	011010011100011	34E3
11101	0110010001	011000111010100	31D4
11110	1011001000	011111010001101	3E8D
11111	1111111111	011101110111010	ЗВВА

Проверим полученный результат. Заполняем ячейки в соответствии с таблицей:

Воспользуемся алгебраической функцией XOR для получения версии и уровня микрокода, и кода маски. Заполняем ячейки восьмой строчки:

В результате получаем последовательность 01110, полностью соответствующую полученной по таблице ГОСТ. Расшифруем полученную комбинацию. Разделим на две части: 011 и 10 (3 и 2 бита соответственно). Обратимся к таблице 13 ГОСТ (табл. 4).

Таблица 4 – Номер символа для Micro QR Code

Получаем, что в данном микрокоде используется версия М3 и уровень L, т.е. комбинация M3-L. Запомним, на последующих этапах данная информация пригодится. Уже странно, М уровень был бы намного рациональнее, но данный проблемный «секрет» будет раскрыт чуть позже.

Разбираем вторую часть служебной информации, комбинацию маски 10. Обратимся к рисунку 22 ГОСТ. Перенесем маску с соответствующим битовым кодом на Лист, начиная с ячейки AL4 (рис. 14).

Аналогично основной матрице, каждая черная ячейка обозначена как 1, а каждая белая – 0.

Все необходимые данные на основе служебной информации получены, переходим ко 2-му этапу.

 Этап 2. Расшифровка данных основной рабочей области

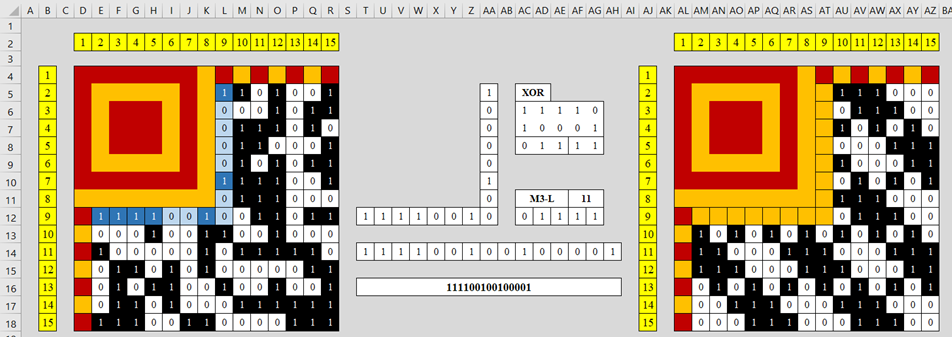
 На основе матрицы исходных данных в диапазоне ячеек D4:R18 и матрицы маскирования в диапазоне ячеек AL4:AZ18 получаем матрицу немаскированных данных в диапазоне ячеек D22:R36 с использованием функции XOR. Пример готового результата представлен на рисунке 15.

В ячейке M23 добавлена следующая формула:

=БИТ.ИСКЛИЛИ(M5;AU5)

Далее за нижний правый угол выделенной ячейки (магический квадрат) дублируем данную формулу на всю поверхность рабочей матрицы. В результате получаем немаскированный вариант для диапазона ячеек M23:R36 и E31:K36.

Самый простой вариант для подготовки к следующему этапу, перенести полученную немаскированную матрицу в таблицу символов вручную. Но это не так интересно. Подготовим таблицу маршрута и заготовку для заполнения битовых комбинаций с учетом особенностей байтового режима.

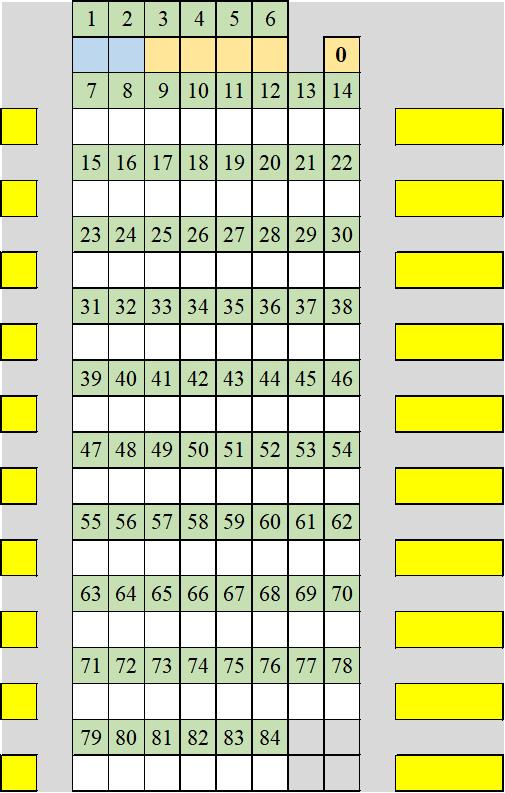
Перенесем маршрут (рис. 4) на Лист MS Excel, начиная с ячейки AL22, где каждую ячейку подпишем соответствующим числовым значением. Результат представлен на рисунке 16.

Напомню: не обязательно каждую ячейку прописывать вручную. MS Excel умеет строить прогрессии. Например, заполняем ячейки AZ36 и AZ35 значениями 1 и 3 соответственно. Затем выделяем заполненные ячейки AZ36:AZ35 и за магический квадратик выделенного диапазона (нижний правый угол ячейки) тянем до ячейки AZ23. В результате весь ряд будет заполнен. Остальное рабочее поле можно заполнить аналогичным образом.

Начиная с ячейки U22 в диапазоне ячеек U22:AH35 делаем шаблон-заготовку для последующего наполнения битовой комбинацией в байтовом режиме. Пример полученного результата представлен на рисунке 17 (цветовая дифференциация произвольная). Цветом отделена служебная информация и кодовая комбинация декодируемого числа.

Так как этой информации достаточно для расшифровки сообщения, переходим к третьему этапу.

 Этап 3. Преобразование кода в набор символов

 Пример варианта по ГОСТ представлен на рисунке 18. Как можно увидеть результат, полное несовпадение с кодовыми значениями Таблицы ДА.3 ГОСТ. Следовательно (забегая вперед), можно уже сделать вывод, что программисты моделисты проявили творческий потенциал и использовали скрытые (не по ГОСТ) алгоритмы.

Тем не менее, сначала пройдем полный маршрут по ГОСТ, а потом на основе полученной последовательности декодирования найдем тот самый скрытый «секретный» искусственный алфавит Ассоциации.

Как было упомянуто ранее, битовые комбинации в диапазон ячеек U22:AH35 можно перенести вручную (простой вариант). Но можно и автоматизировать. Таблица функций заполнит битовые ячейки автоматически (табл. 5).

Hidden text

Таблица 5 – Функциональные ячейки битовых последовательностей

№ п/п	Ячейка	Функция
Первая строка
1.	W23	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(W22;$AZ$23:$AZ$36;0);ПОИСКПОЗ(W22;AM36:AZ36;0))
2.	X23	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(X22;$AY$23:$AY$36;0);ПОИСКПОЗ(X22;AM36:AZ36;0))
3.	Y23	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Y22;$AZ$23:$AZ$36;0);ПОИСКПОЗ(Y22;AM35:AZ35;0))
4.	Z23	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Z22;$AY$23:$AY$36;0);ПОИСКПОЗ(Z22;AM35:AZ35;0))
5.	AA23	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AA22;$AZ$23:$AZ$36;0);ПОИСКПОЗ(AA22;AM34:AZ34;0))
6.	AB23	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AB22;$AY$23:$AY$36;0);ПОИСКПОЗ(AB22;AM34:AZ34;0))
Вторая строка
7.	W25	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(W24;$AZ$23:$AZ$36;0);ПОИСКПОЗ(W24;AM33:AZ33;0))
8.	X25	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(X24;$AY$23:$AY$36;0);ПОИСКПОЗ(X24;AM33:AZ33;0))
9.	Y25	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Y24;$AZ$23:$AZ$36;0);ПОИСКПОЗ(Y24;AM32:AZ32;0))
10.	Z25	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Z24;$AY$23:$AY$36;0);ПОИСКПОЗ(Z24;AM32:AZ32;0))
11.	AA25	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AA24;$AZ$23:$AZ$36;0);ПОИСКПОЗ(AA24;AM31:AZ31;0))
12.	AB25	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AB24;$AY$23:$AY$36;0);ПОИСКПОЗ(AB24;AM31:AZ31;0))
13.	AC25	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AC24;$AZ$23:$AZ$36;0);ПОИСКПОЗ(AC24;AM30:AZ30;0))
14.	AD25	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AD24;$AY$23:$AY$36;0);ПОИСКПОЗ(AD24;AM30:AZ30;0))
Третья строка
15.	W27	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(W26;$AZ$23:$AZ$36;0);ПОИСКПОЗ(W26;AM29:AZ29;0))
16.	X27	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(X26;$AY$23:$AY$36;0);ПОИСКПОЗ(X26;AM29:AZ29;0))
17.	Y27	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Y26;$AZ$23:$AZ$36;0);ПОИСКПОЗ(Y26;AM28:AZ28;0))
18.	Z27	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Z26;$AY$23:$AY$36;0);ПОИСКПОЗ(Z26;AM28:AZ28;0))
19.	AA27	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AA26;$AZ$23:$AZ$36;0);ПОИСКПОЗ(AA26;AM27:AZ27;0))
20.	AB27	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AB26;$AY$23:$AY$36;0);ПОИСКПОЗ(AB26;AM27:AZ27;0))
21.	AC27	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AC26;$AZ$23:$AZ$36;0);ПОИСКПОЗ(AC26;AM26:AZ26;0))
22.	AD27	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AD26;$AY$23:$AY$36;0);ПОИСКПОЗ(AD26;AM26:AZ26;0))
Четвертая строка
23.	W29	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(W28;$AZ$23:$AZ$36;0);ПОИСКПОЗ(W28;AM25:AZ25;0))
24.	X29	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(X28;$AY$23:$AY$36;0);ПОИСКПОЗ(X28;AM25:AZ25;0))
25.	Y29	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Y28;$AZ$23:$AZ$36;0);ПОИСКПОЗ(Y28;AM24:AZ24;0))
26.	Z29	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Z28;$AY$23:$AY$36;0);ПОИСКПОЗ(Z28;AM24:AZ24;0))
27.	AA29	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AA28;$AZ$23:$AZ$36;0);ПОИСКПОЗ(AA28;AM23:AZ23;0))
28.	AB29	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AB28;$AY$23:$AY$36;0);ПОИСКПОЗ(AB28;AM23:AZ23;0))
29.	AC29	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AC28;$AX$23:$AX$36;0);ПОИСКПОЗ(AC28;AM23:AZ23;0))
30.	AD29	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AD28;$AW$23:$AW$36;0);ПОИСКПОЗ(AD28;AM23:AZ23;0))
Пятая строка
31.	W31	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(W30;$AX$23:$AX$36;0);ПОИСКПОЗ(W30;AM24:AZ24;0))
32.	X31	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(X30;$AW$23:$AW$36;0);ПОИСКПОЗ(X30;AM24:AZ24;0))
33.	Y31	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Y30;$AX$23:$AX$36;0);ПОИСКПОЗ(Y30;AM25:AZ25;0))
34.	Z31	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Z30;$AW$23:$AW$36;0);ПОИСКПОЗ(Z30;AM25:AZ25;0))
35.	AA31	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AA30;$AX$23:$AX$36;0);ПОИСКПОЗ(AA30;AM26:AZ26;0))
36.	AB31	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AB30;$AW$23:$AW$36;0);ПОИСКПОЗ(AB30;AM26:AZ26;0))
37.	AC31	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AC30;$AX$23:$AX$36;0);ПОИСКПОЗ(AC30;AM27:AZ27;0))
38.	AD31	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AD30;$AW$23:$AW$36;0);ПОИСКПОЗ(AD30;AM27:AZ27;0))
Шестая строка
39.	W33	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(W32;$AX$23:$AX$36;0);ПОИСКПОЗ(W32;AM28:AZ28;0))
40.	X33	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(X32;$AW$23:$AW$36;0);ПОИСКПОЗ(X32;AM28:AZ28;0))
41.	Y33	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Y32;$AX$23:$AX$36;0);ПОИСКПОЗ(Y32;AM29:AZ29;0))
42.	Z33	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Z32;$AW$23:$AW$36;0);ПОИСКПОЗ(Z32;AM29:AZ29;0))
43.	AA33	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AA32;$AX$23:$AX$36;0);ПОИСКПОЗ(AA32;AM30:AZ30;0))
44.	AB33	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AB32;$AW$23:$AW$36;0);ПОИСКПОЗ(AB32;AM30:AZ30;0))
45.	AC33	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AC32;$AX$23:$AX$36;0);ПОИСКПОЗ(AC32;AM31:AZ31;0))
46.	AD33	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AD32;$AW$23:$AW$36;0);ПОИСКПОЗ(AD32;AM31:AZ31;0))

№ п/п	Ячейка	Функция
Седьмая строка
47.	W35	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(W34;$AX$23:$AX$36;0);ПОИСКПОЗ(W34;AM32:AZ32;0))
48.	X35	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(X34;$AW$23:$AW$36;0);ПОИСКПОЗ(X34;AM32:AZ32;0))
49.	Y35	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Y34;$AX$23:$AX$36;0);ПОИСКПОЗ(Y34;AM33:AZ33;0))
50.	Z35	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Z34;$AW$23:$AW$36;0);ПОИСКПОЗ(Z34;AM33:AZ33;0))
51.	AA35	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AA34;$AX$23:$AX$36;0);ПОИСКПОЗ(AA34;AM34:AZ34;0))
52.	AB35	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AB34;$AW$23:$AW$36;0);ПОИСКПОЗ(AB34;AM34:AZ34;0))
53.	AC35	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AC34;$AX$23:$AX$36;0);ПОИСКПОЗ(AC34;AM35:AZ35;0))
54.	AD35	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AD34;$AW$23:$AW$36;0);ПОИСКПОЗ(AD34;AM35:AZ35;0))
Восьмая строка
55.	W37	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(W36;$AX$23:$AX$36;0);ПОИСКПОЗ(W36;AM36:AZ36;0))
56.	X37	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(X36;$AW$23:$AW$36;0);ПОИСКПОЗ(X36;AM36:AZ36;0))
57.	Y37	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Y36;$AV$23:$AV$36;0);ПОИСКПОЗ(Y36;AM36:AZ36;0))
58.	Z37	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Z36;$AU$23:$AU$36;0);ПОИСКПОЗ(Z36;AM36:AZ36;0))
59.	AA37	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AA36;$AV$23:$AV$36;0);ПОИСКПОЗ(AA36;AM35:AZ35;0))
60.	AB37	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AB36;$AU$23:$AU$36;0);ПОИСКПОЗ(AB36;AM35:AZ35;0))
61.	AC37	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AC36;$AV$23:$AV$36;0);ПОИСКПОЗ(AC36;AM34:AZ34;0))
62.	AD37	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AD36;$AU$23:$AU$36;0);ПОИСКПОЗ(AD36;AM34:AZ34;0))
Девятая строка
63.	W39	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(W38;$AV$23:$AV$36;0);ПОИСКПОЗ(W38;AM33:AZ33;0))
64.	X39	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(X38;$AU$23:$AU$36;0);ПОИСКПОЗ(X38;AM33:AZ33;0))
65.	Y39	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Y38;$AV$23:$AV$36;0);ПОИСКПОЗ(Y38;AM32:AZ32;0))
66.	Z39	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Z38;$AU$23:$AU$36;0);ПОИСКПОЗ(Z38;AM32:AZ32;0))
67.	AA39	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AA38;$AV$23:$AV$36;0);ПОИСКПОЗ(AA38;AM31:AZ31;0))
68.	AB39	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AB38;$AU$23:$AU$36;0);ПОИСКПОЗ(AB38;AM31:AZ31;0))
69.	AC39	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AC38;$AV$23:$AV$36;0);ПОИСКПОЗ(AC38;AM30:AZ30;0))
70.	AD39	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AD38;$AU$23:$AU$36;0);ПОИСКПОЗ(AD38;AM30:AZ30;0))
Десятая строка
71.	W41	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(W40;$AV$23:$AV$36;0);ПОИСКПОЗ(W40;AM29:AZ29;0))
72.	X41	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(X40;$AU$23:$AU$36;0);ПОИСКПОЗ(X40;AM29:AZ29;0))
73.	Y41	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Y40;$AV$23:$AV$36;0);ПОИСКПОЗ(Y40;AM28:AZ28;0))
74.	Z41	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Z40;$AU$23:$AU$36;0);ПОИСКПОЗ(Z40;AM28:AZ28;0))
75.	AA41	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AA40;$AV$23:$AV$36;0);ПОИСКПОЗ(AA40;AM27:AZ27;0))
76.	AB41	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AB40;$AU$23:$AU$36;0);ПОИСКПОЗ(AB40;AM27:AZ27;0))
77.	AC41	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AC40;$AV$23:$AV$36;0);ПОИСКПОЗ(AC40;AM26:AZ26;0))
78.	AD41	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AD40;$AU$23:$AU$36;0);ПОИСКПОЗ(AD40;AM26:AZ26;0))
Одиннадцатая строка (для итогового варианта, рис. 17)
79.	W43	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(W42;$AV$23:$AV$36;0);ПОИСКПОЗ(W42;AM25:AZ25;0))
80.	X43	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(X42;$AU$23:$AU$36;0);ПОИСКПОЗ(X42;AM25:AZ25;0))
81.	Y43	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Y42;$AV$23:$AV$36;0);ПОИСКПОЗ(Y42;AM24:AZ24;0))
82.	Z43	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(Z42;$AU$23:$AU$36;0);ПОИСКПОЗ(Z42;AM24:AZ24;0))
83.	AA43	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AA42;$AV$23:$AV$36;0);ПОИСКПОЗ(AA42;AM23:AZ23;0))
84.	AB43	=ИНДЕКС($E$23:$R$36;ПОИСКПОЗ(AB42;$AU$23:$AU$36;0);ПОИСКПОЗ(AB42;AM23:AZ23;0))

Как уже было упомянуто ранее, данный код полностью не совпадает с байтовым режимом и с кодовой комбинацией Таблицы ДА.3 ГОСТ. Но так как альтернативных режимов в ГОСТ просто больше нет (а числовой и алфавитно-цифровой не подходят), будем и далее использовать алгоритм декодирования последовательности бит на примере байтового режима. Начинаем разбирать секреты первого типа бесплатных библиотек сети Интернет (пример использования библиотеки).

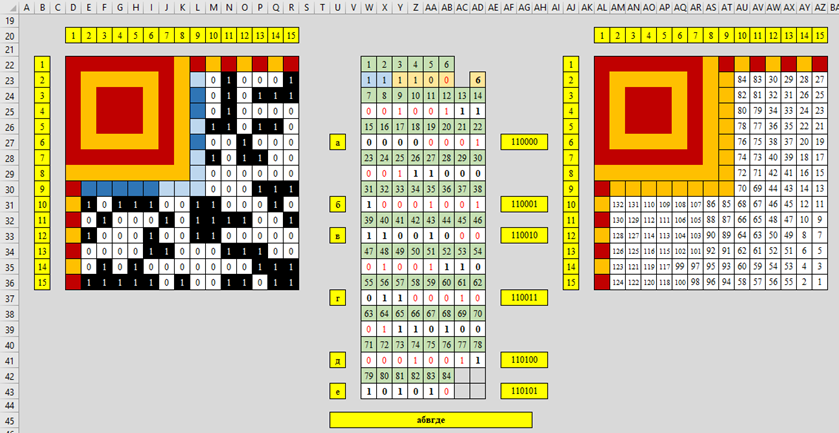
В диапазоне ячеек W23:X23 указан код 11 – обозначает наличие режим Кандзи (таблица 2 ГОСТ). Т.е. для программистов моделистов Ассоциации что кириллица (Россия), что кандзи (Япония, китайская письменность) – одно и то же. Достойное начало. Разбираем дальше. Следующий диапазон из 4-х бит в ячейках Y23:AB23 – диапазон, отображающий битовую комбинацию – 1100 или число 12 (по количеству искомых в микрокоде символов, умноженных на 2). Получается, что для данного режима должен использоваться полный аналог дополнительных кодовых комбинаций, как и в универсальной кодовой системе (например, UTF-8). Но, в UTF-8 используются 8-битовые комбинации, в UTF-16 – 16-битовые комбинации и т.д. Здесь явно просматривается кодовая последовательность короче. Возвращаемся к критериям основателя последовательностей кодирования при шифровании с возможностью нахождения ошибки – кодам Ричарда Хэмминга. Краткий обзор функции определения мощности искусственного алфавита (в данном случае кириллицы) дает мощность порядка 6 бит. Следовательно, первая буква искусственного алфавита будет 000000 или другая аналогичная комбинация. Находим первую последовательность из шести нулей, получаем диапазон AC25:Z27. Уже хорошо, значит с кодом первой буквы А угадали. Осталось определить кодовый индикатор. Здесь проще. Диапазон AA27:Y29 и будет индикатором – 0001001 (тот самый секрет программистов моделистов Ассоциации). Почему выбрано именно число 9 – есть только одно предположение. UNICODE содержит 8 групп кодовых таблиц кириллицы (буквы славянских алфавитов кодировки ISO 8859-5, но перемещённые вверх на 864 позиции; исторические буквы и символы из старославянского (церковнославянского) алфавита; дополнительные буквы для разных языков, использующих кириллицу; старые формы представления кириллических букв; церковнославянские буквотитлы; дополнительные буквы и символы для церковнославянского языка; дополнительные буквы для старой абхазской орфографии; над- и подстрочные буквы-модификаторы). Скорее всего программисты моделисты решили придумать очередной девятый стандарт для своих целей, шутники. Если проверить дальше по коду последовательности, то получим полный скрытый (абсолютно не по ГОСТ) алфавит.

Возвращаемся к первой букве алфавита А, если не учесть бит ячейки AB23, то получаем неполный индикатор 001001, исправляем данный недочет. Итак, первый индикатор будет СЦЕП(AB23;W25:AB25). При этом индикатор количества символов сокращается на один разряд, результат – 110 или 6 в десятичной системе (что полностью соответствует количеству кодовых символов). Следующая буква Б алфавита будет СЦЕП(Z29:AD29;W31) или последовательность 000001, затем индикатор. Третья буква В – СЦЕП(W33:AB33) или последовательность 000010. Буква Г – СЦЕП(AB35:AD35;W37:Y37) или 000011, буква Д – СЦЕП(Y39:AD39) или 000100, и буква Е – СЦЕП(AD41;W43:AA43) или 000101. Как и следовало ожидать, просматривается последовательность порядковых номеров букв алфавита кириллицы от 0 до 32. Код буквы Я – 100000. Итак, первые два секрета программистов моделистов раскрыты. На данном моменте можно остановиться, но интерес в полной автоматизации процесса. Поэтому доведем алгоритм до завершения и перейдем к буквам малого регистра первого типа библиотек.

Автоматизируем процесс перевода последовательности бит из двоичной системы в десятичную:

1.    В ячейку AD23 добавим функцию:

=ДЕС(СЦЕП(Y23:AA23);2)

2.    Получим искомые группы пар символов по шесть бит искусственного алфавита. Добавим функции в ячейки, согласно следующие таблице:

Создадим новый алфавит (не по ГОСТ) на странице Code. Пример полученного результата представлен на рисунке 19.

В ячейка G2 функция:

=ДЕС.В.ДВ(H2;6)

Далее функцию просто за магический квадрат растягиваем до 32 буквы алфавита. Результат представлен на рисунке 19. Возвращаемся на страницу M3 АБВГДЕ.

1.    Сравниваем полученные числовые значения со значениями на странице Code:

2.    Объединим ячейки в одну U45:AG45. В полученную ячейку U45 добавим объединенный посимвольный результат:

=СЦЕП(U27;U31;U33;U37;U41;U43)

3.    На данном этапе можно остановиться, остальное поле занимает код Рида-Соломона. В более сложном алгоритме «Пишем микрокод» будет расшифрован данный этап детально на примере.

Примечание: в данной комбинации (индикатор из семи бит + код символа из шести бит) больше шести символов в М3 занести просто нельзя. Будет переход на класс выше – М4.

 Этап 4. Применение полученного алгоритма для M3 абвгде

 Так как заготовлена битовая последовательность для M3 абвгде заранее, а основной алгоритм очень схож (необходимо будет поменять только маску и функцию комбинации итогового кода), то воспользуемся данным обстоятельством и просто продублируем страницу М3 АБВГДЕ на M3 абвгде с учетом замены исходного микрокода.

Копируем диапазон ячеек T4:AZ16 на странице М3 АБВГДЕ, переходим на страницу M3 абвгде. Выбираем ячейку T4, добавляем скопированный фрагмент T4:AZ16 получаем новый анализ служебной информации (рис. 20).

Для M3 абвгде служебная информация не дублирует служебную информацию для М3 АБВГД. Необходимо использовать маску – 11.

Переходим ко второй составляющей – анализ рабочей области микрокода. Результат представлен на рисунке 21.

Аналогично предыдущему этапу, в диапазоне ячеек W23:X23 указан код 11 – обозначает наличие режима Кандзи (таблица 2 ГОСТ). Следующий диапазон из трех бит в ячейках Y23:AA23 – диапазон, отображающий битовую комбинацию – 110 или число 6 (по количеству искомых в микрокоде символов). Проверка в ячейке AD23 подтверждает полученное значение.

Итак, получены новые кодовые комбинации для букв кириллицы малого регистра. Буква а – 110000, буква б – 110001, в – 110010, г – 110011, д – 110110 и е – 110101. Т.е., малые буквы начинаются с числа 48 в десятичном эквиваленте (третий секрет раскрыт). Создадим новые значения на странице Code (рис. 22).

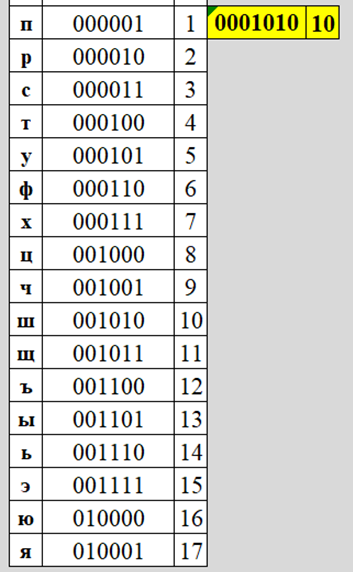
Как можно заметить, выделенный диапазон на 6 разрядов с индикатором 0001001 закончился на букве о. Программисты моделисты, недолго думая, просто добавили очередной индикатор 0001010 и запустили счетчик по второму кругу – гении, что тут сказать… (и четвертый секрет тоже раскрыт).

Сравниваем полученные числовые значения со значениями на странице Code:

В результате получаем полное совпадение кодовой составляющей.

Так как второй тип библиотек (рис. 8) предполагает существенные изменения в алгоритме, то принято решение описать процесс декодирования с абсолютно другим искусственным алфавитом в другой публикации.

 P.S.: как уже стало понятно из описания этапов, реализованное в библиотеке кодирование микрокодов никак не представлено в стандартах. Следовательно, данный алгоритм, как и для других режимов, – ноу-хау программиста или программистов моделистов программного модуля Ассоциации. Согласно ГОСТ, необходимо использовать Таблицу ДА.3 и байтовый режим.

 Удачи в декодировании байтовых последовательностей
Micro QR Code версии M3!!!