В предыдущих статьях статья 1, статья 2, статья 3 мы рассмотрели основные подводные камни автоматизации и анализу АБ тестов, привели подробный обзор статей по этой теме, а так же рассмотрели типичные задачи аналитика данных. В контексте АБ-тестов одним из ключевых аспектов является механизм разделения на группы, который в терминологии специалистов часто называется сплитовалкой.

Может показаться, что задача элементарная - сгенерировать случайное целое число каждому пользователю с вероятностью 1/n, где n - число групп в АБ тесте. Но на практике, особенно для высоконагруженных сервисов, таких как Ozon, возникает множество архитектурных и платформенных сложностей. В данной статье мы сконцентрируемся на основных принципах деления на группы, принятых в индустрии.

Не случайный рандом

Часто деление на группы работает следующий образом - клиентам случайно присваивается значение группы. От присвоенного значения он попадает в control или treatment. Это сопряжено со следующими проблемами:

• Если один и тот же клиент дважды попадет в систему деления на группы, то ему могут быть назначены разные значения групп. В итоге пользователь либо увидит ошибку, либо две разные версии приложения сразу. Такое так же возможно для распределенных систем, если разные запросы пользователя попадут на разные узлы.

• Разделение на группы можно проводить в разные моменты времени. Например до регистрации деление может происходить на основе ip адреса, тогда часть пользователей определятся в одну группу из-за сервиса VPN или особенности работы провайдера выдающего один ip на несколько клиентов. В итоге это приведет к нечестному делению на группы.

• Правило “1 клиент - 1 тест” слишком сильно ограничивает количество одновременно идущих тестов из-за конечного трафика.

• При проведении параллельно нескольких тестов на одних и тех же пользователях нужно быть уверенным, что участники одного теста равномерно распределятся в группах другого теста. Если распределение не равномерно, то получатся искаженные результаты

• Отсутствие отдельно выделенной группы для измерения совокупности нескольких изменений может приводить к проблемам, когда несколько последовательных удачных изменений приводят в целом к неудачным результатам. Например отправка отдельных сообщений пользователям может нести пользу, а три подряд идущих удачных сообщения просто приведут к отключению нотификаций.

• Важно контролировать версии платформы и те её части, на изменение которых направлен тест, чтобы не допускать запуск конфликтующих тестов на одних и тех же пользователях.

• При запуске каждого АБ теста нужно проверять работоспособность функционала командами QA, разработки и аналитики, это должно быть удобно и заранее предусмотрено. Ручная подмена id в базе данных не удобна и приводит к ошибкам.

Рассмотрим далее хорошо зарекомендовавший себя подход к решению этих проблем.

Солим пользователей правильно

Проблемы с неравномерным делением на группы чаще всего решаются с помощью грамотного применения псевдослучайных хэш-функций. Возникает вопрос, каких? Cо стороны команды разработки обычно есть следующие ограничения:

• хэш-функция должна быть реализована в стандартной библиотеке

• хэш-функция должна обладать необходимыми свойствами равномерного распределения

• вычисление группы на основе хэш-функции не замедляет работу сервисов

Заметим, что требование криптографической стойкости не столь актуально, поэтому, например ebay применяет md5. Неудачным примером можно назвать Fowler-Noll-Vo. На практике хорошо себя показывает sha1, SHA-3, Jenkins hash или murmur3.

Но любой hash функции нужно подавать аргумент - randomization unit. Плохой пример - session_id, либо любой другой не устойчивый идентификатор, который может меняться для одного и того же пользователя в зависимости от времени и устройства, которым он пользуется (например hardware_id, маркетинговые id атрибуции). Этому вопросу посвящен раздел в известной книге. Чаще всего user_id полученный пользователем после регистрации является наиболее надежным аргументом для хэш-функции.

Разделим всех пользователей на слоты (бакеты) с помощью остатка от деления хэш-функции и назначим каждому слоту тритмент группу определенного теста, либо контрольную группу.

group_id = MD5hash(user_id + salt) % n_groups

здесь n_groups - количество групп в АБ-тесте, salt - некоторая фиксированная строка, не позволяющая пользователям угадывать свою группу на основе user_id.

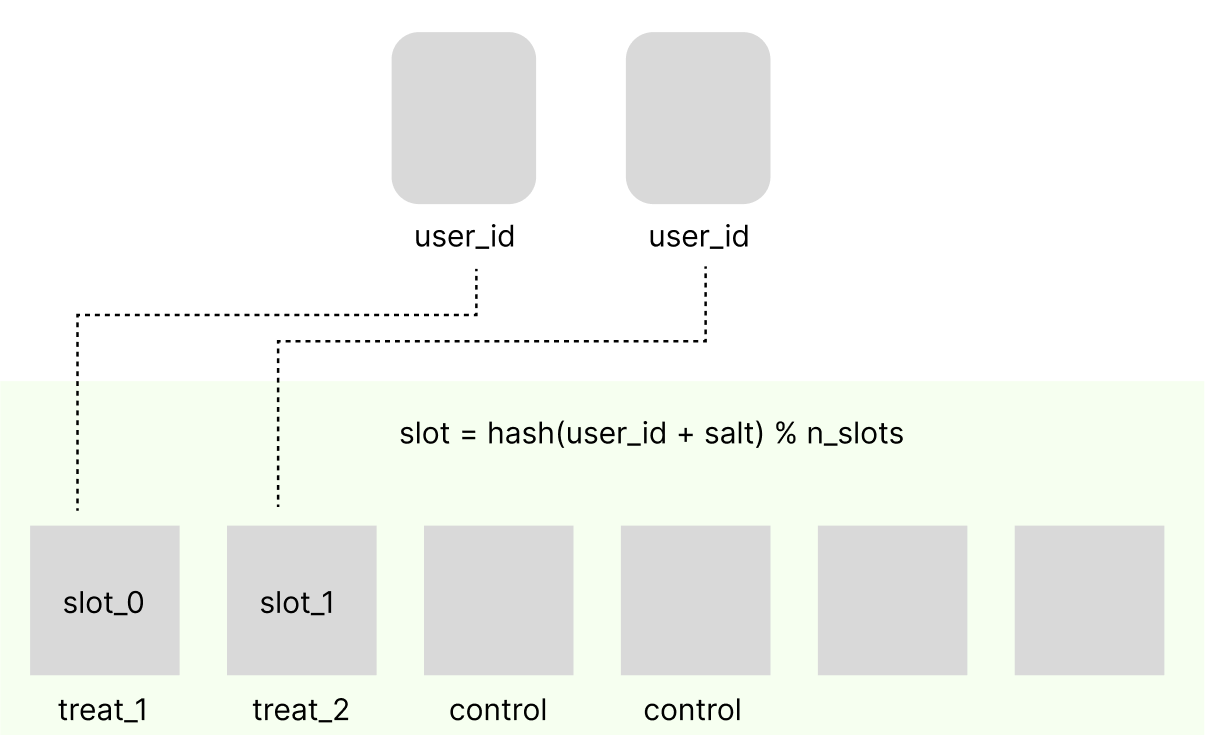
Чтобы решить проблему итогового эффекта от последовательного введения нескольких небольших изменений можно добавить выделенные слоты hold-out. Так же выделенные слоты для QA и команды разработки решают проблему ручного добавления пользователей в тестовые группы

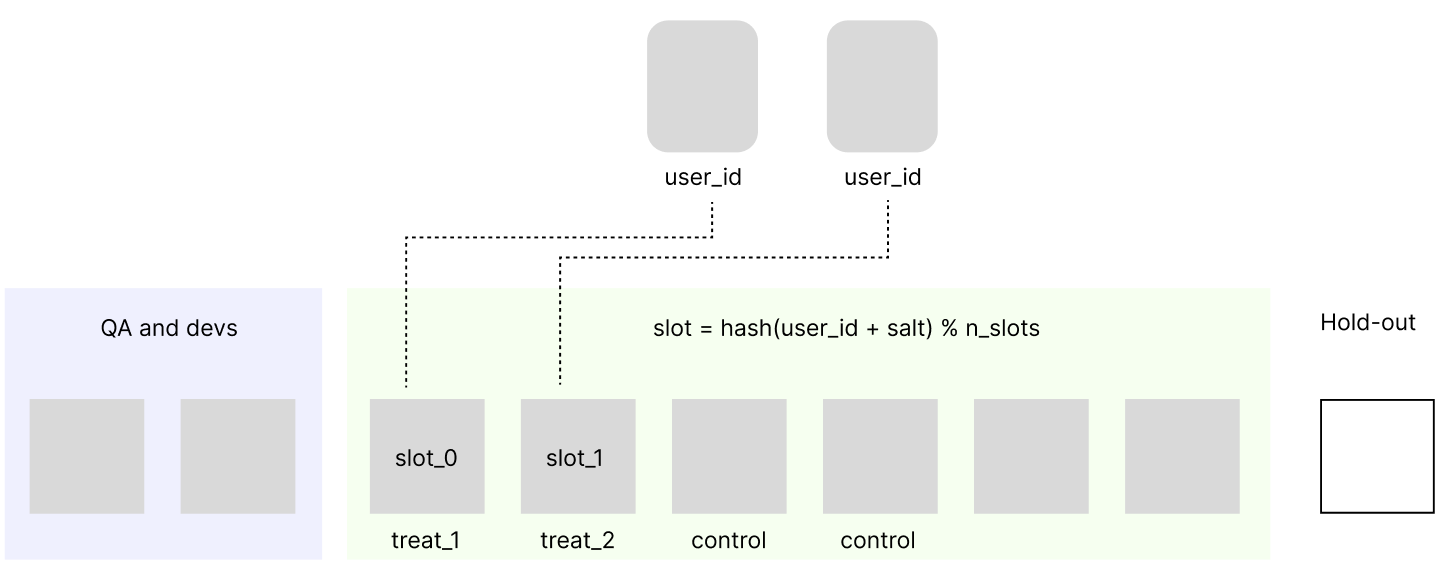
Но пока не решена другая серьезная проблема - при таком подходе аудитория остаточно быстро закончится, потому что для статистически значимого сравнения часто необходима большая выборка, а долгое время ожидания не допустимо. Разные страницы сайта и разные разделы приложения можно проверять на одних и тех же пользователях без боязни пересечений. Практика Microsoft показывает, что проблема взаимодействия тестов часто переоценена, и участие одного и того же пользователя в нескольких тестах скорее предпочтительно, что так же подтверждается опытом Statsig и Facebook. Для каждого теста можно создать новые слоты с независимым от других тестов распределением изменив в формуле соль (salt → layer_id + salt).

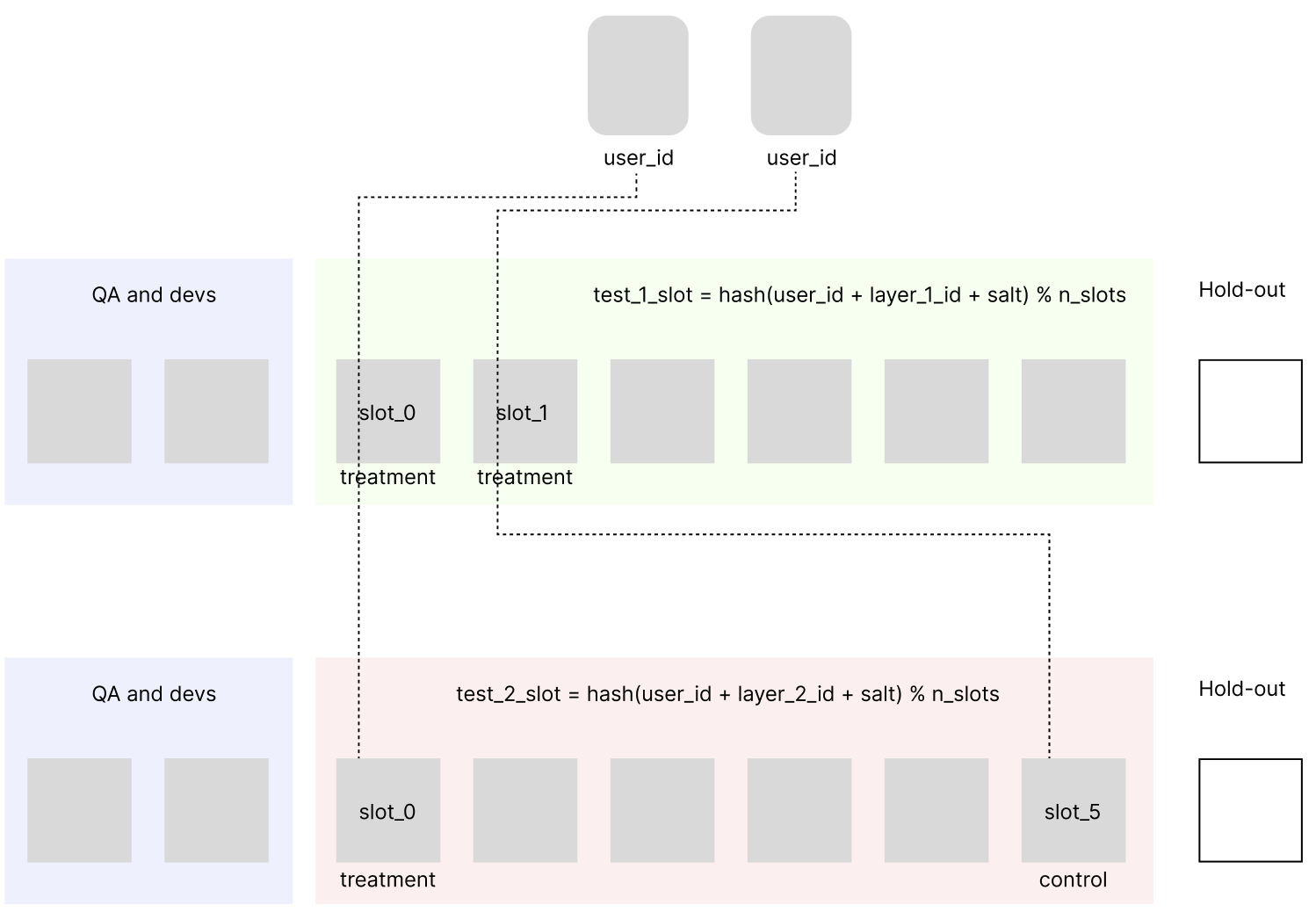
Количество слотов можно менять для каждого теста в отдельности, оставляя возможность делить пользователей на нужное количество групп. Кроме того, добавление параметра layer_id позволяет создать новый тест с ровно тем же распределением пользователей, что и в предыдущем, “приклеив” новый тест к существующему.

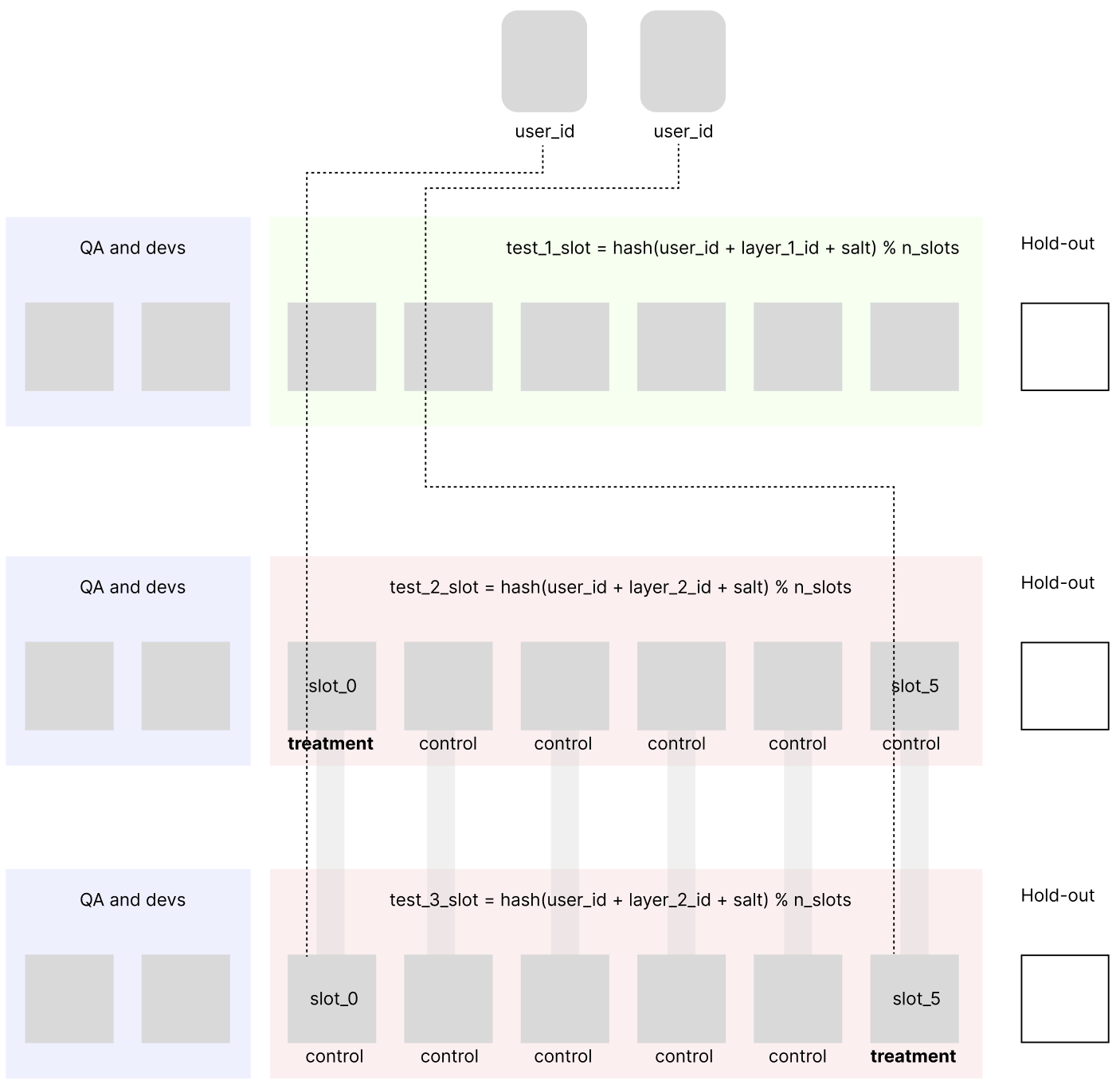
Это может быть полезно, если достоверно известно, что два теста нельзя пересекать по аудитории. Для контроля за пересечением можно внедрить систему взаимоисключающих тегов, так чтобы нельзя было создать два теста с разными layer_id и заведомо пересекающейся функциональностью.

Типичным требованием так же бывает таргетинг - тест должен действовать только на пользователей определенной платформы, страны, или бизнеса. Не подходящие под фильтр пользователя не попадают в тест

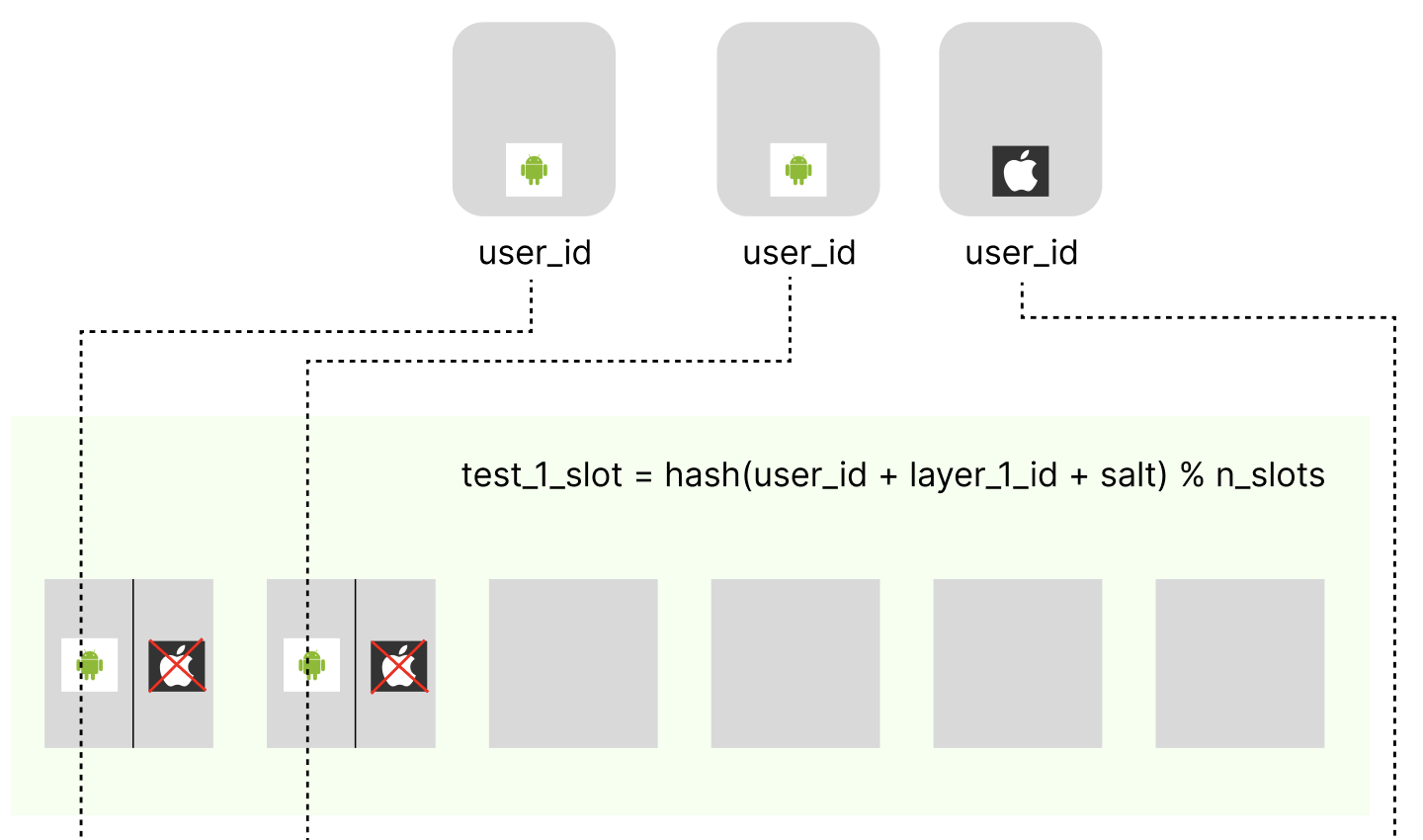
Применять таргетинг и одинаковый layer_id для разных тестов нужно с осторожностью. Результаты анализа такого АБ-теста в общем случае нельзя экстраполировать на всех пользователей. Кроме того, сужение аудитории увеличивает время проведения теста и снижает чувствительность.

Описанная архитектура базируется на основном предположении о равномерности распределения пользователей по слотам. Но при использовании псевдослучайной хеш-функции слоты практически всегда будут отличаться по количеству пользователей. Кроме того, если пользователи выяснили, что они попадают в тест и перерегистрируются, то дисбаланс слотов может стать существенным. Как следить за тем, что эта разница не велика? Приведем далее идеи и куски кода, которые помогут решить эту проблему.

Проверка  Split Sample Ratio Mismatch (SSRM)

Для начала сгенерируем синтетические данные для миллиона последовательных user_id начиная с 0. Значение layer_id будет равно “test_layer_X”, где X - случайное число,  salt = "salt_2024", а количество слотов 12.

import numpy as np
from spookyhash import hash128
from scipy.stats import chi2
from tqdm import trange

n_users = 10**6
n_slots = 12
salt = "salt_2024"


def split_users_to_slots(
    user_ids: np.ndarray, n_slots: int, layer_id: str, salt: str
) -> np.ndarray:
    slot_counts = np.zeros(n_slots, dtype=np.int64)
    for user_id in user_ids:
        hash_argument = str(user_id) + layer_id + salt
        slot_id = hash128(hash_argument.encode("utf-8")) % n_slots
        slot_counts[slot_id] += 1
    return slot_counts


def gen_random_slot_counts(n_users: int, n_slots: int, salt: str) -> np.ndarray:
    user_ids = np.arange(n_users, dtype=np.int64)
    layer_id = "layer_test_" + str(np.random.choice(1000))
    slot_counts = split_users_to_slots(user_ids, n_slots, layer_id, salt)
    return slot_counts

В качестве хэш-функции будем использовать spookyhash V2. Функция gen_random_slot_counts возвращает numpy массив из 12 чисел, соответствующих количеству пользователей в каждом слоте.

Для проверки равномерности будем использовать критерии хи-квадрат и PSI_k

def srm_chi_2(slot_counts: np.ndarray, alpha: float = 0.05) -> bool:
    n_slots = slot_counts.size
    n_samples = slot_counts.sum()
    expected_counts = np.full(n_slots, n_samples / n_slots)
    chi2_stat = ((slot_counts - expected_counts) ** 2 / expected_counts).sum()
    p_value = 1 - chi2.cdf(chi2_stat, n_slots - 1)
    return 1 if p_value < alpha else 0


def srm_psi_k(slot_counts: np.ndarray, alpha: float = 0.05, k: int = 2) -> bool:
    n_slots = slot_counts.size
    n_samples = slot_counts.sum()
    psi_k_stat = (
        (slot_counts / n_samples - 1 / n_slots)
        * (np.log(slot_counts / n_samples) - np.log(1 / n_slots))
    ).sum()
    chi2_alpha_quantile = chi2.ppf(1 - alpha, n_slots - 1)
    return 1 if psi_k_stat > (k + 1) / k / n_samples * chi2_alpha_quantile else 0

Нам понадобятся две величины - процент ложных срабатываний теста и чувствительность к дисбалансам. Для первой проверки прогоним сто раз с случайным layer_id и посчитаем в каком проценте увидим срабатывание проверок

def srm_false_ratio(
    check_func: callable, n_users: int, n_slots: int, salt: str, n_checks: int = 100
) -> None:
    false_positive_count = 0
    for _ in trange(n_checks):
        slot_counts = gen_random_slot_counts(n_users, n_slots, salt)
        false_positive_count += check_func(slot_counts)

    return false_positive_count / n_checks

Для проверки чувствительности искусственно добавим в 0 слот некоторый процент пользователей, который будем постепенно увеличивать. В конце вычислим среднее значение дисбаланса, на котором происходит первое срабатывание.

def add_srm(slot_counts: np.ndarray, ratio: float) -> np.ndarray:
    slot_counts[0] += int(slot_counts[0] * ratio)
    return slot_counts  

def srm_sensivity(
    check_func: callable,
    n_users: int,
    n_slots: int,
    salt: str,
    n_checks: int = 20,
    srm_increment: float = 0.001,
    max_srm: float = 0.1,
) -> None:
    log = np.zeros(n_checks)
    for i_check in trange(n_checks):
        slot_counts = gen_random_slot_counts(n_users, n_slots, salt)
        srm = 0
        while srm <= max_srm:
            slot_counts = add_srm(slot_counts, srm_increment)
            srm += srm_increment
            if check_func(slot_counts):
                break
        log[i_check] = srm
    return log.mean(), log.std()

import numpy as np
from spookyhash import hash128
from scipy.stats import chi2
from tqdm import trange

n_users = 10**6
n_slots = 12
salt = "salt_2024"


def split_users_to_slots(
    user_ids: np.ndarray, n_slots: int, layer_id: str, salt: str
) -> np.ndarray:
    slot_counts = np.zeros(n_slots, dtype=np.int64)
    for user_id in user_ids:
        hash_argument = str(user_id) + layer_id + salt
        slot_id = hash128(hash_argument.encode("utf-8")) % n_slots
        slot_counts[slot_id] += 1
    return slot_counts


def gen_random_slot_counts(n_users: int, n_slots: int, salt: str) -> np.ndarray:
    user_ids = np.arange(n_users, dtype=np.int64)
    layer_id = "layer_test_" + str(np.random.choice(1000))
    slot_counts = split_users_to_slots(user_ids, n_slots, layer_id, salt)
    return slot_counts


def add_srm(slot_counts: np.ndarray, ratio: float) -> np.ndarray:
    slot_counts[0] += int(slot_counts[0] * ratio)
    return slot_counts


def srm_chi_2(slot_counts: np.ndarray, alpha: float = 0.05) -> bool:
    n_slots = slot_counts.size
    n_samples = slot_counts.sum()
    expected_counts = np.full(n_slots, n_samples / n_slots)
    chi2_stat = ((slot_counts - expected_counts) ** 2 / expected_counts).sum()
    p_value = 1 - chi2.cdf(chi2_stat, n_slots - 1)
    return 1 if p_value < alpha else 0


def srm_psi_k(slot_counts: np.ndarray, alpha: float = 0.05, k: int = 2) -> bool:
    n_slots = slot_counts.size
    n_samples = slot_counts.sum()
    psi_k_stat = (
        (slot_counts / n_samples - 1 / n_slots)
        * (np.log(slot_counts / n_samples) - np.log(1 / n_slots))
    ).sum()
    chi2_alpha_quantile = chi2.ppf(1 - alpha, n_slots - 1)
    return 1 if psi_k_stat > (k + 1) / k / n_samples * chi2_alpha_quantile else 0


def srm_false_ratio(
    check_func: callable, n_users: int, n_slots: int, salt: str, n_checks: int = 100
) -> None:
    false_positive_count = 0
    for _ in trange(n_checks):
        slot_counts = gen_random_slot_counts(n_users, n_slots, salt)
        false_positive_count += check_func(slot_counts)

    return false_positive_count / n_checks


def srm_sensivity(
    check_func: callable,
    n_users: int,
    n_slots: int,
    salt: str,
    n_checks: int = 20,
    srm_increment: float = 0.001,
    max_srm: float = 0.1,
) -> None:
    log = np.zeros(n_checks)
    for i_check in trange(n_checks):
        slot_counts = gen_random_slot_counts(n_users, n_slots, salt)
        srm = 0
        while srm <= max_srm:
            slot_counts = add_srm(slot_counts, srm_increment)
            srm += srm_increment
            if check_func(slot_counts):
                break
        log[i_check] = srm
    return log.mean(), log.std()


chi_2_false_srm = srm_false_ratio(srm_chi_2, n_users, n_slots, salt)
psi_k_false_srm = srm_false_ratio(srm_psi_k, n_users, n_slots, salt)
print(f"SRM false positive for chi2: {chi_2_false_srm:.5f}")
print(f"SRM false positive for psi_k: {psi_k_false_srm:.5f}")

chi_2_sens = srm_sensivity(srm_chi_2, n_users, n_slots, salt)
psi_k_sens = srm_sensivity(srm_psi_k, n_users, n_slots, salt)
print(f"Mean SRM sensivity for chi2: {chi_2_sens[0]:.5f}, std = {chi_2_sens[1]:.5f}")
print(f"Mean SRM sensivity for psi_k: {psi_k_sens[0]:.5f}, std = {psi_k_sens[1]:.5f}")

Результат:

SRM false positive for chi2: 0.06

SRM false positive for psi_k: 0.00

Mean SRM sensivity for chi2: 0.01170, std = 0.00497 Mean

SRM sensivity for psi_k: 0.01555, std = 0.00399

Тест PSI_2 обладает меньшей чувствительностью, но меньшим количеством ложных срабатываний. Оба метода хорошо подходят для контроля распределений и должны применяться на постоянной основе для мониторинга здоровья тестов. Неравномерное распределение это индикатор проблем на которые обязательно необходимо обращать внимание перед подсчетом результатов АБ теста.

Плавное внедрение и мониторинг

Такой подход содержит в себе важную дополнительную функциональность - можно запускать любую новую функциональность как АБ-тест на 100 слотов, первый из которых treatment с новой функциональностью, а остальные контрольные. Далее, следя за метриками в дэшбордах или выделенной внутренней системе можно постепенно наращивать количество treatment слотов. Автоматические системы оповещения (alerting) позволят остановить распространение ошибок и откатиться к предыдущей версии. В английской литературе это называется ramp up deployment, canary, continuous integration.

Практика безопасного плавного внедрения может оказаться эффективной приманкой, позволяющей убедить соседние команды начать активнее применять АБ тесты, как один из наиболее надежных и эффективных методов анализа и оценки развития продукта.

Заключение

В этой статье мы касались только проблемы неравномерности количества пользователей в слотах (группах). Но нужно следить и за равномерностью других параметров (ковариат) в каждом слоте, например количество перерегистраций (дублей), распределение стран, и так далее. Для этого так же можно применять тесты семейства хи-квадрат, тесты на сравнение распределений (Колмогорова-Смирнова, Лиллиефорса, Андерсона - Дарлинга), основанные на эконометрических критерии PSI_k и другие. Кроме того, если о пользователях уже известна какая-то информация и собраны метрики, то более эффективным и чувствительным будет подход мэтчинга, парной стратификации или повторной рандомизации. Идея этих подходов состоит в том, чтобы детерменированно разделить пользователей на группы так, чтобы они были максимально похожими друг на друга, заранее позаботившись о выбросах. Проверка близости может так же проводиться обозначенными выше статистическими критериями.

Авторы

Marat Yuldashev

Anastasia Zaremba

Mikhail Tretyakov