Пока люди с вычислительными машинами в пустую тратят время на перебор гиперпарамтеров нейронок внутри библиотек Scikit-learn – настоящие гении тайм-менеджмента выбирают TPE и Optuna. 

В этой статье мы рассмотрим самые популярные методы оптимизации Grid.Search и Random.Search, принципы Байесовской/вероятностной оптимизации, а также TPE. В конце прописали небольшой словарик с функциями, атрибутами и объектами фреймворка, а также привели наглядный пример использования. 

Оптимизация гиперпараметров – основа для нейронки: Grid.Search и Random.Search

Гиперпараметры — это "большие" настройки, критерии, по которым определяется структура модели и способ ее обучения. Сравнить можно с той же кастомизацией персонажа, где уклон ползунка в "толстое телосложение" растягивает сотни полигонов на персонаже, прямоугольников из которых он состоит, и совершенно меняет его облик. Поэтому они и называются гипер-параметрами, глобальными, определяющими всю систему и конечный результат ее работы. 

Для машинного обучения подбор параметров — подготовка фундамента, от которого и будет выстраиваться нейронка. Гиперпараметры определяют степень обученности и переобученности модели. Они выставляются до обучения, пока "параметры" или веса/коэффиценты — результаты внутренней работы нейронки и определяются в процессе ее работы. 

Но если по-научному, оптимизация гиперпараметров — нахождение кортежа, при котором бы модель минимизировала заранее функцию потерь / loss funtion независимых данных: среднеквадратичную ошибку, коэффициент детерминации в регрессии или, например, кросс-энтропию в классификации. Ну и другие функции. 

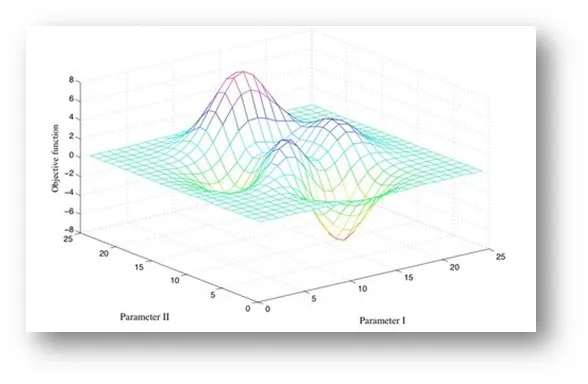
Оптимизация — это такая своеобразная примочка к самому обучению, дополнительная фаза обучения. Метрику производительности/целевую функцию можно визуализировать как тепловую карту или поверхность в n+1 мерном пространстве. Как на картинке выше. 

Ну и соответственно, чем неровнее, непостояннее поверхность — тем сложнее отыскать нужные нам гиперпараметры. 

Гиперпараметрами и могут быть сами функции активации, применяемые к каждому нейрону функции или число эпох/проходов (Number of epochs) через набор данных. Для случайного леса: число деревьев, объектов на листе, признаков для разбиения дерева. 

Под каждую архитектуру идет свой набор гиперпараметров. 

Важно подобрать такую комбинацию, чтобы мы получили на выходе адекватный результат и при этом не потратили все электричество в районе, сжарив нашу рендер-ферму из 50 видеокарт. 

В библиотеке Scikit-learn используется два метода генерации подборки гиперпараметров: GridSearch и RandomSearch.

GridSearch – самый проверенный, но "тупой" способ поиска гиперпараметров

Метод перебора — для каждого гиперпараметра подбирается набор значений, которыми обучается модель и оценивается на основе валидационных данных. Вы получите на выходе идеальный вариант, но придется, мягко говоря, подождать. 

Представим простую инструкцию по поиску гиперпараметров “серчем” в рандомизированном дереве. 

Нам нужно два параметра: количество деревьев в лесу (n_estimators) и максимальная глубина каждого дерева (max_depth). 

Мы определяем набор возможных значений для каждого из этих гиперпараметров: n_estimators = [50, 100, 200] и max_depth = [10, 20, 30]. 

Затем GridSearch составляет сетку всех возможных комбинаций этих значений (например, [(50, 10), (50, 20), (50, 30), (100, 10), ..., (200, 30)]). 

Для каждой комбинации гиперпараметров модель случайного леса обучается на обучающем наборе данных, а затем оценивается ее производительность с использованием набора валидации или кросс-валидации. 

Выбирается лучшая комбинация по цифрам. Например, если модель с параметрами в 100 деревьев, максимальной глубиной в 20 уровней дает наилучшую производительность — гиперпараметры выбираются как оптимальные. Максимум качества и максимум затрат по времени. 

Другим оптимальным вариантом будет Random.Search. Название говорит само за себя — рандомный подбор комбинаций, в котором можно потерять наилучшие варианты под нейронку. Но оптимальные находятся за приемлемый промежуток времени. 

Импортируется import RandomizedSearchCV

После выборки сетки параметров, например, для того же рандомизированного дерева и инициализации, мы создаем объект:

random_search = RandomizedSearchCV (estimator=model, param_distributions=param_grid, n_iter=100, cv=5, verbose=2, random_state=42, n_jobs=-1)

Внутри самого рандом-серча обозначается модель, сетка, количество итераций и фолдов для кросс-валидации, verbose или количество получаемой информации в процессе работы алгоритма. 

С другой стороны, как бы принцип работы с поиском по сетке не казался вам "исчерпывающим", зачастую рандомный подход выгоднее. Подробно о преимуществах рассказывают James Bergstra и Youshua Bengio в своей работе. Вариант для тех, кто работает с большим числом параметров или высокой размерностью сетки. 

Дело то в том, что не все гиперпараметры так уж и важны для обучения модели и функции потерь, поэтому шансы попасть в нужные точки зачастую высоки. 

Визуализацию мы взяли из статьи выше. 

Во втором случае “попаданий” значительно больше, нежели в примере с перебором по сетке. 

Вот и все "самые" популярные методы работы с гиперпараметрами. Но мы уже заметили, что представляют они из себя — два конца одной палки. Все они предлагают достаточно костыльные методы подбора гиперпараметров. Отслеживать эффективность перебора значений — вот, что нам нужно. И так как подбор гиперпараметров — штука вероятностная и прогнозирует оптимальное направление поиска подходящих комбинация значений, она нам и подходит для быстрого подбора параметров

И сегодня речь идет про фреймворк, который поможет оптимизировать вашу модель по максимуму и не потратить несколько часов на "парсинг" оптимального набора значений. 

Байесовская статистика: вероятностный подход в оптимизации модели

Математика предоставляет нам один механизм предугадывания. Если есть данные уже после перебора парочки комбинаций — они могут дать информацию о том, куда лучше двигаться в последующем переборе, какую часть сетки выбрать и получить оптимальные наборы гиперпараметров быстрее. Вот тут то и нам поможет байесовский способ оптимизации. 

Достаточно предрассчитывать степень неопределенности и предполагаемой структуры зависимости между гиперпараметрами и "целевой" функцией, чтобы приблизиться к нужным значениям. 

Мы пользуемся результатами в каждой итерации точности предсказания и получаем конечный, адекватный результат. 

Задача Байесовской оптимизации — найти целевую функцию. 

Хорошим сравнением с методом Байеса может быть интерполяция. Предположим, что часть графика у нас не определены, нам даны лишь некоторые значения — мы стремимся зашить неопределенность и восстановить график/функцию. Как если бы по стоянкам автомобиля и его промежуточным остановкам пытались восстановить путь, а точнее вероятность того, что он поехал так, а не иначе. 

Но здесь мы стремимся прояснить зависимость между гиперпараметрами и целевой функцией, например, функцией потерь или метрикой и исследовать пространство,  используя  информацию о предыдущих оценках целевой функции и дальше выводить последующий набор гиперпараметров. 

Для начала строится априорная вероятностная модель, где описывается первоначальное представление о связи между гиперпараметрами и целевой функцией. Чем больше данных об оценках целевой функции мы получаем, тем лучше наше знание о пространстве гиперпараметров и его зависимости от целевой функции. 

Грубо говоря, байесовский метод оптимизации – модернизированный рандомный поиск. 

Это позволяет нам более точно выбирать следующие наборы гиперпараметров для оценки и тем самым улучшать процесс оптимизации. К счастью, математики тут не так много. 

Формула для выбора следующей точки в байесовской оптимизации:

Функция улучшения [improvement(x)] обычно определяется как разница между текущим лучшим значением целевой функции и прогнозируемым значением целевой функции для данной точки x:

improvement(x)=max(0,best_value−predicted_value(x))

где: best_value – лучшее значение целевой функции, найденное на данный момент, а predicted_value(x) – прогнозируемое значение целевой функции для точки

Таким образом, байесовская оптимизация выбирает следующую точку для оценки, максимизируя ожидаемое улучшение целевой функции. Этот подход позволяет эффективно исследовать пространство гиперпараметров, уделяя больше внимания областям, где ожидается наибольшее улучшение, и избегая областей с низким потенциалом улучшения.

Возникает классическая дилемма: разведка или продвижение? Стоит ли проводить еще одну итерацию, чтобы получить больше информации или нам ее достаточно для определения оптимальных гиперпараметров?

Самым простым методом тут выступает метод Sequential Model-Based Optimization, где вероятностная суррогатная модель обучается по полученным данным из целевой функции, а функция выбора по предсказательному распределению суррогатной модели оценивает насколько полезно дальше проводить разведку вообще нужных нам точек... То самое Esploration против Exploation, получение новой информации или использование старой. 

Помните мы говорили, что оптимизация гиперпараметров — примочка к обучению модели? Байесовская оптимизация стремится сделать ее минимально вычислительно затратной, минимизировать ее размер. 

На основе этого метода оптимизации появляется достаточно много и других методов, но для нас самый главный подход – TPE, который используется в Optuna.  

Он отличается лишь применением дополнительного парзеновского окна, где вычисляется “плотность” вероятностей, из-за чего достигается еще большая точность предсказаний качественных гиперпараметров. 

Отличие от байесовского подхода при моделировании апостериорного распределения вероятностей для гиперпараметров используется парзеновское окно оценивания работает как метод аппроксимации (приближения) к нужным данным. Двигаясь по итерациям, разведываниям точек мы выясняем, где находится больше “оптимальных” значений. 

В начале процесса оптимизации TPE строится априорная модель — распределение вероятностей для каждого гиперпараметра в их пространстве. Вот тут и подключается парзеновское оценивание, которое аппроксимирует распределение на основе предыдущих оценок целевой функции.

Далее, априорное распределение разбивается на две части: одна часть соответствует "успешным" оценкам целевой функции (т.е. наборам гиперпараметров, которые дали хорошие результаты), а другая часть – "неуспешным" оценкам (наборам гиперпараметров, которые дали плохие результаты).

Далее вытесняются неуспешные гиперпараметры и поиск как бы директируется, т.е выбирается направление дальнейшего подбора – к нему применяется функция распределения вероятностей. С каким шансом этот набор гиперпараметров обретет успех? 

Через несколько итераций мы находим вполне оптимальный набор гиперпараметров и запускаем обучаться нашу нейронку. 

Optuna или Based-фреймворк для сторонников быстрого подбора гиперпараметров

Сегодня TPE применяется как раз таки в Optuna, а так как процесс оптимизации избежать никак нельзя — многие из пользователей постепенно переходят на этот фреймворк. 

Как же с ним работать? В фреймворке предусмотрены не только TPE и привычные Random/Grid Search, но и "методы" поиска гиперпараметров по принципам генетических алгоритмов, которые упоминать в этой статье мы не будем. 

Ограничимся предустановленным TPE, которого вполне хватит для работы с большинством нейронок. Давайте разберем, как работать с TPE в Optuna, ведь все приходят во фреймворк именно за этим методом. После того как прочитаете нашу статью – загляните обязательно документацию. 

Она слегка замудрена, поэтому ниже мы приведем хотя бы частичный словарь функций и объектов фреймворка. 

create_study: Создает объект Study для оптимизации гиперпараметров.

study.optimize: Запускает процесс оптимизации гиперпараметров.

study.best_params: Возвращает лучшие найденные гиперпараметры.

study.best_value: Возвращает лучшее найденное значение метрики.

study.trials: Возвращает список всех проб в рамках оптимизационного исследования.

study.enqueue_trial: Добавляет пробу в список проб, но не выполняет ее сразу.

study.remove_trial: Удаляет пробу из списка проб.

study.trial: Получает пробу по ее идентификатору.

study.trial_callbacks: Устанавливает обратные вызовы, вызываемые перед началом и после завершения пробы.

study.set_user_attr: Устанавливает пользовательский атрибут Study.

study.user_attrs: Возвращает словарь пользовательских атрибутов Study.

study.load: Загружает состояние Study из базы данных.

study.save: Сохраняет состояние Study в базе данных.

delete_study: Удаляет объект Study и все его данные.

delete_all_study: Удаляет все исследования из базы данных.

delete_trials: Удаляет пробы из базы данных.

create_trial: Создает пробу и добавляет ее в базу данных.

enable_pruning: Включает механизм обрезки (pruning) проб в Study.

disable_pruning: Отключает механизм обрезки проб в Study.

get_pruned_trials: Возвращает пробы, которые были обрезаны (pruned).

delete_pruned_trials: Удаляет пробы, которые были обрезаны (pruned), из базы данных.

study_name_exists: Проверяет, существует ли исследование с заданным именем.

get_storage: Получает объект хранилища, используемый объектом Study.

Ну и, конечно же, список объектов, зашитых внутрь фреймворка. 

1. Study – оптимизированное исследование. Он содержит информацию о пробах, их результатах и используемых стратегиях оптимизации. У него есть парочка своих атрибутов и метод:

   optimize(func, n_trials, ...) –  метод для запуска оптимизации с определенным числом проб.

   best_params – атрибут, содержащий лучшие найденные гиперпараметры.

   best_value – атрибут, содержащий лучшее найденное значение метрики.

   trials – атрибут, содержащий список всех проб в рамках оптимизационного исследования.

2. Trial – “попытка” оптимизации. Он предоставляет методы для выбора значений гиперпараметров и регистрации результатов. Четыре ключевых метода.

   suggest_categorical(name, choices) – метод для выбора категориального значения.

   suggest_uniform(name, low, high) – Метод для выбора значения из равномерного распределения.

  suggest_loguniform(name, low, high) – метод для выбора значения из логнормального распределения.

   report(value, step) – метод для регистрации результатов пробы.

3. Sampler – настройка самого подбора гиперпараметров. Выбирает  какие комбинации гиперпараметров будут протестированы на каждой итерации. 

   RandomSampler – Случайное сэмплирование.

   TPESampler – Стратегия TPE.

   GridSampler –  Сэмплирование сетки.

Да, это те самые методики рандомизированного перебора, по сетке и технологии TPE. Для нас релевантен именно второй вариант. 

4. Объект FrozenTrial – замороженная попытка с информацией после итерации. Он используется для анализа и визуализации результатов после завершения оптимизации.

5. StudySummary – описание исследования. Представляет собой краткое описание исследования, содержащее его основные характеристики, такие как количество проб, использованные стратегии и т. д.

6. StudyDirection Перечисление, определяющее направление оптимизации (минимизация или максимизация).

7. Summary – резюме ресерча.  Представляет собой краткое описание исследования, содержащее его основные характеристики, такие как количество проб, использованные стратегии и т. д.

8. TrialState – мониторинг попытки. Определяет состояние пробы (например, проба в процессе выполнения, завершена или обрезана).

Да, фреймворк не такой уж и сложный и работает практически автоматизированно, хотя зачастую предлагает оптимальные решения в два раза быстрее в сравнении с тем же Grid или Random Search. 

Оптимизируем нейронку на живом примере

На микроуровне оптимизация простая. Сначала необходимо импортировать библиотеку Optuna:

import optuna

Далее определяете функцию, которую хотите оптимизировать. 

def objective(trial): # Определение гиперпараметров для оптимизации 
  param1 = trial.suggest_float('param1', 0.0, 1.0) 
  param2 = trial.suggest_int('param2', 1, 100)  
  
  # Оценка производительности модели с использованием выбранных гиперпараметров 
  score = evaluate_model(param1, param2)  
  return score

Запуск оптимизации: После определения функции цели вы можете запустить процесс оптимизации с использованием TPE в Optuna:

study = optuna.create_study(direction='maximize', sampler=optuna.samplers.TPESampler())
study.optimize(objective, n_trials=100)

Здесь direction='maximize' указывает, что мы стремимся максимизировать оценку производительности модели, а n_trials=100 определяет количество итераций оптимизации. 

Пропишем отдельно выводы оптимизации на экран. 

print('Best parameters:', study.best_params)
print('Best score:', study.best_value)

Это позволит вам узнать лучшие гиперпараметры, найденные в результате оптимизации, и сразу оценку производительности. 

Функция create_study() создает объект исследования, в котором выполняется процесс оптимизации. С помощью функции optimize() можно запустить процесс оптимизации для заданной функции цели. 

Результаты оптимизации, включая лучшие гиперпараметры и значения функции цели, доступны через методы объекта исследования, такие как study.best_params и study.best_value. 

Класс Trial представляет собой отдельную итерацию оптимизации и предоставляет методы для предложения различных типов значений гиперпараметров. 

Отдельные итерации оптимизации доступны через объект исследования с помощью атрибута study.trials. 

Попробуем проделать все эти действия на примере конкретной модели

Импортируем библиотеки для нашей нейронки и, конечно, Optuna. 

import optunafrom sklearn.model_selection 
import train_test_splitfrom sklearn.ensemble 
import RandomForestClassifierfrom sklearn.metrics 
import accuracy_score

Optuna – для оптимизации, функции train_test_split – для разделения данных, класс RandomForestClassifier из библиотеки scikit-learn – для создания модели рандомизированного леса, и accuracy_score – для оценки производительности модели.

Определим функцию оценки:

def objective(trial): 
# Загружаем нужные нам данные 
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)  

# Выбираем оптимизируемые параметры 
n_estimators = trial.suggest_int('n_estimators', 10, 100) 
max_depth = trial.suggest_int('max_depth', 2, 32)  

# Обучаем модель 
model = RandomForestClassifier(n_estimators=n_estimators, 
                               max_depth=max_depth) model.fit(X_train, y_train)  

# Проводим валидационную оценку 
val_preds = model.predict(X_val) accuracy = accuracy_score(y_val, val_preds)  

return accuracy

Это функция objective, которую мы хотим оптимизировать. Она на входе принимает объект trial, который используется для выбора значений гиперпараметров.

Функция загружает данные, определяет гиперпараметры (количество деревьев и максимальная глубина), обучает модель RandomForestClassifier и возвращает точность модели на валидационном наборе данных.

Создадим нужный нам объект Study с методом оптимизации TPE:

study = optuna.create_study(direction='maximize', 
sampler=optuna.samplers.TPESampler())

Здесь мы создаем объект Study с указанием стратегии оптимизации 'maximize' для максимизации целевой метрики (accuracy) и используем TPESampler для использования стратегии оптимизации TPE.

Запускаем оптимизацию!

study.optimize(objective, n_trials=100)

Этот код запускает процесс оптимизации методом optimize(). Мы передаем функцию objective в качестве аргумента, которая будет оптимизироваться, и указываем количество проб/попыток (n_trials), которые Optuna должен провести.

Подводим итоги. 

best_params = study.best_params
best_accuracy = study.best_value

Получаем гиперпараметры для нашего леса и их точность на валидационных данных с атрибутами best_params и best_value объекта Study. 

Напоминаем, что у ребят есть своя документация, где прописан весь словарь и применимость фреймворка для моделей, почитайте перед тем как использовать.