Рассуждение о природе «замороженной случайности» в распределении простых чисел / forpes.ru

Главная
Рассуждение о природе «замороженной случайности» в распределении простых чисел

Рассуждение о природе «замороженной случайности» в распределении простых чисел

18.04.2024 09:06

saaivs 2 3400 Источник

Гипотеза о природе сложности

Недавно в ленте FB попалось интереснейшее видео Теория Всего и феноменологическая Теория Сложности. Что это и почему это важно? где, помимо всего прочего интересного, прозвучала следующая цитата:

Идея самоиндуцированных спиновых стекол состоит в том, что беспорядок, в общем-то, не нужен, а что нужно нужно то, что называется фрустрации, или то, что называется конкурирующее взаимодействие. То есть когда у вас на систему действует несколько разнонаправленных тенденций и каждая хочет систему упорядочить, но каждая хочет систему упорядочить по-своему. Когда они все присутствуют одновременно и действуют одновременно система не может выбрать куда ей упорядочиваться. И вот она приходит в это в это состояние спинового стекла, несмотря на то что никакого беспорядка нет.

Михаил Кацнельсон, (c)

(Примечание: Спиновые стёкла рассматриваются как состояние магнитной системы со случайным распределением спин-спиновых взаимодействий. В системе отсутствует дальний порядок, причем беспорядок в системе замороженный, то есть не меняется со временем).

Я достаточно далёк от физики в целом и данной тематики в частности, но вот сам тезис о связи конкурирующих взаимодействий и свойствах сложных систем демонстрировать, с одной стороны квазислучайное поведение, а с другой определённые закономерности показался очень любопытным, поскольку вызвал ассоциации с совершенно неожиданным объектом для сравнения - простыми числами. Точнее с их распределением.

В этой связи приведу другой тезис, который буду использовать как вторую отправную точку:

Ни нули дзета-функции Римана, ни собственные значения гауссовой случайной эрмитовой матрицы не похожи на случайно разбросанные точки (отличаются от идеально случайного разброса);

С одной стороны, распределение простых чисел выглядит вполне случайным (хотя, право, мало ли что как выглядит...!?!), с другой стороны - случайность тут тоже "замороженная", ну а с третьей - присутствуют и закономерности.

В частности, имеется:

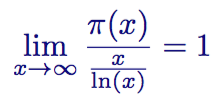
С неё и начнем.

Функция a(x)

Рассмотрим некоторую функцию где $x \in \mathbb{R}$ , такую что точно выполняется соотношение:

$\frac{ \pi(x) }{ (\frac{x}{\log_{a(x)}{x}}) } = 1 \text{ (1)}$

Из (1) выразим :

$x = \pi(x) \cdot \log_{a(x)}{x}$ $\log_{a(x)}{x} = \frac{x}{ \pi(x) }$ $a(x)^{\frac{x}{\pi(x)}} = x$ $(a(x)^{\frac{x}{\pi(x)}})^{\frac{\pi(x)}{x}} = x^{\frac{\pi(x)}{x}}$

Получим :

$a(x) = x^{\frac{\pi(x)}{x}} \text{ (2)}$

Мы определили такую функцию , значения которой есть основания логарифма числа при котором соотношение (1) в точности соответствует распределению простых чисел (т.е. функции $\pi(x)$ ).

Можно заметить, что характерный ступенчатый вид функции естественным образом обусловлен свойствами базовых функций $\pi(x)$ и $a_{k}(x)$ .

(Рис. 3) Функция распределения простых чисел до значения — (Рис. 3) Функция распределения простых чисел $\pi(x)$ до значения

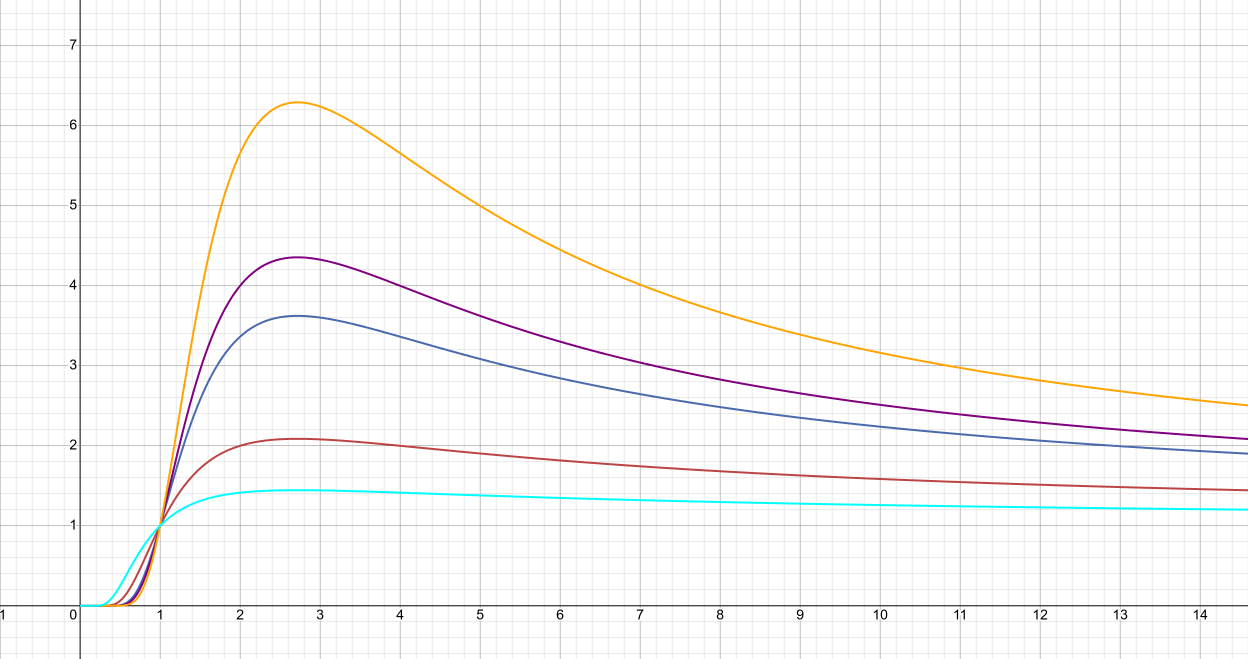
(Рис. 4) Семейство функций вида . — (Рис. 4) Семейство функций вида $a_{k}(x) = x^{\frac{k}{x}}$ $k \in \mathbb{N}$ .

(Рис. 4) Семейство функций вида $a_{k}(x) = x^{\frac{k}{x}}$ $k \in \mathbb{N}$ .

(Рис. 5) Функция $a_{70}(x) = x^{\frac{70}{x}}$

(Рис. 5) Функция $a_{70}(x) = x^{\frac{70}{x}}$

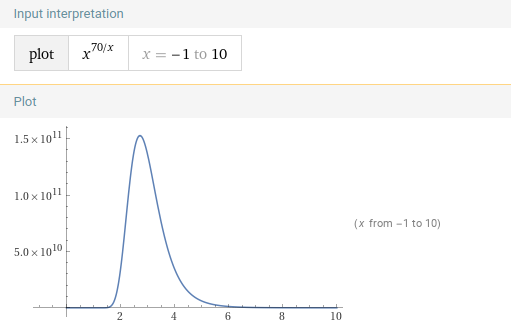
Посмотрим на функции внимательней.

Элементарные свойства функций a_k(x) и π(x)

Семейство функций вида $a_{k}(x) = x^{\frac{k}{x}}$ для $\forall k \in \mathbb{N}$ и $\forall x \in \mathbb{R}$ имеет ряд примечательных свойств:

1.1. $a_{k}(x)$ имеет единственный максимум при равный $e^{\frac{k}{e}}$ и монотонно и достаточно быстро убывает для всех $x \gg e$ .
1.2. $\lim_{x\to +\infty}{a_{k}(x)} \to 1$
1.3. $\forall x>1$ $a_{k+1}(x) > a_{k}(x)$
1.4. $a_{k}(x)$ растёт крайне быстро и до очень больших значений на фиксированном интервале .

Функция $\pi(x)$ обладает следующими элементарными свойствами:
2.1. $0 < \pi(x) < x$
2.2 $0 \leq \pi(x_{i+1}) - \pi(x_{i}) \leq 1$ неубывающая ступенчатая функция.

Интерпретация графика a(x)

Несложно заметить, что функция (Рис. 1) является композицией функций $a_{k}(x)$ (Рис. 4), на интервалах $[p_0,p_1), [p_1,p_2), ...,[p_i,p_{i+1}), [p_{i+1},p_{i+2}), ...$ по всем простым , где $k=\pi(x)$ для $x \in [p_i, p_{i+1})$ .

Поскольку на каждом интервале значение $\pi(x)=const$ , то каждому интервалу соответствует свой ниспадающий участок соответствующей функции $a_{k}(x)$ ("гирлянда").

В силу 1.3 $a_{k+1}(x) > a_{k}(x)$ каждое появление нового простого числа(в силу 2.2) гарантированно поднимает график вверх("вершина гирлянды - простое число") выше предыдущего значения, а каждое последующее в силу 1.1 снова опускает его.

В силу того, что множество простых чисел бесконечно, а в силу 1.1 функция убывает и в то же время в силу 1.2 не опускается ниже 1 мы имеем постоянно действующий процесс взаимно конкурирующих взаимодействий.

Вывод

Согласно базовой гипотезе, наличие этих "фрустраций" (в смысле данном выше), вероятно, и может определять "случайный" характер распределения простых чисел.

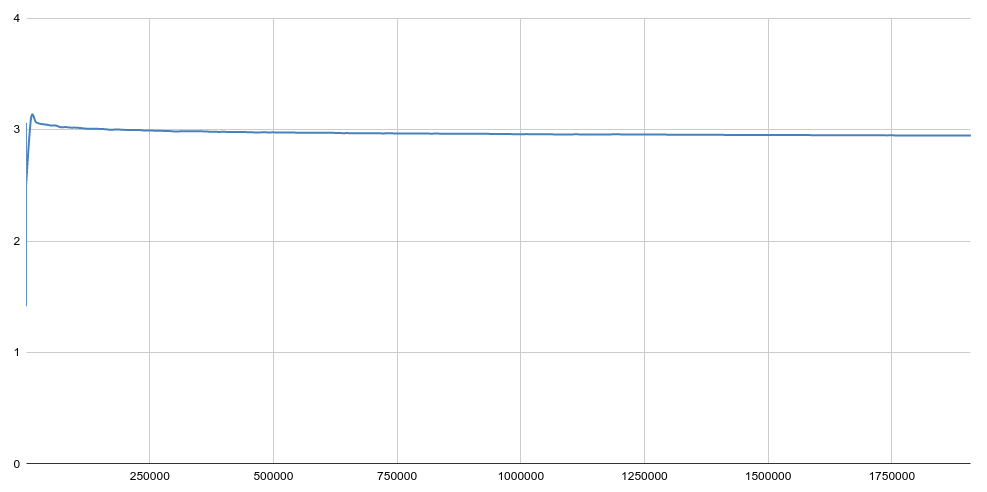
P.S. Предел a(x)

Глядя на Рис. 2 можно предположить, что:

$\lim_{x\to +\infty}{a(x)} \to e$

Во всяком случае, это было бы красиво ~~банально~~ :)

Комментарии (2)

CaptainFlint
18.04.2024 12:31
#26739041
+7
Глядя на Рис. 2 можно предположить, что:
$\lim_{x\to +\infty}{a(x)} \to e$
Во всяком случае, это было бы красиво :)

Мне кажется, это было бы не столько красиво, сколько банально. Ведь в теореме о распределении простых чисел участвует именно натуральный логарифм, так к чему ещё может стремиться функция a(x), являющаяся основанием этого логарифма? Конечно, это требует доказательства, так как я сходу не уверен, что взаимные предельные переходы там обязаны согласовываться, но это был бы самый очевидный и ожидаемый результат.
1. saaivs Автор
  18.04.2024 12:31
  #26741477
  Пожалуй, вы правы.