Аннотация
Статья посвящена систематизации основных положений о случайных и псевдослучайных последовательностях (СП и ПСП) чисел. Дан краткий обзор известных подходов к тестированию на случайность генерируемых последовательностей. Прикладное значение данной тематики определяется тем, что ПСП широко используются в криптографических системах защиты информации для выработки ключевой и вспомогательной информации (случайные числа, векторы инициализации и пр.).

Введение
Изучением случайности с древних времен занимались не только математики. Случайность стала предметом исследования во многих математических дисциплинах – в статистике, в теории игр, теории нечетких множеств, в физике и химии – при изучении свойств микромира, в экономике – при исследовании влияния случайных факторов на зарождение и развитие экономических кризисов, на траектории курсов мировых валют, в истории и социологии – при исследовании значения фактора случайности на развитие исторических событий и на смену эпох. Развитие науки уже в XX веке показало, что цепь случайных поистине непредсказуемых событий приводит исследователя не к хаосу, а к весьма жестким закономерным выводам глобального характера. Этот тезис нетрудно проиллюстрировать с помощью центральной предельной теоремы (и других теорем) теории вероятностей. Следует отметить особенность систем случайных объектов, которая может показаться в определенном смысле парадоксальной. Гораздо чаще можно описать, в крайнем случае, предсказать, глобальные, нежели локальные закономерности больших систем. Это определяет два безусловно востребованных современных направления исследования: поиск глобальных закономерностей случайных систем и обоснование для случайной системы непредсказуемости событий локального характера. Случайные последовательности чисел или элементов других множеств эффективно используются для экспериментального исследования свойств сложных объектов и систем.
Случайные последовательности
СП играют в криптографии важную роль, они используются для формирования ключевых и инициальных параметров криптографических алгоритмов, а также последовательностей шифрующих подстановок в поточных криптосистемах. Случайность и криптография тесно взаимосвязаны: основная цель криптографических систем состоит в преобразовании неслучайных осмысленных открытых текстов в кажущуюся случайной последовательность символов шифрованного текста. Это свойство криптосистем используют для генерации ПСП.
Наилучшие криптографические свойства криптосистемы достигаются при использовании так называемых идеальных случайных последовательностей (ИСП), математическая модель которых представляется реализацией последовательности независимых случайных величин, имеющих равномерное распределение вероятностей на заданном конечном алфавите. Такие последовательности называют также равномерно распределёнными (на некотором конечном множестве) случайными последовательностями (РРСП). Описанию свойств РРСП посвящено множество работ, в частности, [1], [4], [5] и [7].
Подходы к определению термина «случайность»
Существуют различные подходы к формальному определению термина «случайность», основанные на понятиях вычислимости и алгоритмической сложности [2]. Исторически первый подход, частотный, предложен фон Мизесом (Mises) в начале XX века и развивался Черчем (Church), Колмогоровым и Ловеландом (Loveland). Идея частотного подхода в том, что в СП должна наблюдаться устойчивость частот встречаемости элементов. Например, знаки 0 и 1 должны встречаться независимо и с равными вероятностями не только в самой двоичной СП, но и в любой ее подпоследовательности, выбранной независимо от исходных условий генерации.
Другой подход, сложностной, предложенный независимо Колмогоровым и Чейтином (Chaitin), основан на том, что любое описание реализации СП не может быть существенно короче самой этой реализации. То есть СП должна иметь сложное строение, и энтропия ее начальных элементов должна быть велика. При данном подходе показано, что последовательность случайна, если ее алгоритмическая сложность близка к длине последовательности.
Третий подход, количественный, развит Мартин-Лефом (Martin-Lof). Он заключается в разбиении вероятностного пространства последовательностей на неслучайные и случайные (последних относительно много). Неслучайными считаются последовательности, в которых наблюдаются какие-либо закономерности. Последовательность признается случайной, если она проходит набор определенных тестов, предназначенных для выявления закономерностей. Однако если требовать, чтобы последовательность прошла любой статистический тест, то окажется, что СП вообще не существует. На практике используют некоторый набор тестов, где доля СП, им не удовлетворяющих, стремится к 0 при неограниченном увеличении длины последовательностей.
В последние десятилетия в связи с требованиями, возникающими в криптографических приложениях, сформировался криптографический подход к определению СП, где последовательность считается случайной, если вычислительная сложность поиска закономерностей не меньше заданной величины. Этот подход согласован с существующим системным подходом к определению стойкости криптографических систем.
Указанные подходы к определению случайности имеют недостатки. Частотный подход затруднен на практике неопределенностью правил выбора подпоследовательностей, сложностной подход влечет необходимость уменьшения избыточности языка программирования. Использование количественного подхода затруднено определением множества тестов, применяемых к исследуемым последовательностям. Нижние оценки сложности криптографического подхода ориентированы на набор известных тестов, а он со временем может пополняться, что приводит к переоценке сложности. Вместе с тем, для криптографических приложений наиболее подходящим является криптографический подход, учитывающий статистические свойства последовательностей и область их применения.
Тестирование ПСП
Доказано (Herring, C., Palmore, J.I. Random Number Generators are Chaotic, 1995), что любая алгоритмическая реализация последовательности является несовершенной, то есть истинно случайная последовательность не может быть вычислена по какому-то правилу и, следовательно, она должна быть непериодической бесконечной последовательностью. Генерируемые по определенному правилу последовательности, имитирующие РРСП, называются псевдослучайными последовательностями (ПСП). Удачная имитация понимается как близость ряда характеристик генерируемых ПСП к аналогичным характеристикам ИСП.
Порождение ПСП, используемых в криптографических приложениях, основано на реализации многократных итераций определенного преобразования конечного множества Х (часто Х есть множество двоичных n-мерных векторов). Такая выходная последовательность является периодической. Однако длина периода может быть весьма большой, это гарантируется, в частности, использованием линейных регистров сдвига с примитивными характеристическими многочленами. Для многих генераторов ПСП доказаны хорошие статистические свойства и высокая линейная сложность, большая длина периода, однако доказать аналитические и статистические свойства часто не удается. Тогда для обоснования многих свойств используются статистические тесты.
Многообразие критериев оценки ПСП чрезвычайно велико. Каждый из подходов к анализу последовательностей можно отнести к одной из двух групп.
Первая группа связана с поиском закономерностей, позволяющих воспроизвести последовательность по ее отрезку небольшой длины. При этом основные требования к последовательности сводятся к отсутствию в ней относительно простых межзнаковых зависимостей.
Вторая группа критериев связана с оценкой статистических свойств последовательности: имеется ли в исследуемой последовательности какой-либо частотный дисбаланс, позволяющий аналитику прогнозировать по известному отрезку последовательности следующий (предыдущий) знак, то есть предположить значение следующего (предыдущего) бита с вероятностью большей, чем при случайном выборе? Основные требования к ПСП по второй группе критериев сводятся к тому, чтобы ряд ее статистических свойств соответствовал свойствам ИСП, в частности, в ПСП должны быть равномерно распределены частоты встречаемости и отдельных знаков, и s-грамм при достаточно больших значениях s.
При системном подходе для анализа последовательностей используются известные тесты и разрабатываются новые тесты с учётом особенностей анализируемого объекта. Если в ходе анализа в некотором классе последовательностей обнаруживается новая слабость, то разрабатывается соответствующий новый тест, который пополняет используемый набор известных тестов.
Обе группы методов анализа последовательностей составляют системный подход к анализу ПСП, в частности, к разработке поточных шифров.
Одна из первых формулировок основополагающих требований к статистическим свойствам периодических двоичных ПСП была дана С. Голомбом. Эти требования к последовательностям получили известность в криптографии как постулаты Голомба (Golomb S.W. Shift Register Sequences, 1967). Постулаты Голомба приведены, в частности, в монографии [7]. Постулаты исходят из условия сохранения положительных статистических свойств, присущих линейным рекуррентным последовательностям с максимальной длиной периода.
Правила Голомба не гарантируют высокого качества ПСП и являются скорее необходимыми. На практике использование постулатов Голомба для оценки качества ПСП затруднительно, в силу сложности теоретического расчета длин периодов ПСП, частот s–грамм на периоде, а также значений функции автокорреляции. Расчет на ЭВМ возможен лишь для ПСП с небольшой длиной периода, что ограничивает использование постулатов Голомба в криптографических приложениях.
Цель и задачи статистического тестирования ПСП
Тестирование ПСП на случайность – это способ выявления ее определенных свойств с помощью сравнения характеристик ПСП с аналогичными характеристиками ИСП.
С помощью статистического тестирования ПСП решаются следующие задачи:
1) оценка свойств выходной последовательности генератора ПСП с точки зрения использования в криптографическом алгоритме (например, в качестве секретного ключа);
2) оценка качества криптографических примитивов (хэш-функций, блочных и поточных шифров) по их выходным последовательностям, от которых требуется неотличимость от ИСП, в частности, проверка таких криптографических свойств, как лавинный эффект изменения выходных данных алгоритмов при искажениях, корреляция промежуточных и выходных последовательностей;
3) идентификация генераторов ПСП, выдающих «неслучайные» последовательности; разработка новых генераторов ПСП; проверка корректности реализации генераторов ПСП.
Суть тестирования обычно сводится к проверке так называемой «нулевой гипотезы» H0 относительно исследуемой последовательности x(k)=(x_1,…,x_k) длины k, согласно которой x получена на основе k независимых испытаний вероятностной схемы с равномерным распределением.
Вообще статистический тест Т есть двузначная функция
 ,
,
где A* – множество последовательностей в алфавите А. Статистический тест Т разделяет множество V(k) последовательностей длины k на множество V(k,0) «неслучайных» последовательностей (как правило, относительно небольшое) и множество V(k,1)=V(k)/V(k,0) случайных последовательностей. Вероятность P того, что тест отвергает случайно выбранную двоичную последовательность x(k), равна V(k,0)/2^k. Как правило, в реальных тестах P не превышает 0,01.
Сложность точного вычисления функции Т велика ввиду громоздкости области определения. Поэтому статистическое тестирование для принятия/отклонения гипотезы H0 выполняется с помощью статистики f_T, то есть относительно просто вычислимой функции, отображающей множество последовательностей во множество действительных чисел, и вероятностного распределения статистики для гипотезы H0, определяемого теоретико-вероятностными методами. Статистический тест – это совокупность статистики, вычисленной по исходным данным, и решающего правила, в соответствии с которым по значению статистики определяют, принять или отклонить гипотезу H0.
Статистический тест является вероятностным, то есть возникают ошибки двух родов, являющиеся важными характеристиками теста:
1) ошибка a первого рода, если последовательность случайна, но H0 отклоняется;
2) ошибка b второго рода, если последовательность не случайна, но H0 принимается.
Решение о прохождении последовательности статистического теста принимается на основе различных критериев [7].
На основе порогового значения. Подход основан на вычислении для данной последовательности x(k) статистики теста f_T(x(k)) и её последующем сравнении с некоторым пороговым значением c(k). В соответствии с критерием двоичная последовательность x(k) не проходит статистический тест, если f_T(x(k))<c(k). Такой подход дает ошибочные решения относительно часто и считается не вполне надежным.
На основе фиксированного доверительного интервала. При данном подходе последовательность x(k) не проходит статистический тест, если f_T(x(k)) находится вне пределов доверительного интервала значений статистики, вычисленного для заданного уровня значимости a. При меньших уровнях значимости ширина доверительного интервала больше. Данный критерий более надежный по сравнению с первым.
На основе вычисления p-value. Третий класс критериев опирается на вычисление характеристики теста из сегмента [0,1], называемой p-значением (p-value). Статистика теста, рассматриваемая как случайная величина с известным законом распределения, строится так, чтобы большие значения указывали на некий дефект случайности последовательности. Значение вероятности p-value есть вероятность того, статистика теста примет значение большее, чем наблюдаемое при опыте в предположении случайности последовательности. То есть малые значения p-value соответствуют неслучайности последовательности. Решающее правило: при уровне значимости a последовательность x(k) не проходит статистический тест, если p-value<a. Значения a следует брать из интервала [10^(-3);10^(-2)]. Преимущество данного подхода по сравнению с прежними в том, что единожды рассчитанную вероятность p-value сравнивают с любым выбранным уровнем значимости без дополнительных расчетов.
Таким образом, основные этапы тестирования ПСП таковы:
1. формулировка гипотезы Н0 случайности последовательности;
2. задание уровня значимости a (вероятности ошибки 1-го рода), обычно a берется из интервала [10^(-3);10^(-2)];
3. вычисление значения статистики f_T(x(k)) для исследуемой последовательности x(k);
4. вычисление p-value из интервала (0;1) по формуле, зависящей от конкретного теста;
5. сравнение p-value со значением a: если p-value >a, то тест пройден.
Существующие инструменты для статистического тестирования ПСП
Для выявления закономерностей к анализируемым ПСП (а также к их отрезкам различной длины) применяется широкий спектр различных статистических тестов. В последние десятилетия разработано большое количество тестов для анализа ПСП. Приведем известные наборы статистических тестов:
1. 11 тестов: Donald Knuth (Stanford University), The Art Of Computer Programming Vol. 2 Seminumerical Algorithms, www-cs-faculty.stanford.edu/~uno/taocp.html
2. 15 тестов: Andrew Rukhin, et. al. (NIST ITL), NIST Statistical Test Suite, csrc.nist.gov/groups/ST/toolkit/rng/documentation_software.html
3. 12 тестов: George Marsaglia (Florida State University), DIEHARD, stat.fsu.edu/pub/diehard
4. 11 тестов: Pierre L’Ecuyer, Richard Simard (Departement d’Informatique et de Recherche Operationnelle Universite de Montreal), TestU01, www.iro.umontreal.ca/~simardr/testu01/tu01.html
5. 5 тестов: Helen Gustafson, et. al.(Queensland University of Technology), Crypt-XS, коммерческая версия, www.qut.edu.au/institute-for-future-environments
Существуют другие описания и реализации статистических тестов, во многом повторяющие тесты из представленных выше наборов:
1. Alfred Menezes и др., Handbook of Applied Cryptography
2. Peter Hellekalek (University of Salzburg), The pLab Project, random.mat.sbg.ac.at
3. John Walker (Autodesk, Inc.), ENT, www.fourmilab.ch/random
4. Robert G. Brown (Duke University), Dieharder, www.phy.duke.edu/~rgb/General/dieharder.php
5. George Marsaglia (Florida State University), Wai Wan Tsang (The University of Hong Kong), «Distilled» version of Diehard, www.jstatsoft.org/v07/i03
Несмотря на немалое количество существующих реализаций статистических тестов ПСП, данное направление постоянно развивается, и в настоящее время активно появляются новые проекты, которые предлагают новые реализации рассмотренных тестов, в том числе, в условиях распределенных вычислительных систем.
Рассмотренные наборы статистических тестов ПСП составляют удобный и гибкий инструмент исследования генераторов ПСП, применяемых в криптографических приложениях.
Пакет NIST STS обладает большей гибкостью, расширяемостью и эффективностью (с точки зрения временных затрат на осуществление тестирования) и является наиболее полным из имеющихся пакетов для статистического тестирования двоичных последовательностей (подробнее можно посмотреть в работах [5], [8], [9]). Тесты пакета NIST STS подробно рассмотрены в статье «Статистические проверки случайных чисел методами NIST» habrahabr.ru/company/securitycode/blog/237695 [3]. На основе пакета NIST STS могут быть построены методики более полного статистического и структурного анализа последовательностей, учитывая то, что для надежной оценки качества ПСП, выработанной генератором, целесообразно проводить не одно, а несколько испытаний.
Все тесты направлены на выявление различных дефектов случайности. Подробнее о выявляемых дефектах случайности можно посмотреть в работе [8].
На практике принятие или отвержение нулевой гипотезы основывают на результатах применения нескольких независимых тестов. Когда независимые тесты приводят к различным выводам, используется комбинирование результатов тестов с помощью статистик, учитывающих совокупность результатов всех использованных тестов. При небольшом количестве комбинируемых тестов используется статистика Фишера-Пирсона, которая сравнивается с распределением хи-квадрат. Если количество комбинируемых тестов велико, то рекомендуется применение теста Колмогорова-Смирнова.
В таблице 1 даны некоторые тесты, рекомендуемые для тестирования ПСП различных длин.
Таблица 1. Статистические тесты для ПСП различных длин
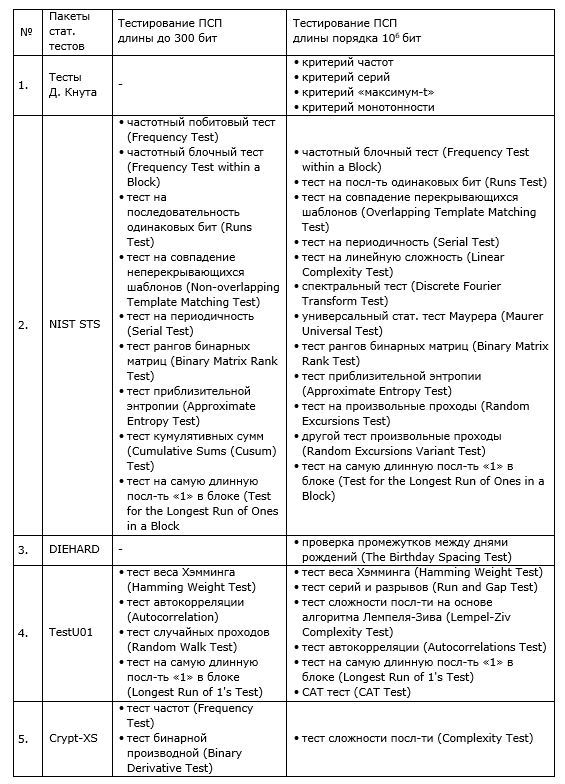
Предварительный анализ рассмотренных статистических тестов позволил определить, какие из них наиболее пригодны для использования в различных задачах разработки средств криптографической защиты информации.
Список использованной литературы
1. Агибалов Г.П. Избранные теоремы начального курса криптографии. Учебное пособие. Томск: Изд-во НТЛ, 2005. – 116 с.
2. Архангельская А.В. Построение высокоскоростных квантовых генераторов случайных чисел для систем защиты информации. Диссертация на соискание ученой степени кандидата технических наук, Москва, 2008. – 182 с.
3. Блог Кода Безопасности: Статистические проверки случайных чисел методами NIST. – habrahabr.ru/company/securitycode/blog/237695
4. Варфоломеев А.А., Жуков А.Е., Пудовкина М.А. Поточные криптосистемы. Основные свойства и методы анализа стойкости. Учебное пособие, М.: ПАИМС, 2000. – 272 с.
5. Вильданов Р.Р., Мещеряков Р.В., Бондарчук С.С. Тесты псевдослучайных последовательностей и реализующее их программное средство // Математическое обоснование и теоретические аспекты информационной безопасности. – www.tusur.ru/filearchive/reports-magazine/2012-25-2/108.pdf
6. Потий А.В., Орлова С.Ю., Гриненко Т.А. Статистическое тестирование генераторов случайных и псевдослучайных чисел с использованием набора статистических тестов NIST STS.
7. Фомичев В.М. Методы дискретной математики в криптологии, М.: Диалог-МИФИ, 2010. – 424с.
8. Rukhin, A., Soto, J., Nechvatal, J., Smid, M., Barker, E., Leigh, S., Levenson, M., Van- gel, M., Banks, D., Heckert, A., Dray, J., Vo, S. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. – www.csrc.nist.gov/publications/nistpubs/800-22/sp-800-22-051501.pdf.
9. Soto Juan, Statistical Testing of Random Number Generators, National Institute of Standards & Technology. – csrc.nist.gov/groups/ST/toolkit/rng/documents/nissc-paper.pdf
Статья посвящена систематизации основных положений о случайных и псевдослучайных последовательностях (СП и ПСП) чисел. Дан краткий обзор известных подходов к тестированию на случайность генерируемых последовательностей. Прикладное значение данной тематики определяется тем, что ПСП широко используются в криптографических системах защиты информации для выработки ключевой и вспомогательной информации (случайные числа, векторы инициализации и пр.).

Введение
Изучением случайности с древних времен занимались не только математики. Случайность стала предметом исследования во многих математических дисциплинах – в статистике, в теории игр, теории нечетких множеств, в физике и химии – при изучении свойств микромира, в экономике – при исследовании влияния случайных факторов на зарождение и развитие экономических кризисов, на траектории курсов мировых валют, в истории и социологии – при исследовании значения фактора случайности на развитие исторических событий и на смену эпох. Развитие науки уже в XX веке показало, что цепь случайных поистине непредсказуемых событий приводит исследователя не к хаосу, а к весьма жестким закономерным выводам глобального характера. Этот тезис нетрудно проиллюстрировать с помощью центральной предельной теоремы (и других теорем) теории вероятностей. Следует отметить особенность систем случайных объектов, которая может показаться в определенном смысле парадоксальной. Гораздо чаще можно описать, в крайнем случае, предсказать, глобальные, нежели локальные закономерности больших систем. Это определяет два безусловно востребованных современных направления исследования: поиск глобальных закономерностей случайных систем и обоснование для случайной системы непредсказуемости событий локального характера. Случайные последовательности чисел или элементов других множеств эффективно используются для экспериментального исследования свойств сложных объектов и систем.
Случайные последовательности
СП играют в криптографии важную роль, они используются для формирования ключевых и инициальных параметров криптографических алгоритмов, а также последовательностей шифрующих подстановок в поточных криптосистемах. Случайность и криптография тесно взаимосвязаны: основная цель криптографических систем состоит в преобразовании неслучайных осмысленных открытых текстов в кажущуюся случайной последовательность символов шифрованного текста. Это свойство криптосистем используют для генерации ПСП.
Наилучшие криптографические свойства криптосистемы достигаются при использовании так называемых идеальных случайных последовательностей (ИСП), математическая модель которых представляется реализацией последовательности независимых случайных величин, имеющих равномерное распределение вероятностей на заданном конечном алфавите. Такие последовательности называют также равномерно распределёнными (на некотором конечном множестве) случайными последовательностями (РРСП). Описанию свойств РРСП посвящено множество работ, в частности, [1], [4], [5] и [7].
Подходы к определению термина «случайность»
Существуют различные подходы к формальному определению термина «случайность», основанные на понятиях вычислимости и алгоритмической сложности [2]. Исторически первый подход, частотный, предложен фон Мизесом (Mises) в начале XX века и развивался Черчем (Church), Колмогоровым и Ловеландом (Loveland). Идея частотного подхода в том, что в СП должна наблюдаться устойчивость частот встречаемости элементов. Например, знаки 0 и 1 должны встречаться независимо и с равными вероятностями не только в самой двоичной СП, но и в любой ее подпоследовательности, выбранной независимо от исходных условий генерации.
Другой подход, сложностной, предложенный независимо Колмогоровым и Чейтином (Chaitin), основан на том, что любое описание реализации СП не может быть существенно короче самой этой реализации. То есть СП должна иметь сложное строение, и энтропия ее начальных элементов должна быть велика. При данном подходе показано, что последовательность случайна, если ее алгоритмическая сложность близка к длине последовательности.
Третий подход, количественный, развит Мартин-Лефом (Martin-Lof). Он заключается в разбиении вероятностного пространства последовательностей на неслучайные и случайные (последних относительно много). Неслучайными считаются последовательности, в которых наблюдаются какие-либо закономерности. Последовательность признается случайной, если она проходит набор определенных тестов, предназначенных для выявления закономерностей. Однако если требовать, чтобы последовательность прошла любой статистический тест, то окажется, что СП вообще не существует. На практике используют некоторый набор тестов, где доля СП, им не удовлетворяющих, стремится к 0 при неограниченном увеличении длины последовательностей.
В последние десятилетия в связи с требованиями, возникающими в криптографических приложениях, сформировался криптографический подход к определению СП, где последовательность считается случайной, если вычислительная сложность поиска закономерностей не меньше заданной величины. Этот подход согласован с существующим системным подходом к определению стойкости криптографических систем.
Указанные подходы к определению случайности имеют недостатки. Частотный подход затруднен на практике неопределенностью правил выбора подпоследовательностей, сложностной подход влечет необходимость уменьшения избыточности языка программирования. Использование количественного подхода затруднено определением множества тестов, применяемых к исследуемым последовательностям. Нижние оценки сложности криптографического подхода ориентированы на набор известных тестов, а он со временем может пополняться, что приводит к переоценке сложности. Вместе с тем, для криптографических приложений наиболее подходящим является криптографический подход, учитывающий статистические свойства последовательностей и область их применения.
Тестирование ПСП
Доказано (Herring, C., Palmore, J.I. Random Number Generators are Chaotic, 1995), что любая алгоритмическая реализация последовательности является несовершенной, то есть истинно случайная последовательность не может быть вычислена по какому-то правилу и, следовательно, она должна быть непериодической бесконечной последовательностью. Генерируемые по определенному правилу последовательности, имитирующие РРСП, называются псевдослучайными последовательностями (ПСП). Удачная имитация понимается как близость ряда характеристик генерируемых ПСП к аналогичным характеристикам ИСП.
Порождение ПСП, используемых в криптографических приложениях, основано на реализации многократных итераций определенного преобразования конечного множества Х (часто Х есть множество двоичных n-мерных векторов). Такая выходная последовательность является периодической. Однако длина периода может быть весьма большой, это гарантируется, в частности, использованием линейных регистров сдвига с примитивными характеристическими многочленами. Для многих генераторов ПСП доказаны хорошие статистические свойства и высокая линейная сложность, большая длина периода, однако доказать аналитические и статистические свойства часто не удается. Тогда для обоснования многих свойств используются статистические тесты.
Многообразие критериев оценки ПСП чрезвычайно велико. Каждый из подходов к анализу последовательностей можно отнести к одной из двух групп.
Первая группа связана с поиском закономерностей, позволяющих воспроизвести последовательность по ее отрезку небольшой длины. При этом основные требования к последовательности сводятся к отсутствию в ней относительно простых межзнаковых зависимостей.
Вторая группа критериев связана с оценкой статистических свойств последовательности: имеется ли в исследуемой последовательности какой-либо частотный дисбаланс, позволяющий аналитику прогнозировать по известному отрезку последовательности следующий (предыдущий) знак, то есть предположить значение следующего (предыдущего) бита с вероятностью большей, чем при случайном выборе? Основные требования к ПСП по второй группе критериев сводятся к тому, чтобы ряд ее статистических свойств соответствовал свойствам ИСП, в частности, в ПСП должны быть равномерно распределены частоты встречаемости и отдельных знаков, и s-грамм при достаточно больших значениях s.
При системном подходе для анализа последовательностей используются известные тесты и разрабатываются новые тесты с учётом особенностей анализируемого объекта. Если в ходе анализа в некотором классе последовательностей обнаруживается новая слабость, то разрабатывается соответствующий новый тест, который пополняет используемый набор известных тестов.
Обе группы методов анализа последовательностей составляют системный подход к анализу ПСП, в частности, к разработке поточных шифров.
Одна из первых формулировок основополагающих требований к статистическим свойствам периодических двоичных ПСП была дана С. Голомбом. Эти требования к последовательностям получили известность в криптографии как постулаты Голомба (Golomb S.W. Shift Register Sequences, 1967). Постулаты Голомба приведены, в частности, в монографии [7]. Постулаты исходят из условия сохранения положительных статистических свойств, присущих линейным рекуррентным последовательностям с максимальной длиной периода.
Правила Голомба не гарантируют высокого качества ПСП и являются скорее необходимыми. На практике использование постулатов Голомба для оценки качества ПСП затруднительно, в силу сложности теоретического расчета длин периодов ПСП, частот s–грамм на периоде, а также значений функции автокорреляции. Расчет на ЭВМ возможен лишь для ПСП с небольшой длиной периода, что ограничивает использование постулатов Голомба в криптографических приложениях.
Цель и задачи статистического тестирования ПСП
Тестирование ПСП на случайность – это способ выявления ее определенных свойств с помощью сравнения характеристик ПСП с аналогичными характеристиками ИСП.
С помощью статистического тестирования ПСП решаются следующие задачи:
1) оценка свойств выходной последовательности генератора ПСП с точки зрения использования в криптографическом алгоритме (например, в качестве секретного ключа);
2) оценка качества криптографических примитивов (хэш-функций, блочных и поточных шифров) по их выходным последовательностям, от которых требуется неотличимость от ИСП, в частности, проверка таких криптографических свойств, как лавинный эффект изменения выходных данных алгоритмов при искажениях, корреляция промежуточных и выходных последовательностей;
3) идентификация генераторов ПСП, выдающих «неслучайные» последовательности; разработка новых генераторов ПСП; проверка корректности реализации генераторов ПСП.
Суть тестирования обычно сводится к проверке так называемой «нулевой гипотезы» H0 относительно исследуемой последовательности x(k)=(x_1,…,x_k) длины k, согласно которой x получена на основе k независимых испытаний вероятностной схемы с равномерным распределением.
Вообще статистический тест Т есть двузначная функция
 ,
,где A* – множество последовательностей в алфавите А. Статистический тест Т разделяет множество V(k) последовательностей длины k на множество V(k,0) «неслучайных» последовательностей (как правило, относительно небольшое) и множество V(k,1)=V(k)/V(k,0) случайных последовательностей. Вероятность P того, что тест отвергает случайно выбранную двоичную последовательность x(k), равна V(k,0)/2^k. Как правило, в реальных тестах P не превышает 0,01.
Сложность точного вычисления функции Т велика ввиду громоздкости области определения. Поэтому статистическое тестирование для принятия/отклонения гипотезы H0 выполняется с помощью статистики f_T, то есть относительно просто вычислимой функции, отображающей множество последовательностей во множество действительных чисел, и вероятностного распределения статистики для гипотезы H0, определяемого теоретико-вероятностными методами. Статистический тест – это совокупность статистики, вычисленной по исходным данным, и решающего правила, в соответствии с которым по значению статистики определяют, принять или отклонить гипотезу H0.
Статистический тест является вероятностным, то есть возникают ошибки двух родов, являющиеся важными характеристиками теста:
1) ошибка a первого рода, если последовательность случайна, но H0 отклоняется;
2) ошибка b второго рода, если последовательность не случайна, но H0 принимается.
Решение о прохождении последовательности статистического теста принимается на основе различных критериев [7].
На основе порогового значения. Подход основан на вычислении для данной последовательности x(k) статистики теста f_T(x(k)) и её последующем сравнении с некоторым пороговым значением c(k). В соответствии с критерием двоичная последовательность x(k) не проходит статистический тест, если f_T(x(k))<c(k). Такой подход дает ошибочные решения относительно часто и считается не вполне надежным.
На основе фиксированного доверительного интервала. При данном подходе последовательность x(k) не проходит статистический тест, если f_T(x(k)) находится вне пределов доверительного интервала значений статистики, вычисленного для заданного уровня значимости a. При меньших уровнях значимости ширина доверительного интервала больше. Данный критерий более надежный по сравнению с первым.
На основе вычисления p-value. Третий класс критериев опирается на вычисление характеристики теста из сегмента [0,1], называемой p-значением (p-value). Статистика теста, рассматриваемая как случайная величина с известным законом распределения, строится так, чтобы большие значения указывали на некий дефект случайности последовательности. Значение вероятности p-value есть вероятность того, статистика теста примет значение большее, чем наблюдаемое при опыте в предположении случайности последовательности. То есть малые значения p-value соответствуют неслучайности последовательности. Решающее правило: при уровне значимости a последовательность x(k) не проходит статистический тест, если p-value<a. Значения a следует брать из интервала [10^(-3);10^(-2)]. Преимущество данного подхода по сравнению с прежними в том, что единожды рассчитанную вероятность p-value сравнивают с любым выбранным уровнем значимости без дополнительных расчетов.
Таким образом, основные этапы тестирования ПСП таковы:
1. формулировка гипотезы Н0 случайности последовательности;
2. задание уровня значимости a (вероятности ошибки 1-го рода), обычно a берется из интервала [10^(-3);10^(-2)];
3. вычисление значения статистики f_T(x(k)) для исследуемой последовательности x(k);
4. вычисление p-value из интервала (0;1) по формуле, зависящей от конкретного теста;
5. сравнение p-value со значением a: если p-value >a, то тест пройден.
Существующие инструменты для статистического тестирования ПСП
Для выявления закономерностей к анализируемым ПСП (а также к их отрезкам различной длины) применяется широкий спектр различных статистических тестов. В последние десятилетия разработано большое количество тестов для анализа ПСП. Приведем известные наборы статистических тестов:
1. 11 тестов: Donald Knuth (Stanford University), The Art Of Computer Programming Vol. 2 Seminumerical Algorithms, www-cs-faculty.stanford.edu/~uno/taocp.html
2. 15 тестов: Andrew Rukhin, et. al. (NIST ITL), NIST Statistical Test Suite, csrc.nist.gov/groups/ST/toolkit/rng/documentation_software.html
3. 12 тестов: George Marsaglia (Florida State University), DIEHARD, stat.fsu.edu/pub/diehard
4. 11 тестов: Pierre L’Ecuyer, Richard Simard (Departement d’Informatique et de Recherche Operationnelle Universite de Montreal), TestU01, www.iro.umontreal.ca/~simardr/testu01/tu01.html
5. 5 тестов: Helen Gustafson, et. al.(Queensland University of Technology), Crypt-XS, коммерческая версия, www.qut.edu.au/institute-for-future-environments
Существуют другие описания и реализации статистических тестов, во многом повторяющие тесты из представленных выше наборов:
1. Alfred Menezes и др., Handbook of Applied Cryptography
2. Peter Hellekalek (University of Salzburg), The pLab Project, random.mat.sbg.ac.at
3. John Walker (Autodesk, Inc.), ENT, www.fourmilab.ch/random
4. Robert G. Brown (Duke University), Dieharder, www.phy.duke.edu/~rgb/General/dieharder.php
5. George Marsaglia (Florida State University), Wai Wan Tsang (The University of Hong Kong), «Distilled» version of Diehard, www.jstatsoft.org/v07/i03
Несмотря на немалое количество существующих реализаций статистических тестов ПСП, данное направление постоянно развивается, и в настоящее время активно появляются новые проекты, которые предлагают новые реализации рассмотренных тестов, в том числе, в условиях распределенных вычислительных систем.
Рассмотренные наборы статистических тестов ПСП составляют удобный и гибкий инструмент исследования генераторов ПСП, применяемых в криптографических приложениях.
Пакет NIST STS обладает большей гибкостью, расширяемостью и эффективностью (с точки зрения временных затрат на осуществление тестирования) и является наиболее полным из имеющихся пакетов для статистического тестирования двоичных последовательностей (подробнее можно посмотреть в работах [5], [8], [9]). Тесты пакета NIST STS подробно рассмотрены в статье «Статистические проверки случайных чисел методами NIST» habrahabr.ru/company/securitycode/blog/237695 [3]. На основе пакета NIST STS могут быть построены методики более полного статистического и структурного анализа последовательностей, учитывая то, что для надежной оценки качества ПСП, выработанной генератором, целесообразно проводить не одно, а несколько испытаний.
Все тесты направлены на выявление различных дефектов случайности. Подробнее о выявляемых дефектах случайности можно посмотреть в работе [8].
На практике принятие или отвержение нулевой гипотезы основывают на результатах применения нескольких независимых тестов. Когда независимые тесты приводят к различным выводам, используется комбинирование результатов тестов с помощью статистик, учитывающих совокупность результатов всех использованных тестов. При небольшом количестве комбинируемых тестов используется статистика Фишера-Пирсона, которая сравнивается с распределением хи-квадрат. Если количество комбинируемых тестов велико, то рекомендуется применение теста Колмогорова-Смирнова.
В таблице 1 даны некоторые тесты, рекомендуемые для тестирования ПСП различных длин.
Таблица 1. Статистические тесты для ПСП различных длин
Предварительный анализ рассмотренных статистических тестов позволил определить, какие из них наиболее пригодны для использования в различных задачах разработки средств криптографической защиты информации.
Список использованной литературы
1. Агибалов Г.П. Избранные теоремы начального курса криптографии. Учебное пособие. Томск: Изд-во НТЛ, 2005. – 116 с.
2. Архангельская А.В. Построение высокоскоростных квантовых генераторов случайных чисел для систем защиты информации. Диссертация на соискание ученой степени кандидата технических наук, Москва, 2008. – 182 с.
3. Блог Кода Безопасности: Статистические проверки случайных чисел методами NIST. – habrahabr.ru/company/securitycode/blog/237695
4. Варфоломеев А.А., Жуков А.Е., Пудовкина М.А. Поточные криптосистемы. Основные свойства и методы анализа стойкости. Учебное пособие, М.: ПАИМС, 2000. – 272 с.
5. Вильданов Р.Р., Мещеряков Р.В., Бондарчук С.С. Тесты псевдослучайных последовательностей и реализующее их программное средство // Математическое обоснование и теоретические аспекты информационной безопасности. – www.tusur.ru/filearchive/reports-magazine/2012-25-2/108.pdf
6. Потий А.В., Орлова С.Ю., Гриненко Т.А. Статистическое тестирование генераторов случайных и псевдослучайных чисел с использованием набора статистических тестов NIST STS.
7. Фомичев В.М. Методы дискретной математики в криптологии, М.: Диалог-МИФИ, 2010. – 424с.
8. Rukhin, A., Soto, J., Nechvatal, J., Smid, M., Barker, E., Leigh, S., Levenson, M., Van- gel, M., Banks, D., Heckert, A., Dray, J., Vo, S. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. – www.csrc.nist.gov/publications/nistpubs/800-22/sp-800-22-051501.pdf.
9. Soto Juan, Statistical Testing of Random Number Generators, National Institute of Standards & Technology. – csrc.nist.gov/groups/ST/toolkit/rng/documents/nissc-paper.pdf


hellman
Ай-ай-ай, воровать тележки из супермаркетов нехорошо:
lostpassword
isden
lostpassword
А вы хорошо себя вели в этом году? Говорят, тележки приезжают только к послушным мальчикам и девочкам.
koldyr
предупрежать надо, что X конечно.
с колмогоровской сложностью — не совсем понятно. если взять реализацию как есть — бесконечную, то, я думаю, вообще невозможно построить её (реализации) алгоритмическое описание.
если же взять префикс реализации, то существует язык в котором его описание имеет длину 2.
hellman
Колмогоровская сложность — очень теоретическая штука. Например, она невычислима…
То что вы написали про длину 2 — верно, но нету такого «языка программирования», для которого все строки длины N можно описать программами длины 2. То есть КС есть смысл рассматривать на совокупности строк, а не на одной конкретной.
Ares_ekb
Наверное это наивно, но я думал, что с появлением теорий хаоса, бифуркаций проблема с генерацией случайных последовательностей чисел вообще снимается… Какое-нибудь логистическое преобразование или аттрактор Лоренца разве не позволяют генерить совершенно непредсказуемые последовательности? Интересно было бы их протестировать с помощью методов, описанных в статье.
VolCh
У компьютера (цифрового) конечное число состояний и переход из одного в другое строго детерминирован. Когда-нибудь мы получим такое же состояние как уже было и все следующие будут предсказуемыми, последовательность зациклится, станет периодической, а значит по определению не будет случайной.
Чисто вычислительными методами на цифровом компьютере случайную последовательность точно не получить. Максимум, можно применять вычислительные преобразования к внешним источникам энтропии, но если они реально случайные, то нет смысла и применять преобразования.
Ares_ekb
Да, вы правы, я туплю… Вот, например, логистическое отображение:
При малейших изменениях параметров результат конечно сильно меняется:
lm_rand(0.5, 3.9, 100) = 0.9546
lm_rand(0.49, 3.9, 100) = 0.6160
lm_rand(0.5, 3.9, 101) = 0.1689
lm_rand(0.5, 3.91, 100) = 0.8881
Но если запускать его с теми же самыми параметрами, то результат будет один и тот же.
Насчёт зацикленности и предсказуемости не могу с вами согласиться. При определенных значениях параметра r колебания должны быть совершенно хаотическими, апериодическими. Т.е. получив скажем миллион случайных значений мы вряд ли увидим тут какую-то периодичность и не сможем по не скольким известным значениям предсказать следующие. Нужно знать алгоритм и исходные параметры.
Интересно, сделают ли когда-нибудь компьютеры, основанные на теории хаоса…
VolCh
Мелко плаваете — миллион. Как насчёт 2^64 (грубо — адресное пространство 64-бит процессоров) значений, например?
Ares_ekb
Хотел написать, что вы не правы, что хаос на то и хаос, что там нет никаких периодов. А человеку, который их найдёт дадут Нобелевскую премию. Но, блин, компьютеры, ведь, действительно дискретные. Если длина последовательности сравнима с точностью вычислений, то логистическое отображение однозначно начнёт повторяться. Например, если 64-битная точность вычислений, то на последовательности 2^64 однозначно будут периоды.
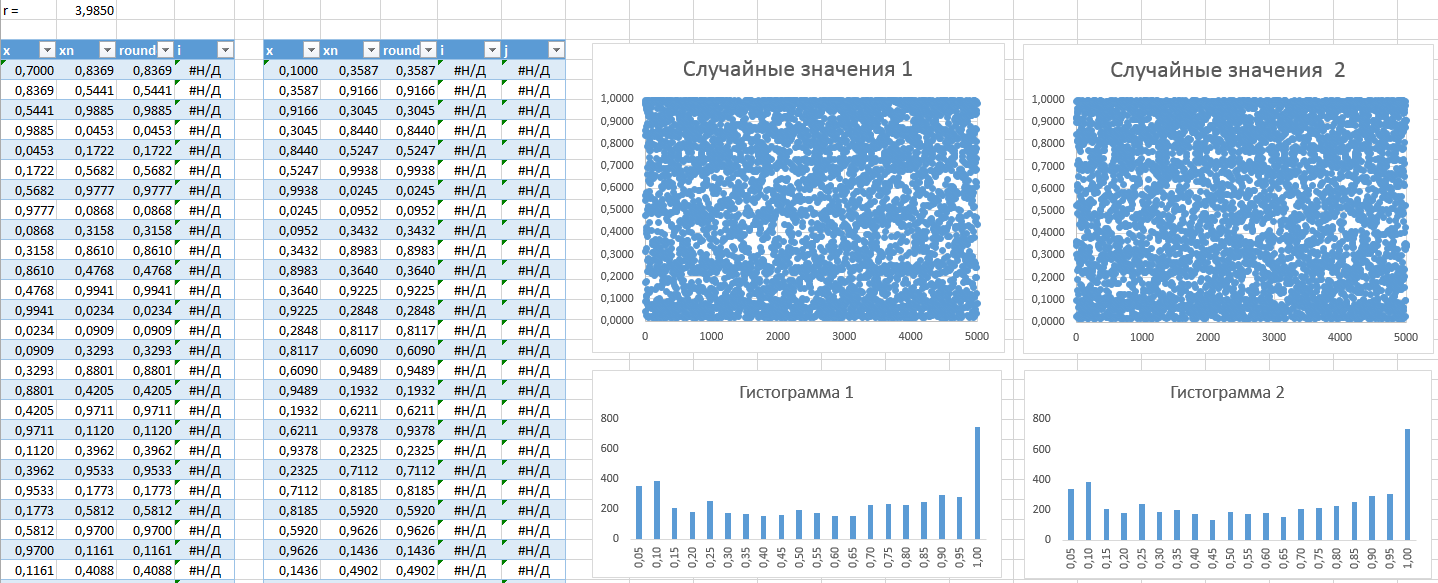
Кому интересно логистическое отображение, для теста нагенерил случайных чисел в Excel. Там две последовательности по 5000 значений. В них период, очевидно, не нашёл. Но на более длинных последовательностях он будет из-за ограниченной точности вычислений.
Хотя, если добавить в вычисления хотя бы текущее время, я думаю периодов можно избежать.
Ares_ekb
Дык, а собственно, в чём проблема? Сделать генератор флуктуаций, ведь, не очень сложно. Почему их не встраивают во все процессоры? Почему бы в арифметику для чисел с плавающей точкой не добавить немного случайности? Чтобы, скажем, последний разряд мог принимать действительно случайные значения.
Это конечно звучит безумно. У программистов всё должно быть абсолютно детерминировано. Но, по-моему, немного хаоса тут не помешало бы.
VolCh
Ну, Интел точно начала встраивать. Другое дело, насколько мы можем доверять Интел в этом вопросе.