В этой статье мне хотелось бы рассказать об одном придуманном когда-то алгоритме (или скорее всего — переизобретённом велосипеде) построения плавного графика по заданным точкам, используя кривые Безье. Статья была написана под влиянием вот этой статьи и очень полезного комментария товарища lany, за что им отдельное спасибо.
Постановка задачи
Есть массив Y-ков точек, расположенных равномерно по оси X. Нужно получить плавный график, который проходит через все заданные точки. Пример на рисунке ниже:
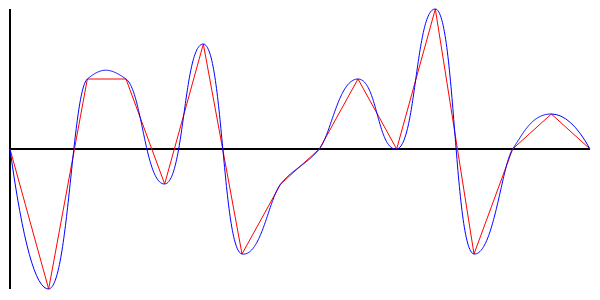
Всех, кому интересно, прошу под кат.
Существует ряд стандартных решений для проведения плавной кривой через точки (по этому поводу много интересного написано в уже упомянутой статье) таких, как например, интерполяции сплайнами. Когда на третьем курсе был придуман этот алгоритм, слово «интерполяция» вселяло в меня ужас, а гугление по запросу «сглаживание графиков» не давало посильных пониманию результатов. Но как-то я дошел до кривых Безье и уж очень они мне понравились. Рисует быстро, алгоритм интуитивно понятный… Что еще надо для счастья. Ну и как-то понеслось.
Основная идея
Разобью идею на три подпункта, чтобы было понятней и читабельней.
- О кривых Безье хорошо написано на вики и на javascript.ru. Если внимательно читать, то можно обратить внимание, что кривая Безье выходит из первой точки касательно к прямой начальная_точка-первая_опорная_точка. Аналогично и в конце — кривая заходит касательно прямой последняя_опорная_точка-конечная_точка. Таким образом получается, что если у нас одна кривая заканчивается в точке А и зашла касательно к прямой а, а другая кривая выходит из этой точки А касательно к той-же прямой а, то этот переход между двумя кривыми Безье у нас получится плавным.
- Исходя из первого пункта получается, что у нас опорные точки слева и справа относительно точки А должны лежать на одной прямой. Поразмыслив немного, было решено, что эта прямая должна быть такой, чтобы ?BAB1=?CAC1 (рисунок ниже), где точки B1 и C1 — опорные.

- Расстояние от точки А до точек B1 и C1 было решено взять равным половине шага по X между точками B и A, A и C, и т.д. Мне сложно как-то обосновать такой выбор, но важно, чтобы это расстояние было меньше, чем шаг по X между точками А и B, иначе может получится что-то такое, как на рисунке ниже. Важно понимать, что чем больше будет это расстояние, тем более извилистой будет кривая и наоборот. Расстояние в половину шага по X мне кажется оптимальным, но тут уже возможны варианты.

Таким образом получается, что задача сводится к поиску прямой (B1C1) и, собственно, опорных точек B1 и C1, по которым мы потом будем строить кривые Безье.
Поиск прямой
Как известно, прямая на плоскости выражается формулой y=kx+b, где k — тангенс угла наклона прямой к оси Х, а b — «высота» пересечения прямой и оси Y.
Поиск коэффициента k
Скажу наперед, что k = tg(?) = tg((?-?)/2) = (Sqrt(((YA-YB)2+?X2)*((YA-YC)2+?X2))-?X2-(YA-YB)*(YA-YC)) / (?X*(YC-YB)), где ?X — расстояние по Х между точками графика (напомню, что у нас точки расположены равномерно по Х). Ниже представлено математическое доказательство правильности формулы, но если вы не в настроении, то можете его просто пропустить.

- Пускай угол ?O1BA=?, а угол ?O2СA=?.
Тогда ?BAO1=90o-?; ?CAO2=90o-?, так как ?ABO1 и ?ACO2 — прямоугольные.
- (1) ?B1AС1=?B1AB+?BAO1+?O1AС+?CAС1=180o
(2) ?B1AB=?C1AС — по условию
(3) ?BAO1=90o-?
(4) ?O1AС=?CAO2=90o-?
Из (1), (2), (3) и (4) получается, что:
2*?C1AС+(90o-?)+(90o-?)=180o
2*?C1AС+180o-?-?=180o
(5) ?C1AС=(?+?)/2
- (6) ?C1AС=?C1AD+?DAC=?+?DAC
(7) ?DAC=?O2CA=? — как внутренние разносторонние углы образованные двумя параллельными прямыми (AD) и (O2C) и секущей (AC)
Из (5), (6) и (7) получается, что:
?C1AС=?+?DAC
(?+?)/2=?+?
?+?=(?+?)/2
(8) ?=(?-?)/2
- k=tg(?)=tg((?-?)/2)
Из ?ABO1:
sin(?)=[AO1]/[AB]
cos(?)=[BO1]/[AB]
Из ?ACO2:
sin(?)=[AO2]/[AC]
cos(?)=[CO2]/[AC]
Под квадратными скобками подразумевается длинна отрезка (не хотел использовать вертикальные прямые — надеюсь, что читатель меня простит)
- Из предыдущего подпункта следует:

- Зная, что:
[BO1]=[CO2]=?X
[AO1]=YA-YB
[AO2]=YA-YC
[AB]=Sqrt([AO1]2+[BO1]2)=Sqrt((YA-YB)2+?X2)
[AC]=Sqrt([AO2]2+[CO2]2)=Sqrt((YA-YC)2+?X2)
Получаем, что:

И так, k мы нашли. Забегая наперед скажу, что b нам при расчетах не пригодится. Приступим к поиску опорных точек.
Ищем опорные точки
Сразу скажу, что:


Из ?AC1O:
?X'=[AO]=[AC1]*cos(?).
[C1O]=[AO]*tg(?)=k*?X'
Если мы принимаем [AC1] равным половине шага по X между основным точками графика (точками B и A, A и C, т.д.), то:

И вот, собственно:
XC1=XA+?X'
XB1=XA-?X'
YC1=YA+k*?X'
YB1=YA-k*?X'
К приятному!
- От товарища lany (огромное ему за это спасибо и плюс ему к карме) я узнал, что html5 с помощью функций quadraticCurveTo() и bezierCurveTo() умеет рисовать по canvas-у кривые Безье сам. Соответственно, алгоритм можно применить с JavaScript-ом.
- Приятной особенностью алгоритма есть то, что график предсказуемо «выпирает» за границы пространства точек, через которые мы собственно проводим график. Если брать расстояние до опорных точек равными половине шага по X (отрезок [AC1] на последнем рисунке), то зазора в четверть шага по X сверху и снизу от границ canvas-а будет достаточно.
Пример реализации на JSFiddle
UPDATE:
- Попытки сделать так, чтобы опорные точки нужно было считать один раз, а потом, при масштабировании графика, просто использовать их координаты, потерпели неудачу. Все упирается в то, что в расчет коэффициента k входит и текущий масштаб по X, и текущий масштаб по Y. И вытянуть их из формулы не выходит. Товарищ quverty меня об этом предупреждал и оказался прав.
- Хотел бы еще раз обратить внимание, что кривизну построенного графика можно регулировать. Для этого следует изменять расстояние до опорных точек — менять коэффициент
?X'=?X/2*Sqrt(1/(1+k2)) , а именно — знаменатель вот этого его кусочка:?X/2 . Знаменатель меньше 1 брать не следует (читай третий подпункт пункта «Основная идея»). Поэкспериментировать можно на JSFiddle (129 строка JavaScript-а). - Обратите внимание на реализацию сплайна Катмулла-Рома товарища IIvana. И спасибо ему за этот комментарий.
Комментарии (53)

deniskreshikhin
03.05.2016 13:58-1Кстати, с помощью кривых Безье легко получит простейшую аппроксимацию без «математики»:
function drawByCurves(ctx, points){ ctx.beginPath(); ctx.moveTo(points[0].x, points[0].y); for(var i = 1; i < points.length - 2; i ++){ var xc = (points[i].x + points[i+1].x) / 2; var yc = (points[i].y + points[i+1].y) / 2; ctx.quadraticCurveTo(points[i].x, points[i].y, xc, yc); } ctx.quadraticCurveTo(points[i].x, points[i].y, points[i+1].x,points[i+1].y); ctx.stroke(); }
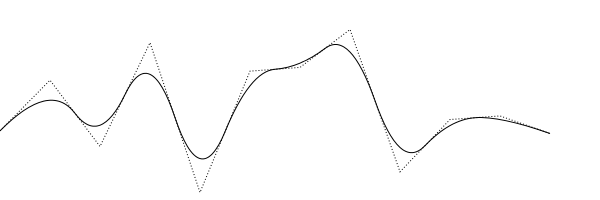
https://jsfiddle.net/DenisKreshikhin/1oLyt2jz/
StreetAngel
03.05.2016 14:24+3https://jsfiddle.net/1oLyt2jz/4/
И более «плавнее», у автора кривая описанная а тут вписанная получается
deniskreshikhin
03.05.2016 14:31+1Ну это разного рода алгоритмы, у автора интерполяция, т.е. когда кривая проходит через все заданные точки.
А аппроксимация это когда кривая более-менее похожа на оригинал, но не обязательно проходит через все точки. Может вообще общих точек не иметь.

HOMPAIN
03.05.2016 17:01У вас ошибка в первой строчки математики. Должно быть => cos(f)= +- sqrt(..) (забыл минус)

Nabytovych
03.05.2016 17:03Корректное замечание. Но там дальше используется и +?X', и -?X', поэтому этот недочёт нивелируется

Nabytovych
03.05.2016 17:08Там ?X' идет как длинна стороны треугольника (AC1O), а длинна стороны не может быть отрицательной. Поэтому знак не учитывался. Но замечание корректное и за него спасибо

quverty
03.05.2016 17:07Я когда-то такую идею с равными углами встроил в свой векторный редактор… и через некоторое время осознал, что если картинка масштабируется по разному по Y и по X, то кривая вместо такого-же изменения масштаба должна поменять форму, если хочется чтобы углы между касательными остались одинаковыми. Но так как других идей так и не придумал, то всё оставил как было. Не знаю, можно ли тут что-то другое предложить.

Nabytovych
03.05.2016 17:15Не уверен, но по идее, если сохранять координаты опорных точек (а это львиная доля вычислений в алгоритме), и потом масштабировать и координаты точек графика, и координаты опорных точек, и по ним заново проводить кривые Безье, то все должно работать. Нужно попробовать как-то.
Кривая поменяет форму, но выйдет ли использовать уже посчитаные координаты опорных точек… Было бы здорово.
quverty
03.05.2016 17:23Я тогда решил, что форма не должна меняться, так что после расчёта при заданном масштабе всё приводилось в такой вид, чтобы после изменения масштаба форма не менялась, хотя углы уже переставали быть равными. Для меня так было удобнее, тем более что я там ещё какой-то метод построения кривых Безье использовал. Давно это было, в те времена когда inkscape был мне не доступен и приходилось выкручиваться чтобы в статью картинку вставить не нарушая никаких лицензий.
IIvana
03.05.2016 18:28Когда на третьем курсе был придуман этот алгоритм, слово «интерполяция» вселяло в меня ужас, а гугление по запросу «сглаживание графиков» не давало посильных пониманию результатов. Но как-то я дошел до кривых Безье и уж очень они мне понравились. Рисует быстро, алгоритм интуитивно понятный… Что еще надо для счастья.
Собственные алгоритмы всегда интуитивно понятнее ). Но рискну предположить, что обычный Катмулл-Ром на порядок проще и понятнее. Найти можно много где, в т.ч. и здесь https://habrahabr.ru/post/282441/

SEOVirus
03.05.2016 20:18А где это применимо? :)

Nabytovych
03.05.2016 20:32Надеюсь, что кому-то в вебе пригодится) Мне когда-то в курсаче на третьем курсе универа пригодилось))

Nabytovych
03.05.2016 20:28Я долго и безрезультатно пытался сделать в коде на JSFiddle так, чтобы можно было один раз запомнить опорные точки, а потом, при масштабировании расстянуть координаты точек графика и координаты опорных точек, и заново провести кривые Безье, не пересчитывая собственно координаты опорных точек. Если у кого-то есть какие-то идеи по этому поводу (а еще лучше — реализации), то я буду очень благодарен. Или если кто-то уверен, что этого сделать не выйдет — тоже напишите. А то товарищ quverty на такую идею классную с масштабированием натолкнул…
Там есть три строчки закомментированные (№№137, 151, 152). Если их раскомментировать, то на canvas-е нарисует еще и опорные точки
quverty
03.05.2016 21:06Мне кажется, что уже просто то, что при масштабировании по вертикали какие-то углы перестают быть равными и надо все перестраивать, говорит что для построения графика это не особо подходит. График не должен как-то дополнительно изменяться помимо самого масштабирования. А вот на рисунках это не выглядит проблемой. А то порой приходится все эти узлы каждый раз двигать у каждого стыка когда рисуешь с использованием кривых Безье.

Nabytovych
03.05.2016 21:20У меня просто чувство такое, что хоть углы и меняются, но построенные кривые Безье должны просто расстянутся. Там даже если просто в JSFiddle порастягивать график, то видно (если показать еще и опорные точки), что кривые просто расстягиваются, не меняя как-то кривизну или свои изгибы. И мне это не дает покоя. Было бы круто, если бы в веб-е получилось в риал-тайме масштабировать график)
Но руки что-то не позволяют реализовать это. То ли я туплю, то ли алгоритм таки не позволяет стягивать-расстягивать canvas без перерассчета опорных точек…
quverty
03.05.2016 21:21Нет, я уже на эти грабли наступал.

Nabytovych
03.05.2016 21:24А было бы классно, если можно было не пересчитывать)
Но если нет — то нет. Поверю на слово
quverty
03.05.2016 21:28Там видимо не углы надо равными делать, а что-то другое, тогда и точки не надо пересчитывать. А на вашем конкретном графике вроде вообще не особо заметно что углы меняются и кажется что всё почти О'К

Nabytovych
03.05.2016 21:37Не совсем то. Через углы я вышел на опорные точки. Посчитал их. Все, дальше за углы я забываю и иду от координат опорных точек. Координаты ОТ (опорных точек, дальше буду сокращать) я сохранил в массиве. Когда идет масштабирование, я пропорционально пытался растянуть и координаты точек графика, и координаты ОТ. И тут у меня что-то не получается… И я вот не знаю где беда — у меня в кривизне рук, или в том, что алгоритм не позволяет. По идее — все должно работать. А на практике… И я вот теряюсь в догадках. С одной стороны — там в рассчетах координат ОТ идут квадраты и корни от координат точек графика. А с другой — по ощущениях, все должно получатся при масштабировании.

Nabytovych
03.05.2016 21:40Как-то вот так…

quverty
03.05.2016 21:46А когда график начинаешь растягивать углы перестают быть равными, если они расположены не симметрично. Вроде бы так, если я что-то не упустил.

Nabytovych
03.05.2016 21:53У меня просто бред получался. Я брал по умолчанию шаг по X равен 1, а по Y — то, что в исходных данных. Потом считал опорные точки и сохранял их в массив. А потом, когда отрисовывал, все масштабировал. И у меня получался бред. И я не знаю, то ли я втупил, то ли… нельзя так масштабировать. Было бы классно, если бы кто-то обосновать смог это все.

quverty
03.05.2016 21:58Есть идея провести один отрезок вертикально из В1 на АВ, а другой из С1 на АС и требовать равенства этих отрезков а не углов, и может тогда всё будет масштабироваться правильно.

Nabytovych
03.05.2016 22:07Не то. Эти отрезки изначально не равны (если идти от равенства ?BAB1=?CAC1). Можно попробовать сохранять сдвиг опорных точек по X и по Y относительно точки A… И масштабировать его… Надо попробовать

quverty
03.05.2016 22:12Так и надо сделать их равными, тогда при масштабировании они останутся равными. А углы при вертикальном масштабировании перестают быть равными. Это правильно для графика. Я использовал равенство углов в редакторе, так как там более важно было то, что картинка правильно ведёт себя при вращении, хотя при этом получалась проблема при разном изменении масштаба по каждой оси.

Nabytovych
03.05.2016 22:22Надо посоображать про это все. И попробовать в коде.
Я наверное до завтра break сделаю. А на завтра попробую что-то родить. Интересно с этим всем получается)
quverty
03.05.2016 22:24Просто был какой-то древний редактор (DrHalo) который со всем этим замечательно справлялся, но я что-то так и не понял как, несмотря на многочисленные эксперименты.

iga2iga
03.05.2016 21:57Понятно, конечно, что кривые проходят именно через точки, но будь по оси Y температура а по X время (рис.1), и до вершины второй кривой градусов 100, я бы запаниковал…
IIvana
04.05.2016 01:02+3function drawByCurves(ctx, points) { ctx.beginPath(); ctx.setLineDash([]); ctx.moveTo(points[0].x, points[0].y); var dl = 0; for (var i = 0; i < points.length - 2; i++) { var dr = (points[i+2].y - points[i].y) / 2; var a3 = dl + dr + 2 * (points[i].y - points[i+1].y); var a2 = points[i+1].y - a3 - dl - points[i].y; for (var t = 0; t <= 1; t+=.05) { var y = a3; y = y*t+a2; y = y*t+dl; y = y*t+points[i].y; ctx.lineTo(points[i].x + t * 50, y); } dl = dr; } ctx.strokeStyle = 'blue'; ctx.stroke(); }

Без Безье
Nabytovych
04.05.2016 01:28Ваш зверь пошустрее будет)
P.S.: Разве что выиграю за счет того, что у меня промежуточные точки встроенная функция отрисовывает, а у Вас — цикл с lineTo()IIvana
04.05.2016 01:33Ну вы же понимаете, что это зависит от скорости подкапотной реализации вашей встроенной quadraticCurveTo. И в явном цикле можно тривиально менять шаг.

Nabytovych
04.05.2016 01:36Конечно.
Ваша реализация — это сплайн Катмулла-Рома?IIvana
04.05.2016 01:41Именно. В моей статье на хабре (ссылка выше) есть одна маленькая опечатка в формуле его расчета, в коде выше она исправлена. А вообще формулы выводятся на порядок проще, чем ваши расчеты в статье. Для любого локального сплайна. Которые, кстати, совершенно не освещены в статье на которую вы ссылаетесь (кроме Акимы), да и вообще в той статье сравнивается несравнимое — локальные сплайны с глобальными и т.п.

Nabytovych
04.05.2016 01:51Так у меня же через геометрию все...)
Я про сплайны Акимы до той статьи и не слышал

Nabytovych
04.05.2016 01:53Сплайн Катмулла-Рома, кстати, очень похоже отрисовывает
IIvana
04.05.2016 01:56Потому что они оба — реализации кубического сплайна Эрмита, различие только в алгоримте расчета производных в узлах. Вообще, я наверное не умею писать статьи, если из моей это непонятно :) И как рассчитывать коэффициенты сплайна тоже.

quverty
04.05.2016 20:35В каком смысле оба? Кривая Безье это более общий случай чем кубический сплайн. Я прикинул коэффициенты, получилось что для того, чтобы она выродилась в обычный кубический сплайн надо опорные точки разнести по x на треть расстояния. Уже после этого подбирать коэффициенты по Эрмиту или как нибудь ещё. В примере же половина.
IIvana
04.05.2016 22:21В смысле оба — Катмулл-Ром с Хироши Акимой. А Безье — это именно кривая, а не функция (как сплайн). Если отойти от геометрического алгоритма построения Кастельжо, то насколько я помню, она выражается через параметрические полиномы Бернштейна. Но в любом случае не могу согласиться, что она является более общим случаем сплайна.
ЗЫ если в джаваскрипте есть cubicCurve, то тривиально строится аналогичный алгоритм, как у ТС.
quverty
04.05.2016 22:36Кривая Безье описывается как (x(t),y(t)), где x(t) и y(t) полиномы третьего порядка. Сплайн можно описать той же формулой, если взять x = at+b. Поэтому, если у кривой Безье занулить коэффициенты при кубическом и квадратичном члене для х, то она ничем не отличается от кубического сплайна. Как я уже написал наверху, в том примере с постоянным шагом, который предложил автор поста, для этого достаточно сделать расстояние между опорными точками равным одной третьей шага. Надеюсь не переврал в расчётах.
IIvana
04.05.2016 22:59Навскидку выглядит правдоподобно, соглашусь насчет частного случая при линейной зависимости аргумента от параметра. Честно сказать, в метод предложенный в статье не вчитывался — чукча не читатель, чукча писатель, своих вариантов вагон — девать некуда )

quverty
04.05.2016 23:03Зато если функции нужной не найдётся можно Безье вместо сплайнов использовать.
IIvana
04.05.2016 22:54function drawByCurves(ctx, points) { ctx.beginPath(); ctx.setLineDash([]); ctx.moveTo(points[0].x, points[0].y); var dl = 0, k = 0.33; for (var i = 0; i < points.length - 2; i++) { var dr = (points[i+2].y - points[i].y) / 2 * k; ctx.bezierCurveTo( points[i].x+k*30, points[i].y+dl, points[i+1].x-k*30, points[i+1].y-dr, points[i+1].x, points[i+1].y); dl = dr; } ctx.strokeStyle = 'blue'; ctx.stroke(); }


Рулим коэффициентом k.
ЗЫ так можно и до NURBS с Кочанеками-Бартельсами дойти. Раз уж пошла такая… интерполяция )
quverty
04.05.2016 22:57Что-то страшное действительно. Вообще я имею в виду первая опорная точка 1/3 и вторая 2/3 — ну как тут могут получиться такие страсти?
IIvana
04.05.2016 23:02Все правильно, по 1/3 — см. первую картинку (там и в коде k=0.33 — это именно оно). А вторая картинка при k=1.9, для демонстрации красоты ) И чтобы показать, что этот коэффициент аналогичен коэффициенту натяжения в TCB-сплайне.


EndUser
Не могу разглядеть — где гарантия, что производная f(x) на таком графика меньше бесконечности (и f(x) однозначна)? То есть, что кривая по ходу слева направо в каком либо месте не загнётся справа налево.
Не смог увидеть обоснование зачем эстетическое закругление Безье, которое не проходит через заданные точки, использовать вместо строго интерполяционных полиномов, предназначенных для этого.
Nabytovych
Дайте мне точки, при которых кривая загнется, и я удалю статью.
Читайте пункт «К приятному!».
EndUser
«Ты не романтик!» /Робот Вертер/
Корректность метода всегда на совести предлагающего метод.
DeepBlue
На вики можно найти анимацию с построением кривой Безье. Если опорные точки в ней будут расположены по возрастанию x-координаты, то все промежуточные точки, в т.ч. и последняя, рисующая сам график, будут всегда двигаться слева направо.
При данном выборе опорных точек разница в x-координате между B1 и A не больше половины таковой между B и A (поскольку расстояние между A и B1 равно половине, а длина его проекции на ось x, значит, не больше). Для опорной точки, лежащей справа от B, (назовём её A1) выполнено то же самое. Значит, B, A1, B1, A лежат по возрастанию x, а это нам и требуется.
Есть, правда, один плохой случай, когда A1 и B1 лежат на одной вертикальной прямой, а отрезки BA1 и B1A горизонтальны, но он рассматривается отдельно: на анимации кривой Безье все точки всё равно будут двигаться вправо, кроме той, что движется по отрезку A1B1.
Nabytovych
Не уверен, что правильно понял плохой случай, но алгоритм не должен поставить опорные точки на вертикальную прямую, если соседние слева и справа точки графика лежат на одной горизонтальной прямой с текущей точкой
DeepBlue
Возможно, я неправильно понял алгоритм, но кажется, если синие точки ниже — это график, то две красных станут опорными.

Nabytovych
Все правильно. Но ничего плохого не произойдет, если не брать растояние до опорных точек большим. Собственно, как Вы и говорили