А уж тот, кто плотно работал с графикой, знает эти цифры буквально наизусть — как в былые времена эникейщики запоминали серийники Windows. Иногда коэффициенты округляют до второго знака, иногда уточняют до четвертого, но каноническая форма именно такая.
Вычисляет она относительную яркость цвета (relative luminance или в некоторых контекстах luma; не путать с lightness и brightness) и широко применяется для преобразования цветного RGB-изображения в Grayscale и связанных с этим задач.
Формула растиражирована и процитирована в тысячах статей, форумных обсуждений и ответов на StackOverflow… Но дело в том, что единственно-правильное её место — на свалке истории. Использовать её нельзя. Однако же используют.
Но почему нельзя? И откуда же взялись именно такие коэффициенты?
Мини-экскурс в историю
Есть такая международная организация, которая разрабатывает рекомендации (де-факто стандарты) для сферы телерадиокоммуникаций — ITU.
Интересующие нас параметры прописаны в рекомендациях ITU-R BT.601, принятых в 1982 году (по ссылке обновленная редакция). Уже на этом моменте можно слегка удивиться — где мы и где 82-ой год? Но это только начало.
Циферки перекочевали туда из рекомендаций ITU-R BT.470 от 1970 года (по ссылке также обновленная редакция).
А они, в свою очередь — наследие цветовой модели YIQ, которая была разработана для североамериканской системы телевещания NTSC в 1953 году! К нынешним компьютерам и гаджетам она имеет отношение чуть более, чем никакое.
Никому не напоминает байку про связь космических кораблей с шириной древнеримской лошадиной задницы?
Современные колориметрические параметеры начали выкристаллизовываться в 1970 году с модернизацией систем PAL/SECAM. Примерно в это же время американцы придумали свою спецификацию SMPTE-C на аналогичные люминофоры, но NTSC перешла на них только в 1987 году. Я не знаю наверняка, но подозреваю, что именно этой задержкой объясняется сам факт рождения пресловутых Rec.601 — ведь по большому счету, они морально устарели уже к моменту своего появления.
Потом в 1990 году случились новые рекомендации ITU-R BT.709, а в 1996 на их основе придумали стандарт sRGB, который захватил мир и царствует (в потребительском секторе) по сей день. Альтернативы ему существуют, но все они востребованы в узкоспецифичных областях. И прошло уже, ни много ни мало, 20 лет — не пора бы уже избавиться от атавизмов окончательно?
Так в чем же конкретно проблема?
Кто-то может подумать, что те коэффициенты отражают некие фундаментальные свойства человеческого зрения и потому не имеют срока давности. Это не совсем верно — помимо всего прочего, коэффициенты привязаны к технологии воспроизведения цвета.
Любое RGB-пространство (а YIQ это преобразование над моделью RGB) определяется тремя базовыми параметрами:
1. Хроматическими координатами трех основных цветов (они называются primaries);
2. Хроматическими координатами белой точки (white point или reference white);
3. Гамма-коррекцией.
Хроматические координаты принято задавать в системе CIE xyY. Регистр букв в данном случае важен: cтрочные xy соответствуют координатам на хроматической диаграмме (всем известная «подкова»), а заглавный Y — это яркость из вектора CIE XYZ.
Теперь посмотрим на компоненту Y у всех первичных цветов NTSC (я пометил их розовым):

* Оригинал таблицы со многими другими пространствами на сайте Брюса Линдблума.
Знакомая цифирь, правда? Вот и ответ на вопрос «откуда взялось?»
А проблема в том, что используемое сегодня пространство sRGB существенно отличается от системы 60-летней давности. И дело даже не в том, что из них лучше или хуже — они просто разные:
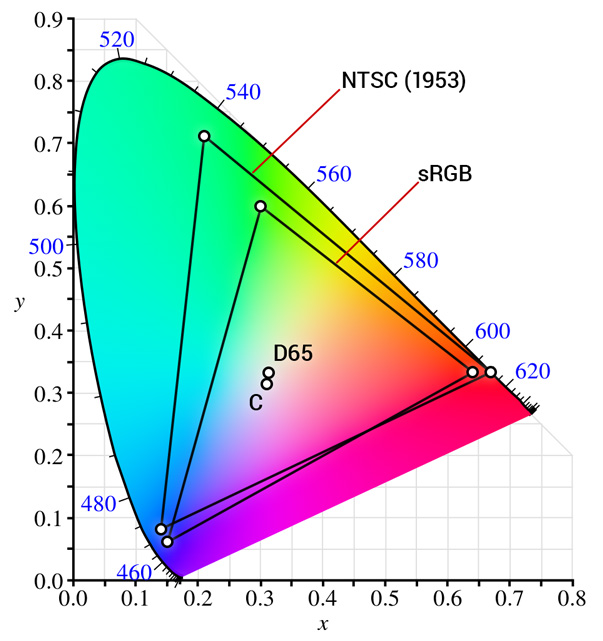
Треугольник шире и смещён в сторону. Другая белая точка. К слову сказать, иллюминант C уже очень давно признан deprecated в пользу иллюминантов серии D вообще и наиболее популярного D65 в частности. Тело цветового охвата другое — соответственно, результаты вычислений яркости окажутся неадекватны реальности.
Вы можете спросить: а зачем древнему NTSC охват (практически совпадает с охватом Adobe RGB 1998!) настолько больше, чем у современного sRGB? Я не знаю. Совершенно очевидно, что кинескопы того времени покрыть его не могли. Быть может, хотели сделать задел на будущее?
Как правильно?
Относительные яркости первичных цветов в пространстве sRGB приведены в таблице выше (помечены зеленым) — их и нужно использовать. На практике обычно делают округление до 4-х знаков:
Внимательный читатель заметит, что коэффициент при R округлен не по правилам (в меньшую сторону), но это не ошибка. Дело в том, что сумма всех трех чисел должна равняться единице, и «правильное» округление внесло бы погрешность. Педанты могут взять все шесть знаков после запятой и не беспокоиться.
Этой формулы хватит для 99% типичных случаев. Её использует во всех своих спецификациях W3C (например, матричные фильтры в SVG).
Если вам нужна бОльшая точность, придется вычислять L*, но это отдельная большая тема. Неплохой ответ на StackOverflow, который дает отправные точки для дальнейшего чтения.
Если изображение у вас в другом цветовом пространстве (Adobe RGB, ProPhoto RGB и т.д.) — коэффициенты будут свои; их можно найти в вышеупомянутой таблице Брюса Линдблума.
Почему меня это волнует?
Как уже было сказано выше, за многие годы формула растиражирована на несметном количестве сайтов, и они сидят в топе всех поисковиков (например). Источники посерьезнее часто приводят обе формулы, но не делают между ними должного различия, преподнося их как равноправные альтернативы. Характерный пример на StackОverflow: Formula to determine brightness of RGB color — ответы довольно подробные, но человеку не в теме сложно сделать осознанный выбор.
Справедливости ради, серьезные проекты такими ошибками почти не страдают — авторы не брезгуют сверяться со стандартами, да и фидбек аудитории работает (хотя и там не обходится без исключений). А вот рядовой программист, которому нужно побыстрее решить задачу, вбивает в поисковик что-то типа «rgb to grayscale», и тот подсовывает ему сами знаете что. Формулу продолжают находить и копипастить до сих пор! Феноменальная живучесть.
На розыск этих примеров я потратил около 20 минут:
- документация Microsoft
- документация Matlab
- стандартная библиотека Go
- модные колор-пикеры для React-а (>2k звезд)
- Chart.js (>23k звезд!)
- библиотека CImg для обработки изображений
- какие-то модули в OpenCV (похоже, что второстепенные)
- коллекция демок на WebGL
- что-то внутри Gimp-а и утилитка к Inkscape
- чьи-то небольшие проекты на Swift, Go, Three.js, JS
Обратите внимание, что наряду со старенькими проектами в списке немало упоминаний самых свежих и модных технологий, то есть код писался/копипастился совсем недавно.
А поводом для написания этой заметки стал слайд из доклада Василики Климовой с HolyJS-2016 — с той же самой доисторической формулой. Понятно, что формула не повлияла на основной смысл выступления, но наглядно продемонстрировала ваши шансы ненароком её нагуглить в 2016 году.
Подытоживая: если увидите в чьем-то действующем коде последовательность 299/587/114 — кидайте автору ссылку на эту заметку.
update 1
В комментариях настоятельно просят примеры. Но тут не всё так просто, как кажется.
Если взять произвольную картинку и перевести её в ч/б двумя способами — это не даст вообще ничего. Картинки будут просто немного разными. Зритель сможет только оценить, какой вариант ему субъективно симпатичнее. А дело-то не в этом! Дело в том, какой вариант правильнее, точнее.
Немного поразмыслив, я набросал вот такую штуку: codepen.io/dom1n1k/pen/LZWjbj
Скрипт генерирует 2 раза по 100 случайных цветов, подбирая компоненты так, чтобы яркость всех кубиков была теоретически одинакова (Y = 0.5). То есть всё поле целиком должно субъективно восприниматься как можно более однородно (однородно именно с точки зрения яркости, не учитывая разные тона).
Слева старая «неправильная» формула, справа новая «правильная». Справа однородность действительно заметно выше. Хотя и не идеальна, конечно — для бОльшей точности нужно вычислять перцептивную светлоту L*.
update 2.1
Ещё возник вопрос по поводу гаммы. Его подняло уже минимум 3 человека, поэтому тоже вынесу в апдейт. Вопрос на самом деле непростой и отчасти даже философский (вполне потянет на отдельную статью).
Если говорить строго — да, для перевода картинки в ч/б вид гамму нужно декодировать. Но на практике (в задачах, не связанных с точной колориметрией) этот шаг часто опускают ради простоты и производительности. Например, Photoshop при конвертации в grayscale гамму учитывает, а одноименный CSS-фильтр (MDN) — нет.
С точки зрения корректности результата, выбор весовых коэффициентов и пересчёт гаммы — взаимодополняющие вещи. Влияет и то, и другое. Разница только в том, что гамма требует дополнительных вычислений, а вот правильные коэффициенты обходятся бесплатно.
Вторая версия демо с учетом гаммы (первая никуда не делась): codepen.io/dom1n1k/pen/PzpEQX
Получилось, конечно, точнее.
Комментарии (118)
VioletGiraffe
28.06.2016 15:13А в контексте YUV исходные коэффициенты валидны, или тоже нет?

dom1n1k
28.06.2016 15:40YUV — это просто преобразование системы координат над RGB-пространством (точнее семейство из нескольких родственных преобразований).
В какой пропорции смешивать — зависит от конкретного RGB-пространства, а оно в свою очередь зависит от контекста задачи.
Если вы вдруг действительно работаете с NTSC-видеосигналом — исходная формула верна. Но только для него. Для других пространств — нет.

Cthutq66a
28.06.2016 15:17А если ч/б картинка используется только для вычислений(например детектор границ) есть разница как ее считать по RGB?

alexkunin
28.06.2016 15:19Контрасты будут другие. Навскидку, новая модель «приглушает» красный и синий каналы, а зеленый наоборот «усиливает».

Cthutq66a
28.06.2016 15:23Это более — менее очевидно. Вопрос скорее — как правильно?

dom1n1k
28.06.2016 15:29+2Правильно — использовать те формулы, которые выведены конкретно для вашего рабочего цветового пространства.
Если это sRGB (подавляющее большинство случаев), то верна формула, которую я привёл (вторая). Если вдруг вы используете что-то иное (Adobe RGB, ProPhoto RGB и так далее) — там будут свои коэффициенты, их можно вывести из таблички Линдблума.

alexkunin
28.06.2016 16:00Правильные коэффициенты зависят от контекста, мне кажется. Если у вас синие буквы (диапазон 0-255) на черном фоне, то умножение на 0.07 оставляет вам диапазон 0-18, примерно 4 бита (а было-то 8!). Я бы постарался не терять столько информации.

evtomax
30.06.2016 12:38И вообще лучше вычислить границы для каждого канала, а потом сделать объединение, иначе потеряются границы между близкими по яркости цветами.
DistortNeo
30.06.2016 20:11Конкретно для вычисления границ можно использовать цветовой градиент Di Zenzo,

sasha1024
30.06.2016 15:59+1По хорошему, наверное (я не специалист), следовало бы не переводить вообще в grayscale в данном случае, а делать вычисления на основе формул цветового отличия. Ну это в идеале. Не знаю, как делают на практике.

RouR
28.06.2016 16:20Выше есть ссылка на фиддл с Леной — смотрите на область вокруг носа, полутени лучше видно

darkAlert
28.06.2016 17:52Разница есть, но единственного «правильного» способа нет.
Изменения формулы rgb_to_gray аналогичны изменению контраста изображения.
Но это палка о двух концах — увеличим контраст, усилим границы, но получим больше шума. И обратно.
Проблема в том, что rgb_to_gray преобразование и последующий оператор Собеля это все линейные преобразования. Изменяя коэффициент в формуле rgb_to_gray мы лишь получаем масштабирование, т.е: Sobel(Rgb2Gray(I*A)) = Sobel(Rgb2Gray(I))*B
Более продвинутым способом можно считать нелинейные преобразования, например те же нейронные сети, обученные на выделение границ.

homm
28.06.2016 15:57если увидите в чьем-то действующем коде последовательность 299/587/114 — кидайте автору ссылку на эту заметку.
Основная проблема в том, что эта заметка на русском. Куда лучше всего всего давать ссылку англоязычным разработчикам (хочу попроваить формулу в Pillow)?

RolexStrider
28.06.2016 16:14+2коэффициенты привязаны к технологии воспроизведения цвета
Именно так и было, но наоборот: привязка изначально была к Ч/Б телевизорам и их особенностям. В целях обратной совместимости. Ну а после… Эти костыли кочуют из руководства в руководство прям аки мировые константы.

Randl
28.06.2016 16:33А разве коэффициенты не зависят от того, в каком цветовом пространстве у нас картинка? Конечно, sRGB сейчас стандарт де-факто, но ведь теоретически изображение может быть и в AdobeRGB, и в ProPhoto, и в чём то еще.

dom1n1k
28.06.2016 16:42Конечно зависят. Об этом есть комментарий выше, и это подразумевается в тексте. Но видимо, нужно уточнить более явно, сейчас сделаю поправку.

Randl
28.06.2016 16:54Просто создается впечатление, что посыл поста — "это неправильные магические числа, замените их другими". По моему лучше было бы проверять цветовое пространство и делать соответствующий перевод, такой код даже после замены стандарта не будет работать неправильно, а максимум выдаст ошибку об отсутствие соответствующего преобразования..

dom1n1k
28.06.2016 17:16+2Формула не моя, её придумали задолго до меня :) И в настоящее время она определена как стандартная (тем же W3C). Я лишь хочу обратить на неё внимание.
Что касается разных пространств. Да, конечно, лучше и точнее считать всё по-взрослому. Но это сразу забросит нас в пучину нетривиальной и громоздкой колориметрической математики. Вот так быстро и сходу в ней разобраться сложно — да и не особо нужно, откровенно говоря. В 99% случаев, с которыми сталкивается рядовой программист, это себя не оправдает. Достаточно, чтобы он не использовал заведомо неправильные формулы, которые ему случайно нагуглились.
Ну а если кто-то решает более серьезные задачи — там, конечно, не обойтись. Но это отдельная и настолько большая тема, по ней пишут толстенные книжки, а не заметки на Хабр.
Randl
28.06.2016 17:24-2В 99% случаев визуальной разницей между двумя формулами можно пренебречь. Конечно, лучше и точнее считать по правильной формуле, но принципиальной разницы увидеть не удалось.

silvansky
28.06.2016 17:34Вообще, тут ещё от монитора зависит восприятие. Я тестировал на макбуке и внешнем монике Dell, на встроенном мониторе разница заметна слабее.

Randl
28.06.2016 17:59Ну у меня монитор хороший и калиброванный даже. Когда два изображения рядом, разница конечно заметна. Если встретить одно изображение где-то посреди статьи, никто и внимания не обратит.

dom1n1k
28.06.2016 17:43+4Какой-то радикальной, космической разницы — да, не будет.
Но зачем использовать заведомо неверные коэффициенты, если можно взять верные, и дополнительные трудозатраты для этого равны нулю? :)
amarao
28.06.2016 16:56+2А можно я задам глупый вопрос? Вот меня в курсе физики учили, что цвет определяется длинной волны. Которая меряется в нанометрах, или обратных к ним терагерцам.
А тут, вдруг, «координаты цветов». О чём речь, вообще? (Я понимаю, что это айтишные условности по перекладыванию байтиков из системы в систему, но, всё-таки).
dom1n1k
28.06.2016 17:07+7Метамерия. Цвет — это ощущение.
Если коротко, то длина волны однозначно соответствует цвету (и то с некоторыми оговорками) только в том случае, когда она одна — то есть имеем чистый спектральный свет. Если же имеем смесь волн (а на практике так почти всегда), ситуация резко становится намного сложнее.
Поэтому пришлось придумать свои особые, цветовые системы координат. Причем их много разных и у каждой свои плюсы и минусы.

alexkunin
28.06.2016 17:17+3Не спец, и ответ, возможно, тоже глупый.
Человеческий глаз не весь спектр различает, а три «диапазончика» — условно синий, зеленый и красный. А с точки зрения физики — есть просто длина волны. Чтобы одно соединить с другим, придумали цветовые модели цвета, воспринимаемого глазом.
Есть «человеческая» модель — LMS: ровно по колбочкам глаза все определено, зависимости неровные (заданы таблицей лукапов, так сказать). А есть историческая — XYZ (зависимости заданы формулами, т.е. можно рассчитать). Я бы тоже XYZ выбрал, чтобы не таскать везде таблицы значений.
Вот тут вся зубодробительность. По ссылке точные определения (формулы) координат.

lockywolf
28.06.2016 17:38>>О чём речь, вообще?
Если на пальцах:
На глаз падет электромагнитная волна, зависящая от времени. Это не синусоида!
Глаз не ловит конкретных отклонений волны, и он не спектроанализатор (это было бы слишком накладно).
Глаз делает две вещи: режет сигнал по типичному времени (времени реакции) и каждый интервал раскладывает в сумму ряда из всего трёх членов. У этих собственных членов есть собственные функции — это примерно (но не точно!) гауссианы с центрами в длинах волн, которые мы называем «красным», «синим» и «зелёным».
Очень много функций можно разложить так, что их скалярные произведения с гауссианами одинаковы. И спектроанализатор покажет разницу, а глаз — нет.

sasha1024
28.06.2016 17:17Когда-то в качестве развлечения делал игру. Стратежку. Там выдранные с какого-то сайта фришные картинки юнитов были в синей гамме. Чтобы получить картинки юнитов оппонентов, я делал «цветовой поворот» на 120° и 240° (т.е. R->G, G->B, B->R). Меня удивило, что цвета получались совсем неожиданные (из визуально-синей исходной картинки получались не визуально-красные, а какое-то сиреневые). Погуглил, понял что «мощности» каналов R, G и B неравны, стал подправлять их этими коэффициентами перед/после «поворота» (пробовал и sdtvWeights = [0.299, 0.587, 0.114], и hdtvWeights = [0.2126, 0.7152, 0.0722]). Визуально на моём мониторе с SDTV-коэффициентами выглядело лучше.
Ещё удивило, что gimp «поворачивает», кажется, вообще, без учёта коэффициентов. По крайней мере, в нём результат поворота получался совсем удручающий.
Randl
28.06.2016 17:26Цветовой поворот удобно делать в HSV, HSL и подобных.

sasha1024
28.06.2016 17:42Эмм, нет. При (стандартном) переводе из RGB в HSL/HSV как раз эти коэфициенты и не учитываются. Т.е. RGB=[0,0,255] даёт L=50% и RGB=[0,255,0] тоже даёт L=50% (несмотря на то, что [0,0,255] — это синий, а [0,255,0] — это салатовый).
Да и вообще, зачем мне HSL/HSV, если у меня поворот ровно на 120° и 240° — достаточно поменять местами каналы (ну, с поправками, учитывая, что разные каналы имеют разную «мощность»).
Вот для этих поправок и нужны коэфициенты. Прикол в том, что более древние (и по логике неправильные) SDTV-коэфициенты на моём мониторе давали более правильный результат, чем более новые, рекомендуемые в т.ч. автором этой статьи.
sasha1024
28.06.2016 17:56Возможно, я неправильно их называю SDTV- и HDTV-коэфициентами.
Вероятно, судя по статье, это YIQ и sRGB (накрайняк — NTSC и HDTV).
Но у меня в коде переменные почему-то были названы так.

Randl
28.06.2016 17:56Ну так у чисто зеленого и чисто синего одинаковая lightness. Менять надо hue, который в градусах и измеряется.

sasha1024
28.06.2016 18:00Ну так в том-то и дело, что #0000FF — это синий (не голубой), а #00FF00 — это салатовый (не зеленый). Т.е. #00FF00 визуально намного ярче, чем #0000FF.
Поэтому и нужны эти коэфициенты.
А если просто менять hue, то получится та же херня, что и в gimp'е.
playermet
28.06.2016 23:13> визуально намного ярче
Эта характеристика называется «светлота».
sasha1024
30.06.2016 00:43Стоп, подождите, Вы меня запутали.
Если светлота (lightness?) — это то, какой цвет визуально выглядит светлее…
… то как тогда называется третий параметр (L) в HSL?
playermet
30.06.2016 19:13Это он и есть. При L равном 100% в результате будет белый цвет, вне зависимости от остальных настроек. Просто L в HSL регулирует светлоту (близость к белому) без учета текущего тона (hue).

sasha1024
30.06.2016 19:39Ну так в том-то и дело, что #0000FF — это синий (не голубой), а #00FF00 — это салатовый (не зеленый). Т.е. #00FF00 визуально намного ярче, чем #0000FF.
Эта характеристика называется «светлота».
Тогда Вы сами себе противоречите. Я говорил о том, что #0000FF (синий) и #00FF00 (салатовый) в HSL имеют одинаковое L (50%) — несмотря на то, что #00FF00 визуально выглядит светлее #0000FF'а.
P.S.: Т.е. меня интересует «субъективная светлота» (не знаю как называется), а не параметр L в HSL.
playermet
30.06.2016 19:54> Тогда Вы сами себе противоречите
Не противоречу. Я лишь дал вам название термина.
> Я говорил о том, что #0000FF (синий) и #00FF00 (салатовый) в HSL имеют одинаковое L (50%) — несмотря на то, что #00FF00 визуально выглядит светлее #0000FF'а.
Именно это и называется «светлотой» (2).
> Т.е. меня интересует «субъективная светлота» (не знаю как называется), а не параметр L в HSL.
Объясню по другому. L в HSL отвечает за субъективную светлоту, но HSL не подразумевает что при одинаковом L она всегда будет одинаковой. В Lab эта же светлота, но формула устроена так что результативная светлота полностью определяется L.

sasha1024
28.06.2016 18:01Т.е. HSL/HSV тут никак не поможет (ну, я имею в виду, если не учитывать дополнительно эти коэфициенты, о которых речь в статье).
VioletGiraffe
28.06.2016 23:05Именно потому и недостаточно просто поменять каналы. По-моему, самое продвинутое цветовое пространство для манипуляций над воспринимаемыми цветами — Lab.

sasha1024
28.06.2016 23:21Ну, я просто умножал/делил на эти коэфициенты перед/после обмена каналов. Для той задачи этого хватило: картинки юнитов получились приемлемые (из нормально-синего танк не превращался в ярко-салатовый, и не вылазили посторонние цвета — если до «поворота» танк был в синей гамме, то после он был в красной/зелёной, а не фиолетовой/рыжей/другой).
Про Lab надо почитать, это интересно; просто для той задачи это было явно излишне.
Тут я просто отвечал человеку, который зачем-то настойчиво советовал HSL/HSV; и я ему пытался объяснить, что HSL/HSV мне не помог бы (HSL/HSV мне нужен был бы, если бы у меня был поворот не на 120° или 240° ровно, а на другое число; но поворот hue на 120° или 240° это и есть обмен каналов); так как проблему неравноценности RGB каналов сам по себе HSL/HSV бы никак не решал (потому что при стандартных формулах перевода RGB <-> HSL/HSV каналы как раз считаются равноценными), просто была бы лишняя арифметика.VioletGiraffe
28.06.2016 23:28Да, я всё понимаю — в том числе и что для той задачи ничего больше не требовалось. Просто я не так давно часа два изучал инфу о разных цветовых пространствах — есть идея сделать софтину для манипуляциями цветами, и хорошо бы это делать с учётом особенностей зрения человека. Пришёл к выводу, что Lab — единственный вариант, но там всё непросто с конвертацией. Вплоть до того, что я внятных формул для перевода из RGB не нашёл.

sasha1024
28.06.2016 23:50Странно, что этого ещё нету в стандартном gimp'е или ещё где-то. Потенциально низкое удобство пользования отдельной софтиной меня смущает. Возможно такие софтины уже есть, просто мы не знаем.
Ну, формулы RGB<->Lab я как раз нашёл, там (вроде) всё просто:
RGB<->sRGB<->«CIE XYZ»<->Lab
(1) RGB<->sRGB и sRGB<->«CIE XYZ»
(2) «CIE XYZ»<->Lab
(Но не знаю насколько просто всё остальное, потому что суть Lab я пока не понимаю.)
А какого рода софтину Вы собираетесь делать? Т.е. какой у неё должен быть функционал? (Условно говоря: просто преобразовать 1 цвет типа такого но сложнее или именно работа с изображениями?)VioletGiraffe
29.06.2016 00:00Спасибо! Википедию, конечно, я читал, (2) я находил, а (1) не смотрел (хотя и понимал, что это где-то задокументировано). Хотел прямое одноходовое преобразование, но хоть так.
Софтина именно для обработки изображений, конкретная задача, где нужен (ну или желателен) Lab — составление функции визуальной похожести цветов.

stepik777
28.06.2016 18:51+1А не нужно перед вычислением яркости сперва преобразовать sRGB к линейным координатам (то есть убрать гамму), а после опять применить её? Иначе получается, что результат будет зависеть от того, какая используется гамма в конкретном цветовом пространстве.

alexkunin
28.06.2016 19:25Тема зубодробительная, я могу ошибаться, но вы и правы, и не правы — одновременно.
Формула в статье — исключительно для sRGB. sRGB уже предполагает конкретную гамму — табличка в статье говорит «примерно 2.2». «Примерно» — это потому, что именно в sRGB гамма является функцией (вроде бы от яркости — для черного 1.0, для остального пространства — меняется от 1.0 до 2.4). Это ваше «не правы», на сколько я понимаю, т.к. пространство и его гамма фиксированы по определению.
Но, вроде, да, учитывать гамму нужно, и формула преобразования должна быть со степенями. Разница в абсолютных числах мизерна, а вот вычислений значительно больше — видимо, поэтому и не заморачиваются. Выше DistortNeo в своем комментарии привел ссылку на обоснование (там и формула). Это ваше «правы», и обоснование ваше верное — преобразование в линейное пространство (на сколько я понимаю, речь только о координате «яркость»).
stepik777
28.06.2016 19:45Понятно, что в sRGB гамма уже фиксированная. Но если взять другое цветовое пространтсво, например Rec. 709, в котором те же коэффициенты, но другая гамма, то рузультат будет выглядеть немного по другому, если не преобразовывать сперва в линейное пространство.

alexkunin
28.06.2016 20:05Тогда не понятно, в чем ваш вопрос состоит.
Прежде чем использовать коэффициенты, которые подходят только для sRGB, нужно преобразовать изображение в sRGB. Очевидно же.
DistortNeo
28.06.2016 20:04+1На самом деле плохо, что при работе с изображениями не заморачиваются с гаммой. И я имею в виду не только преобразование в YUV, но и использование алгоритмов обработки изображений в целом. Для многих задач игнор гаммы в угоду производительности не играет роли, но при работе с реальными изображениями, когда важна точность, гамму стоит учитывать.
Например, при гамме 2.2 смешение пикселей с интенсивностями 0 и 255 будет равно 186, а не 127.
dom1n1k
30.06.2016 23:23Эта гамма не дает мне покоя уже 2 дня. И вот я погрузился в справочники, провел кое-какие эксперименты и постепенно прихожу к выводу, что тут не всё так однозначно.
Эксперименты склонят меня к мысли, что для конвертаций (из пространства в пространство и в частности из rgb в grayscale) — гамму конечно же нужно учитывать.
Но для обработки изображений (например, регулировки яркости, контрастности, фильтры, смешивание и пр.) гамму лучше не трогать. Она же не просто так придумана — она нужна, чтобы сделать шкалу перцептивной. И гамма sRGB и L* делают это с разной степенью точности. Цвета нужно смешивать по перцептивной шкале, а не физической.
Я пока поостерегусь назвать эти выводы окончательными. Но похоже, что ФШ именно так и поступает.
И похоже, что мой апдейт 2 нужно проапдейтить, рассуждения в нём были частично ошибочные.
DrSmile
01.07.2016 00:57Всякую артистическую обработку можно проводить в нелинейном пространстве. Однако трансформации, имеющие конкретный физических аналог (смещения, изменения масштаба, повороты, в том числе нерегулярные; фильтры размытия и т. п.) обязаны быть реализованы физически корректно. В противном случае будут артефакты той или иной степени заметности в местах с сильными градиентами. Например, при движении тонкой линии, ее яркость будет заметно колебаться.

dom1n1k
01.07.2016 13:57А что означает «физически корректно»? Ведь (не)линейность пространства — штука относительная.
CIE Lab и любое гамма-корректированное RGB-пространство очень нелинейны (типичный показатель степени от 1.8 до 3) относительно CIE XYZ. Но относительно человеческого восприятия всё наоборот — они более линейны (для того гамма и придумана!), Lab получше, RGB похуже. Но оба они превосходят в этом смысле XYZ, которое очень сильно нелинейно (эллипсы МакАдама).
XYZ это такая математическая абстракция, которую придумали для удобства математики в докомпьютерную эпоху — считали все на логарифмических линейках, и отрицательные числа доставляли большие неудобства. Но оно вообще не перцептивное. Так почему же обработка в нём (или в его линейных преобразованиях, которыми являются RGB-пространства без гамма-коррекции) должна быть более корректна?
Jetmanman
10.11.2016 13:11-8Не все понял. Но возможность путешествия во времени не создает противоречий и логически возможно, другое дело какие здесь ограничения из физики. Судьба существует, я об этом писал в своей статье https://geektimes.ru/post/279780/, а то, что людям не хочется думать, что судьба есть это лишь их желания так думать. Вы сами написали почему судьба есть, но начинаете выдумывать почему ее может не быть. И вот еще что скажу, люди не понимают, что прошлое также существует как настоящее и будущее, это можно доказать из существования парадокса близнецов например, когда один близнец молоде другого и соответственно видит будущее второго близнеца. В реальности вместо близнецов есть космонавты, которые возвращаясь на землю чуть моложе остальных людей, т.е. находятся в их будущем. А в той своей статье я еще писал можно ли предсказать будущее.

dom1n1k
01.07.2016 14:54Я как-то участвовал в подобной дискуссии на форуме rudtp, только там было всё наоборот :) Человек утверждал, что корректная интерполяция цветов обязана быть максимально перцептивна (т.е. всегда проводиться только в пространстве Lab).
Ошибка ваших рассуждений в том, что Y — это не физическое количество света. Потому что XYZ это тоже пространство «цветовых ощущений», а не физического количества фотонов.
DrSmile
01.07.2016 17:16XYZ пространство однозначно и физическо корректно определяется через количества фотонов. Есть 3 функции спектральной чувствительности, которые фотону определенной частоты ставят в соответствие тройку {X, Y, Z}. С точки зрения математики, базис XYZ — это трехмерное подпространство исходного бесконечномерного пространства физического цвета.
В контексте обсуждения важно, что это подпространство линейное, т. е. подчиняется принципу суперпозиции. Соответственно, если взять два источника света и посветить на одно место, то итоговой цвет будет суммой цветов источников в любом линейном пространстве (а уже конкретно ли это XYZ, RGB, или, вообще, функция от длины волны, не важно).
tretyakovpe
10.11.2016 16:35не вижу в условии угла падения 90 градусов.
на картинке в посте вижу «пилу» отраженного луча. вот эта «пила», продлённая в бесконечность и становится лучом видимо
DrSmile
01.07.2016 20:53Это все линейные преобразования, на работоспособность принципа суперпозиции не влияют. Проблемы там возможны только при нелинейных операциях, например, при освещении поверхности источником умножается спектральная интенсивность на коэффициент поглощения, и делать это в «урезанных» цветовых координатах (XYZ или RGB) не совсем точно.
В общем, лучше один раз увидеть. Тонкие линии на разном сабпиксельном смещении
без учета гаммы: с учетом:
с учетом:
Невооруженным глазом видны колебания яркости в первом случае.
(Картинки из темы на геймдеве, посвященной антиалиасингу.)
rerf2010rerf
10.11.2016 16:49Бабло получили, попили, договор всё равно не подписали, соответственно ничего не построили…

DrSmile
01.07.2016 22:05Субпиксельные эффекты — это не особый, а всего лишь частный случай наложения цветов. Какой-нибудь дефокус или наложение света от разных источников будут действовать точно так же.
А субъективные вопросы они на то и субъективные, чтобы не иметь однозначного ответа. Например, моя тренированная физическая интуиция говорит за нижний квадрат. Поэтому я предпочитаю обсуждать только объективные вопросы.
НапримерКакой средний цвет будет у шахматки на большом расстоянии?

Или вот мой прошлый пример с яркостью цветов

Без учета гаммы зеленый должен быть ярче красного в полтора раза, с учетом — красный немного ярче зеленого.
dom1n1k
02.07.2016 01:57C красно-зеленым примером уже раньше разобрались. А что касается остального:
Мой пример.
Мое мнение — самый верхний. Но это моё, оно теоретически может быть предвзято. Я ещё опросил 4-х человек (никто их них не понимает значения букв на картинке). Двое сказали что средний квадратик, один что верхний, а еще один, что он бы еще немного затемнил верхний.
Шахматка.
На десктопе совпадает с верхним. На планшете и телефоне где-то посередине, но чуть ближе к нижнему. Сторонние мнения: у одного ближе к нижнему, у одного ближе к верхнему, у одного точно совпал с нижним.
И можно было бы списать разброс на разные калибровки разных экранов, но… два последних человека (с противоположным виденьем) смотрели на одном компьютере :)

DrSmile
02.07.2016 03:22У всех ЖК экранов сильно плавает цветопередача в зависимости от угла, особенно вертикального. Еще некоторые устройства отображения бывают испорчены разными «улучшайзерами» (у меня проектор этим грешит и приходится делать квадраты шахматки побольше, чтобы компенсировать эффект). Плюс, условия эксперимента необходимо понимать буквально: надо не субъективно оценивать похожий цвет, а отойти на такое расстояние, с которого квадраты перестанут быть различимы.
Но, вообще, все это лирика и законы физики предполагают только один ответ. Получение другого говорит о неправильной калибровке монитора и/или неправильной постановке эксперимента.
DistortNeo
01.07.2016 09:33Для фотореалистичной обработки гамму учитывать нужно. Гамма придумана для того, чтобы сделать более-менее равномерным распределение отсчётов шкалы в соответствии с человеческим восприятием.
Например, черный провод на белом фоне после размытия должен пропать, а белая нить на чёрном фоне — стать толще, почти не потеряв в яркости. Без преобразования гаммы оба объекта бы стали серыми.
dom1n1k
01.07.2016 13:23Это почему так должно? Имею в виду пример с нитью.
DistortNeo
01.07.2016 14:08Потому что именно так и происходит в реальном мире.

dom1n1k
01.07.2016 15:01Где-то можно почитать более подробное объяснение и обоснование этого феномена?

homm
28.06.2016 22:08Добью вас про линейность цветового пространства. Вообще говоря перевод sRGB > RGB не ограничивается выправлением гаммы. Формула чуть сложнее.

dom1n1k
28.06.2016 22:13Не совсем понял, на что конкретно обращать внимание. На то, что график гаммы в sRGB состоит из двух кусков, линейного и степенного? Это я знаю. Или что-то еще?

sasha1024
29.06.2016 00:25Вообще, во 2-м update'е он как раз считает по более сложной формуле (если я правильно понял).
Но за хорошую ссылку спасибо.

TheShock
29.06.2016 02:19+1А я вообще использовал когда-то
(3r+6g+1b)/10. Визуально разницы почти не заметно, особенно в динамике.
Randl
29.06.2016 16:28Ну так относительная яркость — это всего лишь один из способов перевода изображения в ч/б. Иногда можно вообще один канал взять и готово, иногда надо изображение сначала обработать до перевода в ч/б. У Маргулиса про это хорошо написано, правда, конечно, в свете ручной обработки а не автоматической.

littleguga
29.06.2016 10:59У Вас ссылка на Chart.js битая.
По хорошему там везде надо issue открыть или кинуть pull request, но как аргументировать?
dom1n1k
29.06.2016 11:16Видимо они изменили систему сборки, потому что папка dist вообще пропала из ветки master. Но если скачать библиотеку со странички релизов — там всё на месте (Chart.js#L450). Но поскольку в их исходниках это место теперь не находится, это вероятно на самом деле тянулось из библиотеки третей стороны?

darkRabbit
29.06.2016 14:52Это библиотека github.com/chartjs/color, форк github.com/harthur/color, ноги которой растут из библиотеки github.com/brehaut/color-js (в которой, кстати, всё с этим хорошо: github.com/brehaut/color-js/blob/master/color.js#L271).

PaulZi
29.06.2016 12:45Я помню сталкивался с этим, когда занимался конвертацией в AviSynth. Я на сколько я помню, там была такая рекомендация:
использовать BT.601 — для старых не-HD источников (DVD и т. п.)
использовать BT.709 — для HD-видео
Не помню уже, откуда инфа, и на сколько она верна, но в памяти отложилось именно так.
dom1n1k
29.06.2016 12:56+1По факту выходит, что BT.601 верны только для американского NTSC до 1987 года и японского всех лет (японцы не переходили на новую спецификацию) и PAL/SECAM до 1970 года.
Для всего остального BT.709 будет лучше — более свежие версии NTSC/PAL/SECAM хоть и не соответствуют им в точности, но очень близки.

iroln
29.06.2016 13:49Посмотрел в scikit-image. Они используют вторую формулу.
The weights used in this conversion are calibrated for contemporary CRT phosphors
Ссылаются на этот документ.

vconst
29.06.2016 16:41+1Я не программист, я фотошопер. Из своего опыта могу сказать, что правильный десатурейт должен не просто приводить все к определенной яркости, но еще и разделять цвета.
Все у кого есть под руками фотошоп, могут проверить два метода:
1) Создать RGB-изображение, залить фон градиентом радуги, применить к нему корректирующий слой Hue/Saturation в режиме наложения Normal и сдвинуть ползунок насыщенности в крайнее левое положение. Получится эффект команды Desaturate, аналогичный большинству аналогичных алгоритмов. Но картинка выйдет серая и плоская
2) Повторить все шаги, но корректирующему слою сделать режим наложения Color. Получается Ч/Б картинка совсем другого характера, даже без цвета она остается яркой и контрастной, все цвета максимально разделяются один от другого
Я не могу проверить описываемые в статье алгоритмы на своей картинке, но вот результат получающийся в фотошопе (прошу прощения, но полноценная работа с тегами мне недоступна, потому длинные текстовые ссылки):
Цветной исходник: www.dropbox.com/s/mxbr7fpos67xme6/rainbow-color.jpg?dl=0
Ч/б результат в режиме Normal: www.dropbox.com/s/oeky5jgi3wtncmh/rainbow-bw-normal.jpg?dl=0
Ч/б результат в режиме Normal: www.dropbox.com/s/j90vgvi77c9n79k/rainbow-bw-color.jpg?dl=0
Будет здорово, если кто нибудь десатурнет цветной исходник по обсуждаемым алгоритмам и покажет результат, для сравнения с фотошопным
dom1n1k
29.06.2016 17:17Команда Desaturate в ФШ работает в координатах HSB, поэтому её результат и получается, очень мягко говоря, сомнительный (я бы не использовал его вообще).
Самый точный и правильный (с инженерной точки зрения) вариант обесцвечивания — это перевести картинку в Lab и взять канал L (lightness).
Mode > Grayscale по качеству где-то посередине (не идеально, но для большинства случаев достаточно).
vconst
29.06.2016 17:42+2Не согласен.
Я рассуждаю не как программист, а как ретушер-цветокорретор. Картинка должна быть не просто «правильная» с точки зрения математики, она должна быть яркой и контрастной, с минимальными потерями в деталях – то есть она должна быть красивой. А это не алгоритмизируется так просто
Вот примеры той же радуги:
L-канал из режима Lab: rainbow-Lab.jpg
Командой Grayscale: rainbow-gray.jpg
Если сравнить все варианты – то самый детализированный, то есть тот, у которого цвета максимально разделены друг от друга – десатурнутый с режимом наложения колор. У изображения есть не только детализация по пикселям, но и цветовая, я сейчас о ней и говорю. Пока обсуждаются абстрактные цветные квадратики, все это не наглядно, но когда приходится работать с реальной фотографией, то разница становится заметна и понятна
На самом деле все еще сложнее, грамотно перевести картинку в чб можно только с помощью команды Calculation, пробуя накладывать разные каналы друг на друга, в разных режимах и пропорциях, это сложная задача и после нее все равно придется доводить картинку корректирующими кривыми, но двухкликовый способ лучше всего тот, который я описал, Я плохо представляю, как его запрограммировать, хотя предполагаю, что это возможно, потому что наблюдал подобные задачи и их решения программными методами как на сервере, так и в браузере. Я не вспомню навскидку, но мне кажется, что в CSS есть возможность сделать подобную обработку не простым обесцвечиванием, а с наложением в разных режимах.
Я всего лишь добавил в чисто математический разговор, рассуждения о цвете профессионала-полиграфиста, который почти 20 лет занимается цветокоррекцией. Может это кому то окажется полезным, потому что, как показывает практика, мало кто представляет себе реальный процесс обработки изображений для глянцевых журналов, в инете этому уделяется куда меньше внимания, хотя бы потому, что разброс экранов по качеству и искажениям несравнимо больше, чем в полиграфии и многое прощается
dom1n1k
29.06.2016 18:20Я разобрался. Запрограммировать его сравнительно несложно. Адобовская документация говорит:
Color Creates a result color with the luminance of the base color and the hue and saturation of the blend color. This preserves the gray levels in the image and is useful for coloring monochrome images and for tinting color images.
При смешивании берется яркость от нижнего слоя и тон с насыщенностью от верхнего. Насыщенность равна нулю, тон в этих услових не определен и потерял смысл. То есть способ действительно достает из картинки яркостный канал, хотя и окольным путем. Фактически, обходится врожденный порок функции desaturate, которая работает в не-перцептивных координатах и потому полностью всё корёжит (когда я писал, что не советую её использовать — я имел в виду в чистом виде).
Вопрос только, что в точности они подразумевают под luminance. Скорее всего это нечто похожее на формулу, описанную в посте, но остается вопрос настроек (конкретные коэффициенты, учет гаммы и т.п.)
vconst
29.06.2016 18:36Можно чисто эмпирически выяснить, что они имеют в виду под luminance, измерив яркость пикселей пипеткой в фотошопе и посчитать, какое получается значение. Свойство из CSS «background-blend-mode» – подойдет? В описании сказано, что там аналоги наложений в фотошопе

Randl
29.06.2016 21:11luminance — это L канал из HSL. Подробнее здесь.

dom1n1k
29.06.2016 21:20+1В HSL вообще-то lightness.
И более того, продукты Adobe никогда не были замечены в связях с моделью HSL, они предпочитают HSB/HSV.
Randl
29.06.2016 21:31Упс, и правда. Канал B из HSB, наверное первая буква в luminance меня сбила. Но вы лучше по ссылке перейдите, там все подробно и с примерами.

vconst
29.06.2016 23:36Забавный дядька, знает то он много, но скорее из разряда «кто не умеет работать — учит»

littleguga
02.07.2016 03:26Кстати, я обратил внимание и в inkscape всё верно, ибо там помечено, что это для NTSC.


alexkunin
Очень не хватает примера: исходная цветная картинка, ч/б по старой формуле, ч/б по новой формуле.
alexkunin
Вот фиддл с Леной: http://jsfiddle.net/x6W4C/2/. Разница есть, на глаз ощутима, но не принципиальна. На каком-нибудь другом изображении может и получше было бы видно.
degorov
В тёмной части спектра разница вполне заметна даже так.
petrovnn
Объясните тогда, почему в grayscale, слева как раз более однородно?
dom1n1k
Мой вариант
Нужно выяснять чем и как конвертировали в grayscale, какие настройки и т.д.
Случайно не функцией Desaturate в ФШ? Она работает иначе — в модели HSB (т.е. совершенно не перцептивно).
bertmsk
Тогда ценность багета автора резко упадет, поскольку картинки практически идентичные
Исходная:
/>
Со старыми коэффициентами
/>
С новыми коэффициентами
/>
DistortNeo
Кстати, формула все равно неверная: при вычислении Y нужно учитывать гамму.
Вот статейка, где можно посмотреть результаты:
www.cgm.computergraphics.ru/files/cgm/rgb2gray_article.pdf
dom1n1k
Я начал было писать ответ про гамму, но он получился такой большой, что я его тоже вынес в апдейт.
dom1n1k
См. апдейт
alexkunin
Все вы верно в апдейте написали. Но! Нет прямого и простого примера. В вашем кодепене случайные цвета немного отличаются (и так как они случайны, разница эта на глаз не видна — нужно комплексное изображение, чтобы глаз распознал контент и увидел различия), и это не привносит ясности: все еще нет примера, демонстрирующего видимую, ощутимую разницу. Да, оценка этой разницы весьма субъективна (большинство, наверное, выбрало бы более контрастный вариант, т.к. «ну четче же»), и к правильности отношения не имеет.
Я бы так написал в статье: «вот пример изображения — до, после старой формулы, после новой; как видите, разница есть, хоть и невелика, но хочу обратить ваше внимание, что...» — дальше ваш пассаж про правильность.
Просто без этого ваша статья о переводе цветных изображений в черно-белые осталась без изображений, т.е. «теоретическое махание руками» (как если бы где-то на природе человек без бумажки и карандаша буквально на пальцах что-то пытался пояснить — но мы ж не на природе, в нашем распоряжении любые инструменты). С точки зрения науки все верно. С точки зрения «заинтересовать читателя» — нужны примеры, без которых средний читатель останется неудовлетворенным.
sasha1024
Совет: я бы модифицировал Ваш пример следующим образом (но мне лень)…
У Вас (псевдокод):
var ethalonY := 0.5, count := 100;
for (var n := 0; n!=count; ++n) {
var r := random(), b := random();
var g1 := getGreenFromRedBlueY(r, b, ethalonY, [0.299, 0.587, 0.114]);
var g2 := getGreenFromRedBlueY(r, b, ethalonY, [0.2126, 0.7152, 0.0722]);
putLeft(r, g1, b); putRight(r, g2, b);
}
Надо:
var ethalonY := 0.5, count := 100;
for (var n := 0; n!=count; ++n) {
var h := n / count * 360°;
var (r, g, b) := hslToRgb(h, 100%, 50%);
var (r1, g1, b1) := normalizeToY(r, g, b, ethalonY, [0.299, 0.587, 0.114]);
var (r2, g2, b2) := normalizeToY(r, g, b, ethalonY, [0.2126, 0.7152, 0.0722]);
putLeft(r1, g1, b1); putRight(r2, g2, b2);
}
Т.е.:
1. Не подбирать зелёный по красному и синему, а подбирать все 3 канала по hue.
2. Меньше рандома, просто перебрать все значения hue подряд с каким-то шагом.
sasha1024
А ещё лучше: не слева одна картинка, справа другая, а отобразить получившиеся цвета в виде 2 рядов один под другим:
???????????????????????????????????????????????????????????????????????????????? (YIQ)
???????????????????????????????????????????????????????????????????????????????? (sRGB)
Какой ряд равномернее по яркости — тот и лучше.
dom1n1k
Такое расположение больше подходит для сравнения пар цветов между двумя группами.
Но нам ведь важнее смотреть на однородность группы, т.е. как раз лучше показать её сбитой в кучу, а не вытянутой колбасой.
sasha1024
Может быть, это всё субъективно, мне кажется, так было бы лучше, но, может быть, я неправ.
Мой основной коммент был выше про «не G по (R:=rand(), B:=rand(), Y:=0.5), а L по (H:=seq(), S:=100%, Y:=0.5)».
dom1n1k
Эмм… не получится же: координата L в HSL и Y в XYZ — это разные параметры. По смыслу немного похожие, но разные.
sasha1024
А где я говорил, что они одинаковые?
dom1n1k
Тогда я не совсем понял, какие преимущества сулит предложение. Лучше форкнуть и показать как надо :)
DrSmile
Как уже неоднократно писали, учет гаммы так же важен, как и цифры интенсивности. Так что «рядовой программист», в итоге, все равно сделает неправильно, без учета нелинейности цветового пространства, независимо от того, какие магические числа он нагуглит. Не позорьтесь, исправьте в апдейте
dom1n1k
См. второй апдейт
DrSmile
Очевидно, что написанное там не соответствует истине.
Пусть у нас есть два цвета — красный {1, 0, 0} и темно зеленый {0, 0.5, 0} в нелинейном цветовом пространстве с гаммой 2.2. Забив на гамму и применяя формулу напрямую, получим яркости 0.2126 и 0.3576. Если же корректно преобразовать цвета в линейное пространство, рассчитать яркость и вернуть в нелинейное, то получится 0.4947 и 0.4293. Налицо принципиальное изменение отношения.
Вообще, если пытаться приближать правильную формулу без степеней, то стоит хотя бы возвести в степень 1/2.2 сами коэффициенты, т. е. использовать Y = 0.4948R + 0.8587B + 0.3028G. Будет работать правильно хотя бы для чистых цветов. Для смешанных, в том числе белого, будет врать, поэтому надо заново нормировать на единицу. В общем, как я и говорил, «рядовой программист» будет врать независимо от выбранных магических чисел.
dom1n1k
Нашел у себя ошибку в выкладках, касающуюся этого момента. Но исследовать её буду уже завтра.
dom1n1k
Поэкспериментировал я с Монте-Карло — генерировал рандомные пары цветов и проверял, в каком количестве случаев отношение яркости сохранятся при разных методах. За эталон принимал соотношение CIE L*.
Результаты вполне устойчивые, разные эксперименты дают разброс <0.1%.
Выводы в общем-то капитанские: влияет и то, другое. Разница лишь в том, что гамма просаживает производительность, а коэффициенты достаются бесплатно.