В статье речь пойдет о построение нейронных сетей (с регуляризацией) с вычислениями преимущественно векторным способом на Python. Статья приближена к материалам курса Machine learning by Andrew Ng для более быстрого восприятия, но если вы курс не проходили ничего страшного, ничего специфичного не предвидится. Если вы всегда хотели построить свою нейронную сеть с преферансом и барышням векторами и регуляризацией, но что то вас удерживало, то сейчас самое время.
Данная статья нацелена на практическую реализацию нейронных сетей, и предполагается что читатель знаком с теорией (поэтому она будет опущена).
Код откомментирован на английском, но вряд ли у кого-то будут сложности, так как основные комментарии даются также в статье на русском.
Мы будем писать код для поиска оптимальных значений весов с помощью scipy.optimize.fmin_cg, а так же самостоятельно, поэтому скрипты будут универсальными.
Мы сразу перейдем к практике, о нейронных сетях есть много статей на Хабре,
Программное обеспечение и зависимости
Python 3.4 (на 2.7 тоже будет работать с небольшими правками)
Numpy
SciPy (опционально)
Для удобства работы все функции нейронной сети вынесем в отдельны модуль network.py
Первое что требуется реализовать это создание полносвязанной нейронной сети. Фактически это значит что нам необходимо иницилиазовать матрицы весов Theta ? рандомными значениями от -1 до 1.
Так как мы создаем функции внутри класса network, функция будет фактически иметь одну переменную layers, которая содержит количество слоев и нейронов в создаваемой сети в формате list. Например [10, 5, 5, 1] означает сеть с десятью входными нейронами, двумя скрытыми слоями по 5 нейронов каждый и выходным слоем с одним нейроном
Так как размер переменной layers вряд ли будет превышать несколько десятков элементов даже в самой сложной нейронной сети, в этом случае применим цикл for.
В результате мы хотим получить list theta элементы которого будут матрицами с весами.
На данном этапе нам необходимо посчитать выходной сигнал нейронной сети используя веса инициализированные на предыдущем шаге.
Кратко говоря, с помощью команды np.vectorize функция теперь может принимать и считать матрицы значений. Например, для каждого элемента матрицы 10х1 будет посчитана логистическая функция, и возвращена матрица значений размерностью 10х1
Из важного хочу заметить, что мы добавляем столбец биаса после того, как применили активационную функцию к сумме произведений. Это значит что биас всегда равен единице, а не логистической функции от единицы (что есть 0,73)
Кроме того, в финальной матрице активационных функций биас присутствует во всех слоях, кроме выходного слоя, в нём находятся только выходные сигналы нейронной сети (соответственно размерность матрицы = количество примеров*количество нейронов в выходном слое).
Для тех, кто не близко знаком с питоном отмечу, что в функцию runAll передаются не копии переменных (например сама нейронная сеть nn) а ссылки на них, поэтому когда мы изменяем переменную nn[‘z’] = z мы изменяем нашу сеть nn несмотря на то, что не передаем переменную nn обратно.
В результате данная функция (runAll) вернет нам матрицу выходных сигналов сети (её размерность количество выходных нейронов*1) и изменит матрицы z и a в переменной нейронной сети.
Ошибка выходного сигнала нейронной сети с регуляризацией считается по следующей формуле
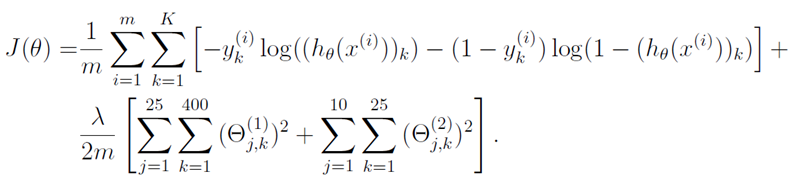
Картинка взята из материалов курса Machine Learning
m – количество примеров, K – количество выходных нейронов нейронной сети, h0(xi) – вектор выходных значений нейронной сети, ? — матрицы весов, где ?^1 матрица весов для первого скрытого слоя, lambda – коэффициент регуляризации.
Если она кажется вам довольно страшной и непонятной, это нормально :), в сущности, она раскладывается на 2 составные части, с которыми мы будем работать.
Подробное и понятное объяснение сути этой формулы растянется, и я не уверен, что оно нужно для такой подготовленной публики, поэтому пока опустим его, но пишите, при необходимости добавлю.
Собственно функция ошибки возвратит нам единственное значение в формате float, которое будет характеризовать насколько правильно наша нейронная сеть вычисляет выходной сигнал.
Функция возвращает ошибку нейронной сети для данной матрицы X входящих параметров.
Подсчитываем первую часть формулы, непосредственно ошибку сети
Считаем регуляризацию
Допускаем цикл по массиву с матрицами theta так как предполагается что у нас весьма ограниченное количество слоев, производительности не будет нанесен большой урон.
Удаляем из регуляризации связь с биасом так как он вполне может принимать большое значение, если нам надо сильно сдвинуть логистическую функцию по оси Х.
На этом этапе мы можем создать нейронную сеть, посчитать выходной сигнал и ошибку, теперь необходимо только вычислить градиент и реализовать алгоритм коррекции весов.
На этом шаге нам не обойтись без цикла по входящим векторам и для того, что бы немного ускорить расчет градиента, мы выносим максимум операций перед циклом. Например на предыдущих шагах мы специально спроектировали функцию runAll таким образом что бы она вычисляла матрицу входных значений, а не вектора (строки) поштучно, на этом этапе мы заранее рассчитаем выходные значения, затем будем обращаться к ним в цикле. По экспериментальным замерам данные фичи ускоряют функцию дополнительно на 25%
Мы используем обратный цикл по слоям нейронной сети от последнего к первому, так как нам надо вычислять ошибку и передавать её на слой назад, что бы вычислять следующую и т.д.
Основная сложность состоит в том, что бы не запутаться в индексах переменных. Например в большинстве документации по нейронным сетям для к примеру трехслойной сети (с одним скрытым слоем), дельта ошибки выходного слоя будет иметь индекс 3, понятно, что в этом случае лист должен состоять из четырех элементов, при этом лист градиентов состоит из 3 элементов.
Функция возвращает лист элементы которого являются матрицами, размерности которых совпадают с размерностью матриц theta
При этом данная функция лямбда, это ни что иное как производная от активационной функции (сигмоида), поэтому если вы хотите заменить активационную функцию меняйте еще и производную
Теперь мы можем протестировать нашу нейронную сеть и даже попробовать её обучить чему нибудь :)
Для начала научим нашу сеть простой сегментации, все значения в пределах [0;5) это нуль, [5;9] это единица
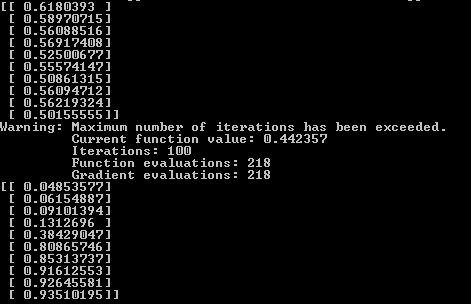
Результат. Вывод нейронной сети до тренировки, тренировка и после тренировки. Видно, что после тренировки первые пять значений ближе к нулю, вторые пять ближе к единице.
В предыдущем примере обучение контролировала функция fmin_cg теперь же мы будем менять theta(веса сети) самостоятельно.
Поставим простую задачу, отличать восходящую тенденцию от нисходящей. Нейронной сети на вход будут подаваться 4 числа, если они последовательно увеличиваются, это единица, если уменьшаются, это нуль.
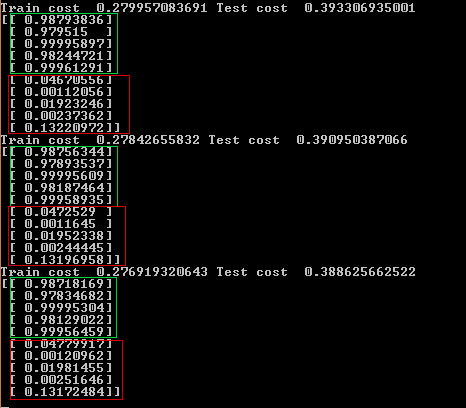
Спустя 400 итераций (примерно 1 мин.) по каким то причинам у последнего тестового примера самая высокая ошибка (выход нейронной сети 0.13), скорее всего в этом случае для повышения качества помогло бы добавить тренировочные данные.
В цикле изменяем theta для того, что бы добиться максимального результата. Получается, что мы как бы скользим к локальному минимуму функции (а если бы мы добавляли градиент, то мы шли бы к локальному максимуму). Переменная alf часто называемая «скоростью обучения» отвечает за то как сильно мы будем изменять theta в каждой итерации. При этом если вы установите параметр альфа слишком большим, ошибка сети может даже увеличиваться или прыгать вверх и вниз так как функция будет просто перешагивать локальный минимум.
Как видно, вся нейронная сеть состоит из одной переменной типа dict, поэтому её легко серрилизовать, и сохранить в простом текстовом фале и так же восстановить для дальнейшего использования.
Возможно следующая публикация будет на тему как еще ускорить данный код (и любой другой, написанный на Python) с помощью вычислений на GPU
UPD
Спасибо всем, кто плюсует.
Данная статья нацелена на практическую реализацию нейронных сетей, и предполагается что читатель знаком с теорией (поэтому она будет опущена).
Код откомментирован на английском, но вряд ли у кого-то будут сложности, так как основные комментарии даются также в статье на русском.
Мы будем писать код для поиска оптимальных значений весов с помощью scipy.optimize.fmin_cg, а так же самостоятельно, поэтому скрипты будут универсальными.
О каких векторах речь и зачем они нужны?
Предположим простую задачу сложить попарно элементы двух одномерных массивов. Мы можем решить эту задачу в цикле с перебором всех значений массивов или сложить два вектора. Рассмотрим следующий код.
На простом ноутбуке цикл в среднем обрабатывается за 4 сек. 40 мил. сек. Вектора складываются за 0.02 сек.
Примерно такая же разница в скорости и при других арифметических операциях. Не говоря уже о наглядности кода.
import numpy as np
import time
A = np.random.rand(1000000, 1) # Создаём вертикальный вектор 1 млн. строк и 1 столбец с рандомными числами float
B = np.random.rand(1000000, 1) # ----
C1 = np.empty((1000000, 1)) # Создаём вертикальный вектор 1 млн. строк и 1 столбец с пустыми значениями
C2 = np.empty((1000000, 1)) # Создаём вертикальный вектор 1 млн. строк и 1 столбец с пустыми значениями
start = time.time()
for i in range(0, len(A)):
C1[i] = A[i] * B[i] # Складываем каждый элемент векторов A, B и записываем сумму в соответствующую строку вектора C
print(time.time() - start)
start = time.time()
C2 = A + B #Складываем два вектора напрямую
print(time.time() - start)
if (C1 == C2).all(): # Проверяем на равенство все значения массивов
print('Equal!')
На простом ноутбуке цикл в среднем обрабатывается за 4 сек. 40 мил. сек. Вектора складываются за 0.02 сек.
Примерно такая же разница в скорости и при других арифметических операциях. Не говоря уже о наглядности кода.
Мы сразу перейдем к практике, о нейронных сетях есть много статей на Хабре,
например эти
Программное обеспечение и зависимости
Python 3.4 (на 2.7 тоже будет работать с небольшими правками)
Numpy
SciPy (опционально)
Для удобства работы все функции нейронной сети вынесем в отдельны модуль network.py
Создание сети
Первое что требуется реализовать это создание полносвязанной нейронной сети. Фактически это значит что нам необходимо иницилиазовать матрицы весов Theta ? рандомными значениями от -1 до 1.
Так как мы создаем функции внутри класса network, функция будет фактически иметь одну переменную layers, которая содержит количество слоев и нейронов в создаваемой сети в формате list. Например [10, 5, 5, 1] означает сеть с десятью входными нейронами, двумя скрытыми слоями по 5 нейронов каждый и выходным слоем с одним нейроном
def create(self, layers):
theta=[0]
for i in range(1, len(layers)): # for each layer from the first (skip zero layer!)
theta.append(np.mat(np.random.uniform(-1, 1, (layers[i], layers[i-1]+1)))) # create nxM+1 matrix (+bias!) with random floats in range [-1; 1]
nn={'theta':theta,'structure':layers}
return nn
Так как размер переменной layers вряд ли будет превышать несколько десятков элементов даже в самой сложной нейронной сети, в этом случае применим цикл for.
В результате мы хотим получить list theta элементы которого будут матрицами с весами.
Почему мы инициализируем theta[0] = 0 ?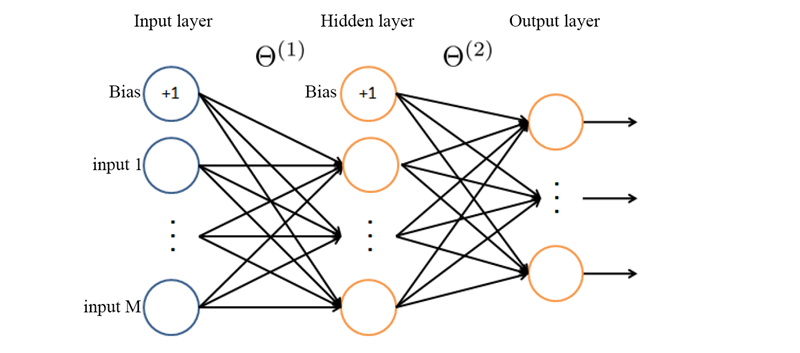
Картинка из материалов курса Machine Learning, с доработками
В области нейронных сетей принято называть ?1 матрицу весов от входных данных (input) до первого нейронного слоя. Так как у нас нет никаких слоев до Input layer, то нулевой матрицы весов тоже нет.

Картинка из материалов курса Machine Learning, с доработками
В области нейронных сетей принято называть ?1 матрицу весов от входных данных (input) до первого нейронного слоя. Так как у нас нет никаких слоев до Input layer, то нулевой матрицы весов тоже нет.
Что представляет из себя theta[1], theta[2], …, theta[n] ?
Все матрицы составляются по одному алгоритму, поэтому рассмотрим theta[1] для примера. Theta[1] это матрица в которой количество строк равно количеству нейронов в первом скрытом слое, а количество столбцов равно столбец для биаса (смещения) + количество нейронов во входном слое.
То есть если мы возьмем первую строчку матрицы theta[1] то нулевой элемент (читай нулевой столбец) будет соответствовать весу биаса, остальные элементы (столбцы) будут соответствовать весам для связи с каждым элементом входящего слоя.
То есть если мы возьмем первую строчку матрицы theta[1] то нулевой элемент (читай нулевой столбец) будет соответствовать весу биаса, остальные элементы (столбцы) будут соответствовать весам для связи с каждым элементом входящего слоя.
Что такое Bias (биас) и зачем он нужен?
Bias переводится с английского «смещение» и фактически это он и означает (всегда ваш, Кэп). Лучше чем здесь я вряд ли скажу, поэтому просто выполню перевод.
Биас полезен почти всегда так как позволяет смещать функцию активации влево или вправо, что может быть крайне важно для успешного обучения.
Простой пример поможет понять. Представим простейшую нейронную сеть без скрытого слоя, только один входящий и 1 исходящий нейрон
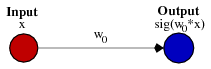
Выходной сигнал нейронной сети подсчитывается умножением веса W0 на сигнал X и применением активационной функции (чаще всего сигмоид) к произведению.
Пример функций, которых мы получим при разных значениях веса W0
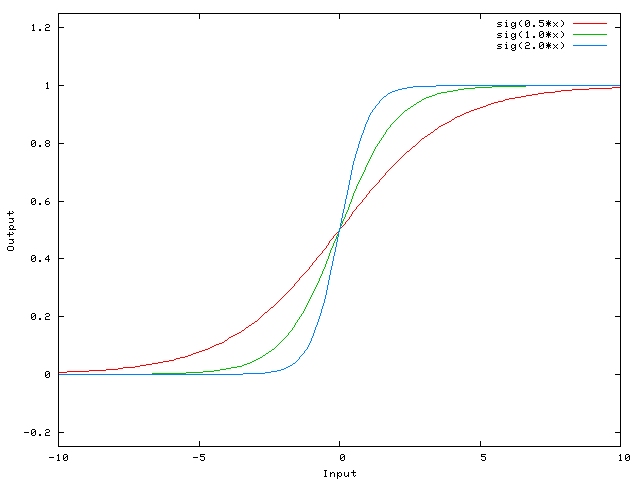
Меняя значение веса W0 мы изменяем наклон кривой, степень её крутизны, это удобно, но что если нам надо что бы исходящий сигнал был равен 0 когда X равен 2? Просто изменить наклон кривой не получится – не выйдет сместить всю кривую направо.
Это как раз то, что делает Биас. Если мы добавим Биас к нашей нейронной сети, например так:
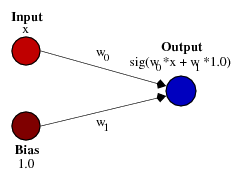
… тогда выходной сигнал нашей нейронной сети будет считаться sig(w0*x + w1*1.0). Соответственно так будет выглядеть наша функция при изменении веса W1:
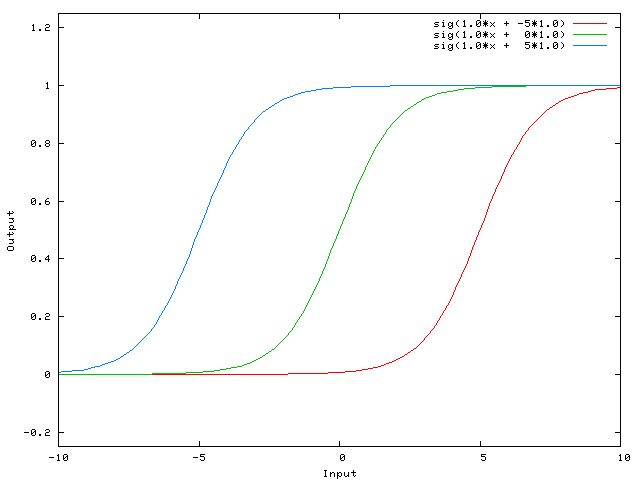
Вес W1 равный -5 сдвинет кривую направо, поэтому выходной сигнал нейронной сети будет равен 0 при X равном 2
Биас полезен почти всегда так как позволяет смещать функцию активации влево или вправо, что может быть крайне важно для успешного обучения.
Простой пример поможет понять. Представим простейшую нейронную сеть без скрытого слоя, только один входящий и 1 исходящий нейрон
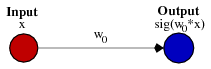
Выходной сигнал нейронной сети подсчитывается умножением веса W0 на сигнал X и применением активационной функции (чаще всего сигмоид) к произведению.
Пример функций, которых мы получим при разных значениях веса W0

Меняя значение веса W0 мы изменяем наклон кривой, степень её крутизны, это удобно, но что если нам надо что бы исходящий сигнал был равен 0 когда X равен 2? Просто изменить наклон кривой не получится – не выйдет сместить всю кривую направо.
Это как раз то, что делает Биас. Если мы добавим Биас к нашей нейронной сети, например так:

… тогда выходной сигнал нашей нейронной сети будет считаться sig(w0*x + w1*1.0). Соответственно так будет выглядеть наша функция при изменении веса W1:

Вес W1 равный -5 сдвинет кривую направо, поэтому выходной сигнал нейронной сети будет равен 0 при X равном 2
Вычисление исходящего сигнала нейронной сети
На данном этапе нам необходимо посчитать выходной сигнал нейронной сети используя веса инициализированные на предыдущем шаге.
def runAll(self, nn, X):
z=[0]
m = len(X)
a = [ copy.deepcopy(X) ] # a[0] is equal to the first input values
logFunc = self.logisticFunctionVectorize()
for i in range(1, len(nn['structure'])): # for each layer except the input
a[i-1] = np.c_[ np.ones(m), a[i-1]]; # add bias column to the previous matrix of activation functions
z.append(a[i-1]*nn['theta'][i].T) # for all neurons in current layer multiply corresponds neurons
# in previous layers by the appropriate weights and sum the productions
a.append(logFunc(z[i])) # apply activation function for each value
nn['z'] = z
nn['a'] = a
return a[len(nn['structure'])-1]
Более детальное описание переменных
Формат матрицы X: строки – вектора входящих значений (input values), столбцы – элементы векторов.
Z – лист с матрицами сумм произведений значений активационной функции из предыдущего слоя и весов соединяющих их с текущим слоем нейроном. Входящие значения не нуждаются в применении активационной функции, у них нет весов, поэтому мы пропускаем z[0] и начинаем с z[1]
a – лист с матрицами значения активационных функций
a[0] – матрица содержащая биас (единичный вектор размерностью m * 1) и входящие вектора X, то есть её размерность количество строк в X*(1+количество столбцов в X). Соответственно a[1] содержит матрицу значение активационных функций в первом скрытом слое, её размерность количество строк в X*(1+количество нейронов в первом скрытом слое)
Z – лист с матрицами сумм произведений значений активационной функции из предыдущего слоя и весов соединяющих их с текущим слоем нейроном. Входящие значения не нуждаются в применении активационной функции, у них нет весов, поэтому мы пропускаем z[0] и начинаем с z[1]
a – лист с матрицами значения активационных функций
a[0] – матрица содержащая биас (единичный вектор размерностью m * 1) и входящие вектора X, то есть её размерность количество строк в X*(1+количество столбцов в X). Соответственно a[1] содержит матрицу значение активационных функций в первом скрытом слое, её размерность количество строк в X*(1+количество нейронов в первом скрытом слое)
def logisticFunction(self, x):
a = 1/(1+np.exp(-x))
if a == 1: a = 0.99999 #make smallest step to the direction of zero
elif a == 0: a = 0.00001 # It is possible to use np.nextafter(0, 1) and
#make smallest step to the direction of one, but sometimes this step is too small and other algorithms fail :)
return a
def logisticFunctionVectorize(self):
return np.vectorize(self.logisticFunction)
Кратко говоря, с помощью команды np.vectorize функция теперь может принимать и считать матрицы значений. Например, для каждого элемента матрицы 10х1 будет посчитана логистическая функция, и возвращена матрица значений размерностью 10х1
Что это за условия в функции logisticFunction?
В коде выше обходится один важный подводный камень, связанный с округлением (тут придется забежать в перед). Предположим что вы готовите большую сеть, много слоев, много нейронов, вы инициализировали веса случайным образом и получается так, что сумма произведений на выходном слое для каждого нейрона очень маленькая, например -40. Логистическая функция от -40 радостно вернет вам единицу.
Далее нам будет нужно рассчитать ошибку нашей нейронной сети и мы передадим эту единицу для расчета логарифма от 1 — выходное значение [ log(1-output) ] естественно логарифм от единицы не определен, но ошибка не выскочит, просто наша нейронная сеть не будет тренироваться.
Далее нам будет нужно рассчитать ошибку нашей нейронной сети и мы передадим эту единицу для расчета логарифма от 1 — выходное значение [ log(1-output) ] естественно логарифм от единицы не определен, но ошибка не выскочит, просто наша нейронная сеть не будет тренироваться.
Из важного хочу заметить, что мы добавляем столбец биаса после того, как применили активационную функцию к сумме произведений. Это значит что биас всегда равен единице, а не логистической функции от единицы (что есть 0,73)
a[i-1] = np.c_[ np.ones(m), a[i-1]];
Кроме того, в финальной матрице активационных функций биас присутствует во всех слоях, кроме выходного слоя, в нём находятся только выходные сигналы нейронной сети (соответственно размерность матрицы = количество примеров*количество нейронов в выходном слое).
Для тех, кто не близко знаком с питоном отмечу, что в функцию runAll передаются не копии переменных (например сама нейронная сеть nn) а ссылки на них, поэтому когда мы изменяем переменную nn[‘z’] = z мы изменяем нашу сеть nn несмотря на то, что не передаем переменную nn обратно.
В результате данная функция (runAll) вернет нам матрицу выходных сигналов сети (её размерность количество выходных нейронов*1) и изменит матрицы z и a в переменной нейронной сети.
Ошибка нейронной сети
Ошибка выходного сигнала нейронной сети с регуляризацией считается по следующей формуле
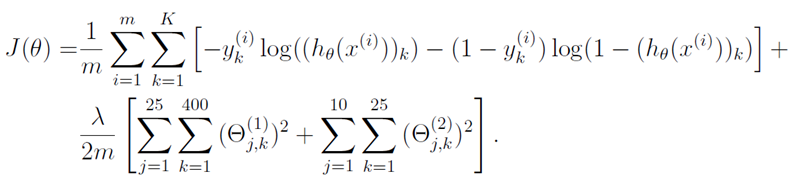
Картинка взята из материалов курса Machine Learning
m – количество примеров, K – количество выходных нейронов нейронной сети, h0(xi) – вектор выходных значений нейронной сети, ? — матрицы весов, где ?^1 матрица весов для первого скрытого слоя, lambda – коэффициент регуляризации.
Если она кажется вам довольно страшной и непонятной, это нормально :), в сущности, она раскладывается на 2 составные части, с которыми мы будем работать.
Подробное и понятное объяснение сути этой формулы растянется, и я не уверен, что оно нужно для такой подготовленной публики, поэтому пока опустим его, но пишите, при необходимости добавлю.
В чем суть регуляризации?
Вторая строчка формулы отвечает за регуляризацию, чем больше параметр регуляризации тем больше ошибка нейронной сети (так как во всей формуле происходит сумма двух положительных чисел), поэтому в процессе обучения, что бы снизить ошибку необходимо будет уменьшить веса нейронной сети, то есть высокий коэффициент регуляризации будет удерживать веса нейронной сети маленькими.
Собственно функция ошибки возвратит нам единственное значение в формате float, которое будет характеризовать насколько правильно наша нейронная сеть вычисляет выходной сигнал.
def costTotal(self, theta, nn, X, y, lamb):
m = len(X)
#following string is for fmin_cg computaton
if type(theta) == np.ndarray: nn['theta'] = self.roll(theta, nn['structure'])
y = np.matrix(copy.deepcopy(y))
hAll = self.runAll(nn, X) #feed forward to obtain output of neural network
cost = self.cost(hAll, y)
return cost/m+(lamb/(2*m))*self.regul(nn['theta']) #apply regularization
Функция возвращает ошибку нейронной сети для данной матрицы X входящих параметров.
Подсчитываем первую часть формулы, непосредственно ошибку сети
def cost(self, h, y):
logH=np.log(h)
log1H=np.log(1-h)
cost=-1*y.T*logH-(1-y.T)*log1H #transpose y for matrix multiplication
return cost.sum(axis=0).sum(axis=1) # sum matrix of costs for each output neuron and input vector
Считаем регуляризацию
def regul(self, theta):
reg=0
thetaLocal=copy.deepcopy(theta)
for i in range(1,len(thetaLocal)):
thetaLocal[i]=np.delete(thetaLocal[i],0,1) # delete bias connection
thetaLocal[i]=np.power(thetaLocal[i], 2) # square the values because they can be negative
reg+=thetaLocal[i].sum(axis=0).sum(axis=1) # sum at first rows, than columns
return reg
Допускаем цикл по массиву с матрицами theta так как предполагается что у нас весьма ограниченное количество слоев, производительности не будет нанесен большой урон.
Удаляем из регуляризации связь с биасом так как он вполне может принимать большое значение, если нам надо сильно сдвинуть логистическую функцию по оси Х.
Вычисление градиента
На этом этапе мы можем создать нейронную сеть, посчитать выходной сигнал и ошибку, теперь необходимо только вычислить градиент и реализовать алгоритм коррекции весов.
На этом шаге нам не обойтись без цикла по входящим векторам и для того, что бы немного ускорить расчет градиента, мы выносим максимум операций перед циклом. Например на предыдущих шагах мы специально спроектировали функцию runAll таким образом что бы она вычисляла матрицу входных значений, а не вектора (строки) поштучно, на этом этапе мы заранее рассчитаем выходные значения, затем будем обращаться к ним в цикле. По экспериментальным замерам данные фичи ускоряют функцию дополнительно на 25%
Мы используем обратный цикл по слоям нейронной сети от последнего к первому, так как нам надо вычислять ошибку и передавать её на слой назад, что бы вычислять следующую и т.д.
Основная сложность состоит в том, что бы не запутаться в индексах переменных. Например в большинстве документации по нейронным сетям для к примеру трехслойной сети (с одним скрытым слоем), дельта ошибки выходного слоя будет иметь индекс 3, понятно, что в этом случае лист должен состоять из четырех элементов, при этом лист градиентов состоит из 3 элементов.
def backpropagation(self, theta, nn, X, y, lamb):
layersNumb=len(nn['structure'])
thetaDelta = [0]*(layersNumb)
m=len(X)
#calculate matrix of outpit values for all input vectors X
hLoc = copy.deepcopy(self.runAll(nn, X))
yLoc=np.matrix(y)
thetaLoc = copy.deepcopy(nn['theta'])
derFunct=np.vectorize(lambda x: (1/(1+np.exp(-x)))*(1-(1/(1+np.exp(-x)))) )
zLoc = copy.deepcopy(nn['z'])
aLoc = copy.deepcopy(nn['a'])
for n in range(0, len(X)):
delta = [0]*(layersNumb+1) #fill list with zeros
delta[len(delta)-1]=(hLoc[n].T-yLoc[n].T) #calculate delta of error of output layer
for i in range(layersNumb-1, 0, -1):
if i>1: # we can not calculate delta[0] because we don't have theta[0] (and even we don't need it)
z = zLoc[i-1][n]
z = np.c_[ [[1]], z ] #add one for correct matrix multiplication
delta[i]=np.multiply(thetaLoc[i].T*delta[i+1],derFunct(z).T)
delta[i]=delta[i][1:]
thetaDelta[i] = thetaDelta[i] + delta[i+1]*aLoc[i-1][n]
for i in range(1, len(thetaDelta)):
thetaDelta[i]=thetaDelta[i]/m
thetaDelta[i][:,1:]=thetaDelta[i][:,1:]+thetaLoc[i][:,1:]*(lamb/m) #regularization
if type(theta) == np.ndarray: return np.asarray(self.unroll(thetaDelta)).reshape(-1) # to work also with fmin_cg
return thetaDelta
Функция возвращает лист элементы которого являются матрицами, размерности которых совпадают с размерностью матриц theta
При этом данная функция лямбда, это ни что иное как производная от активационной функции (сигмоида), поэтому если вы хотите заменить активационную функцию меняйте еще и производную
lambda x: (1/(1+np.exp(-x)))*(1-(1/(1+np.exp(-x))))
Тестирование
Теперь мы можем протестировать нашу нейронную сеть и даже попробовать её обучить чему нибудь :)
Для начала научим нашу сеть простой сегментации, все значения в пределах [0;5) это нуль, [5;9] это единица
nn=nt.create([1, 1000, 1])
lamb=0.3
cost=1
alf = 0.2
xTrain = [[0], [1], [1.9], [2], [3], [3.31], [4], [4.7], [5], [5.1], [6], [7], [8], [9]]
yTrain = [[0], [0], [0], [0], [0], [0], [0], [0], [1], [1], [1], [1], [1], [1]]
xTest= [[0.4], [1.51], [2.6], [3.23], [4.87], [5.78], [6.334], [7.667], [8.22], [9.1]]
yTest = [[0], [0], [0], [0], [0], [1], [1], [1], [1], [1]]
theta = nt.unroll(nn['theta'])
print(nt.runAll(nn, xTest))
theta = optimize.fmin_cg(nt.costTotal, fprime=nt.backpropagation,
x0=theta, args=(nn, xTrain, yTrain, lamb), maxiter=200)
print(nt.runAll(nn, xTest))
Результат. Вывод нейронной сети до тренировки, тренировка и после тренировки. Видно, что после тренировки первые пять значений ближе к нулю, вторые пять ближе к единице.

В предыдущем примере обучение контролировала функция fmin_cg теперь же мы будем менять theta(веса сети) самостоятельно.
Поставим простую задачу, отличать восходящую тенденцию от нисходящей. Нейронной сети на вход будут подаваться 4 числа, если они последовательно увеличиваются, это единица, если уменьшаются, это нуль.
nn=nt.create([4, 1000, 1])
lamb=0.3
cost=1
alf = 0.2
xTrain = [[1, 2.3, 4.5, 5.3], [1.1, 1.3, 2.4, 2.4], [1.9, 1.7, 1.5, 1.3], [2.3, 2.9, 3.3, 4.9], [3, 5.2, 6.1, 8.2], [3.31, 2.9, 2.4, 1.5], [4.9, 5.7, 6.1, 6.3],
[4.85, 5.0, 7.2, 8.1], [5.9, 5.3, 4.2, 3.3], [7.7, 5.4, 4.3, 3.9], [6.7, 5.3, 3.2, 1.4], [7.1, 8.6, 9.1, 9.9], [8.5, 7.4, 6.3, 4.1], [9.8, 5.3, 3.1, 2.9]]
yTrain = [[1], [1], [0], [1], [1], [0], [1],
[1], [0], [0], [0], [1], [0], [0]]
xTest= [[0.4, 1.9, 2.5, 3.1], [1.51, 2.0, 2.4, 3.8], [2.6, 5.1, 6.2, 7.2], [3.23, 4.1, 4.3, 4.9], [7.1, 7.6, 8.2, 9.3],
[5.78, 5.1, 4.5, 3.55], [6.33, 4.8, 3.4, 2.5], [7.67, 6.45, 5.8, 4.31], [8.22, 6.32, 5.87, 3.59], [9.1, 8.5, 7.7, 6.1]]
yTest = [[1], [1], [1], [1], [1],
[0], [0], [0], [0], [0]]
while cost>0:
cost=nt.costTotal(False, nn, xTrain, yTrain, lamb)
costTest=nt.costTotal(False, nn, xTest, yTest, lamb)
delta=nt.backpropagation(False, nn, xTrain, yTrain, lamb)
nn['theta']=[nn['theta'][i]-alf*delta[i] for i in range(0,len(nn['theta']))]
print('Train cost ', cost[0,0], 'Test cost ', costTest[0,0])
print(nt.runAll(nn, xTest))
Спустя 400 итераций (примерно 1 мин.) по каким то причинам у последнего тестового примера самая высокая ошибка (выход нейронной сети 0.13), скорее всего в этом случае для повышения качества помогло бы добавить тренировочные данные.

В цикле изменяем theta для того, что бы добиться максимального результата. Получается, что мы как бы скользим к локальному минимуму функции (а если бы мы добавляли градиент, то мы шли бы к локальному максимуму). Переменная alf часто называемая «скоростью обучения» отвечает за то как сильно мы будем изменять theta в каждой итерации. При этом если вы установите параметр альфа слишком большим, ошибка сети может даже увеличиваться или прыгать вверх и вниз так как функция будет просто перешагивать локальный минимум.
Как видно, вся нейронная сеть состоит из одной переменной типа dict, поэтому её легко серрилизовать, и сохранить в простом текстовом фале и так же восстановить для дальнейшего использования.
Возможно следующая публикация будет на тему как еще ускорить данный код (и любой другой, написанный на Python) с помощью вычислений на GPU
Полный листинг модуля, используйте по своему усмотрению
import copy
import numpy as np
import random as rd
import theano.tensor as th
class network:
# layers -list [5 10 10 5] - 5 input, 2 hidden
# layers (10 neurons each), 5 output
def create(self, layers):
theta = [0]
# for each layer from the first (skip zero layer!)
for i in range(1, len(layers)):
# create nxM+1 matrix (+bias!) with random floats in range [-1; 1]
theta.append(
np.mat(np.random.uniform(-1, 1, (layers[i], layers[i - 1] + 1))))
nn = {'theta': theta, 'structure': layers}
return nn
def runAll(self, nn, X):
z = [0]
m = len(X)
a = [copy.deepcopy(X)] # a[0] is equal to the first input values
logFunc = self.logisticFunctionVectorize()
# for each layer except the input
for i in range(1, len(nn['structure'])):
# add bias column to the previous matrix of activation functions
a[i - 1] = np.c_[np.ones(m), a[i - 1]]
# for all neurons in current layer multiply corresponds neurons
z.append(a[i - 1] * nn['theta'][i].T)
# in previous layers by the appropriate weights and sum the
# productions
a.append(logFunc(z[i])) # apply activation function for each value
nn['z'] = z
nn['a'] = a
return a[len(nn['structure']) - 1]
def run(self, nn, input):
z = [0]
a = []
a.append(copy.deepcopy(input))
a[0] = np.matrix(a[0]).T # nx1 vector
logFunc = self.logisticFunctionVectorize()
for i in range(1, len(nn['structure'])):
a[i - 1] = np.vstack(([1], a[i - 1]))
z.append(nn['theta'][i] * a[i - 1])
a.append(logFunc(z[i]))
nn['z'] = z
nn['a'] = a
return a[len(nn['structure']) - 1]
def logisticFunction(self, x):
a = 1 / (1 + np.exp(-x))
if a == 1:
a = 0.99999 # make smallest step to the direction of zero
elif a == 0:
a = 0.00001 # It is possible to use np.nextafter(0, 1) and
# make smallest step to the direction of one, but sometimes this step
# is too small and other algorithms fail :)
return a
def logisticFunctionVectorize(self):
return np.vectorize(self.logisticFunction)
def costTotal(self, theta, nn, X, y, lamb):
m = len(X)
# following string is for fmin_cg computaton
if type(theta) == np.ndarray:
nn['theta'] = self.roll(theta, nn['structure'])
y = np.matrix(copy.deepcopy(y))
# feed forward to obtain output of neural network
hAll = self.runAll(nn, X)
cost = self.cost(hAll, y)
# apply regularization
return cost / m + (lamb / (2 * m)) * self.regul(nn['theta'])
def cost(self, h, y):
logH = np.log(h)
log1H = np.log(1 - h)
# transpose y for matrix multiplication
cost = -1 * y.T * logH - (1 - y.T) * log1H
# sum matrix of costs for each output neuron and input vector
return cost.sum(axis=0).sum(axis=1)
def regul(self, theta):
reg = 0
thetaLocal = copy.deepcopy(theta)
for i in range(1, len(thetaLocal)):
# delete bias connection
thetaLocal[i] = np.delete(thetaLocal[i], 0, 1)
# square the values because they can be negative
thetaLocal[i] = np.power(thetaLocal[i], 2)
# sum at first rows, than columns
reg += thetaLocal[i].sum(axis=0).sum(axis=1)
return reg
def backpropagation(self, theta, nn, X, y, lamb):
layersNumb = len(nn['structure'])
thetaDelta = [0] * (layersNumb)
m = len(X)
# calculate matrix of outpit values for all input vectors X
hLoc = copy.deepcopy(self.runAll(nn, X))
yLoc = np.matrix(y)
thetaLoc = copy.deepcopy(nn['theta'])
derFunct = np.vectorize(
lambda x: (1 / (1 + np.exp(-x))) * (1 - (1 / (1 + np.exp(-x)))))
zLoc = copy.deepcopy(nn['z'])
aLoc = copy.deepcopy(nn['a'])
for n in range(0, len(X)):
delta = [0] * (layersNumb + 1) # fill list with zeros
# calculate delta of error of output layer
delta[len(delta) - 1] = (hLoc[n].T - yLoc[n].T)
for i in range(layersNumb - 1, 0, -1):
# we can not calculate delta[0] because we don't have theta[0]
# (and even we don't need it)
if i > 1:
z = zLoc[i - 1][n]
# add one for correct matrix multiplication
z = np.c_[[[1]], z]
delta[i] = np.multiply(
thetaLoc[i].T * delta[i + 1], derFunct(z).T)
delta[i] = delta[i][1:]
thetaDelta[i] = thetaDelta[i] + delta[i + 1] * aLoc[i - 1][n]
for i in range(1, len(thetaDelta)):
thetaDelta[i] = thetaDelta[i] / m
thetaDelta[i][:, 1:] = thetaDelta[i][:, 1:] + thetaLoc[i][:, 1:] * (lamb / m) # regularization
if type(theta) == np.ndarray:
# to work also with fmin_cg
return np.asarray(self.unroll(thetaDelta)).reshape(-1)
return thetaDelta
# create 1d array form lists like theta
def unroll(self, arr):
for i in range(0, len(arr)):
arr[i] = np.matrix(arr[i])
if i == 0:
res = (arr[i]).ravel().T
else:
res = np.vstack((res, (arr[i]).ravel().T))
res.shape = (1, len(res))
return res
# roll back 1d array to list with matrices according to given structure
def roll(self, arr, structure):
rolled = [arr[0]]
shift = 1
for i in range(1, len(structure)):
temparr = copy.deepcopy(
arr[shift:shift + structure[i] * (structure[i - 1] + 1)])
temparr.shape = (structure[i], structure[i - 1] + 1)
rolled.append(np.matrix(temparr))
shift += structure[i] * (structure[i - 1] + 1)
return rolled
UPD
Спасибо всем, кто плюсует.


ilvar
Будет отлично, если вы приведете код к PEP-8, это умеет делать PyCharm, также есть отдельные тулзы.
По теме — меня в свое время этот курс Ына приятно поразил, я понял, что ML вообще и нейронные сети в частности — чистая математика, безо всякой квантово-тороидальной (/sarcasm) магии.
Arristotel Автор
Не минусуйте, PEP-8 это хорошо
Да, те, кто работает с нейронными сетями делятся на 2 лагеря: для одних нейронная сеть предсказывает выходные значения, а для других вычисляет :)