
Индекс на основе Z-order кривой в сравнении с R-деревом имеет массу преимуществ, он:
- реализован как обычное B-дерево, а мы знаем что
- страницы B-дерева имеют лучшую заполняемость, кроме того,
- Z-ключи сами по себе более компактны
- B-дерево имеет естественный порядок обхода, в отличие от R-дерева
- B-дерево быстрее строится
- B-дерево лучше сбалансировано
- B-дерево понятнее, не зависит от эвристики расщепления/слияния страниц
- B-дерево не деградирует при постоянных изменениях
- ...
Впрочем, у индексов на основе Z-order есть и недостаток — сравнительно низкая производительность :). Под катом мы попробуем разобраться с чем связан этот недостаток и можно ли что-то с этим сделать.
Грубо, смысл Z-кривой таков — мы чередуем разряды x & y координат в одном значении, в результате. Пример — (x = 33 (010 0001), y=22 (01 0110), Z=1577 (0110 0010 1001). Если у двух точек близкие координаты, то скорее всего и Z- значения у них будут близки.
Трехмерный (или более) вариант устроен так же, мы чередуем разряды трех (или более) координат.
А для поиска в некотором экстенте мы должны “растеризовать” все значения Z-кривой для этого экстента, найти непрерывные интервалы и в каждом осуществить поиск.
Вот иллюстрация для экстента [111000...111000][111400...111400] (675 интервалов), правый верхний угол (каждая непрерывная ломаная — один интервал):
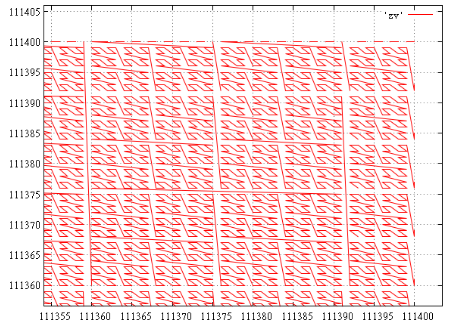
А, например, для экстента [111000...111000][112000...112000] мы получаем 1688 непрерывных интервалов, очевидно, их число в основном зависит от длины периметра. Забегая вперед, на тестовых данных в этот экстент попало 15 точек в 6 интервалах.
Да, большая часть этих интервалов мала, вплоть до вырожденного — из одного значения. И тем не менее, даже если во всём этом экстенте всего одно значение, оно может быть в любом из интервалов. И, нравится нам это или нет, придется делать все 1688 подзапросов чтобы узнать сколько там точек в действительности.
Просмотреть всё от значения левого нижнего угла до правого верхнего — не вариант, разница между углами в данном случае — 3 144 768, нам придется просмотреть в три с лишним раза больше данных, и это далеко не самый худший случай. Например, экстент [499500...499500][500500...500500] даст диапазон в 135 263 808 значений, в ~135 раз больше площади экстента.
И тут мы можем задать традиционный вопрос —
А что, если ...
Предположим, у нас вообще пустой индекс, неужели, надо делать все эти сотни и тысячи подзапросов, чтобы понять это? Нет, достаточно одного — от левого нижнего до правого верхнего угла.
Теперь предположим, что экстент достаточно мал, а данные разрежены и шансов найти что-то мало. Выполним тот же запрос от угла до угла. Если ничего не нашлось, значит ничего и нет. В противном случае есть шанс. Но как мы видели, площадь заметаемая запросом от угла до угла может многократно превышать поисковый экстент и у нас нет никакого желания вычитывать заведомо ненужные данные. Поэтому мы не будем просматривать весь курсор, а возьмем из него лишь минимальное Z-значение. Для этого запрос выполняется с (order by) и (top 1).
Итак, у нас есть некоторое значение. Допустим, это значение не из нашего экстента, что это может дать? Самое время вспомнить, что у нас есть сортированный массив [1...N] диапазонов подзапросов. Мы выполним двоичный поиск и узнаем, между какими подзапросами втиснулось это значение, пусть, между m и m+1. Замечательно, значит запросы от 1 до m можно не выполнять, там заведомо ничего нет.
Если значение принадлежит нашему экстенту, значит оно попадает в один из наших диапазонов и мы также можем найти в какой, пусть тоже m. Как и раньше, запросы с номерами 1 … m-1 можно не выполнять. А вот интервал с номером m заслуживает отдельного запроса, который выдаст нам всё, что в нем расположено.
Что же, возможно, еще остались данные, продолжим. Опять выполним запрос, но уже не от угла до угла, а от начала интервала m+1 до правого верхнего угла. И будем так поступать, пока не дойдем до конца списка интервалов.
Вот и вся идея, заметим, она отлично работает и в случае, когда в экстент попадает много или даже очень много данных. На первый взгляд, это позволит радикально снизить число запросов и ускорить работу.
Самое время проверить идею на практике. В качестве тестовой площадки станем использовать PostgeSQL 9.6.1, GiST. Замеры проводились на скромной виртуальной машине с двумя ядрами и 4 Гб ОЗУ, поэтому времена не имеют абсолютной ценности, а вот числам прочитанных страниц можно доверять.
Исходные данные
В качестве данных использованы 100 млн случайных точек в экстенте [0...1 000 000][0...1 000 000].
Заведем таблицу для 2-мерных точечных данных:
create table test_points (x integer,y integer);Данные создадим:
for (i = 0; i < 100000000; i++)
{
x = int(1000000 * rand());
y = int(1000000 * rand());
print x"\t«z;
}
exit(0);
}
Отсортируем полученный файл (объяснение далее) и оператором COPY зальем его в таблицу:
COPY test_points from '/home/.../data.csv';Заливка таблицы занимает несколько минут. Размер данных (\dt+) — 4358 Mb
R-tree
Соответствующий индекс создается командой:
create index test_gist_idx on test_points using gist ((point(x,y)));Но есть нюанс. На случайных данных индекс строится очень долго (во всяком случае у автора он не успел построиться за ночь). Построение на заранее отсортированных данных заняло около часа.
Размер индекса (\di+) — 9031 Mb
В сущности, для нас порядок данных в таблице не важен, но он должен быть общим для разных методов, поэтому пришлось использовать отсортированную таблицу.
Тестовый запрос выглядит так:
select count(1) from test_points where
point(x,y) <@ box(point("xmin","ymin"),point("xmax","ymax"));
Проверка на обычных индексах
Для проверки работоспособности будем выполнять пространственные запросы и на отдельных индексах по x & y. Изготавливаются они так:
create index x_test_points on test_points (x);
create index y_test_points on test_points (y);
Занимает это несколько минут.
Тестовый запрос:
select count(1) from test_points where
x >= "xmin" and x <= "xmax" and y >= "ymin" and y <= "ymax";
Z-индекс
Теперь нам потребуется функция, умеющая преобразовывать x,y координаты в Z-значение.
Для начала создадим расширение, в нём функцию:
CREATE FUNCTION zcurve_val_from_xy(bigint, bigint) RETURNS bigint
AS 'MODULE_PATHNAME'
LANGUAGE C IMMUTABLE STRICT;
static uint32 stoBits[8] = {0x0001, 0x0002, 0x0004, 0x0008,
0x0010, 0x0020, 0x0040, 0x0080};
uint64
zcurve_fromXY (uint32 ix, uint32 iy)
{
uint64 val = 0;
int curmask = 0xf;
unsigned char *ptr = (unsigned char *)&val;
int i;
for (i = 0; i < 8; i++)
{
int xp = (ix & curmask) >> (i<<2);
int yp = (iy & curmask) >> (i<<2);
int tmp = (xp & stoBits[0]) | ((yp & stoBits[0])<<1) |
((xp & stoBits[1])<<1) | ((yp & stoBits[1])<<2) |
((xp & stoBits[2])<<2) | ((yp & stoBits[2])<<3) |
((xp & stoBits[3])<<3) | ((yp & stoBits[3])<<4);
curmask <<= 4;
ptr[i] = (unsigned char)tmp;
}
return val;
}
Datum
zcurve_val_from_xy(PG_FUNCTION_ARGS)
{
uint64 v1 = PG_GETARG_INT64(0);
uint64 v2 = PG_GETARG_INT64(1);
PG_RETURN_INT64(zcurve_fromXY(v1, v2));
}
Теперь (после CREATE EXTENSION, конечно) Z-индекс строится следующим образом:
create index zcurve_test_points on test_points(zcurve_val_from_xy(x, y));Это занимает несколько минут (и не требует сортировки данных).
Размер индекса (\di+) — 2142 Mb (в ~4 раза меньше чем у R-tree)
Поиск в Z-индексе
Итак, в нашем первом (назовем его “наивным”) варианте мы будем поступать так:
- Для экстента размером dx*dy заводим массив идентификаторов соответствующего размера
- Для каждой точки в экстенте вычисляес Z-значение
- Сортируем массив идентификаторов
- Находим непрерывные интервалы
- Для каждого интервала выполняем подзапрос вида:
select * from test_points where zcurve_val_from_xy(x, y) between $1 and $2
- Получаем результат
Для поиска с помощью этого варианта будем использовать функцию (тело ниже):
CREATE FUNCTION zcurve_oids_by_extent(bigint, bigint, bigint, bigint)
RETURNS bigint
AS 'MODULE_PATHNAME'
LANGUAGE C IMMUTABLE STRICT;
Пространственный запрос с использованием этой функции выглядит так:
select zcurve_oids_by_extent("xmin","ymin","xmax","ymax") as count;Функция возвращает только число попаданий, сами данные при необходимости могут быть выведены с помощью “elog(INFO…)”.
Второй, улучшенный, (назовём его “с пробами”) вариант выглядит следующим образом:
- для экстента размером dx*dy заводим массив идентификаторов соответствующего размера
- для каждой точки в экстенте вычисляес Z-значение
- сортируем массив идентификаторов
- находим непрерывные интервалы
- стартуем с первого найденного интервала:
- Выполняем “пробный” запрос типа (параметры — границы интервала):
select * from test_points where zcurve_val_from_xy(x, y) between $1 and $2 order by zcurve_val_from_xy(x, y) limit 1
- Этот запрос выдает нам строку таблицы с наименьшим Z-значением от начала текущего тестируемого интервала до конца поискового экстента.
- Если запрос ничего не нашел, значит и данных в поисковом экстенте не осталось, выходим.
- Теперь мы можем проанализировать найденное Z-значение:
- Смотрим, попало ли оно в какой — либо из наших интервалов.
- Если нет, находим номер следующего оставшегося интервала и переходим на пункт 5.
- Если попало, выполняем запрос для этого интервала типа:
select * from test_points where zcurve_val_from_xy(x, y) between $1 and $2
- Берем следующий интервал и переходим на пункт 5.
- Выполняем “пробный” запрос типа (параметры — границы интервала):
Для поиска с помощью этого варианта будем использовать функцию:
CREATE FUNCTION zcurve_oids_by_extent_ii(bigint, bigint, bigint, bigint)
RETURNS bigint
AS 'MODULE_PATHNAME'
LANGUAGE C IMMUTABLE STRICT;
Пространственный запрос с использованием этой функции выглядит так:
select zcurve_oids_by_extent_ii("xmin","ymin","xmax","ymax") as count;Функция также возвращает только число попаданий.
Растеризация
В описанных алгоритмах использован весьма простой и неэффективный алгоритм “растеризации” — получения списка интервалов.
С другой стороны, нетрудно выполнить замеры средних времен его работы на случайных экстентах нужного размера. Вот они:
| Экстент dx * dy | Ожидаемое среднее число точек в выдаче | Время, мсек |
|---|---|---|
| 100X100 | 1 | .96 (.37 + .59) |
| 316X316 | 10 | 11 (3.9 + 7.1) |
| 1000X1000 | 100 | 119.7 (35 + 84.7) |
| 3162X3162 | 1000 | 1298 (388 + 910) |
| 10000X10000 | 10 000 | 14696 (3883 + 10813) |
Результаты
Вот сводная таблица с данными.
| Npoints | Type | Time(ms) | Reads | Shared Hits |
|---|---|---|---|---|
| 1 | X&Y rtree Z-value Z-value-ii |
43.6 .5 8.3(9.4) 1.1(2.2) |
59.0173 4.2314 4.0988 4.1984 (12.623) |
6.1596 2.6565 803.171 20.1893 (57.775) |
| 10 | X&Y rtree Z-value Z-value-ii |
83.5 .6 15(26) 4(15) |
182.592 13.7341 14.834 14.832 (31.439) |
9.24363 2.72466 2527.56 61.814 (186.314) |
| 100 | X&Y rtree Z-value Z-value-ii |
220 2.1 80(200) 10(130) |
704.208 95.8179 95.215 96.198 (160.443) |
16.528 5.3754 8007.3 208.214 (600.049) |
| 1000 | X&Y rtree Z-value Z-value-ii |
740 12 500(1800) 200(1500) |
3176.06 746.617 739.32 739.58 (912.631) |
55.135 25.439 25816 842.88 (2028.81) |
| 10 000 | X&Y rtree Z-value Z-value-ii |
2 500 70 … 1 200 4700(19000) 1300(16000) |
12393.2 4385.64 4284.45 4305.78 (4669) |
101.43 121.56 86274.9 5785.06 (9188) |
Type -
- ‘X&Y’ — использование отдельных индексов по x & y
- ‘rtree’ — запрос через R-tree
- Z-value — честный поиск через интервалы
- ‘Z-value-ii’ — поиск через интервалы с пробами
Time(ms) — среднее время выполнения запроса. В данных условиях величина весьма нестабильная, зависит и от кэша СУБД и от дискового кэша виртуальной машины и от дискового кэша хост-системы. Здесь приведена скорее для справки. Для Z-value и Z-value-ii приведены 2 числа. В скобках — фактическое время. Без скобок — время за вычетом затрат на “растеризацию”.
Reads — среднее число чтений на запрос (получено через EXPLAIN (ANALYZE,BUFFERS))
Shared hits — число обращений к буферам (...)
Для Z-value-ii в колонках Reads & Shared hits приведены 2 числа. В скобках — полное число чтений. Без скобок — за вычетом зондирующих запросов с order by и limit 1. Сделано это из за мнения, что такой запрос вычитывает все данные в интервале, сортирует и отдает минимальное, вместо того, чтобы просто отдать 1 значение из уже отсортированного индекса. Поэтому статистика по таким запросам была сочтена излишней, но приведена для справки.
Времена показаны на вторых прогонах, на разогретом сервере и виртуальной машине. Количества прочитанных буферов — на свеже-поднятом сервере.
Во всех типах запросов читались и данные самой таблицы не принадлежащие индексам. Впрочем, это одни и те же данные одной и той же таблицы, так что для всех типов запросов мы получили константные величины.
Выводы
- R-дерево всё же очень хорошо в статике, КПД чтений страниц весьма высок.
- А вот Z-order индексу иногда приходится читать страницы, на которых нет нужных данных. Это происходит, когда тестирующий курсор попадает между интервалов, есть вероятность, что в этом промежутке окажется много чужих точек и конкретная страница не содержит никаких итоговых данных.
- И тем не менее, за счет более плотной упаковки Z-order близок к R-дереву по числу реально прочитанных страниц. Это говорит о том, что потенциально Z-order способен выдавать близкую производительность.
- Z-order индекс читает огромное количество страниц из кэша т.к. многократно делаются запросы по одному и тому же месту. С другой стороны, эти чтения стоят относительно недорого.
- На больших запросах Z-order сильно проигрывает в скорости R-дереву. Объясняется это тем, что для выполнения подзапросов мы пользуемся SPI — высокоуровневым и не слишком быстрым механизмом. И с “растеризацией”, конечно, надо что-то делать.
- На первый взгляд, использование проб интервалов не сильно то и ускорило работу, а формально даже ухудшило статистику чтений страниц. Но надо понимать, что это издержки высокоуровневых средств, которыми пришлось воспользоваться. Потенциально индекс на основе Z-order не хуже R-дерева по производительности и сильно лучше по остальным тактико-техническим характеристикам.
Перспективы
Для создания на основе Z-order кривой полноценного пространственного индекса, который был бы способен на равных соревноваться с R-деревом, необходимо решить следующие проблемы:
- придумать недорогой алгоритм получения списка подинтервалов по экстенту
- перейти на низкоуровневый доступ к дереву индекса
К счастью, и то и другое не выглядит чем-то невозможным.
#include "postgres.h"
#include "catalog/pg_type.h"
#include "fmgr.h"
#include <string.h>
#include "executor/spi.h"
PG_MODULE_MAGIC;
uint64 zcurve_fromXY (uint32 ix, uint32 iy);
void zcurve_toXY (uint64 al, uint32 *px, uint32 *py);
static uint32 stoBits[8] = {0x0001, 0x0002, 0x0004, 0x0008,
0x0010, 0x0020, 0x0040, 0x0080};
uint64
zcurve_fromXY (uint32 ix, uint32 iy)
{
uint64 val = 0;
int curmask = 0xf;
unsigned char *ptr = (unsigned char *)&val;
int i;
for (i = 0; i < 8; i++)
{
int xp = (ix & curmask) >> (i<<2);
int yp = (iy & curmask) >> (i<<2);
int tmp = (xp & stoBits[0]) | ((yp & stoBits[0])<<1) |
((xp & stoBits[1])<<1) | ((yp & stoBits[1])<<2) |
((xp & stoBits[2])<<2) | ((yp & stoBits[2])<<3) |
((xp & stoBits[3])<<3) | ((yp & stoBits[3])<<4);
curmask <<= 4;
ptr[i] = (unsigned char)tmp;
}
return val;
}
void
zcurve_toXY (uint64 al, uint32 *px, uint32 *py)
{
unsigned char *ptr = (unsigned char *)&al;
int ix = 0;
int iy = 0;
int i;
if (!px || !py)
return;
for (i = 0; i < 8; i++)
{
int tmp = ptr[i];
int tmpx = (tmp & stoBits[0]) + ((tmp & stoBits[2])>>1) + ((tmp & stoBits[4])>>2) + ((tmp & stoBits[6])>>3);
int tmpy = ((tmp & stoBits[1])>>1) + ((tmp & stoBits[3])>>2) + ((tmp & stoBits[5])>>3) + ((tmp & stoBits[7])>>4);
ix |= tmpx << (i << 2);
iy |= tmpy << (i << 2);
}
*px = ix;
*py = iy;
}
PG_FUNCTION_INFO_V1(zcurve_val_from_xy);
Datum
zcurve_val_from_xy(PG_FUNCTION_ARGS)
{
uint64 v1 = PG_GETARG_INT64(0);
uint64 v2 = PG_GETARG_INT64(1);
PG_RETURN_INT64(zcurve_fromXY(v1, v2));
}
static const int s_maxx = 1000000;
static const int s_maxy = 1000000;
#ifndef MIN
#define MIN(a,b) ((a)<(b)?(a):(b))
#endif
static int compare_uint64( const void *arg1, const void *arg2 )
{
const uint64 *a = (const uint64 *)arg1;
const uint64 *b = (const uint64 *)arg2;
if (*a == *b)
return 0;
return *a > *b ? 1: -1;
}
SPIPlanPtr prep_interval_request();
int fin_interval_request(SPIPlanPtr pplan);
int run_interval_request(SPIPlanPtr pplan, uint64 v0, uint64 v1);
SPIPlanPtr prep_interval_request()
{
SPIPlanPtr pplan;
char sql[8192];
int nkeys = 2;
Oid argtypes[2] = {INT8OID, INT8OID}; /* key types to prepare execution plan */
int ret =0;
if ((ret = SPI_connect()) < 0)
/* internal error */
elog(ERROR, "check_primary_key: SPI_connect returned %d", ret);
snprintf(sql, sizeof(sql), "select * from test_points where zcurve_val_from_xy(x, y) between $1 and $2");
/* Prepare plan for query */
pplan = SPI_prepare(sql, nkeys, argtypes);
if (pplan == NULL)
/* internal error */
elog(ERROR, "check_primary_key: SPI_prepare returned %d", SPI_result);
return pplan;
}
int fin_interval_request(SPIPlanPtr pplan)
{
SPI_finish();
return 0;
}
int
run_interval_request(SPIPlanPtr pplan, uint64 v0, uint64 v1)
{
Datum values[2]; /* key types to prepare execution plan */
Portal portal;
int cnt = 0, i;
values[0] = Int64GetDatum(v0);
values[1] = Int64GetDatum(v1);
portal = SPI_cursor_open(NULL, pplan, values, NULL, true);
if (NULL == portal)
/* internal error */
elog(ERROR, "check_primary_key: SPI_cursor_open");
for (;;)
{
SPI_cursor_fetch(portal, true, 8);
if (0 == SPI_processed || NULL == SPI_tuptable)
break;
{
TupleDesc tupdesc = SPI_tuptable->tupdesc;
for (i = 0; i < SPI_processed; i++)
{
HeapTuple tuple = SPI_tuptable->vals[i];
//elog(INFO, "%s, %s", SPI_getvalue(tuple, tupdesc, 1), SPI_getvalue(tuple, tupdesc, 2));
cnt++;
}
}
}
SPI_cursor_close(portal);
return cnt;
}
PG_FUNCTION_INFO_V1(zcurve_oids_by_extent);
Datum
zcurve_oids_by_extent(PG_FUNCTION_ARGS)
{
SPIPlanPtr pplan;
uint64 x0 = PG_GETARG_INT64(0);
uint64 y0 = PG_GETARG_INT64(1);
uint64 x1 = PG_GETARG_INT64(2);
uint64 y1 = PG_GETARG_INT64(3);
uint64 *ids = NULL;
int cnt = 0;
int sz = 0, ix, iy;
x0 = MIN(x0, s_maxx);
y0 = MIN(y0, s_maxy);
x1 = MIN(x1, s_maxx);
y1 = MIN(y1, s_maxy);
if (x0 > x1)
elog(ERROR, "xmin > xmax");
if (y0 > y1)
elog(ERROR, "ymin > ymax");
sz = (x1 - x0 + 1) * (y1 - y0 + 1);
ids = (uint64*)palloc(sz * sizeof(uint64));
if (NULL == ids)
/* internal error */
elog(ERROR, "cant alloc %d bytes in zcurve_oids_by_extent", sz);
for (ix = x0; ix <= x1; ix++)
for (iy = y0; iy <= y1; iy++)
{
ids[cnt++] = zcurve_fromXY(ix, iy);
}
qsort (ids, sz, sizeof(*ids), compare_uint64);
cnt = 0;
pplan = prep_interval_request();
{
// FILE *fl = fopen("/tmp/ttt.sql", "w");
int cur_start = 0;
int ix;
for (ix = cur_start + 1; ix < sz; ix++)
{
if (ids[ix] != ids[ix - 1] + 1)
{
cnt += run_interval_request(pplan, ids[cur_start], ids[ix - 1]);
// fprintf(fl, "EXPLAIN (ANALYZE,BUFFERS) select * from test_points where zcurve_val_from_xy(x, y) between %ld and %ld;\n", ids[cur_start], ids[ix - 1]);
// elog(INFO, "%d -> %d (%ld -> %ld)", cur_start, ix - 1, ids[cur_start], ids[ix - 1]);
// cnt++;
cur_start = ix;
}
}
if (cur_start != ix)
{
cnt += run_interval_request(pplan, ids[cur_start], ids[ix - 1]);
// fprintf(fl, "EXPLAIN (ANALYZE,BUFFERS) select * from test_points where zcurve_val_from_xy(x, y) between %ld and %ld;\n", ids[cur_start], ids[ix - 1]);
// elog(INFO, "%d -> %d (%ld -> %ld)", cur_start, ix - 1, ids[cur_start], ids[ix - 1]);
}
// fclose(fl);
}
fin_interval_request(pplan);
pfree(ids);
PG_RETURN_INT64(cnt);
}
//------------------------------------------------------------------------------------------------
struct interval_ctx_s {
SPIPlanPtr cr_;
SPIPlanPtr probe_cr_;
uint64 cur_val_;
uint64 top_val_;
FILE * fl_;
};
typedef struct interval_ctx_s interval_ctx_t;
int prep_interval_request_ii(interval_ctx_t *ctx);
int run_interval_request_ii(interval_ctx_t *ctx, uint64 v0, uint64 v1);
int probe_interval_request_ii(interval_ctx_t *ctx, uint64 v0);
int fin_interval_request_ii(interval_ctx_t *ctx);
int prep_interval_request_ii(interval_ctx_t *ctx)
{
char sql[8192];
int nkeys = 2;
Oid argtypes[2] = {INT8OID, INT8OID}; /* key types to prepare execution plan */
int ret =0;
if ((ret = SPI_connect()) < 0)
/* internal error */
elog(ERROR, "check_primary_key: SPI_connect returned %d", ret);
snprintf(sql, sizeof(sql), "select * from test_points where zcurve_val_from_xy(x, y) between $1 and $2");
ctx->cr_ = SPI_prepare(sql, nkeys, argtypes);
if (ctx->cr_ == NULL)
/* internal error */
elog(ERROR, "check_primary_key: SPI_prepare returned %d", SPI_result);
snprintf(sql, sizeof(sql), "select * from test_points where zcurve_val_from_xy(x, y) between $1 and %ld order by zcurve_val_from_xy(x::int4, y::int4) limit 1", ctx->top_val_);
ctx->probe_cr_ = SPI_prepare(sql, 1, argtypes);
if (ctx->probe_cr_ == NULL)
/* internal error */
elog(ERROR, "check_primary_key: SPI_prepare returned %d", SPI_result);
return 1;
}
int
probe_interval_request_ii(interval_ctx_t *ctx, uint64 v0)
{
Datum values[1]; /* key types to prepare execution plan */
Portal portal;
values[0] = Int64GetDatum(v0);
{
// uint32 lx, ly;
// zcurve_toXY (v0, &lx, &ly);
//
// elog(INFO, "probe(%ld:%d,%d)", v0, lx, ly);
}
if (ctx->fl_)
fprintf(ctx->fl_, "EXPLAIN (ANALYZE,BUFFERS) select * from test_points where zcurve_val_from_xy(x, y) between %ld and %ld order by zcurve_val_from_xy(x::int4, y::int4) limit 1;\n", v0, ctx->top_val_);
portal = SPI_cursor_open(NULL, ctx->probe_cr_, values, NULL, true);
if (NULL == portal)
/* internal error */
elog(ERROR, "check_primary_key: SPI_cursor_open");
{
SPI_cursor_fetch(portal, true, 1);
if (0 != SPI_processed && NULL != SPI_tuptable)
{
TupleDesc tupdesc = SPI_tuptable->tupdesc;
bool isnull;
HeapTuple tuple = SPI_tuptable->vals[0];
Datum dx, dy;
uint64 zv = 0;
dx = SPI_getbinval(tuple, tupdesc, 1, &isnull);
dy = SPI_getbinval(tuple, tupdesc, 2, &isnull);
zv = zcurve_fromXY(DatumGetInt64(dx), DatumGetInt64(dy));
// elog(INFO, "%ld %ld -> %ld", DatumGetInt64(dx), DatumGetInt64(dy), zv);
ctx->cur_val_ = zv;
SPI_cursor_close(portal);
return 1;
}
SPI_cursor_close(portal);
}
return 0;
}
int
run_interval_request_ii(interval_ctx_t *ctx, uint64 v0, uint64 v1)
{
Datum values[2]; /* key types to prepare execution plan */
Portal portal;
int cnt = 0, i;
values[0] = Int64GetDatum(v0);
values[1] = Int64GetDatum(v1);
// elog(INFO, "[%ld %ld]", v0, v1);
if (ctx->fl_)
fprintf(ctx->fl_, "EXPLAIN (ANALYZE,BUFFERS) select * from test_points where zcurve_val_from_xy(x, y) between %ld and %ld;\n", v0, v1);
portal = SPI_cursor_open(NULL, ctx->cr_, values, NULL, true);
if (NULL == portal)
/* internal error */
elog(ERROR, "check_primary_key: SPI_cursor_open");
for (;;)
{
SPI_cursor_fetch(portal, true, 8);
if (0 == SPI_processed || NULL == SPI_tuptable)
break;
{
TupleDesc tupdesc = SPI_tuptable->tupdesc;
for (i = 0; i < SPI_processed; i++)
{
HeapTuple tuple = SPI_tuptable->vals[i];
// elog(INFO, "%s, %s", SPI_getvalue(tuple, tupdesc, 1), SPI_getvalue(tuple, tupdesc, 2));
cnt++;
}
}
}
SPI_cursor_close(portal);
return cnt;
}
PG_FUNCTION_INFO_V1(zcurve_oids_by_extent_ii);
Datum
zcurve_oids_by_extent_ii(PG_FUNCTION_ARGS)
{
uint64 x0 = PG_GETARG_INT64(0);
uint64 y0 = PG_GETARG_INT64(1);
uint64 x1 = PG_GETARG_INT64(2);
uint64 y1 = PG_GETARG_INT64(3);
uint64 *ids = NULL;
int cnt = 0;
int sz = 0, ix, iy;
interval_ctx_t ctx;
x0 = MIN(x0, s_maxx);
y0 = MIN(y0, s_maxy);
x1 = MIN(x1, s_maxx);
y1 = MIN(y1, s_maxy);
if (x0 > x1)
elog(ERROR, "xmin > xmax");
if (y0 > y1)
elog(ERROR, "ymin > ymax");
sz = (x1 - x0 + 1) * (y1 - y0 + 1);
ids = (uint64*)palloc(sz * sizeof(uint64));
if (NULL == ids)
/* internal error */
elog(ERROR, "can't alloc %d bytes in zcurve_oids_by_extent_ii", sz);
for (ix = x0; ix <= x1; ix++)
for (iy = y0; iy <= y1; iy++)
{
ids[cnt++] = zcurve_fromXY(ix, iy);
}
qsort (ids, sz, sizeof(*ids), compare_uint64);
ctx.top_val_ = ids[sz - 1];
ctx.cur_val_ = 0;
ctx.cr_ = NULL;
ctx.probe_cr_ = NULL;
ctx.fl_ = NULL;//fopen("/tmp/ttt.sql", "w");
cnt = 0;
prep_interval_request_ii(&ctx);
{
int cur_start = 0;
int ix;
for (ix = cur_start + 1; ix < sz; ix++)
{
if (0 == probe_interval_request_ii(&ctx, ids[cur_start]))
break;
for (; cur_start < sz && ids[cur_start] < ctx.cur_val_; cur_start++);
// if (ctx.cur_val_ != ids[cur_start])
// {
// cur_start++;
// continue;
// }
ix = cur_start + 1;
if (ix >= sz)
break;
for (; ix < sz && ids[ix] == ids[ix - 1] + 1; ix++);
//elog(INFO, "%d %d %d", ix, cur_start, sz);
cnt += run_interval_request_ii(&ctx, ids[cur_start], ids[ix - 1]);
cur_start = ix;
}
}
if (ctx.fl_)
fclose(ctx.fl_);
fin_interval_request(NULL);
pfree(ids);
PG_RETURN_INT64(cnt);
}
Выкладываю здесь, а не выложены на github т.к. код сугубо экспериментальный и не имеет практической ценности.
PPS: Огромное спасибо ребятам из PostgresPro за то что сподвигли меня на эту работу.
Комментарии (7)

kashey
10.01.2017 12:47+2Очень хорошо, но есть пара проблем:
1. Z-code это, фактически linear quad-tree. Не R. И совсем не B. Все, что вы обьявили бонусами в начале статьи — не работает. Никакой балансировки нет. И дерева никакого нет. Это что-то среднее между фракталом и кривой – spatial filling curve, И их много бывает разных. Смысл один — понижают размерность.
2. Попробуйте Hilbert. Считать его сложнее, но более «близкие» значения в нем расположены «ближе»
3. «Секрет» работы Z-value-ii хорошо описан в интернетах как BIGMIN/LITMAX (https://en.wikipedia.org/wiki/Z-order_curve#Use_with_one-dimensional_data_structures_for_range_searching)
В общем крайне рекомендую активно дружить с этой математикой. Она реально хорошо работает, но надо понимать ограничения.
И не забывать — Z это точка. В то время как R-tree продолжает жрать кактус.
PS: Еще в интернетах можно найти множество более быстрых функций построения Z-кодов
PPS: Некоторые модификации R-tree сами по Z строятся
PPPS: Вэлкам ту зе клаб!
zzeng
10.01.2017 13:31+1по П.1 Z-code — это число, а числа в данном случае мы укладываем в B-дерево.
То, что вы (по видимому) имели ввиду, называется k-d-деревья и это совсем другая история.
И не забывать — Z это точка, прямоугольник — четырехмерная Z точка.
kashey
10.01.2017 13:59+21. В принципе да, на стороне БД это уложиться в B-дерево. Получается достаточно честно. Смотрите на это без БД.
2. Кстати – Z-code, который иногда еще называют «bit interleaving», в принципе KD. Каждый бит режет пространство своей плоскостью.
3. Только вот поиск в окрестности такой четырех-мерной точки будет немного затруднен :)
В общем случае Z(и компания) просто позволяет в начале как-то уложить в некий интервал данные, а потом в нем искать.
При это самый «быстрый» поиск по кодам, когда вам нужна конкретная «ячейка» виртуального quadtree, лучше всего (технически) работает через маску. Вы говорите с чего код должен начинаться – фиксируете первые шаги погружения в дерево, а после некого момента «отпускаете» код, позволяя ему свободно менятся.
Если весь код 4 бита, те 2 уровня, то фиксация 0b1000 с маской 0b0111 матчится на все элементы в левом(или правом) поддереве, те между 0b1000 и 0b1111.
В принципе — это — возможность использовать эти «числа» как NestedSet — одна из основых фичей этих кривых. За прошедшие годы для разных spatial filling придумали очень много наркомании. Текстуры в памяти видеокарты по ним разложены. Gray Code, на котором 99% электроники работает — тоже spatial filling.
К своему сожалению — я далеко не самый лучший рассказчик, но быть может одна старая статейка немного поможет понять, что же я имел в виду.
zzeng
10.01.2017 14:09+2Спасибо за ссылку, в принципе, я в курсе некоторой части этой магии.
И эту статью рассматривал как вводную для описания алгоритма поиска именно по B-дереву, как самому честному способу хранить одномерные данные в (по большому счету) одномерном дисковом пространстве.
Через недельку — другую, добро пожаловать.
А одна старая статейка найдётся не только у вас :)


neolink
Для полноты картины таки стоит проверить решение в лоб с составным индексом
zzeng
глянул одним глазком,
составной индекс занимает 2 Гб,
запрос select count(1)… отрабатывается как index only scan, т.е. без обращения к таблице, читает страниц от 2 до 5 раз меньше по сравнению с X&Y.
Но это скорее хороший пример качественной работы оптимизатора, чем заслуга собственно индекса.