Итак, рассматриваемая здесь задача звучит так: даны угол и точка внутри него. Через эту точку провести отрезки, имеющие концы на сторонах угла, так, чтобы полученный треугольник имел наименьший периметр.

Задачка является частью доказательства задачи Фаньяно.
Первые мысли, которые приходят в голову, это, наверное, построить перпендикуляры (как кратчайшее расстояние до сторон). Отображаем точку симметрично относительно и (получаем точки и ).
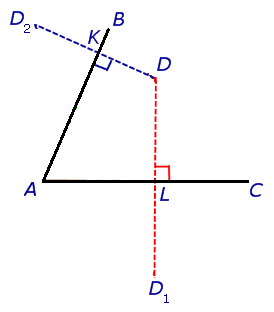
У некоторых сразу же может возникнуть искушение соединить точки пересечения перпендикуляров и сторон угла . После чего появляется ложное впечатления «я сделяль», и кажется, что — это тот самый треугольник.

Всё не так. Тот факт, что две стороны треугольника — кратчайшие (перпендикуляры до прямой), еще не делает периметр треугольника минимальным.
На самом деле поиск треугольника с наименьшим периметром использует утверждение: кратчайшее расстояние между двумя точками – прямая. Дополнительные построения должны привести к тому, чтобы все длины сторон искомого треугольника оказались на прямой. Соединяем точки и . Точки пересечения прямой со сторонами угла и есть оставшиеся искомые вершины треугольника.
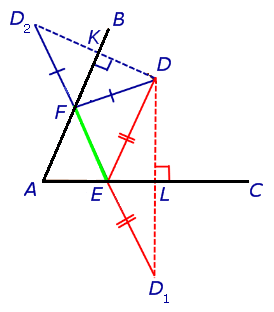
и являются медианами и высотами(точка симметрично отображена относительно сторон угла) треугольников и соответственно, значит треугольники и — равнобедренные. Видно, что периметр треугольника равен длине отрезка . Треугольник с меньшим периметром найден.
Возьмем какие-нибудь другие точки( и ) на сторонах угла.
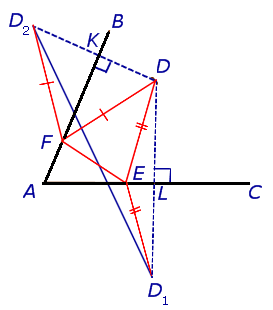
Периметр этого треугольника оказывается больше, чем длина отрезка .
Вот и все. Удачи всем поступающим!
Комментарии (28)

samodum
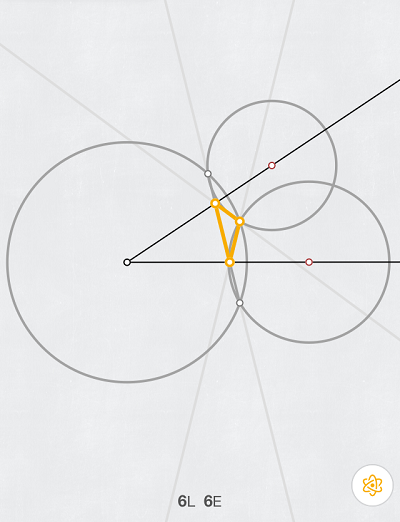
03.06.2017 18:51+4Решал я такую задачку в Euclidea. Под номером 8.1

PoznyakBogdan
04.06.2017 10:39На мой взгляд это наиболее решение, чем то что описывалось в статье.

ser-mk
04.06.2017 13:01Интереснее подробнее узнать какие преимущества это решение обладает по сравнению с доказательством из статьи

IamMaster65
05.06.2017 11:31+1Нет, это три окружности и треугольник. Где тут показано, что это наименьший периметр?
Zenitchik
04.06.2017 00:15+3Пардон за оффтоп, но у меня первой мыслью было вывести функцию периметра треугольника от его стороны, лежащей на одной из сторон данного угла, и минимизировать её.
Спасибо за решение, прочитал с интересом. На досуге повторю, чтобы врубиться в доказательство.

progress_man
04.06.2017 08:42Что-то я не понял, так как были найдены точки D1 и D2?

AnROm
04.06.2017 08:47D1 и D2 строятся симметрично относительно AC и AB: проводятся перпендикуляры к прямым, на продолжении перпендикуляров с другой стороны от прямых откладываются равные отрезки. В данном случае DL = LD1 и DK= KD2.

progress_man
04.06.2017 09:39А, теперь понял, спасибо! Без Вашего разъяснения не понял, что DL = LD1 и DK= KD2

sanu001
04.06.2017 17:57Эту задачу мне задали на вступительных экзаменах на Физтех в 1984 году — дали 5 минут на решение.

maisvendoo
04.06.2017 21:07Классная задачка
Задачка из той же оперы, но в 3DВнутри прямоугольной комнаты, имеющей 30 футов в длину и по 12 футов в ширину и высоту, на середине одной из торцовых стен в 1 футе от потолка сидит паук (точка А). Муха сидит на середине противоположной стены в 1 футе от пола (точка В). Каково кратчайшее расстояние, каким паук может добраться до неподвижной мухи? Разумеется, паук никогда не падает и не использует для передвижения паутины.


LoadRunner
05.06.2017 08:36А почему задачка из той же оперы? Там есть какой-то скрытый подвох и неочевидное решение? Она-то как раз в лоб легко решается через построение перпендикуляров.

Bronx
05.06.2017 08:39Если у вас получилось «42», то это ответ к совсем другой задаче :) У этой правильный ответ — «40»

LoadRunner
05.06.2017 08:41Так в чём же подвох тогда?

Bronx
05.06.2017 08:48Сделайте разные развертки параллелепипеда, поищите возможные «кратчайшие» (т.е. прямолинейные) пути на развёртке (их там больше одного) и сравните их длины.

LoadRunner
05.06.2017 09:41Всего возможны две принципиально разные развёртки (другие зеркальны первым двум). По одной из них кратчайшее расстояние — путь от паука до пола вниз по стене, потом до стены, потом до мухи вверх по стене. Это 42.
По другой — гипотенуза треугольника с катетами 42 и 10. Но гипотенуза будет уже больше 42, так что этот вариант отметаем.
Я опять не понимаю, что упускаю из вида и как у Вас получается 40.
AnROm
05.06.2017 10:05+3


LoadRunner
05.06.2017 10:12Мой мозг сломался так же, как эта прямая линия. Теперь вижу, что развёрток больше двух :)

master65
05.06.2017 19:52Начал читать википедию. Очнулся вечером. В школе явно не было такой геометрии


maximw
Что-то не совсем понял доказательство минимальности использованного решения.
UPD. Понял.
romankonstant
Что-то не совсем понял, когда задачи для 9 класса стали появляться на Хабре.
UPD. Я шучу, конечно, сам когда-то сидел ломал над ней голову.
Bronx
В принципе, это оптический метод: зная, что из всех альтернативных путей свет выбирает кратчайший, мы можем представить, что AB и АС — это отражающие поверхности, и искомый треугольник будет образован лучом света, испускаемым из D и попадающим обратно в D. Решением будет путь, при котором угол падения луча DF (или DL) равен углу отражения луча FE (или LF). D1 и D2 — это изображения D в зеркалах.