Девушка: Нарисуй дерево.
Программист: (рисует бинарное дерево)
Девушка: Нет, другое.
Программист: Я и красно-черное дерево могу нарисовать.
Итак, сегодня хочу немного рассказать о красно-черных деревьях. Рассказ будет кратким, без рассмотрения алгоритмов балансировки при вставке/удалении элементов в красно-черных деревьях.
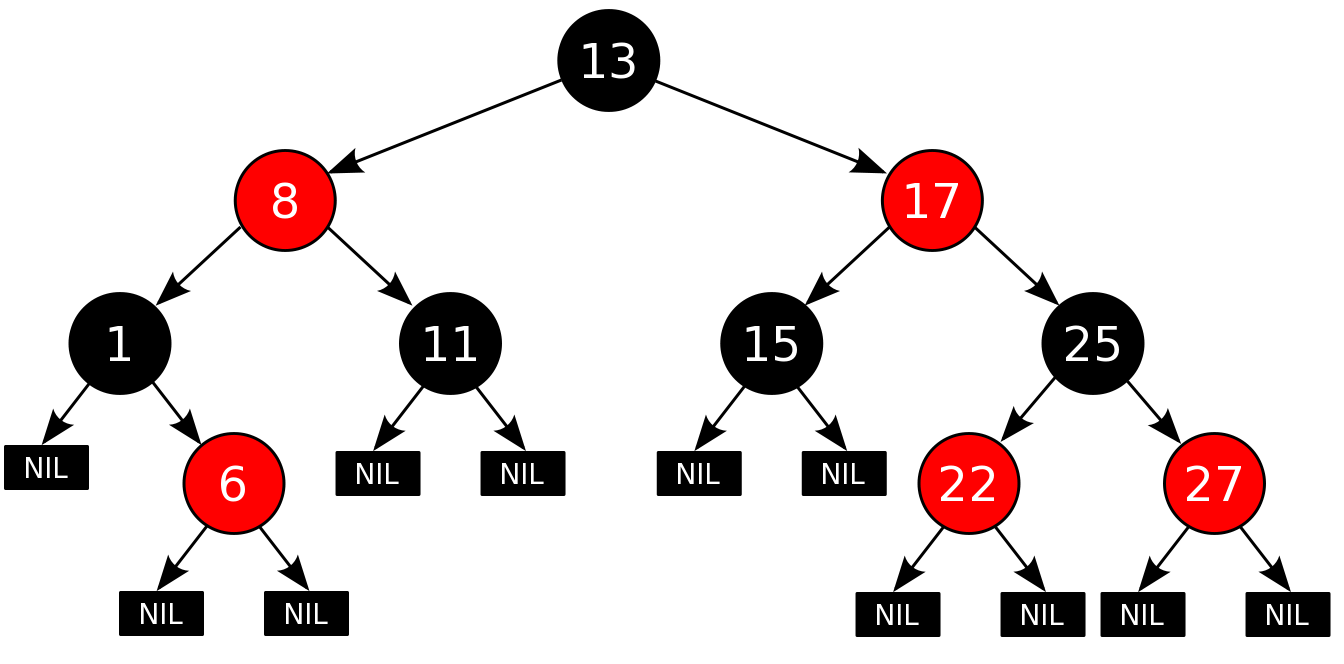
Красно-черные деревья относятся к сбалансированным бинарным деревьям поиска.
Как бинарное дерево, красно-черное обладает свойствами:
1) Оба поддерева являются бинарными деревьями поиска.
2) Для каждого узла с ключом выполняется критерий упорядочения:
ключи всех левых потомков <= < ключи всех правых потомков
(в других определениях дубликаты должны располагаться с правой стороны либо вообще отсутствовать).
Это неравенство должно быть истинным для всех потомков узла, а не только его дочерних узлов.
Свойства красно-черных деревьев:
1) Каждый узел окрашен либо в красный, либо в черный цвет (в структуре данных узла появляется дополнительное поле – бит цвета).
2) Корень окрашен в черный цвет.
3) Листья(так называемые NULL-узлы) окрашены в черный цвет.
4) Каждый красный узел должен иметь два черных дочерних узла. Нужно отметить, что у черного узла могут быть черные дочерние узлы. Красные узлы в качестве дочерних могут иметь только черные.
5) Пути от узла к его листьям должны содержать одинаковое количество черных узлов(это черная высота).
Ну и почему такое дерево является сбалансированным?
Действительно, красно-черные деревья не гарантируют строгой сбалансированности (разница высот двух поддеревьев любого узла не должна превышать 1), как в АВЛ-деревьях. Но соблюдение свойств красно-черного дерева позволяет обеспечить выполнение операций вставки, удаления и выборки за время . И сейчас посмотрим, действительно ли это так.
Пусть у нас есть красно-черное дерево. Черная высота равна (black height).
Если путь от корневого узла до листового содержит минимальное количество красных узлов (т.е. ноль), значит этот путь равен .
Если же путь содержит максимальное количество красных узлов ( в соответствии со свойством ), то этот путь будет равен .
То есть, пути из корня к листьям могут различаться не более, чем вдвое (, где h — высота поддерева), этого достаточно, чтобы время выполнения операций в таком дереве было
Как производится вставка?
Вставка в красно-черное дерево начинается со вставки элемента, как в обычном бинарном дереве поиска. Только здесь элементы вставляются в позиции NULL-листьев. Вставленный узел всегда окрашивается в красный цвет. Далее идет процедура проверки сохранения свойств красно-черного дерева .
Свойство 1 не нарушается, поскольку новому узлу сразу присваивается красный цвет.
Свойство 2 нарушается только в том случае, если у нас было пустое дерево и первый вставленный узел (он же корень) окрашен в красный цвет. Здесь достаточно просто перекрасить корень в черный цвет.
Свойство 3 также не нарушается, поскольку при добавлении узла он получает черные листовые NULL-узлы.
В основном встречаются 2 других нарушения:
1) Красный узел имеет красный дочерний узел (нарушено свойство ).
2) Пути в дереве содержат разное количество черных узлов (нарушено свойство ).
Подробнее о балансировке красно-черного дерева при разных случаях (их пять, если включить нарушение свойства ) можно почитать на wiki.
Это вообще где-то используется?
Да! Когда в институте на третьем курсе нам читали «Алгоритмы и структуры данных», я и не могла представить, что красно-черные деревья где-то используются. Помню, как мы не любили тему сбалансированных деревьев. Ох уж эти родственные связи в красно-черных деревьях («дядя», «дедушка», «чёрный брат и
Это все, что я хотела рассказать.
Комментарии (42)
mayorovp
10.06.2017 13:53-12В нормальных ассоциативных массивах используются хеш-таблицы, а не деревья.
mayorovp
11.06.2017 09:31+2Хорошо, изменю формулировку, если эта не нравится.
Хеш-таблицы работают быстрее деревьев, а потому для ассоциативных массивов предпочтительнее использовать именно их.

Dark_Daiver
11.06.2017 09:43+1На самом деле все сильно зависит от конкретного случая.
Скажем, если вам требуется держать много небольших ассоциативных массивов, то хэш-таблицы возможно не особо хороший вариант, т.к. потребляют относительно много памяти.
Large
11.06.2017 12:03+1если вам нужно реализовать неизменяемые структуры данных то без деревьев они будут потреблять слишком много памяти. сортированные таблицы тоже без деревьев нормально не сделаешь.
alexeykuzmin0
13.06.2017 16:48Это не всегда (хотя и чаще всего) верно. Простой пример: ассоциативный массив из небольшого количества элементов с длинным ключом. Набросал эксперимент: сравнение std::map и std::unordered_map для контейнера из 1 000 элементов, ключом в которых является случайная строка длиной 100 000, а значение — символ:
Кодconst int COUNT = 1000; const int LENGTH = 100 * 1000; const int QUERIES = 10; string ss[COUNT]; for (int i = 0; i < COUNT; ++i) { ss[i] = ""; for (int j = 0; j < LENGTH; ++j) { ss[i] += (char)('a' + rand() % 10); } } double start = clock(); unordered_map<string, char> um; for (int q = 0; q < QUERIES; ++q) { for (int i = 0; i < COUNT; ++i) { um[ss[i]] = ss[i][0]; } } cout << (clock() - start) / CLOCKS_PER_SEC << endl; start = clock(); map<string, char> m; for (int q = 0; q < QUERIES; ++q) { for (int i = 0; i < COUNT; ++i) { m[ss[i]] = ss[i][0]; } } cout << (clock() - start) / CLOCKS_PER_SEC << endl;
MrShoor
14.06.2017 06:15Есть такая штука, как collision attack. Поэтому для всех ассоциативных контейнеров, смотрящих наружу — предпочительнее использовать деревья. Это например касается баз данных, любого серверного бек-энда принимающего пользовательские данные, объектов уровня ядра ОС и т.п.
А некоторые неосторожные хештаблицы умудряются сами себе устроить такой collision attack. Совсем недавно так облажались:
1. Swift
2. Rust
3. Delphimayorovp
14.06.2017 06:23+2Для защиты от такой атаки достаточно выбирать случайную хеш-функцию. Или можно использовать деревья уже внутри корзин хеш-таблицы, как делает стандартная библиотека Java

MrShoor
14.06.2017 06:57Это решение из разряда: «мне повезет». Коллизии заложены в самой природе хешфункции, и попытки замаскировать проблему не решат её.
alexeykuzmin0
14.06.2017 12:06Вероятность того, что «не повезет» обычно экспоненциально (или быстрее) уменьшается с ростом размера входных данных. Так что можно и рискнуть — все равно шансы того, что для более или менее разумного размера данных нам «не повезет» хоть за миллиард лет работы алгоритма, крайне малы.

MikeLP
10.06.2017 14:03+6Статья хорошая, дерево нужное (потому что многие, кому доводилось хранить сколь угодно большую вложенную структуру, интересовались хоть раз как хранить и опимизировать эту структуру, уменьшить время вствавки и т.д.), формулы понятные. Но все же хотелось бы обьяснения на пальцах без подробных формул, потому что, например, я лично приблизительно интуитивно понимаю как оно работает, но академические выражения «черная высота» не добавляет ясности. И в конце получился не очень красивый итог — аля шо не поняли лошки эти сраные деревья — а кто-то взял и понял. Лол.
Надеюсь у вас будет еще время сделать более подробную статью.Large
11.06.2017 12:14посмотрите на авл-деревья они более простые (разница в длине веток не должна быть больше одного элемента) и на реальных данных обычно работают быстрее (удаление обходится дороже но если мало удаляете то можно смело использовать). идея везде до ужаса простая — если у вас есть список N элементов, то чтоб найти какой-то конкретный элемент вам нужно в худшем случае пробежаться от начала и до конца списка, то есть пройти N шагов, а если вы тот же список разветвили (с помощью операции сравнения) и превратили в дерево — то уже нужно пройти log N шагов. Любая операция — вставка или удаление должны менять дерево так, чтоб оно оставалось ветвистым (для авл деревьев — разница между высотой веток не больше 1 элемента, для красно-черных — не больше чем в два раза (потому их и красят в два цвета)) и не нарушалось правило поиска.

konshyn
10.06.2017 16:23+10Рассказ будет кратким, без рассмотрения алгоритмов балансировки при вставке/удалении элементов в красно-черных деревьях.
Т.е. самое важное, благодаря чему используется это дерево фактически везде в STL, не рассматривается?
Имхо, эту статью можно просто заменить ссылкой на википедию.

niamster
10.06.2017 16:33+11Красно-черные деревья не интуитивны, но если понять, что они эквиваленты 2-3 деревьям(которые воспринимаются проще) то все становится на свои места.
Отличное объяснение от автора красно-черных деревьев Р. Седжвика на портале Принстонского университета.
Для полноты статьи добавьте алгоритм удаления ячейки. Это самая захватывающая часть.

fRoStBiT
10.06.2017 18:13+6Открывая статью с таким заголовком, думал, что наконец-то пойму, как происходит удаление чёрного листа.
Ан нет…
Andrey_Solomatin
10.06.2017 20:58+2Визуализация вставки и удаления: https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
Если поставить на паузу и идти по шагам, там будет коротки пояснительный текст.

babylon
10.06.2017 19:11
khim
10.06.2017 20:02+4ключи всех левых потомков <= k < ключи всех правых потомков
Распространённая ошибка. Рассмотрите дерево из миллиона одинаковых элементов и попытайтесь его сбалансировать. Хорошо получится?
Либо <= дважды, либо < дважды (а одинаковые элементы запрещены), пожалуйста.

grossws
10.06.2017 23:50+3Так, например, ассоциативные массивы в большинстве библиотек реализованы именно через красно-черные деревья.
А можно подтверждающую статистику? Ну, в STL map по умолчанию такой. В python, ruby, perl и lua по умолчанию hash map'ы. В java "по умолчанию" варианта нет, но присутствуют и hash map и tree map.

Maccimo
11.06.2017 15:40+4В военное время HashMap может стать немного красно-чёрным.

grossws
11.06.2017 18:46Только в тяжёлых бинах, большая же часть останется нормальной человеческой hash-таблицей с поиском/вставкой за O(1) с худшим вариантом на уровне O(log N).
И то, это детали имплементации, позволяющие иметь нормальную производительность при сильно неудачном сочетании данных и хэш-функции, когда много данных (или все) попадают в один бин.

workmi
11.06.2017 00:22-2а вот если к цвету прибавить вес(дальность до предка)… то брюки превращаются… брюки превращаются…

IvanTamerlan
11.06.2017 18:03при перебалансировке веса нужно пересчитывать. Выше уже выкладывали визуализацию, в которой при изменениях идут повороты вплоть до смены корня. Поменялся корень — нужно веса пересчитать, что сказывается на производительности.
tangro
12.06.2017 13:15-3Красно-чёрным деревьям, как мне кажется, очень сильно мешает именно использование терминов «красный» и «чёрный». Я хорошо помню эту лекцию в университете «А теперь нарисуем дерево с черной вершиной и двумя красными детьми...» — и вся аудитория в ступоре, потому что откуда же у студентов с собой на лекции цветные карандаши или ручки? Во всей остальной дискретке используются какие-нибудь индексы, типы, подтипы — и всё понятно. А тут откуда-то взялись цвета, которые ещё и сочетаться должны в определённом порядке. Мы что, на лекции по моде в ПТУ легкой промышленности?

Maccimo
12.06.2017 15:02+7Спасибо вам, теперь я понял, почему квантовая физика так сложна!
Ведь там у кварков мало того, что цвет, так ещё и аромат есть. Откуда же у студентов с собой на лекции несколько флаконов духов возьмутся? Мы что, в парфюмерном магазине?tangro
13.06.2017 12:00-2А в чём сарказм? Типа квантовая физика не сложна? Или типа неуместные аналогии делают её проще?

aristarh1970
13.06.2017 00:47+1Не понял, а обозначить «красную вершину» кружочком, а «черную вершину» кружочком с крестиком нельзя?
tangro
13.06.2017 11:59-2Можно. Но это примерно как назвать «длиной» переменную, которая означает ширину и написать рядом комментарий, что это на самом деле длина. Будет работать, но добавляет лишний уровень косвенности и запутанности.

aristarh1970
13.06.2017 17:50+3Вы передергиваете.
Если БЫ в алгоритме наравне с «красными/черными» вершинами присутствовали еще «белые» и «отмеченные крестиком» вершины, то ваша аналогия была бы уместана.
А так мы имееи ровно ДВА типа вершин, к которым применить краткую удобную систему условносных обозначений не составит труда.
Ни для записи, ни для понимания.
tangro
13.06.2017 22:03-3Ну ок, а в двоичной системе счисления мы, например, имеем две цифры — 0 и 1. Можно было бы назвать эти сущности названиями цветов, нот, ароматов или сказочных животных. Суть была бы та же — «два типа». Но мы их всё же называем цифрами 0 и 1. Красно-чёрные деревья очень сильно «выбиваются». Ну нет таких обозначений в векторах, матрицах, графах, уравнениях, графиках и всей прочей математике до и после этих цветных деревьев.
mayorovp
13.06.2017 23:45+1Напротив, алгоритмы на графах (а деревья — раздел графов) очень часто оперируют понятием цвета.
А уж графики-то всегда даже визуально раскрашивать стараются.
alexeykuzmin0
14.06.2017 12:17Вы буквально воспринимаете всю специфическую графовую терминологию, что ли? Хорошо, что вам лектор не говорил фраз типа «и тут мы левого сына присваиваем правому соседу», совсем бы крыша поехала.
tangro
14.06.2017 16:44-1Говорил, конечно, крыша не поехала. Просто неудобная терминология, я же не говорю, что она сложная или что алгоритмы не работают. Названо просто глупо, а сама структура данных хорошая.


frees2
Менюшку такую можно сделать, с двумя цветами, больше будет отвлекать. Прямо в шапке страницы. Сейчас шапки на пол экрана, а так хоть функциональность будет.