01.11.2017 16:24
The_Freeman 33 4900 Источник

Библиотека RandLib позволяет работать с более чем 50 известными распределениями, непрерывными, дискретными, двумерными, циклическими и даже одним сингулярным. Если нужно какое-нибудь распределение, то вводим его имя и добавляем суффикс Rand. Заинтересовались?

Генераторы случайных величин


Если мы хотим сгенерировать миллион случайных величин из нормального распределения, используя стандартную библиотеку шаблонов C++, мы напишем что-нибудь вроде

std::random_device rd;
std::mt19937 gen(rd());
std::normal_distribution<> X(0, 1);
std::vector<double> data(1e6);
for (double &var : data)
   var = X(gen);

Шесть интуитивно не очень понятных строчек. RandLib позволяет их количество сократить вдвое. 

NormalRand X(0, 1);
std::vector<double> data(1e6);
X.Sample(data);

Если нужна лишь одна случайная стандартная нормально распределённая величина, то это можно сделать в одну строчку

double var = NormalRand::StandardVariate();

Как можно заметить, RandLib избавляет пользователя от двух вещей: выбора базового генератора (функции, возвращающей целое число от 0 до некого RAND_MAX) и выбора стартовой позиции для случайной последовательности (функция srand()). Сделано это во имя удобства, так как многим пользователям этот выбор скорее всего ни к чему. В подавляющем большинстве случаев случайные величины генерируются не непосредственно через базовый генератор, а через случайную величину U, распределенную равномерно от 0 до 1, которая уже зависит от этого базового генератора. Для того, чтобы изменить способ генерации U, нужно воспользоваться следующими директивами:

#define UNIDBLRAND // генератор дает большее разрешение за счет комбинации двух случайных чисел
#define JLKISS64RAND // генератор дает большее разрешение за счет генерации 64-битных целых чисел
#define UNICLOSEDRAND // U может вернуть 0 или 1
#define UNIHALFCLOSEDRAND // U может вернуть 0, но никогда не вернет 1

По умолчанию U не возвращает ни 0, ни 1.

Скорость генерации


В последующей таблице предоставлено сравнение времени на генерацию одной случайной величины в микросекундах.

Характеристики системы
Ubuntu 16.04 LTS
Процессор: Intel Core i7-4710MQ CPU @ 2.50GHz ? 8
Тип ОС: 64-разрядная

Распределение STL RandLib

$\mathcal{U}(0, 1)$

 0.017 ?s 0.006 ?s

$\mathcal{N}(0, 1)$

 0.075 ?s 0.018 ?s

$\mathrm{Exp}(1)$

 0.109 ?s 0.016 ?s

$\mathrm{Cauchy}(0, 1)$

 0.122 ?s 0.024 ?s

$\mathrm{Log-Normal}(0, 1)$

 0.158 ?s 0.101 ?s

$\mathrm{Weibull}(1, 1)$

 0.108 ?s 0.019 ?s

Больше сравнений
Гамма-распределение:

$\Gamma(0.1, 1)$

 0.207 ?s 0.09 ?s

$\Gamma(1, 1) \sim \mathrm{Exp}(1) $

 0.161 ?s 0.016 ?s

$\Gamma(1.5, 1)$

 0.159 ?s 0.032 ?s

$\Gamma(2, 1)$

 0.159 ?s 0.03 ?s

$\Gamma(5, 1)$

 0.159 ?s 0.082 ?s
Распределение Стьюдента:

$\mathcal{t}(0.1)$

 0.248 ?s 0.107 ?s

$\mathcal{t}(1)\sim \mathrm{Cauchy}(0, 1) $

 0.262 ?s 0.024 ?s

$\mathcal{t}(1.5)$

 0.33 ?s 0.107 ?s

$\mathcal{t}(2)$

 0.236 ?s 0.039 ?s

$\mathcal{t}(5)$

 0.233 ?s 0.108 ?s
Распределение Фишера:

$\mathrm{F}(1, 1)$

 0.361 ?s 0.099 ?s

$\mathrm{F}(2, 2)$

 0.319 ?s 0.013 ?s

$\mathrm{F}(3, 3)$

 0.314 ?s 0.027 ?s

$\mathrm{F}(1, 10)$

 0.331 ?s 0.169 ?s

$\mathrm{F}(5, 1)$

 0.333 ?s 0.177 ?s
Биномиальное распределение:

$\mathrm{Bin}(10, 0.5)$

 0.655 ?s 0.033 ?s

$\mathrm{Bin}(10, 0.7)$

 0.444 ?s 0.093 ?s

$\mathrm{Bin}(100, 0.07)$

 0.873 ?s 0.197 ?s
Распределение Пуассона:

$\mathrm{Po}(1)$

 0.048 ?s 0.015 ?s

$\mathrm{Po}(15)$

 0.446 ?s 0.105 ?s
Отрицательное биномиальное распределение:

$\mathrm{NB}(1, 0.5) \sim \mathrm{Geometric}(0.5) $

 0.297 ?s 0.019 ?s

$\mathrm{NB}(10, 0.5)$

 0.587 ?s 0.257 ?s

$\mathrm{NB}(100, 0.05)$

 1.017 ?s 0.108 ?s


Как можно увидеть, RandLib иногда в 1.5 раза быстрее, чем STL, иногда в 2, иногда в 10, но никогда медленнее.

Функции распределения, моменты и прочие свойства


Помимо генераторов RandLib предоставляет возможность рассчитать функции вероятности для любого из данных распределений. Например, чтобы узнать вероятность того, что случайная величина с распределением Пуассона с параметром a примет значение k нужно вызвать функцию P.

int a = 5, k = 1;
PoissonRand X(a);
X.P(k); // 0.0336897

Так сложилось, что именно заглавная буква P обозначает функцию, возвращающую вероятность принятия какого-либо значения для дискретного распределения. У непрерывных распределений эта вероятность равна нулю почти всюду, поэтому вместо этого рассматривается плотность, которая обозначается буквой f. Для того, чтобы рассчитать функцию распределения, как для непрерывных, так и для дискретных распределений нужно вызвать функцию F:

double x = 0;
NormalRand X(0, 1);
X.f(x); // 0.398942
X.F(x); // 0

Иногда нужно посчитать функцию 1-F(x), где F(x) принимает очень маленькие значения. В таком случае, чтобы не потерять точность следует вызывать функцию S(x).

Если же нужно посчитать вероятности для целого набора значений, то для этого нужно вызвать функции:

//x и y - std::vector
X.CumulativeDistributionFunction(x, y); // y = F(x)
X.SurvivalFunction(x, y); // y = S(x)
X.ProbabilityDensityFunction(x, y) // y = f(x) - для непрерывных
X.ProbabilityMassFunction(x, y) // y = P(x) - для дискретных

Квантиль — это функция от p, возвращающая x, такой что p = F(x). Соответствующие реализации есть также в каждом конечном классе RandLib, соответствующем одномерному распределению:

X.Quantile(p); // возвращает x = F^(-1)(p)
X.Quantile1m(p); // возвращает x = S^(-1)(p)
X.QuantileFunction(x, y) // y = F^(-1)(x)
X.QuantileFunction1m(x, y) // y = S^(-1)(x)

Иногда вместо функций f(x) или P(k) нужно достать соответствующие им логарифмы. В таком случае лучше всего воспользоваться следующими функциями:

X.logf(k); // возвращает x = log(f(k))
X.logP(k); // возвращает x = log(P(k))
X.LogProbabilityDensityFunction(x, y) // y = logf(x) - для непрерывных
X.LogProbabilityMassFunction(x, y) // y = logP(x) - для дискретных

Также RandLib предоставляет возможность рассчитать характеристическую функцию:

$\phi_X(t)=\mathbb{E}[e^{itX}]$



X.CF(t); // возвращает комплексное значение \phi(t)
X.CharacteristicFunction(x, y) // y = \phi(x)

Кроме того, можно легко достать первые четыре момента или математическое ожидание, дисперсию, коэффициенты асимметрии и эксцесса. Кроме того, медиану (F^(-1)(0.5)) и моду (точку, где f или P принимает наибольшее значение).

LogNormalRand X(1, 1);
std::cout << " Mean = " << X.Mean()
          << " and Variance = " << X.Variance()
          << "\n Median = " << X.Median()
          << " and Mode = " << X.Mode()
          << "\n Skewness = " << X.Skewness()
          << " and Excess kurtosis = " << X.ExcessKurtosis();



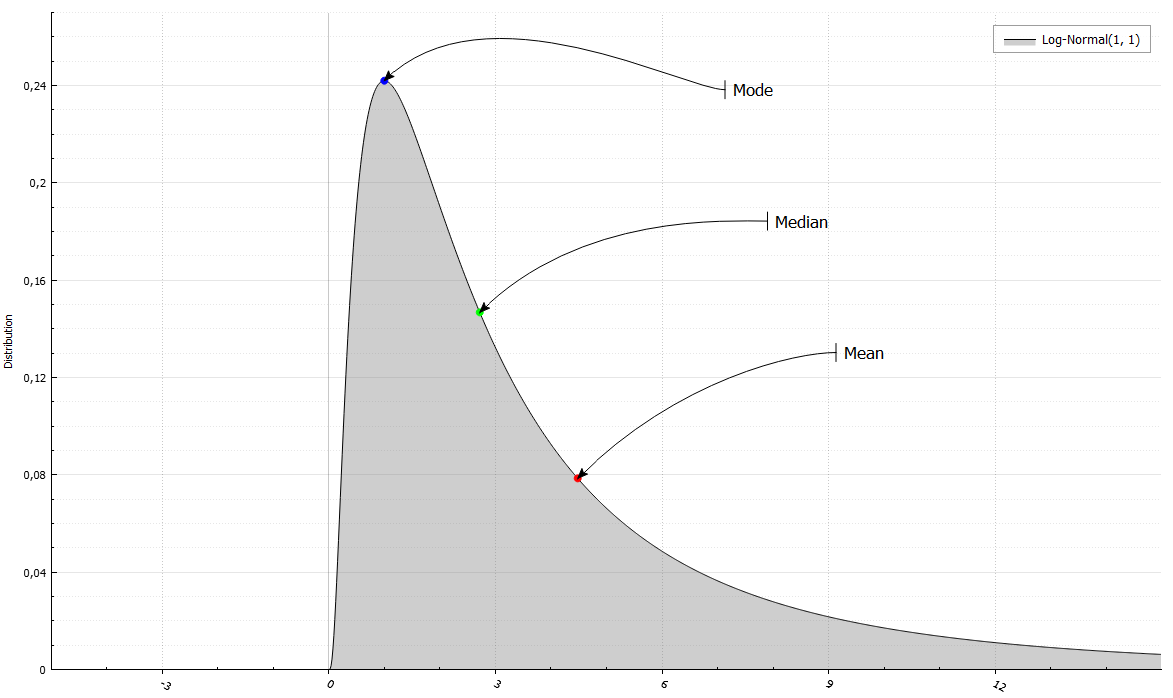
Mean = 4.48169 and Variance = 34.5126
Median = 2.71828 and Mode = 1
Skewness = 6.18488 and Excess Kurtosis = 110.936

Оценки параметров и статистические тесты


От теории вероятностей к статистике. Для некоторых (пока не для всех) классов есть функция Fit, которая задает параметры, соответствующие некоторой оценке. Рассмотрим на примере нормального распределения:

using std::cout;
NormalRand X(0, 1);
std::vector<double> data(10);
X.Sample(data);
cout << "True distribution: " << X.Name() << "\n";
cout << "Sample: ";
for (double var : data)
    cout << var << "  ";

Мы сгенерировали 10 элементов из стандартного нормального распределения. На выходе должны получить что-нибудь вроде:

True distribution: Normal(0, 1)
Sample: -0.328154  0.709122  -0.607214  1.11472  -1.23726  -0.123584  0.59374  -1.20573  -0.397376  -1.63173

Функция Fit в данном случае задаст параметры, соответствующие оценке максимального-правдоподобия:

X.Fit(data);
cout << "Maximum-likelihood estimator: " << X.Name(); // Normal(-0.3113, 0.7425)

Как известно, максимальное правдоподобие для дисперсии нормального распределения даёт смещенную оценку. Поэтому в функции Fit есть дополнительные параметр unbiased (по умолчанию false), которым можно настраивать смещенность / несмещенность оценки.

X.Fit(data, true);
cout << "UMVU estimator: " << X.Name(); // Normal(-0.3113, 0.825)

Для любителей Байесовской идеологии также есть и Байесовская оценка. Структура RandLib позволяет очень удобно оперировать априорным и апостериорным распределениями:

NormalInverseGammaRand prior(0, 1, 1, 1);
NormalInverseGammaRand posterior = X.FitBayes(data, prior);
cout << "Bayesian estimator: " << X.Name(); // Normal(-0.2830, 0.9513)
cout << "(Posterior distribution: " << posterior.Name() << ")"; //  Normal-Inverse-Gamma(-0.2830, 11, 6, 4.756)

Тесты


Как узнать, что генераторы, как и функции распределения возвращают правильные значения? Ответ: сравнить одни с другими. Для непрерывных распределений реализована функция, проводящая тест Колмогорова-Смирнова на принадлежность данной выборки соответствующему распределению. На вход функция KolmogorovSmirnovTest принимает порядковую статистику и уровень \alpha, а на выход возвращает true, если выборка соответствует распределению. Дискретным распределениям соответствует функция PearsonChiSquaredTest.

Заключение


Данная статья специально написана для части хабрасообщества, интересующейся подобным и способной оценить. Разбирайтесь, ковыряйтесь, пользуйтесь на здоровье. Основные плюсы:

  • Бесплатность
  • Открытый исходный код
  • Скорость работы
  • Удобство пользования (моё субъективное мнение)
  • Отсутствие зависимостей (да-да, не нужно ничего)

Ссылка на релиз.

Комментарии (33)


  1. mayorovp
    01.11.2017 19:34
    #10502328
    +1

    А какой define ставить если нужен детерминированный генератор?


  1. oYASo
    01.11.2017 20:52
    #10502410

    О, средства для статмоделирования мы любим! На первый взгляд библиотека выглядит очень хорошо, код написан понятно и качественно, приятно читать. Будем тестировать!


  1. Sdima1357
    01.11.2017 21:42
    #10502452

    1
    «RandLib избавляет пользователя от двух вещей: выбора базового генератора (функции, возвращающей целое число от 0 до некого RAND_MAX) и выбора стартовой позиции для случайной последовательности (функция srand()). Сделано это во имя удобства, так как многим пользователям этот выбор скорее всего ни к чему.»

    — Не согласен.Для отладки очень часто нужна именно повторяемость.

    2
    Могут быть проблемы со статическими переменными в функциях BasicRandGenerator<..>::Variate() в многопоточной среде, лучше сделать их членами класса.


    1. Dark_Daiver
      01.11.2017 23:32
      #10502578
      +1

      >Не согласен.Для отладки очень часто нужна именно повторяемость.
      Поддерживаю, фактически это сильно ограничивает использование библиотеки во всяких научных вычислениях


    1. Sdima1357
      01.11.2017 23:37
      #10502584

      Автору
      Вообще — типичный код для математика: отличная алгоритмическая работа и значительно более слабая (хотя и неплохая) реализация. Фунцию Variate поправьте обязательно, однозначно будет проблема со скоростью (конфликт read-modify-write на общей памяти)
      Кроме того, статические переменные затрудняют работу оптимизатора если Вы используете более одного экземпляра класса


    1. The_Freeman Автор
      02.11.2017 10:53
      #10502954

      1. Согласен с тем, что нужно добавить функционал на подобие srand. Но не стоит заставлять пользователя всегда его использовать. В целом, Вы правы.

      2. Наверное, еще лучше их сделать static thread_local. Однако это сильно повлияет на скорость. В таком случае надо предоставлять выбор. В конце концов, rand() сделан по схожему принципу и тоже не является потоко-безопасным.


      1. Sdima1357
        02.11.2017 13:42
        #10503272
        +1

        rand() — отвратная и древняя функция,static thread_local — не нужно, нужны именно переменные члены класса или структуры. Еще раз, статические переменные затрудняют работу оптимизатора если Вы используете более одного экземпляра класса даже в одном потоке.


      1. Sdima1357
        02.11.2017 14:00
        #10503296
        +1

        Возьмите код отсюда
        * brief Tiny Mersenne Twister only 127 bit internal state
        *
        * author Mutsuo Saito (Hiroshima University)
        * author Makoto Matsumoto (University of Tokyo)

        github.com/MersenneTwister-Lab/TinyMT
        На моей машине дает (3.2 GHz ) 2.7 ns per uniform number и это лучший генератор который я видел


        1. DaylightIsBurning
          02.11.2017 15:52
          #10503532

          вот тут обещают от 0.64 ns: 1/(50Gb/s/32bit)=0.64ns


          1. Sdima1357
            02.11.2017 18:47
            #10503796

            лучший Mersenne Twister генератор который я видел :). А вообще спасибо, посмотрю обязательно. Мне скорость и качество очень критичны(RANSAC like code).


          1. Sdima1357
            02.11.2017 20:06
            #10503876

            1.1 ns (rnd32) бит на том же тесте: habrahabr.ru/post/323158/#comment_10503460


  1. AutomaticSearches
    02.11.2017 06:53
    #10502770

    Да это прикольная штука, правда мне не доводилось сталкиваться с задачами в которых нужен бы что-то большее чем rand. Но вот те кто пишут казино им там законы распределения вероятности явно пригодятся.


    1. domix32
      02.11.2017 11:17
      #10503006

      Казино на бэкэнде маловероятно используют С++.


      1. AutomaticSearches
        02.11.2017 17:13
        #10503658

        Ну не только с# и java свет един.


        1. domix32
          02.11.2017 21:39
          #10503978

          Скорость разработки при большей отказоустойчивости в данном случае выше необходимости иметь оптимальное потребление памяти и бОльшую скорость вычислений. Кроме того легальные букмекерки использую источники событий данных с околоистинными рандомами физического мира, которые были некогда замерены, дабы владельцы не имели возможности смухлевать или подкрутить рандомы в свою пользу. Так что для казино данная конкретная либа врядли пригодится.


  1. firegurafiku
    02.11.2017 07:08
    #10502776

    Я не специалист в матстатистике, но если бы мне понадобилась подобная библиотека для чего-то серьёзного, то первым делом я бы поинтересовался качеством полученных распределений. Они какие-нибудь тесты на случайность проходят? Всякие NIST и Die Hard там.


    И ещё: в C++17 точно никак нельзя было обойтись без макросов? Вы бы их хотя бы префиксом RANDLIB_ снабдили, а всё остальное запихнули в неймспейс.


    1. The_Freeman Автор
      02.11.2017 11:10
      #10502982

      По умолчанию, основной генератор — это JKISS из статьи Good Practice in (Pseudo) Random Number Generation for Bioinformatics Applications. Он проходит все DieHard тесты. Генераторы для прочих распределений используют именно его.

      Грешен, но упомянутые макросы единственные на всю библиотеку. Знаю, какая на них реакция в целом, но в данном случае их использование было удобно мне как разработчику, и виделось удобным пользователю. Про префикс Вы правы, будет учтено.


      1. firegurafiku
        02.11.2017 13:00
        #10503186
        +1

        Ещё вопрос возник: если я вдруг захочу генерировать числа точности выше двойной (например, такие, как в boost::multiprecision), ваша библиотека справится? А то я посмотрел исходники класса NormalRand, а там везде double захардкожен. И если такая возможность есть, просто я проглядел, не пострадают ли при этом статистические характеристики распределений?


        1. The_Freeman Автор
          02.11.2017 13:06
          #10503198

          Пока что это не поддерживается. Но предложение хорошее!


  1. Effolkronium
    02.11.2017 08:54
    #10502838

    Лучше попробуйте мою либу, C++11, header-only, всё на шаблончиках, никаких макросов. Поддерживает многопоточность, и какие угодно распределения через шаблонные параметры, и конечто же много юнит тестов. Делает работу с рандомом проще в 100 раз.

    Узнать больше:
    github.com/effolkronium/random


    1. The_Freeman Автор
      02.11.2017 11:14
      #10502994

      Ваша библиотека выглядит прелестно. Но это лишь обертка вокруг функций std, а RandLib в свою очередь полная альтернатива стандартной библиотеке. Кроме того, у Вас только генераторы. Возможности RandLib куда шире (функции распределения, моменты и т.п.). Тут не уложиться в header-only.


      1. Effolkronium
        02.11.2017 13:34
        #10503258

        Обёртка не только вокруг std, в шаблонные параметры можно закинуть любые генераторы и распределители


  1. Jamdaze
    02.11.2017 12:23
    #10503130
    +2

    А причём тут с++17?
    Макросы, непойми какая поддержка многопоточности. Оно вобще не упадёт если в несколько потоков генерировать случайные последовательности?


    1. The_Freeman Автор
      02.11.2017 13:01
      #10503188

      Про поддержку многопоточности в статье указано не было, но в дальнейших версиях это будет учтено. Смысл Вашего комментария лишь в том чтобы повторить вышесказанное.
      По поводу С++17, он в основном был нужен ввиду появившихся в нем специальных математических функций.


  1. DaylightIsBurning
    02.11.2017 13:47
    #10503274
    +1

    #define UNIDBLRAND // генератор дает большее разрешение за счет комбинации двух случайных чисел
#define JLKISS64RAND // генератор дает большее разрешение за счет генерации 64-битных целых чисел
#define UNICLOSEDRAND // U может вернуть 0 или 1
#define UNIHALFCLOSEDRAND
    А если мне нужно два числа подряд, одно обычное, а другое «повышенного» разрешения? Да и вообще, зачем здесь definы? Не лучше ли было бы этот выбор делать через шаблонный параметр, аргумент функции или просто через имя функции? Также было бы интересно увидеть сравнение производительности с другими аналогичными библиотеками, помимо stl.
    Вот, например: www.pcg-random.org


  1. Sdima1357
    02.11.2017 15:10
    #10503460

    Вот Вам пример на базе этой библиотеки(Обратите внимание на два последних случая): 

    	const int Cycles = 100000000;
        FRand  fr;
	FRand  fr1;
	{
		HiCl cl("gen");
		summ=0;
		for (int k=0;k<Cycles;k++)
		{
			summ+=fr.urand();
		}
	}
	cout<<summ/Cycles<<"\n";;
	{
		HiCl cl("gen");
		summ = 0;
		summ1 = 0;
		for (int k=0;k<Cycles/2;k++)
		{
			summ+=fr.urand();
			summ1+=fr.urand();
		}
	}
	cout<<(summ+summ1)/Cycles<<"\n";
	
	{
		HiCl cl("gen");
		summ=0;
		summ1 = 0;
		for (int k=0;k<Cycles/2;k++)
		{
			summ+=fr.urand();
			summ1+=fr1.urand();
		}
	}
	cout<<(summ+summ1)/Cycles<<"\n";

    //log
    gen 351.955 ms
    0.499969
    gen 347.921 ms
    0.500026
    gen 272.77 ms
    0.499971

    Собственно оболочка:
    #ifndef FRand_H
#define FRand_H
extern "C"
{
#include <tinymt32.h>
}
class FRand
{
	tinymt32_t tinymt;
public:	
	FRand()
	{
                tinymt.mat1 = 0x8f7011ee;
	        tinymt.mat2 = 0xfc78ff1f;
	        tinymt.tmat = 0x3793fdff;
		int seed = 1;
		tinymt32_init(&tinymt, seed);
	}
	FRand(int seed)
	{
                tinymt.mat1 = 0x8f7011ee;
	        tinymt.mat2 = 0xfc78ff1f;
	        tinymt.tmat = 0x3793fdff;
		tinymt32_init(&tinymt, seed);
	}
	inline double urand()
	{
		return tinymt32_generate_32double(&tinymt);	
	}
	uint32_t 	rand()
	{
		return tinymt32_generate_uint32(&tinymt);
	}
};
#endif


    1. The_Freeman Автор
      02.11.2017 15:37
      #10503508

      Если мы работаем в одном потоке, нужно ли нам создавать несколько экземпляров FRand? Я исходил из того, что нет, и поэтому генератор был статическим. Иначе, для разных экземпляров может возникать проблема коллизии. Или я не прав?


      1. Sdima1357
        02.11.2017 15:46
        #10503522

        Вот именно для отсутствия коллизий и нужно Ваши статические переменные переложить в members, как в моем примере. Компилятор использует больше регистров и уменьшает latency. посмотрите разницу между 2 и 3 примером по скорости


        1. The_Freeman Автор
          02.11.2017 15:54
          #10503534

          Возможно, у нас путаница в терминологии. Под коллизией я подразумевал совпадения значений seed у двух экземпляров. В Вашем примере они и так равны по умолчанию. Но две одинаковые выборки нам не нужны.


          1. Sdima1357
            02.11.2017 15:58
            #10503536

            Они сдвинуты.:) На Cycles*2.
            Инициализируйте разными seed из того же time


            1. The_Freeman Автор
              02.11.2017 16:11
              #10503552

              А если у меня не два, а несколько десятков экземпляров FRand? Мне для каждого seed запоминать?

              P.s. Если использовать только time, то seedы тоже будут одинаковыми, если созданы в одно время.


              1. Sdima1357
                02.11.2017 16:22
                #10503564

                Больше 2 в одном потоке выигрыша по скорости скорее всего не дадут.
                А зачем Вам 10? Первый рандом инит из time остальные из первого:
                FRand fr(time_count());
                FRand fr1(fr.rand());
                FRand fr2(fr.rand());


  1. Psychopompe
    02.11.2017 22:58
    #10504082

    А как она по сравнению с генераторами GSL?