Наборами данных в миллионы экземпляров в задачах машинного обучения уже давным давно никого не удивишь. Однако мало кто задаётся вопросом, как качественно визуализировать эти титанические пласты информации. Когда размер датасета превышает миллион, становится довольно грустно использовать стандартный t-SNE; остаётся играться с даунсэмплированием или вовсе ограничиваться грубыми статистическими инструментами. Но на каждую задачу найдётся свой инструмент. В своей статье я бы хотел рассмотреть два алгоритма, которые преодолевают барьер квадратичной сложности: уже хорошо известный Barnes-Hut t-SNE и новый претендент на звание «золотого молотка infovis'a» LargeVis.

(Это не картина художника-абстракциониста, а визуализация LiveJournal-датасета с высоты птичьего полёта)
Хоть t-SNE от силы лет десять, можно без опаски сказать, что он уже апробирован временем. Он пользуется популярностью не только среди матёрых адептов науки о данных, но и среди авторов научно-популярных статей. Про него уже писали на Хабре; также про этот алгоритм визуализации есть много хороших статей на просторах интернета.
Однако почти все эти статьи рассказывают про стандартный t-SNE. Напомню его вкратце:
Где — дивергенция Кульбака-Лейблера.
Интуитивно для трёхмерного случая это можно представить следующим образом. У вас есть бильярдных шаров. Вы маркируете их и подвешиваете их за нитки к потолку. Нитки разного размера, так что теперь в трёхмерном пространстве вашей комнаты висит датасет из элементов с . Вы соединяете каждую пару шаров идеальной пружиной так, что пружины ровно той длины, которой нужно (не провисают, но и не натянуты). Жёсткость пружин выбираются следующим образом: если рядом с некоторым шаром шаром нет других шаров, все пружины более-менее слабые. Если ровно один шар-сосед, а все остальные далеко, то до этого соседа будет очень жёсткая пружина, а до всех остальных — слабые. Если два соседа, до соседей будут жёсткие пружины (но слабее, чем в предыдущем случае), а до всех остальных — ещё слабее. И так далее.
Теперь вы берёте получившуюся конструкцию и пытаетесь разместить её на столе. Даже если трёхмерный объект состоит из свободно двигающихся узлов, в общем случае его нельзя разместить на плоскости (представьте, как вы прижимаете к столу тетраэдр), так что вы просто располагаете его так, чтобы натяжение или растяжение пружин было как можно меньше. Не забываем сделать поправку на то, что в двумерном пространстве у каждого шара будет меньше ближних соседей, но больше соседей на среднем расстоянии (помним про закон куба-квадрата). Большинство пружин настолько слабые, что их можно вовсе не брать в расчёт, но элементы, связанные сильными пружинами лучше расположить рядом. Вы двигаетесь маленькими шажками, двигаясь от произвольной начальной конфигурации, потихоньку уменьшая натяжение пружин. Чем качественнее вы можете восстановить исходное натяжение пружин по их текущему натяжению, тем лучше.
(забыли на секунду, что мы знаем, что изначальное натяжение пружин равно нулю)
(я упоминал, что это волшебные шары и пружины, которые проходят друг сквозь друга?)
(зачем вообще заниматься такой ерундой? — оставлено, как упражнение читателю)
Так вот, современные data science пакеты реализуют не совсем это. Стандартный t-SNE обладает сложностью . В результате последних исследований, оказалось, что это избыточно, и почти такого же результата можно достичь за операций.
Во-первых, считать на первом шаге все кажется явно избыточным. Большая их часть всё равно будет равна нулю. Ограничим это число: найдём k ближайших соседей каждого экземпляра данных, и посчитаем по-честному только для них; для остальных положим нулю. Соответственно, и сумму в знаменателе соответствующей формулы будем считать только по этим элементам. Встаёт вопрос: как именно выбрать это число соседей? Ответ на него на удивление прост: у нас уже есть параметр, ответственный за соотношение между глобальной и локальной структурой алгоритма — , perplexity! Его характерные значения лежат в диапазоне от 5 до 50, причём, чем больше датасет, тем больше perplexity. Как раз то что надо. При помощи VP-дерева можно найти достаточное количество соседей за времени. Если продолжать аналогию с пружинками, это как соединять не все шары попарно, а для каждого шара вешать пружины до, скажем, его пяти ближайших соседей.
Во-вторых…
Отвлечёмся немного, чтобы обсудить Barnes-Hut. Про этот алгоритм не было отдельной статьи на Хабре, а тут как раз отличный повод рассказать про него.
Наверное, каждому знакома классическая гравитационная задача N тел: по заданным массам и начальным координатам N космических тел и известному закону их взаимодействия построить функции, показывающие координаты объектов во все последующие моменты времени. Её решение не выражается через привычные нам алгебраические функции, а может быть лишь найдено численно, например, при помощи метода Рунге-Кутты. К сожалению, подобные численные методы решения дифференциальных уравнений имеют сложность , и даже на современных компьютерах не очень хорошо считаются, когда количество объектов превышает .
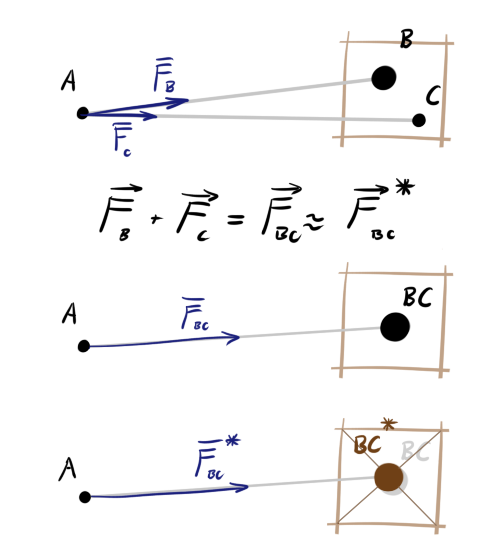
Для симуляций с таким громадным числом тел приходится идти на некоторые упрощения. Заметим, что для тройки тел A, B и C сумма сил действующих на A со стороны B и C равна силе, которую бы оказывало единое тело (BC), помещённое в точку центра масс B и C. Одного этого для оптимизации мало, поэтому применим ещё одну хитрость. Разобьём пространство на клетки. Если расстояние от тела A до клетки велико и в клетке больше одно тела, будем считать, что ровно в центре этой клетки помещён объект с суммарной массой объектов внутри. Его положение будет немного отклоняться от настоящего центра масс содержимого клетки, но чем дальше клетка, тем более незначительным будет ошибка в угле действия силы.
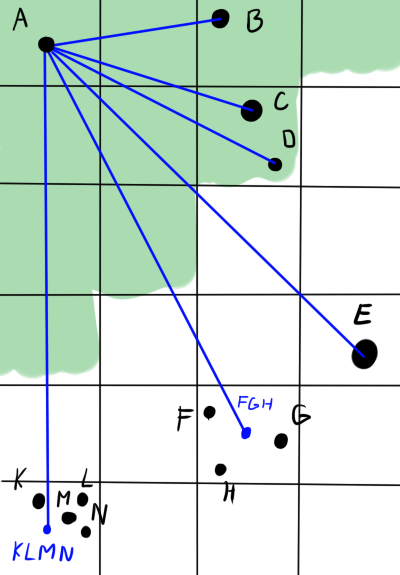
На картинке ниже зелёным обозначена область близости тела A. Синим обозначены направления действия сил. Тела B, C и D оказывают силу на A по-отдельности. Хоть С и D находятся в одной клетке, они в области точности. E тоже оказывает силу в одиночку — оно одно в клетке. А вот объекты F, G и H достаточно далеко от A и достаточно близко друг к другу, что взаимодействие можно приблизить. Центр клетки не всегда будет хорошо совпадать с реальным положением центра тяжести (см. K, L, M, N), но в среднем, при большом расстоянии и большом количестве тел, ошибка будет пренебрежимо мала.
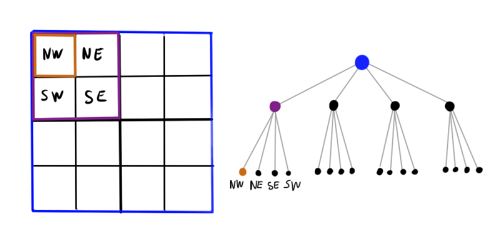
Стало лучше: мы уменьшили эффективное число объектов в несколько раз. Но как же выбрать оптимальный размер разбиения? Если разбиение будет слишком мелким, толку от него не будет, а если слишком большим, увеличится ошибка и придётся поставить очень большое расстояние, на котором мы будем готовы пожертвовать точностью. Сделаем ещё шаг вперёд: вместо сетки с фиксированным шагом разобьём прямоугольник плоскости на иерархию клеток. Крупные клетки содержат в себе мелкие, те ещё более мелкие и так далее. Получившаяся структура данных является деревом, где каждая нелистовая нода, порождает четыре дочерних ноды. Такая конструкция называется «квадродерево» (quadtree). Для трёхмерного случая, соответственно, используется октодерево (octotree). Теперь при рассчёте силы, действующей на некоторое тело, можно обходить дерево до тех пор пока не встретится клетка с достаточным уровнем мелкости, после чего использовать приближение.
Ноды, в которые не попадает ни одного объекта нет смысла мельчить дальше, поэтому эта структура не такая тяжеловесная, как может показаться на первый взгляд. С другой стороны, накладные расходы определённо есть, так что я бы сказал, что пока симулируемых объектов меньше сотни, такая хитрая структура данных может и немного вредить (зависит от реализации).
Теперь более формально:
Алгоритм 1:
Пусть — расстояние от тела до центра рассматриваемой клетки, — сторона этой клетки, — заранее заданный порог мелкости. Чтобы определить силу, оказываемую на объект , обходим квадродерево, начиная с корня.
Здесь более подробное выполнение алгоритма по шагам. Красивая анимация Barnes-Hut симуляции галактики. Различные реализации Barnes-Hut можно найти на гитхабе.
Очевидно, что такая интересная идея не могла остаться незамеченной и в других областях науки. Barnes-Hut применяют, везде, где встречаются системы с большим количеством объектов, каждый из которых действует на другие по простому закону, несильно меняющемуся в пространстве: симуляция роя, компьютерные игры. Вот и анализ данных тоже не оказался исключением. Распишем подробнее этап градиентного спуска (3) в t-SNE:
Где обозначены притягивающие силы, — отталкивающие, а — нормирующий множитель. Благодаря предыдущий оптимизации считается за , но — пока ещё . Вот тут нам и пригодится описанный выше трюк с квадродеревом и Barens-Hut, только вместо закона Ньютона у нас . Подобное упрощение и позволяет посчитать за в среднем. Недостаток очевиден: ошибки из-за дискретизации пространства. Laurens van der Maaten в статье выше утверждает, что пока даже не ясно, ограничены ли они вообще (приводятся ссылки на релевантные статьи). Как бы то ни было, результаты полученные при помощи Barens-Hut t-SNE с нормально подобранным выглядят состоятельно и последовательно. Обычно можно поставить или и забыть про него.
Можно ли ещё быстрее? Да. Зачем останавливаться на приближении «точка-клетка», когда можно упростить ситуацию ещё больше: если две клетки достаточно далеко друг от друга, можно приблизить не только конечный , но и начальный (приближение «клетка-клетка»). Это называется dual-tree algorithm (русского названия пока что нет). Мы не запускаем рекурсию выше для каждого экземпляра данных, а начинаем обходить квадродерево и когда мелкость достигает нужного значения начинаем обходить то же квадродерево и прикладываем к каждому экземпляру внутри выбранной клетки первого обхода суммарную силу из клетки второго обхода. Такой подход позволяет выжать ещё немного скорости, но ошибка начинает накапливаться намного быстрее, и приходится ставить меньший . Да и реализован такой обход не так много где.
Хорошо, но можно ли ещё быстрее? Jian Tang и компания, отвечают, что да!
Раз мы уже принесли в жертву точность, почему бы не принести в жертву ещё идевственницу детерминированность. Будем использовать случайные алгоритмы, чтобы получить результат за времени. Во-первых, вместо поиска ближайших соседей при помощи vantage point дерева, используем деревья случайных проекций (random projection trees, RT-деревья). Во-вторых, вместо честного подсчёта градиента с упрощениями через Barnes-Hut, будем просто-напросто сэмплирвать слагаемые в отрицательной части .
Идея с разбиением плоскости при помощи квадродерева была неплоха. Теперь попробуем разбить плоскость на сектора при помощи чего-нибудь более простого. Как насчёт k-d дерева?
Алгоритм 2:
Параметры: — минимальный размер, — набор данных
MakeTree()
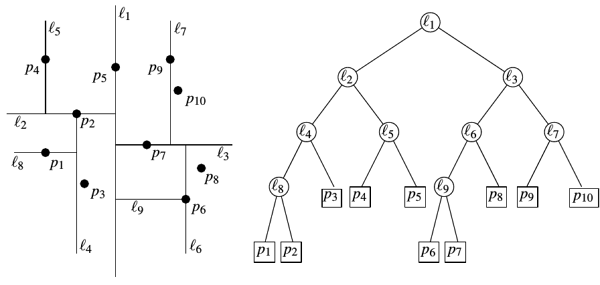
Как-то слишком примитивно. Перпендикулярность плоскости разбиения какой-то оси координат смотрится подозрительно. Есть более продвинутая версия: деревья случайных проекций (random projection trees, RT-деревья). Будем рекурсивно разбивать пространство, каждый раз выбирая случайный единичный вектор, перпендикулярно которому будет идти плоскость. Для лёгкой асимметричности дерева также добавим небольшой шум к точке привязки плоскости.
Алгоритм 3:
ChooseRule(X) // Мета-функция, которая возвращает предикат, по которому мы будем разбивать пространство
MakeRPTree()
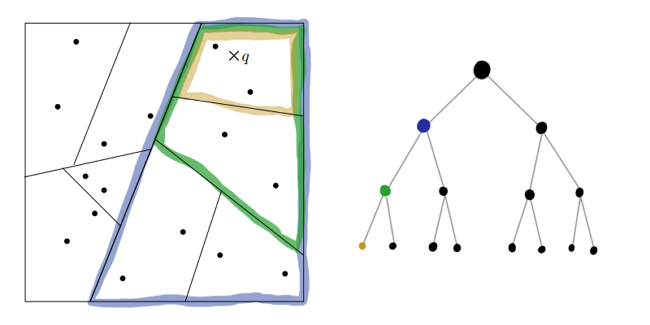
Неужели такое грубое и хаотичное разбиение способно дать хоть какие-то результаты? Оказывается, что да! В случае, когда многомерные данные на самом деле лежат вблизи не очень многомерной гиперскладки, RT-деревья ведут себя довольно-таки пристойно (см. доказательства по первой ссылке и здесь). Даже в случае, когда данные действительно имеют эффективную размерность сопоставимую с , знание о проекциях несёт немало информации.
Хм, сложность: посчитать медиану это всё же и мы делаем это на каждом из шагов. Упростим выбор гиперплоскости ещё больше: вообще откажемся от точки привязки. На каждом шаге рекурсии будем просто выбирать две случайные точки из очередного и проводить равноотстоящую от них плоскость.
Кажется, мы выбросили из алгоритма всё, что хоть как-то напоминает о математической строгости или точности. Как же получившиеся деревья могут помочь нам с поиском ближайших соседей? Очевидно, что соседи точки данных по листу графа — первые кандидаты в его kNN. Но это не точно: если точка лежит рядом с гиперплоскостью разбиения, настоящие соседи могут оказаться в совершенно другом листе. Получившееся приближение можно улучшить, если построить несколько RP-деревьев. Пересечение листов получившихся графов для каждого является гораздо лучшей областью для поиска.
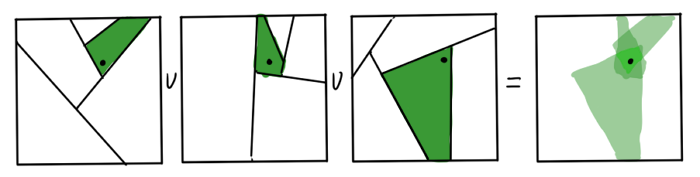
Деревьев не нужно слишком много, это подрывает быстродействие. Получившиеся приближение доводится до ума при помощи эвристики «сосед моего соседа — скорее всего мой сосед». Утверждается, что достаточно совсем немного итераций, чтобы получить приличный результат.
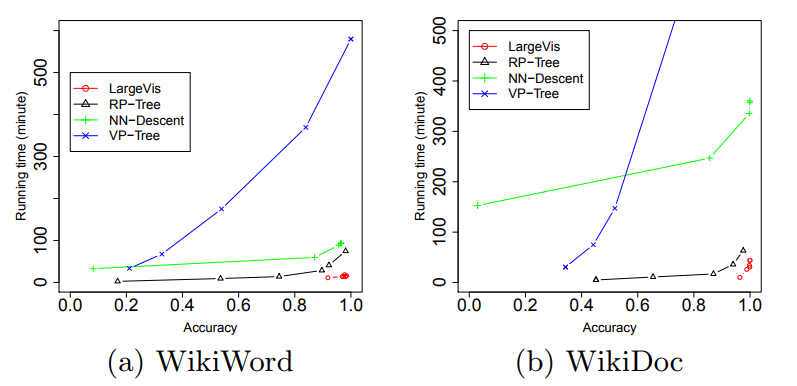
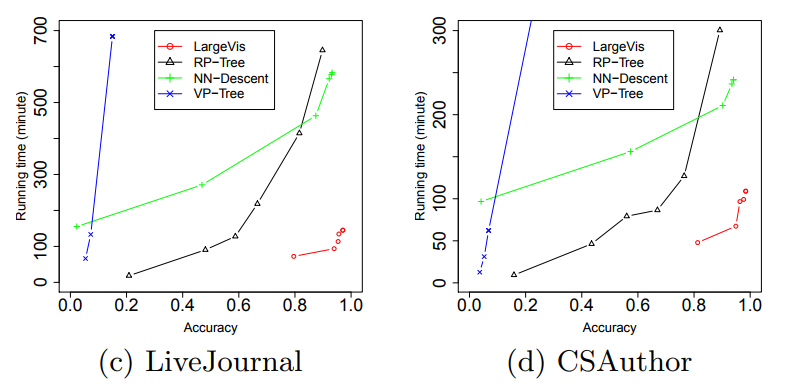
Авторы статьи уверяют, что эффективная реализация всего этого работает за времени. Есть, правда, одно но, которое они не упоминают: О-большое проглатывает гигантскую константу, на которую влияют , количество RP-деревьев, и количество этапов эвристической подстройки.
После вычисление kNN Jian Tang и КО считают подобие данных в исходном пространстве по такой же формуле, как и в t-SNE.
Обратите внимание, что сумма в знаменателе считается только по kNN, остальные равны 0; также .
После этого, предлагается хитрый теоретический манёвр: теперь мы смотрим на полученные , как на веса рёбер некоторого графа, где нодами являются элементы . Закодируем информацию о весах этого графа при помощи набора в пространстве отображения. Пусть вероятность наблюдать бинарное невзвешенное ребро равна
Снова используется t-распределение, только немного по-другому; всё ещё помним про разное количество соседей в разных слоях в пространствах с разным . Вероятность, что в исходном графе было ребро с весом в :
Перемножим вероятности для всех рёбер и получим расположение методом максимального правдоподобия:
Где — множество всех пар, которые не попали в список ближайших соседей, а — гиперпараметр, показывающий влияние несуществующих рёбер. Логарифмируем:
Снова получили сумму состоящую из двух частей: одна притягивает друг к другу близких друг к другу , другая отталкивает , которых не были соседями друг друга, только выглядят они по-другому. Также снова получили проблему, что точное вычисление второй подсуммы займёт , так как отсутствующих дуг в нашем графе огромное количество. На сей раз вместо использования квадродерева, предлагается сэмплировать узлы графа, до которых нет дуг. Этот приём пришёл из машинной обработки текстов. Там для более быстрого усвоения контекста для каждого слова , которое стоит в тексте рядом со словом , берут не все слова из словаря, которые рядом с не встречаются, а лишь несколько произвольных слов, с вероятностью пропорциональной 3/4 степени их частоты (показатель 3/4 подобран эмпирически, подробнее здесь). Мы же для каждой ноды , до которой есть ребро из с весом в , будем сэмплировать несколько произвольных нод, до которых рёбер нет, пропорционально 3/4 степени количества дуг, исходящих из тех нод.
Где — количество отрицательных рёбер на ноду, а .
Так как могут варьироваться в довольно широких пределах, для стабилизации градиента следует применить продвинутую версию техники сэмплирования. Вместо перебирания с одинаковой частотой, будем брать их вероятностью, пропорциональной и притворяться, что ребро единичное.
Ух. Что же дают нам все эти ухищрения? Примерно пятикратный прирост скорости на в меру больших датасетах по сравнению с Barnes-Hut t-SNE!

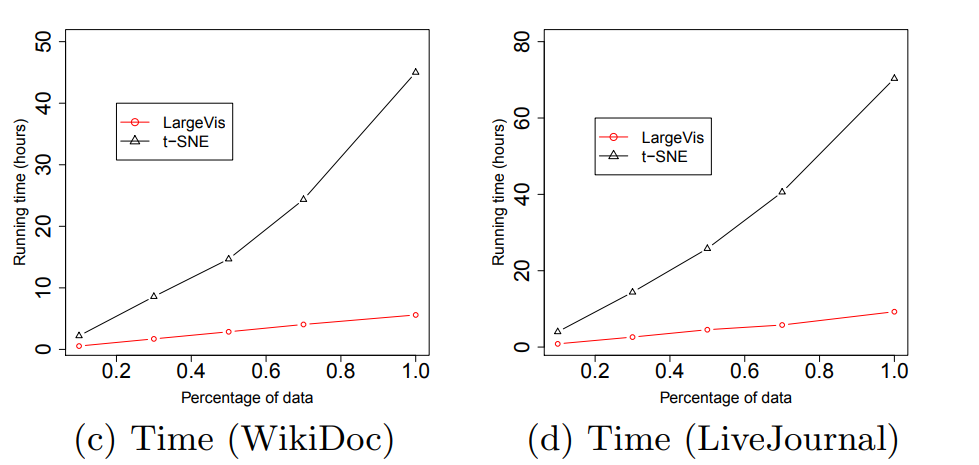
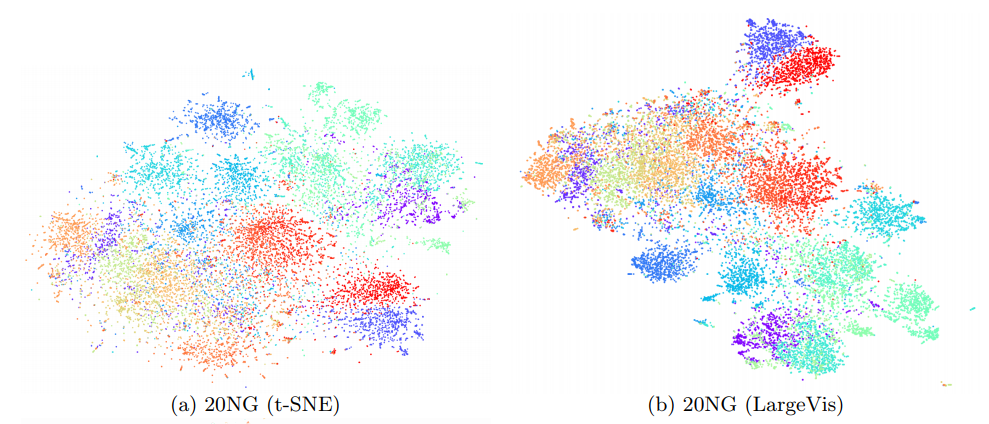


(Картинки взяты из статьи)
При этом качество визуализации примерно такое же. Внимательный читатель заметит, что на сравнительно маленьком датасете 20 Newsgroups () LargeVis проигрывает t-SNE. Это и есть влияние коварной константы, которая осталась за кадром. Студенты, помните, бездумное использование алгоритмов с меньшей степенью под О-большим вредит вашему здоровью!
Напоследок, пара практических моментов. Существует официальная имплементация LargeVis, но на мой взгляд код там слегка страшненький, используйте на свой страх и риск. Количество отрицательных сэмплов на ноду обычно берётся равным 5 (пришло из машинной обработки текстов). Эксперименты показали крайне незначительное увеличение качества при увеличении от 3 до 7. Количество деревьев следует брать тем больше, чем больше набор данных, но не слишком много. Ориентируйтесь на минимальное значение 10 для и близкое к избыточному 100 . создатели алгоритма берут равным 7, не объясняя, почему. Самое главное: LargeVis отлично параллелится на всех этапах работы. Благодаря разреженности матрицы весов асинхронный разреженный градиентный спуск на разных потоках вряд ли будет задевать друг друга.
Спасибо за внимание. Надеюсь, теперь вам стало понятнее, что это за таинственные method='barnes_hut' и angle в параметрах у sklearn'овского TSNE, и вы не потеряетесь, когда понадобится визуализировать датасет из десяти миллионов записей. Если вы работаете с большим количеством данных, может, вы найдёте собственное применение Barens-Hut или решитесь на внедрение LargeVis. На всякий случай, вот краткие заметки по работе последнего. Хорошего дня!


(Это не картина художника-абстракциониста, а визуализация LiveJournal-датасета с высоты птичьего полёта)
t-SNE с модификациями
Хоть t-SNE от силы лет десять, можно без опаски сказать, что он уже апробирован временем. Он пользуется популярностью не только среди матёрых адептов науки о данных, но и среди авторов научно-популярных статей. Про него уже писали на Хабре; также про этот алгоритм визуализации есть много хороших статей на просторах интернета.
Однако почти все эти статьи рассказывают про стандартный t-SNE. Напомню его вкратце:
- Посчитать для каждой пары пары точек данных их подобие друг другу в исходном пространстве с использованием Гауссова ядра:
- Для каждой пары точек отображения выразить их подобие в пространстве визуализации с использованием ядра t-распределения
- Построить целевую функцию и минимизировать её относительно при помощи градиентного спуска
Где — дивергенция Кульбака-Лейблера.
Интуитивно для трёхмерного случая это можно представить следующим образом. У вас есть бильярдных шаров. Вы маркируете их и подвешиваете их за нитки к потолку. Нитки разного размера, так что теперь в трёхмерном пространстве вашей комнаты висит датасет из элементов с . Вы соединяете каждую пару шаров идеальной пружиной так, что пружины ровно той длины, которой нужно (не провисают, но и не натянуты). Жёсткость пружин выбираются следующим образом: если рядом с некоторым шаром шаром нет других шаров, все пружины более-менее слабые. Если ровно один шар-сосед, а все остальные далеко, то до этого соседа будет очень жёсткая пружина, а до всех остальных — слабые. Если два соседа, до соседей будут жёсткие пружины (но слабее, чем в предыдущем случае), а до всех остальных — ещё слабее. И так далее.
Теперь вы берёте получившуюся конструкцию и пытаетесь разместить её на столе. Даже если трёхмерный объект состоит из свободно двигающихся узлов, в общем случае его нельзя разместить на плоскости (представьте, как вы прижимаете к столу тетраэдр), так что вы просто располагаете его так, чтобы натяжение или растяжение пружин было как можно меньше. Не забываем сделать поправку на то, что в двумерном пространстве у каждого шара будет меньше ближних соседей, но больше соседей на среднем расстоянии (помним про закон куба-квадрата). Большинство пружин настолько слабые, что их можно вовсе не брать в расчёт, но элементы, связанные сильными пружинами лучше расположить рядом. Вы двигаетесь маленькими шажками, двигаясь от произвольной начальной конфигурации, потихоньку уменьшая натяжение пружин. Чем качественнее вы можете восстановить исходное натяжение пружин по их текущему натяжению, тем лучше.
(забыли на секунду, что мы знаем, что изначальное натяжение пружин равно нулю)
(я упоминал, что это волшебные шары и пружины, которые проходят друг сквозь друга?)
(зачем вообще заниматься такой ерундой? — оставлено, как упражнение читателю)
Так вот, современные data science пакеты реализуют не совсем это. Стандартный t-SNE обладает сложностью . В результате последних исследований, оказалось, что это избыточно, и почти такого же результата можно достичь за операций.
Во-первых, считать на первом шаге все кажется явно избыточным. Большая их часть всё равно будет равна нулю. Ограничим это число: найдём k ближайших соседей каждого экземпляра данных, и посчитаем по-честному только для них; для остальных положим нулю. Соответственно, и сумму в знаменателе соответствующей формулы будем считать только по этим элементам. Встаёт вопрос: как именно выбрать это число соседей? Ответ на него на удивление прост: у нас уже есть параметр, ответственный за соотношение между глобальной и локальной структурой алгоритма — , perplexity! Его характерные значения лежат в диапазоне от 5 до 50, причём, чем больше датасет, тем больше perplexity. Как раз то что надо. При помощи VP-дерева можно найти достаточное количество соседей за времени. Если продолжать аналогию с пружинками, это как соединять не все шары попарно, а для каждого шара вешать пружины до, скажем, его пяти ближайших соседей.
Во-вторых…
Barnes-Hut алгоритм
Отвлечёмся немного, чтобы обсудить Barnes-Hut. Про этот алгоритм не было отдельной статьи на Хабре, а тут как раз отличный повод рассказать про него.
Наверное, каждому знакома классическая гравитационная задача N тел: по заданным массам и начальным координатам N космических тел и известному закону их взаимодействия построить функции, показывающие координаты объектов во все последующие моменты времени. Её решение не выражается через привычные нам алгебраические функции, а может быть лишь найдено численно, например, при помощи метода Рунге-Кутты. К сожалению, подобные численные методы решения дифференциальных уравнений имеют сложность , и даже на современных компьютерах не очень хорошо считаются, когда количество объектов превышает .
Для симуляций с таким громадным числом тел приходится идти на некоторые упрощения. Заметим, что для тройки тел A, B и C сумма сил действующих на A со стороны B и C равна силе, которую бы оказывало единое тело (BC), помещённое в точку центра масс B и C. Одного этого для оптимизации мало, поэтому применим ещё одну хитрость. Разобьём пространство на клетки. Если расстояние от тела A до клетки велико и в клетке больше одно тела, будем считать, что ровно в центре этой клетки помещён объект с суммарной массой объектов внутри. Его положение будет немного отклоняться от настоящего центра масс содержимого клетки, но чем дальше клетка, тем более незначительным будет ошибка в угле действия силы.

На картинке ниже зелёным обозначена область близости тела A. Синим обозначены направления действия сил. Тела B, C и D оказывают силу на A по-отдельности. Хоть С и D находятся в одной клетке, они в области точности. E тоже оказывает силу в одиночку — оно одно в клетке. А вот объекты F, G и H достаточно далеко от A и достаточно близко друг к другу, что взаимодействие можно приблизить. Центр клетки не всегда будет хорошо совпадать с реальным положением центра тяжести (см. K, L, M, N), но в среднем, при большом расстоянии и большом количестве тел, ошибка будет пренебрежимо мала.

Стало лучше: мы уменьшили эффективное число объектов в несколько раз. Но как же выбрать оптимальный размер разбиения? Если разбиение будет слишком мелким, толку от него не будет, а если слишком большим, увеличится ошибка и придётся поставить очень большое расстояние, на котором мы будем готовы пожертвовать точностью. Сделаем ещё шаг вперёд: вместо сетки с фиксированным шагом разобьём прямоугольник плоскости на иерархию клеток. Крупные клетки содержат в себе мелкие, те ещё более мелкие и так далее. Получившаяся структура данных является деревом, где каждая нелистовая нода, порождает четыре дочерних ноды. Такая конструкция называется «квадродерево» (quadtree). Для трёхмерного случая, соответственно, используется октодерево (octotree). Теперь при рассчёте силы, действующей на некоторое тело, можно обходить дерево до тех пор пока не встретится клетка с достаточным уровнем мелкости, после чего использовать приближение.

Ноды, в которые не попадает ни одного объекта нет смысла мельчить дальше, поэтому эта структура не такая тяжеловесная, как может показаться на первый взгляд. С другой стороны, накладные расходы определённо есть, так что я бы сказал, что пока симулируемых объектов меньше сотни, такая хитрая структура данных может и немного вредить (зависит от реализации).
Теперь более формально:
Алгоритм 1:
Пусть — расстояние от тела до центра рассматриваемой клетки, — сторона этой клетки, — заранее заданный порог мелкости. Чтобы определить силу, оказываемую на объект , обходим квадродерево, начиная с корня.
- Если в текущей клетке нет ни одного элемента, пропускаем её
- Иначе, если в ноде только один элемент и это не , напрямую добавляем его влияение к суммарной силе
- Иначе, если , считаем эту ноду единым целым объектом, и прибавляем его суммарную силу, как описано выше
- Иначе рекурсивно запускаем эту процедуру для всех дочерних клеток текущей клетки
Здесь более подробное выполнение алгоритма по шагам. Красивая анимация Barnes-Hut симуляции галактики. Различные реализации Barnes-Hut можно найти на гитхабе.
Очевидно, что такая интересная идея не могла остаться незамеченной и в других областях науки. Barnes-Hut применяют, везде, где встречаются системы с большим количеством объектов, каждый из которых действует на другие по простому закону, несильно меняющемуся в пространстве: симуляция роя, компьютерные игры. Вот и анализ данных тоже не оказался исключением. Распишем подробнее этап градиентного спуска (3) в t-SNE:
Где обозначены притягивающие силы, — отталкивающие, а — нормирующий множитель. Благодаря предыдущий оптимизации считается за , но — пока ещё . Вот тут нам и пригодится описанный выше трюк с квадродеревом и Barens-Hut, только вместо закона Ньютона у нас . Подобное упрощение и позволяет посчитать за в среднем. Недостаток очевиден: ошибки из-за дискретизации пространства. Laurens van der Maaten в статье выше утверждает, что пока даже не ясно, ограничены ли они вообще (приводятся ссылки на релевантные статьи). Как бы то ни было, результаты полученные при помощи Barens-Hut t-SNE с нормально подобранным выглядят состоятельно и последовательно. Обычно можно поставить или и забыть про него.
Можно ли ещё быстрее? Да. Зачем останавливаться на приближении «точка-клетка», когда можно упростить ситуацию ещё больше: если две клетки достаточно далеко друг от друга, можно приблизить не только конечный , но и начальный (приближение «клетка-клетка»). Это называется dual-tree algorithm (русского названия пока что нет). Мы не запускаем рекурсию выше для каждого экземпляра данных, а начинаем обходить квадродерево и когда мелкость достигает нужного значения начинаем обходить то же квадродерево и прикладываем к каждому экземпляру внутри выбранной клетки первого обхода суммарную силу из клетки второго обхода. Такой подход позволяет выжать ещё немного скорости, но ошибка начинает накапливаться намного быстрее, и приходится ставить меньший . Да и реализован такой обход не так много где.
LargeVis
Хорошо, но можно ли ещё быстрее? Jian Tang и компания, отвечают, что да!
Раз мы уже принесли в жертву точность, почему бы не принести в жертву ещё и
RT-деревья
Идея с разбиением плоскости при помощи квадродерева была неплоха. Теперь попробуем разбить плоскость на сектора при помощи чего-нибудь более простого. Как насчёт k-d дерева?
Алгоритм 2:
Параметры: — минимальный размер, — набор данных
MakeTree()
- Если вернуть текущий , как листовую ноду
- Иначе
- Выбрать случайным образом номер переменной
- Rule(x) := median() // Предикат разбивающий подпространство данных гиперплоскостью, перпендикулярной оси координат и проходящей через медиану значений -той переменной элементов .
- LeftTree := MakeTree({x X: Rule(x) = true})
- RightTree := MakeTree({x X: Rule(x) = false})
- Вернуть [Rule, LeftTree, RightTree]

Как-то слишком примитивно. Перпендикулярность плоскости разбиения какой-то оси координат смотрится подозрительно. Есть более продвинутая версия: деревья случайных проекций (random projection trees, RT-деревья). Будем рекурсивно разбивать пространство, каждый раз выбирая случайный единичный вектор, перпендикулярно которому будет идти плоскость. Для лёгкой асимметричности дерева также добавим небольшой шум к точке привязки плоскости.
Алгоритм 3:
ChooseRule(X) // Мета-функция, которая возвращает предикат, по которому мы будем разбивать пространство
- Выбрать случайный единичный вектор из
- Выбрать случайный
- Пусть — самая далёкая от него точка данных в
- := случайное число в
- Вернуть Rule(x) := (median() + )
MakeRPTree()
- Если вернуть текущий , как листовую ноду
- Иначе
- Rule(x) := ChooseRule(X)
- LeftTree := MakeTree({x X: Rule(x) = true})
- RightTree := MakeTree({x X: Rule(x) = false})
- Вернуть [Rule, LeftTree, RightTree]

Неужели такое грубое и хаотичное разбиение способно дать хоть какие-то результаты? Оказывается, что да! В случае, когда многомерные данные на самом деле лежат вблизи не очень многомерной гиперскладки, RT-деревья ведут себя довольно-таки пристойно (см. доказательства по первой ссылке и здесь). Даже в случае, когда данные действительно имеют эффективную размерность сопоставимую с , знание о проекциях несёт немало информации.
Хм, сложность: посчитать медиану это всё же и мы делаем это на каждом из шагов. Упростим выбор гиперплоскости ещё больше: вообще откажемся от точки привязки. На каждом шаге рекурсии будем просто выбирать две случайные точки из очередного и проводить равноотстоящую от них плоскость.
Кажется, мы выбросили из алгоритма всё, что хоть как-то напоминает о математической строгости или точности. Как же получившиеся деревья могут помочь нам с поиском ближайших соседей? Очевидно, что соседи точки данных по листу графа — первые кандидаты в его kNN. Но это не точно: если точка лежит рядом с гиперплоскостью разбиения, настоящие соседи могут оказаться в совершенно другом листе. Получившееся приближение можно улучшить, если построить несколько RP-деревьев. Пересечение листов получившихся графов для каждого является гораздо лучшей областью для поиска.

Деревьев не нужно слишком много, это подрывает быстродействие. Получившиеся приближение доводится до ума при помощи эвристики «сосед моего соседа — скорее всего мой сосед». Утверждается, что достаточно совсем немного итераций, чтобы получить приличный результат.


Авторы статьи уверяют, что эффективная реализация всего этого работает за времени. Есть, правда, одно но, которое они не упоминают: О-большое проглатывает гигантскую константу, на которую влияют , количество RP-деревьев, и количество этапов эвристической подстройки.
Сэмплирование
После вычисление kNN Jian Tang и КО считают подобие данных в исходном пространстве по такой же формуле, как и в t-SNE.
Обратите внимание, что сумма в знаменателе считается только по kNN, остальные равны 0; также .
После этого, предлагается хитрый теоретический манёвр: теперь мы смотрим на полученные , как на веса рёбер некоторого графа, где нодами являются элементы . Закодируем информацию о весах этого графа при помощи набора в пространстве отображения. Пусть вероятность наблюдать бинарное невзвешенное ребро равна
Снова используется t-распределение, только немного по-другому; всё ещё помним про разное количество соседей в разных слоях в пространствах с разным . Вероятность, что в исходном графе было ребро с весом в :
Перемножим вероятности для всех рёбер и получим расположение методом максимального правдоподобия:
Где — множество всех пар, которые не попали в список ближайших соседей, а — гиперпараметр, показывающий влияние несуществующих рёбер. Логарифмируем:
Снова получили сумму состоящую из двух частей: одна притягивает друг к другу близких друг к другу , другая отталкивает , которых не были соседями друг друга, только выглядят они по-другому. Также снова получили проблему, что точное вычисление второй подсуммы займёт , так как отсутствующих дуг в нашем графе огромное количество. На сей раз вместо использования квадродерева, предлагается сэмплировать узлы графа, до которых нет дуг. Этот приём пришёл из машинной обработки текстов. Там для более быстрого усвоения контекста для каждого слова , которое стоит в тексте рядом со словом , берут не все слова из словаря, которые рядом с не встречаются, а лишь несколько произвольных слов, с вероятностью пропорциональной 3/4 степени их частоты (показатель 3/4 подобран эмпирически, подробнее здесь). Мы же для каждой ноды , до которой есть ребро из с весом в , будем сэмплировать несколько произвольных нод, до которых рёбер нет, пропорционально 3/4 степени количества дуг, исходящих из тех нод.
Где — количество отрицательных рёбер на ноду, а .
Так как могут варьироваться в довольно широких пределах, для стабилизации градиента следует применить продвинутую версию техники сэмплирования. Вместо перебирания с одинаковой частотой, будем брать их вероятностью, пропорциональной и притворяться, что ребро единичное.
Ух. Что же дают нам все эти ухищрения? Примерно пятикратный прирост скорости на в меру больших датасетах по сравнению с Barnes-Hut t-SNE!





(Картинки взяты из статьи)
При этом качество визуализации примерно такое же. Внимательный читатель заметит, что на сравнительно маленьком датасете 20 Newsgroups () LargeVis проигрывает t-SNE. Это и есть влияние коварной константы, которая осталась за кадром. Студенты, помните, бездумное использование алгоритмов с меньшей степенью под О-большим вредит вашему здоровью!
Напоследок, пара практических моментов. Существует официальная имплементация LargeVis, но на мой взгляд код там слегка страшненький, используйте на свой страх и риск. Количество отрицательных сэмплов на ноду обычно берётся равным 5 (пришло из машинной обработки текстов). Эксперименты показали крайне незначительное увеличение качества при увеличении от 3 до 7. Количество деревьев следует брать тем больше, чем больше набор данных, но не слишком много. Ориентируйтесь на минимальное значение 10 для и близкое к избыточному 100 . создатели алгоритма берут равным 7, не объясняя, почему. Самое главное: LargeVis отлично параллелится на всех этапах работы. Благодаря разреженности матрицы весов асинхронный разреженный градиентный спуск на разных потоках вряд ли будет задевать друг друга.
Заключение
Спасибо за внимание. Надеюсь, теперь вам стало понятнее, что это за таинственные method='barnes_hut' и angle в параметрах у sklearn'овского TSNE, и вы не потеряетесь, когда понадобится визуализировать датасет из десяти миллионов записей. Если вы работаете с большим количеством данных, может, вы найдёте собственное применение Barens-Hut или решитесь на внедрение LargeVis. На всякий случай, вот краткие заметки по работе последнего. Хорошего дня!

Комментарии (2)

VladVin
06.11.2017 00:11Отличная статья. Отдельное спасибо за разжеванную математику и алгоритмы. До этого использовал t-SNE, теперь кругозор расширился, буду знать о LargeVis


vesper-bot
Большое спасибо за октодерево :) Да и вообще очень понравилось.