Памятуя о том, что на Хабрахабр заглядывают люди разной математической подготовки, — однако, в поле интересов которых вполне может попадать тема линейных преобразований, — в связи с её практической значимостью, — я попробую рассказать об этом максимально доступно.
Продолжим историю

Треугольные очертания лодки, шляпы и удочки над водой настолько поразили философа-математика, что он застыл как заворожённый.
Удочка рыбака аккуратно зависла над гладью вод Жёлтой Реки под углом, равным 45 градусам.
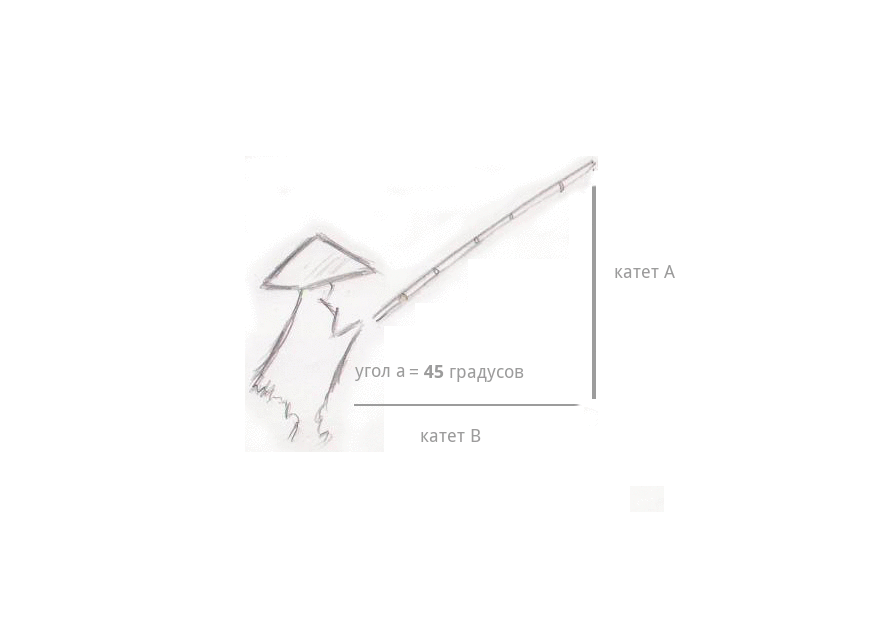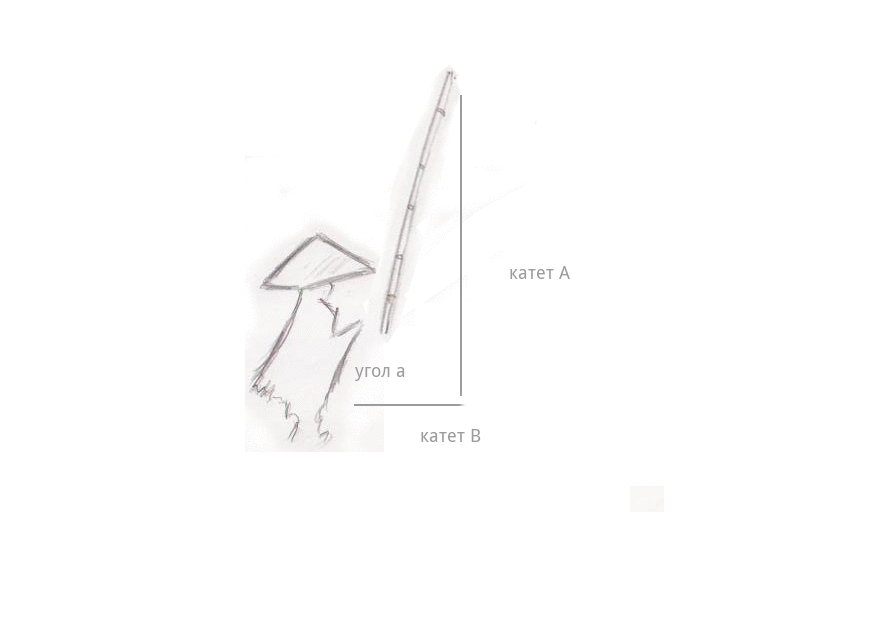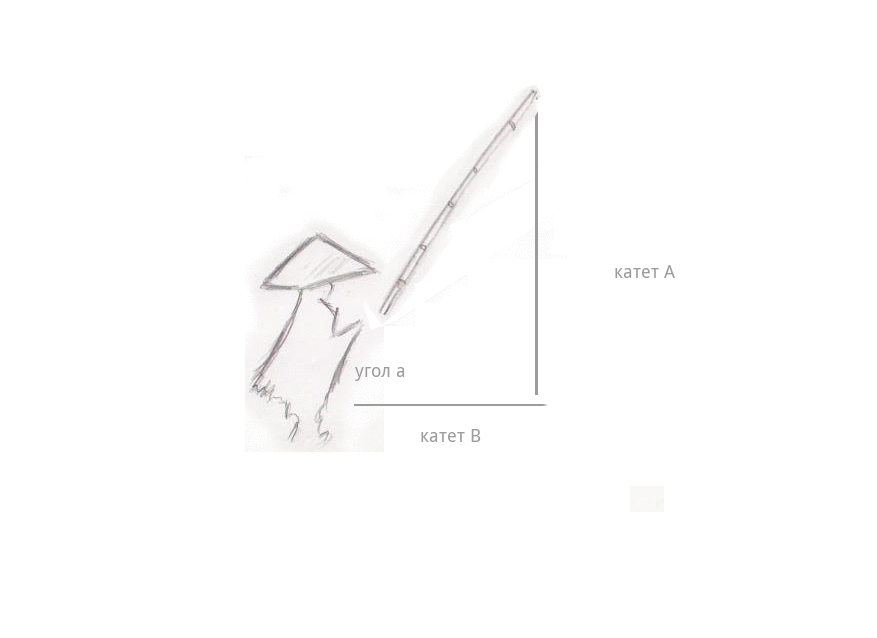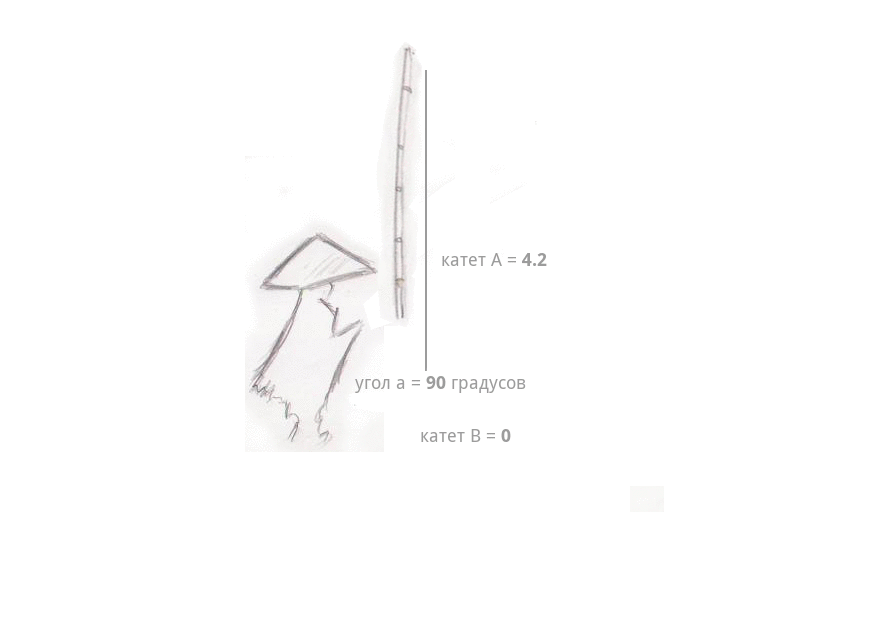
Лёгкий туман стелился над водой… и вдруг — поклёв. Рыбак потянул удочку, и она стала быстро набирать высоту, длина лески (катет А) стала расти на глазах, а расстояние от рыбака до самой лески стало уменьшаться (катет B). И самое интересное — длина самой удочки совсем не изменилась — телескопических удочек ещё не было, — даже когда она описала в воздухе дугу и оказалась почти над головой рыбака, под углом 90 градусов. Длина лески сравнялась с длиной удочки — катушки тогда уже были, — а расстояние между рыбаком и леской изменилось до 0, леска оказалась в руках рыбака.
Последний момент очень важен для понимания того, что происходит при умножении вектора-удочки на матрицу поворота.
Ностальгируем и думаем дальше...
Вспомним теорему Пифагора: квадрат длины удочки равен сумме квадратов катетов — самой лески и расстоянию между рыбаком и тем местом, где леска погружена в воду — С^2=А в квадрате + B в квадрате.
Представим, что длина удочки 4.2, длина (или высота над водой) лески 3, расстояние между рыбаком и местом, где леска погружена в воду тоже 3.
Окунёмся в поиски
1) найдём то, как соотносится между собой длина лески с длиной удочки — синус угла а.
2) найдём то, как соотносится длина отрезка между рыбаком и местом погружения лески с длиной удочки — косинус а. Считаем:
sin(a) = 3/ 4.2= 0.7
cos(a) = 3/ 4.2 = 0.7
А теперь порассуждаем
Что будет если катет А разделить на sin(a)?! т.е.:
3/0.7= 4.2
Получаем длину удочки — гипотенузу.
А если мы умножим катет А на sin(а)?!
3*0.7= 2.1
Отметим это расстояние на гипотенузе — 2.1.
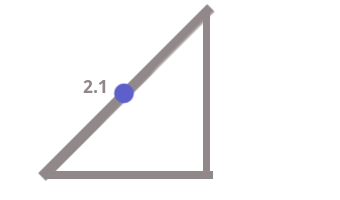
На оставшееся расстояние также приходится — 2.1, так как очевидно:
4.2-2.1=2.1
Это означает, то как в текущий момент времени синус и косинус делят гипотенузу. Поскольку квадрат гипотенузы это 4.2*4.2, то вопрос: что будет если 4.2 умножить на 2.1?! На ту самую её часть, с которой связан один из катетов:
4.2*2.1 = 9, (корень: 3)
Тоже самое для второго катета.
Нашли катеты. И убедились в том, что со времён Пифагора ничего не изменилось.
Далее
Теперь ещё раз осуществим умножение катета А на sin(a), катета B на cos(a).
3*0.7= 2,1
3*0.7 = 2,1
Суммируем:
2.1 + 2.1 =4.2
или
3*0.7 + 3*0.7 =4.2
Снова получили число равное длине удочки… и мы вплотную подобрались к матрице поворота.
Напомню формулу

(изображение из Википедии. Ссылка на статью)
Возьмём её нижнюю часть — получение точки y:
y=x*sin(Ф)+y*cos(Ф)
И сравним с вычислениями выше:
3*0.7 + 3*0.7 = 4.2
y=x*sin(Ф)+y*cos(Ф)
Как две капли воды. Y в нашем случае окажется равным 4.2.
Если применить первую часть формулы к вычислениям, то получим:
3*0.7 — 3*0.7 = 0
Иными словами случится так:
x станет 0 — рыбак поймает леску.
y станет 4.2 — леска сравняется с длиной удочки.
Помним, что для вычисления x синус и косинус меняются местами.
Ф в данном случае равно 45 градусам (Ф = 0.7 ) и при таком угле синус и косинус равны, что удобно для примера. В остальных случаях очевидно величины для синуса и косинуса будут другие. Например, для 40 градусов: cosdegree(40) = 0,7660444431, sindegree(40) = 0,6427876097 (если вы не согласны, обращайтесь в Яндекс, я пользовался его калькулятором).
В итоге
Применяя формулу к новым значениям x,y несколько раз — в цикле, наглядно увидим движение по окружности, каждый раз на 45 градусов.
Если требуется сдвинуть вектор-удочку на один градус, то его и подставляем в формулу на место Ф.
Как происходит вычисление тригонометрических функций?!
Как известно, для вычисления косинуса и синуса угла обычно используются готовые функции. Согласно информации по ссылке вычисление и точность зависят от системы. Для unix-систем есть по крайней мере два варианта: функция, написанная в недрах компании IBM и встроенная инструкция fsin на Ассемблере. Есть также библиотека fdlibm с достаточно наглядным кодом и комментариями, по которым видно, что синус и косинус вычисляются в этой библиотеке через число pi.
А вдруг автор этой статьи все придумал?
Если у вас на компьютере есть веб-сервер и интерпретатор языка PHP, то можно поэкспериментировать со следующим кодом, который вращает блок CSS div:
Файл index.php
<?php
if (isset($_GET['ok'])) {
$x= $_GET['x']*cos(1)-$y=$_GET['y']*sin(1);
$y= $_GET['x']*sin(1)+$y=$_GET['y']*cos(1);
}
?>
<style>
#rotation_martix {
position: absolute;
top: <?=$x+300?>px;
left: <?=$y+300?>px;
background-color: #999;
width: 10px;
height: 10px;
}
</style>
< div id="rotation_martix">
</ div>
<form method="GET" >
<input type="submit" name="ok" value="ok">
<input type="text" name="x" value="<?=$x?>">
<input type="text" name="y" value="<?=$y?>">
</form>
Если немного изменить матрицу, то можно получить вращение по спирали или сделать из точки маятник.
Комментарии (23)

SanQri
19.11.2017 13:28Почему в топе хабра математика первый курс без математики?
FadeToBlack
20.11.2017 07:51Для программистов же. Большинство программистов не умеют переваривать математику в первозданном, неадаптированном виде.

AllexIn
20.11.2017 21:35-1Умеют.
Просто, к сожалению, часто математику не дают по шагам, а дают «вот так, потому что...». И всё. В итоге матрицы знаешь, формулы знаешь, а как они выведены — нет.
dcc0 Автор
20.11.2017 23:41Случайно минус поставил. С телефона. И на нем стрелки смотрят в одну сторону.
В общем + в карму от меня тогда.

FadeToBlack
21.11.2017 08:10На мой практический взгляд программиста-самоучки и законченного троечника, с точки зрения традиционной системы образования, как выводятся формулы — интересно только небольшому количеству людей, которые способы воспринимать абстрактную информацию, «висящую в воздухе» (читай, математикам). Лично мне кажется, что должны быть примеры практического применения для каждой из формул, тогда все обретает смысл, легче усваивается и так далее. Возможно, это моя личная особенность.

sgrechnev
19.11.2017 18:23Постараюсь сделать свою критику максимально конструктивной.
Согласен с BosonBeard: если уж имеется отсылка к каким-то формулам, то стоит их хоть где-то прописать. Иначе читаешь
Возьмём её вторую часть…
и думаешь, а что же это за формула?
Если применить первую часть формулы...
И если для y есть хоть какая-то формула, то для x только конкретные вычисления.
Фактические неточности.
Если быть точным, то, пожалуй, A·sin(alpha) показывает, как делят гипотенузу sin^2(alpha) и cos^2(alpha), т.к.
A·sin(alpha) = C·sin^2(alpha)
(с учётом ОТТ).
- Обозначения и написание чисел.
Во-первых, традиционно в геометрии длины обозначаются строчными буквами, прописными — точки (но, конечно, это уж совсем не страшно).
Во-вторых, писать числа то с одной точностью, то с другой — как-то не очень хорошо. Тогда уж лучше остаться в общих обозначения a, b, c.
В целом, по прочтении Вашей статьи осталось больше вопросов, чем ответов. А хотелось бы иначе, раз уж Вы желаете рассказать об этом доступно, а не просто поднять тему.

dcc0 Автор
19.11.2017 18:55Окей. Все пункты принял к сведению.

sgrechnev
19.11.2017 20:18Благодарю!
Вот ещё момент, который сразу не заметил, но, думаю, стоит как-то поправить:
"… можно поэкспериментировать со следующим кодом, который вращает блок CSS div, который выступает в роли точки вращения."
С точки зрения русского языка, лучше написать иначе, что-то вроде "… кодом, вращающим CSS-div вокруг блока-точки вращения."

pilot911
19.11.2017 19:42допишите, пож-та, связь с матрицей и ее функциональность, то есть почему именно матрицей удобно оперировать

Psychosynthesis
20.11.2017 02:50Если б вы ещё рассказали где это всё веселье можно применить, статья стала бы минимум на порядок (в 10 раз!) полезнее.

FadeToBlack
20.11.2017 07:54Да, надо было начинать с определения проблемы, которую мы решаем, иначе статья «висит в воздухе». Для тех, кто знает ключевые слова, скорее всего, уже знает, как решать. Для тех, кто ключевых слов не знает — статью эту не найдет.


BosonBeard
Ожидал увидеть в статье, ну прям вот матрицу — матрицу, не увидел, но статья от этого менее полезной не стала =)
FadeToBlack
Потому что это можно объяснить проще и без матриц. На арифметике я уснул.
Sultansoy
А мне как раз таки решения с матрицами нравились намного больше и казались легче, но это скорее всего эффект математического анализа.
За статью спасибо, показали еще один прикольный способ, как объяснить студентам повороты.
dcc0 Автор
Вы преподаете математику?
Sultansoy
Иногда приходится преподавать математику. Чаще правда дискретную, но всяко бывает.
Так то я программист, но учился на прикмате, поэтому иногда просят помочь.
FadeToBlack
Если вы понимаете структуру матриц трансформации, что они состоят из базисных векторов, записанных в однородных координатах проективной геометрии, вам, конечно, одинаково понятны любые записи и любые объяснения. Но штурм девственного мозга программистов, которые не знают(забыли) матчасть — задача творческая. Тут нужен подход индивидуальный, так что для покрытия большинства умов требуется более, чем один подход к объяснению.