Данный материал публикуется с расчетом на начинающих программистов и неспециалистов...

Однажды вечером после чтения книжек о путешествиях, — кажется, это были знаменитое «Путешествие из Петербурга в Москву» Радищева и «Тарантасъ» Владимира Соллогуба — я сел смотреть лекцию об алгоритме Дейкстры. Смотрел, рисовал что-то на бумажке и нарисовал ориентированный граф. После некоторых размышлений мне стало интересно, как бы я реализовал алгоритм поиска всех путей из одной начальной точки (a) в какую-то другую единственную конечную точку (f) на ориентированном графе. Я уже было начал читать об алгоритмах поиска в глубину и ширину , но мне подумалось, что интереснее было бы попробовать «изобрести» алгоритм заново, часто ведь при таком подходе можно получить интересную модификацию уже известного алгоритма. Заодно я поставил себе несколько условий: 1 ) не использовать литературу; 2) использовать нерекурсивный подход; 3) хранить ребра в отдельных массивах, без вложенности. Далее постараюсь описать процесс поиска алгоритма и его реализации, как обычно на PHP.

Сам граф получился такой:


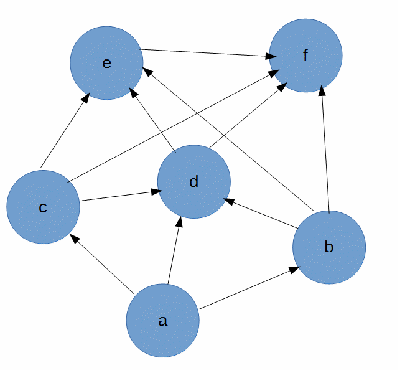
В общем: на входе ориентрованный граф с шестью вершинами, задача найти все пути из а в f без рекурсии и с минимальными затратами средств.

Ребра хранятся в нескольких массивах, имя массива — вершина:

$a=array('b','c','d');
$b=array('d','e','f');
$c=array('d','e','f');
$d=array('e','f');
$e=array('f');

Чтобы получить первый путь, я решил пройтись по нулевым индексам каждого массива и склеить их в одну строку х (в этой переменной на каждом этапе будет хранится найденный путь). Но как это сделать с минимальными затратами?! Мне показалось, что самым простым вариантом будет ввести еще один массив — инициализирующий.
В массиве int все элементы, которые есть в графе в обратном порядке.

$int=array('f','e','d','c','b','a'); 

Тогда получить первый путь очень просто, достаточно пройтись циклом по всем массивам,
добавлять в х новое значение с помощью конкатенации, и на каждом этапе использовать элемент из предыдущего массива в качестве указателя на следующий массив.

Этот стиль немного напоминает bash, но код выглядит довольно понятным:

	$x='a';
	$z=$a[0];
while (1) {
	$x.=$z; 
	$z=${$z}[0];
	if ($z == 'f') {$x.=$z;  break ;}
}

И так, мы получили первый путь x=abdef .

Можем вывести его на экран и заняться непосредственно самим алгоритмом, так как все, что было выше, — это только подготовительная часть. По идее от нее можно было бы избавиться, но я ее оставляю и публикую, чтобы был лучше понятен ход мысли.

Выводим на экран первый путь и запускаем первую функцию.

print $x;
print '<br>';
search_el ($x,$a,$b,$c,$d,$e);

Сам алгоритм фактически сводится к двум циклам, которые вынесены в отдельные функции.
Первая функция принимает полученный ранее первый путь x. Далее в цикле осуществляется обход x справа налево. Мы ищем два элемента, один из которых будет
работать в качестве указателя на массив, другой (правый, тут только стоит помнить, что массив перевернут) в качестве указателя на элемент массива. С помощью array_search найдем ключ элемента и проверим, есть ли что-нибудь в данном массиве после него. Если есть, то заменим элемент на найденный, но перед этим отрежем хвост (для этого нужен substr). Замену можно организовать и по другому:

function search_el($x, $a, $b, $c, $d, $e)
	{
	$j = strlen($x);
	while ($j != 0)
		{
		$j--;
		if (isset(${$x[$j - 1]})) 
         $key = array_search($x[$j], ${$x[$j - 1]});
		if (${$x[$j - 1]}[$key + 1] != '')
			{
			$x = substr($x, 0, $j);
			$x.= ${$x[$j - 1]}[$key + 1];
			new_way_search($x, $a, $b, $c, $d, $e);
			break;
			}
		}
	}

Условие с isset нужно, чтобы интерпретатор не выбрасывал предупреждение. К самому алгоритму оно отношения не имеет. Если никаких элементов в массивах найдено не было, то алгоритм завершится, но если все-таки чудо свершилось, то переходим в новую функцию, суть которой крайне проста — дописать хвост к x, вывести на экран и… «дорисовать восьмерку» или петлю — вернуться в функцию, из которой мы пришли, но уже с новым значением x:

function new_way_search($x, $a, $b, $c, $d, $e)
	{
	$z = $x[strlen($x) - 1];
	$z = ${$z}[0];

	while (1)
		{
		$x.= $z;
		if ($x[strlen($x) - 1] == 'f') break;

		if ($z == 'f')
			{
			$x.= $z;
			break;
			}

		$z = ${$z}[0];
}
	echo $x;
	echo '<br />';
	search_el($x, $a, $b, $c, $d, $e);
}

Результат работы алгоритма для графа, что на рисунке выше:

abdef
abdf
abef
abf
acdef
acdf
acef
acf
adef
adf

UPDATE:
В качестве дополнения приведу описание полученного алгоритма более кратко:
Ребра ориентированного графа выписаны в отдельные массивы в порядке возрастания.
Т.е. вершины графа и рёбра упорядочены. Это обязательное условие.
До начала алгоритма находим первый путь, который с учетом первого условия будет с минимальными именами вершин. Способ нахождения не особенно важен.

Описание для проверки на бумаге:
На входе первый найденный путь x=abdef:

1) Двигаемся справа налево по массиву х, выделяем два соседних элемента
(кроме последнего) abd[e]f, левый (d) используем в качестве указателя на массив
с вершиной, правый (e) в качестве указателя на элемент этого массива.
Ищем элемент в d после е, если он есть, убираем в x справа от e все элементы. Получаем в x=abde. Заменяем правый элемент (е) на найденный элемент.

2) Дописываем (вторым циклом) правую часть от элемента (или индекса правого элемента), который был заменен и до последнего элемента (f). В этом цикле требуется брать всегда массивы с 0 индексом, так как массивы упорядочены по условию. В данном случае мы сразу получили в правой части последний элемент x=abdf, поэтому второй цикл сработает вхолостую.

3) После формирования правой части возвращаемся к обходу массива справа налево.
Отсутствие элементов в первой вершине (массив а) — условие выхода из алгоритма.

Тот же код без функций и рекурсии, первый путь в x задан:

P.S.

Немного о методологии вместо заключения.

В итоге для разработки подобных алгоритмов получился довольно простой метод, который может быть полезен в работе с динамическими массивами.
Общая его суть — проведение подготовительных действий перед запуском основного алгоритма, для упрощения реализации. Это также должно делать алгоритм более прозрачным и понятным, что в свою очередь в дальнейшем должно способствовать его оптимизации и упрощению.

В данном случае методика разбивается на три подготовительных шага:
1) Определение наличия порядка в данных. Упорядочивание, если необходимо.
2) Введение инциализирующего (вектора) массива на упорядоченных данных.
3) Получение начального пути на основе предыдущего шага, смысл которого также состоит в упрощении основного алгоритма. В данном случае начальный путь также должен строиться с учетом порядка данных так, чтобы не получилось пропуска какого-либо пути.
Если на вершинах графа нет порядка, то может понадобиться дополнительный шаг, переопределение названий вершин, фактически построение изоморфного графа и создание массива соответствий (например, между реальными названиями городов и буквами алфавита). Для других случаев алгоритмизации вынесение исходного пути (вектора) за пределы циклов позаимствовано мной из моих прошлых статей о порождении комбинаторных объектов: перестановок , разбиений/композиций, сочетаний, размещений.

Если говорить о конкретных рабочих реализациях, то конечно, стоит внимательно изучить возможности того или иного языка по работе с динамическими данными. В данной ситуации использование «переменных переменных» для определения значения одной переменной в качестве названия для другой является лишь способом демонстрации корректности самого алгоритма. Какие существуют риски при использовании данного подхода в рабочих условиях, автору неизвестно.