В процессе реализации одной «считалки» возникла проблема с повышенной точностью вычислений. Расчетный алгоритм работал быстро на стандартных числах с плавающей запятой, но когда подключались библиотеки для точных вычислений, все начинало дико тормозить. В этой статье будут рассмотрены алгоритмы расширения чисел с плавающей запятой с помощью мультикомпонентного подхода, благодаря которому удалось достичь ускорения, так как float арифметика реализована на кристалле цп. Данный подход будет полезен для более точного вычисления численной производной, обращение матриц, обрезке полигонов или других геометрических задач. Так возможна эмуляции 64bit float на видеокартах, которые их не поддерживают.

Введение

Как завещал нам еще Никлуас Вирт хранить числа в 0 и 1, так мы их в них и храним. И ничего, что человеки живут в десятичной системе исчисления, и обычные казалось бы числа 0.1 и 0.3 не представимы в двоичной системе конечной дробью? Мы же испытываем культурный шок когда производим над ними вычисления. Кончено, предпринимаются попытки создания библиотек для процессоров на основе десятичной системы и IEEE даже стандартизировал форматы.

Но пока мы везде учитываем бинарность хранения и проводим все денежные вычисление с библиотеками для точного вычисления, такими как bignumber, что приводит к потере производительности. Асики считают крипту, а в процессорах и так мало места для этой вашей десятичной арифметики, считают маркетологи. Поэтому мультикомпонентный подход, когда число хранится в виде непреобразованной суммы чисел, это удобный трюк и активно развивающаяся сфера в области теоретической информатики. Хотя умножать правильно, без потери точности еще научился Деккер в 1971, готовые к применению библиотеки появились значительно позже (MPFR, QD) и не во всех языках, видимо так как не все поддерживали стандарты IEEE, а строгие доказательства погрешности вычислений и того позже, например в 2017 для double-word арифметики.

Double-word арифметика

В чем суть? В бородатые времена, когда еще не было стандартов для плавающих чисел, что бы избежать проблем с реализацией их округления, Moller придумал, а Knuth в последствии доказал, что существует свободное от ошибок суммирование. Выполняющееся таким образом

function quickTwoSum(a, b) {
  let s = a + b;
  let z = s - a;
  let e = b - z;
  return [s, e];
}

В данном алгоритме предполагалось, что если $$, то точная их сумма представима в виде суммы двух чисел $$ и можно хранить их парой для последующих вычислений, а вычитание сводится к сложению с отрицательным числом.



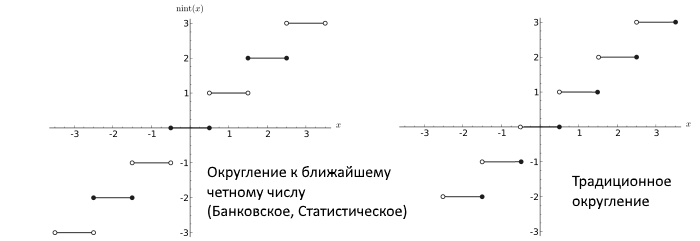
В последствии Dekker показал, что если используются числа с плавающей запятой, использующие округление к ближайшему четному числу (round-to-nearest ties to even, что вообще является правильной процедурой, не приводящей к большим погрешностям в процессе долгих вычислений и стандартом по IEEE), то существует алгоритм умножения, свободный от ошибок.

function twoMult(a, b) {
  let A = split(a);
  let B = split(b);
  let r1 = a * b;
  let t1 = -r1 + A[0] * B[0];
  let t2 = t1 + A[0] * B[1];
  let t3 = t2 + A[1] * B[0];
  return [r1, t3 + A[1] * B[1]];
}

где split() это алгоритм господина Veltkamp'а для разделения числа

let splitter = Math.pow(2, 27) + 1;

function split(a) {
  let t = splitter * a;
  let d = a - t;
  let xh = t + d;
  let xl = a - xh;
  return [xh, xl];
}

использующий константу $$, которую приравнивают чуть больше половины длины мантиссы, что не приводит к переполнению чисел в процессе умножения и разделяет мантиссу на две половины. Например при длине слова в 64-bit, длина мантиссы равна 53 и тогда s=27.



Таким образом Dekker привел почти полный набор, необходимый для вычисления в double-word арифметике. Так как там еще было указано как умножать, делить и возводить в квадрат два double-word числа.

У него был везде «заинлайнен» алгоритм quickTwoSum для суммирования двух double-word, и использовалась проверка $$. На современных процессорах, как описано в [4], дешевле использовать дополнительные операции с числами, чем ветвление алгоритма. Поэтому следующий алгоритм, сейчас более уместен для сложения двух single-word чисел

function twoSum(a, b) {
  let s = a + b;
  let a1 = s - b;
  let b1 = s - a1;
  let da = a - a1;
  let db = b - b1;
  return [s, da + db];
}

А вот так производится суммирование и умножение double-word чисел.

function add22(X, Y) {
  let S = twoSum(X[0], Y[0]);
  let E = twoSum(X[1], Y[1]);
  let c = S[1] + E[0];
  let V = quickTwoSum(S[0], c);
  let w = V[1] + E[1];
  return quickTwoSum(V[0], w);
}

function mul22(X, Y) {
  let S = twoMult(X[0], Y[0]);
  S[1] += X[0] * Y[1] + X[1] * Y[0];
  return quickTwoSum(S[0], S[1]);
}

Вообще говоря, самый полный и точный список алгоритмов для double-word арифметики, теоретические границы ошибок и практическая реализация описана в ссылке [3] от 2017 года. Поэтому если заинтересовало, настоятельно рекомендую идти сразу туда. И вообще, в [6] приведен алгоритм для quadruple-word, а в [5] для мультикомпонентного расширения произвольной длины. Только вот там, после каждой операции используется процесс ренормализации, что не всегда оптимально для малых размеров, а точность вычислений в QD не определена строго. Вообще стоит задумываться о границах применимости данных подходов, конечно.

Страшилки javascript-a. Сравнение decimal.js vs bignumber.js vs big.js.

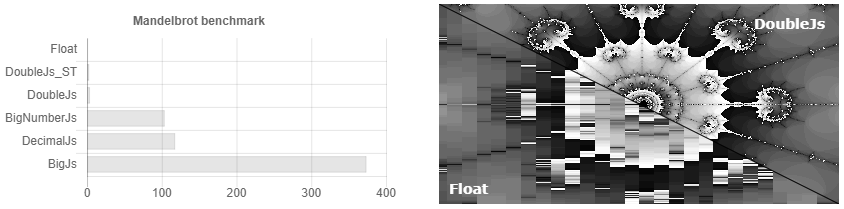
Так получилось что почти все библиотеки для точных вычислений в js написаны одним человеком. Создается иллюзия выбора, хотя они почти все одинаковые. В добавок в документации явно не указано, что если вы не будете округлять числа после каждой операции умножения/деления, то размер вашего числа будет все время удваиваться, и сложность алгоритма может вырасти в легкую в x3500. Например вот так может выглядеть сравнение их времени вычисления, если вы не округляли числа.



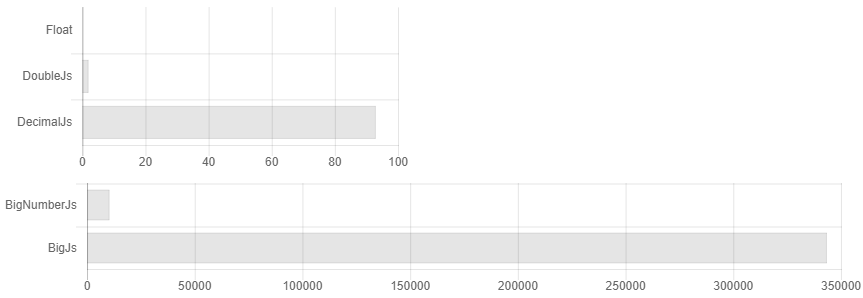
То есть вы выставляете точность в 32 знак после запятой и… Упс у вас уже 64 знака, 128. Мы считаем очень точно! 256, 512… Но я выставлял 32!.. 1024, 2048… Как то так появляется overhead в 3500 раз. В документации указано, что если у вас научные вычисления, то вероятно вам лучше подойдет decimal.js. Хотя по факту, если просто периодически округлять, для научных вычислений Bignumber.js работает чуть шустрее (см. рис. 1). Кому то нужно считать сотые доли копеек, если их нельзя выдать сдачей? Есть ли какой то кейс, когда надо хранить больше указных чисел и не выкрутится еще несколькими дополнительными знаками? Как оно возьмет синус от такого числа-монстра, когда строгую точность сходимости ряда тейлора для произвольных чисел никто не знает. Вообщем есть не безосновательные подозрения, что там можно увеличить скорость расчета, используя алгоритмы умножения Шёнхаге — Штрассена и нахождения синуса с Cordic вычислениями, например.

Double.js

Мне бы хотелось сказать, конечно, что Double.js считает быстро и точно. Но это не совсем так, то есть быстрее в 10 раз то оно считает, да вот не всегда точно. Например 0.3-0.1 оно умеет обрабатывать, переходя в удвоенное хранение и обратно. Но вот число Pi распарсить с удвоенной точностью в почти 32 знака и обратно у него не выходит. Образуется ошибка на 16-м, как будто происходит переполнение. Вообщем, я призываю js сообщество общими усилиями попробовать решить проблему парсинга, так как я застрял. Пробовал парсить поцифренно и делить в двойной точности, как в QD, делить пачками по 16 цифр и делить в двойной точности, сплитить мантиссу используя Big.js как в одной из либ Julia. Сейчас я грешу на баг в .parseFloat(), так как IEEE стандарты с округлением к ближайшему целому поддерживаются еще с ECMAScript 1. Хотя конечно можно попробовать забиндить двоичный buffer и наблюдать за каждым 0 и 1. Вообщем, если получится разрешить данную проблему, тогда можно будет тогда сделать вычисления с произвольной точностью с ускорением в x10-x20 от bignumber.js. Впрочем множество Мандельброта оно уже сейчас рендерит качественно, и можно использовать ее для геометрических задач.



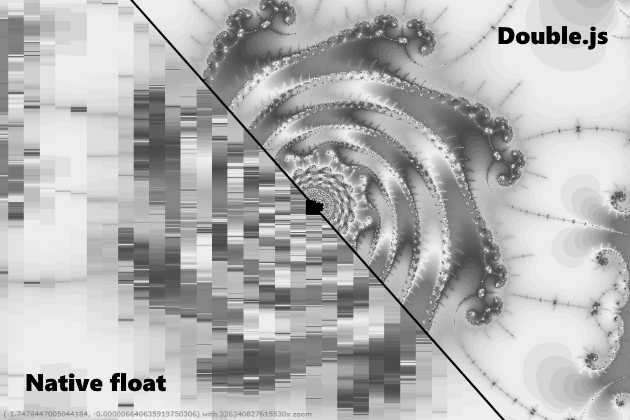
Вот ссылка на либу, там есть интерактивный benchmark и песочица, где можно с ней поиграть.

Используемые источники

1. O. Moller. Quasi double precision in floating-point arithmetic., 1965.
2. Theodorus Dekker. A floating-point technique for extending the available precision, 1971. [Viewer]
3. Mioara Joldes, Jean-Michel Muller, Valentina Popescu. Tight and rigourous error bounds for basic building blocks of double-word arithmetic, 2017. [PDF]
4. Muller, J.-M. Brisebarre, N. de Dinechin, etc. Handbook of Floating-Point Arithmetic, Chapter 14, 2010.
5. Jonathan Shewchuk. Robust Adaptive Floating-Point Geometric Predicates, 1964. [PDF]
6. Yozo Hida, Xiaoye Li, David Bailey. Library for Double-Double and Quad-Double Arithmetic, 2000. [PDF]