28.10.2018 01:50
Nookie-Grey 19 3500 Источник
Все мы знаем из школьного курса что такое системы счисления(СС). Но не все задумываются о том, на сколько затратны СС. Т.е. какой набор цифр нам необходим для представления числа в данной СС. Когда у нас есть ограниченный набор уникальных элементов (разноцветные камушки разных размеров), с помощью которого мы можем представить число, какое максимальное число мы можем представить используя эти элементы? (все красные камушки — это ноль, зелёные — один, синие — два и т.д., маленькие — нулевой разряд, средние — первый, большие — второй и т.д.). Где та грань, при которой основание СС играет большую роль чем разрядность числа?

Возьмём для примера n — количество элементов, равным 60. Разбив элементы на 2 группы (двоичная система счисления) мы получим 30 разрядов. 30 единиц — самое больше 30-ти разрядное число с основанием 2. Если к нему прибавить 1, то получим единицу с 30 нулями, т.е. 2 в 30-ой, так как каждый ноль — это степень двойки, а разряды начинаются с 0, и не забудем вычесть единицу, которую прибавили.

Для других СС аналогично $y=x^{60/x}-1$, где y — максимальное число, x — основание степени.

Точки построения:

$2^{30}-1=1\,073\,741\,823$.
$3^{20}-1=3\,486\,784\,400$.
$4^{15}-1=1\,073\,741\,823$
$5^{12}-1=244\,140\,624$
$6^{10}-1=60\,466\,175$
$10^{6}-1=999\,999$
$12^{5}-1=248\,831$

График функции:

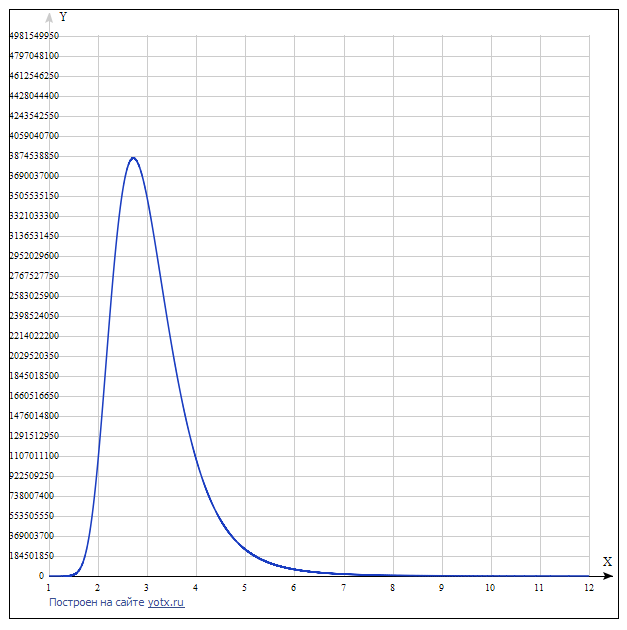
image

Из графика видно, что с увеличением основания СС, начиная с трёх, затратность её увеличивается и функция имеет верхний экстремум. Приведя её к общему виду можно получить $y=(\sqrt[x]x)^{n}-1$, а максимум функции $\sqrt[x]x$ достигается при $x=e$.

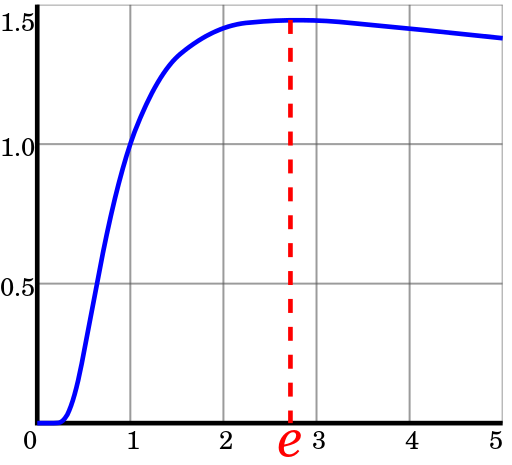
image

График функции $y=\sqrt[x]x$

Т.е. самая экономичная СС — это система, максимально близкая к $e$ или 3.

P.S.: По мимо того СС с основанием 3 — нечётная, а значит не имеет проблемы округления (привести 0.5 к 0 или к 1), а если цифры записывать симметрично (-1,0,1 вместо 0,1,2) то появляется простота представления отрицательных чисел (10-1 это 8, -101 это -8, где минус — это не знак, а часть цифры, которую можно заменить на Z), но это уже совсем другая арифметика)))

Комментарии (19)


  1. LexS007
    28.10.2018 05:42
    #19292741
    +2

    Некая работа конечно проделана, но эти же результаты уже многократно упоминались в статьях о троичной сс и троичном компьютере. Даже на wikipedia есть эта инфа:

    Удельное натуральнологарифмическое число кодов (чисел) (плотность записи информации) описывается уравнением y=ln(x)/x, где x — основание системы счисления. Из уравнения следует, что наибольшей плотностью записи информации обладает система счисления с основанием равным основанию натуральных логарифмов, то есть равным числу Эйлера (е=2,71…). Эту задачу решали ещё во времена Непера при выборе основания для логарифмических таблиц. Из целочисленных систем счисления наибольшей плотностью записи информации обладает троичная система счисления.


  1. FadeToBlack
    28.10.2018 06:55
    #19292781

    А почему бы вам не написать, какие преимущества можно получить за счет более экономичной системы счисления? Причем не те преимущества, которые написаны в википедии (данные давно минувших дней), а где это реально можно применить в современности?


  1. maxzhurkin
    28.10.2018 08:03
    #19292829
    -1

    Есть только одна проблема с этим «исследованием»: оно основано на умозрительной системе на основе камней, а если, например, взять любую систему счисления с основанием 2 в степени n, то с использованием двоичной системы «под капотом», она становится столь же эффективной, как и двоичная


  1. longtolik
    28.10.2018 08:52
    #19292877

    Природа для кодирования ДНК использует основание 4, но это, видимо, из-за того, что буквы должны быть парными (комплементарными).


    1. OKyJIucT
      28.10.2018 10:14
      #19293027
      +2

      Не все в природе делается оптимальным образом. Просто в один прекрасный момент существа с ДНК на основе 4 оснований выжили, в то время как другие (если они в принципе существовали) — нет.
      Думаю, вполне реально было сделать ДНК и из трёх азотистых оснований, где каждый с каждым тоже мог бы кодировать информацию определенным образом.


      1. Peacemaker
        28.10.2018 21:40
        #19294897

        Думаю, вполне реально было сделать ДНК и из трёх азотистых оснований, где каждый с каждым тоже мог бы кодировать информацию определенным образом.

        Тогда восстановить вторую линию спирали ДНК по первой было бы невозможно.


        1. OKyJIucT
          28.10.2018 21:44
          #19294909

          Тогда обе спирали по факту и не нужны, достаточно одной, если, зная ее, можно получить вторую. Значит, не оптимальное решение выбрала природа :)


          1. Denai
            28.10.2018 22:12
            #19294991

            Вы упускаете то для чего эта возможность вообще нужна и отталкиваетесь от того что в ней нет смысла.


            1. OKyJIucT
              28.10.2018 22:16
              #19295013

              Не упускаю, но могло бы и с двумя основаниями все существовать, конечно, многие механизмы работы были бы другие. Но по факту, если спираль разъединить, то наследственная информация не станет менее целостной. Из нее все так же можно будет сделать полную рабочую копию.


              1. Caseor
                29.10.2018 02:41
                #19295471

                РНК ЕМНИП копирует кусок ДНК, являясь одной половинкой развёрнутой ДНК.

                з.ы. ниже уже написали.


          1. agathis
            29.10.2018 00:42
            #19295329

            Ты бывают рнк-вирусы, например.
            А две комплементарных цепочки — это raid1 по сути :)


            1. OKyJIucT
              29.10.2018 00:43
              #19295335

              В точку! Шикарная аналогия :)


    1. dimitri26
      29.10.2018 07:32
      #19295645

      У ДНК две нити, а молекула коллагена представляет собой спираль из трёх нитей. Но это совсем другая история…


  1. da-nie
    28.10.2018 13:46
    #19293631

    но это уже совсем другая арифметика


    А в машине «Сетунь» вроде как эта арифметика и была.


    1. Nookie-Grey Автор
      28.10.2018 14:00
      #19293689

      К сожалению в ней имитировались триты, т.е. использовалось 2 бита на один трит, а четвёртое значение отбрасывалось.


      1. da-nie
        28.10.2018 15:34
        #19293983

        Разве там не использовались ферритовые сердечники с тремя состояниями (два варианта намагниченности и отсутствие намагниченности)?


        1. Nookie-Grey Автор
          28.10.2018 18:11
          #19294421
          +1

          На хабре аж 17 статей про Сетунь. В одной из них чётко говориться что использовалось два сердечника, которые могли представить 2 бита.

          Троичная логика была реализована через объединение двух таких ферритовых элементов и подключения их таким образом, что они моделировали три устойчивых состояния. Этот подход был успешным, но количество необходимых элементов не сокращалось, поскольку в действительности два ферритовых сердечника могут потенциально представлять собой два двоичных бита, что в итоге даёт больший объём информации (2 ^ 2), чем один троичный «трит» (3 ^ 1), Печально, но хотя бы потребляемая мощность была снижена!
          Компьютеры Советской России с троичной сбалансированной системой счисления

          Здесь так же говорится, что
          При работе машина использовала двухбитный троичный код.


  1. kokorins
    29.10.2018 00:02
    #19295217

    то есть это только с фиксированным основанием? а как насчёт разложения по числам Фибоначчи или что-то подобное?


    1. a5b
      29.10.2018 02:52
      #19295481

      https://ru.wikipedia.org/wiki/Система_счисления#Смешанные_системы_счисления
      https://ru.wikipedia.org/wiki/Фибоначчиева_система_счисления