В этой статье Вы узнаете всё о Вавилонской библиотеке, а самое главное — как воссоздать её, да и вообще любую библиотеку.

Начнём с цитат произведения «Вавилонская библиотека» Луиса Борхеса.


Если Вы войдёте в случайный шестиугольник, подойдёте к любой стене, взглянете на любую полку и возьмёте больше всего понравившуюся вам книгу, то, скорее всего, огорчитесь. Ведь Вы ожидали узнать там о смысле жизни, но увидели какой-то непонятный набор символов. Но не стоит так быстро огорчаться! Большая часть книг бессмысленна, ибо они представляют собой комбинаторный перебор всех возможных вариантов двадцати пяти знаков (именно такой алфавит использовал Борхес в своей библиотеке, но далее читатель узнает, что в библиотеке может быть сколько угодно символов). Главный закон библиотеки — в ней не существует двух абсолютно одинаковых книг, соответственно их число конечно, и библиотека тоже когда-нибудь закончится. Борхес же считал, что библиотека периодична:


В сравнении с бессмыслицей, книг, содержание которых человек может хоть как-то понять, очень мало, но это не меняет того факта, что библиотека содержит все тексты, которые были и будут когда-либо придуманы человеком. Да и к тому же Вы с детства привыкли считать одни последовательности символов оссмысленными, а другие — нет. На самом деле, в контексте библиотеки разницы между ними нет. Но то, что имеет смысл, имеет куда меньший процент, и мы называем это языком. Это средство общения между людьми. Любой язык содержит в себе всего несколько десятков тысяч слов, из которых мы знаем 70% от силы, отсюда и получается, что большую часть комбинаторного перебора книг интерпретировать мы не можем. А кто-то страдает апофенией и даже в случайных наборах символов видит скрытый смысл. А ведь это неплохая идея для стеганографии! Что ж, продолжить обсуждение этой темы предлагаю в комментариях.

Перед тем, как перейти к реализации этой библиотеки, удивлю вас интересным фактом: если Вы захотите воссоздать Вавилонскую библиотеку Луиса Борхеса, у вас ничего не получится, ибо её объёмы превосходят объём видимой Вселенной в 10^611338 (!) раз. А о том, что будет происходить в ещё более крупных библиотеках, мне даже страшно подумать.

Реализация библиотеки

Описание модуля

Наше небольшое вступление закончилось. Но оно не лишено смысла: теперь Вы понимаете, что из себя представляет Вавилонская библиотека, и читать дальше будет только интереснее. Но я уйду от изначальной идеи, мне хотелось создать «универсальную» библиотеку, о которой речь пойдёт далее. Писать буду на JavaScript под Node.js.Что должна уметь библиотека?

• Быстро находить нужный текст и выдавать его дислокацию в библиотеке
• Определять название книги
• Быстро находить книгу с нужным названием

Помимо этого, она должна быть универсальной, т.е. любой из параметров библиотеки может быть изменён, если я этого захочу. Что ж, я думаю, что сначала покажу весь код модуля, мы его детально разберём, посмотрим, как он работает, и я выскажу несколько слов. Github-репозиторий

Главный файл — index.js, там описана вся логика библиотеки, содержимое этого файла я и буду объяснять.

let sha512 = require(`js-sha512`);

Подключаем модуль, реализующий алгоритм хеширования sha512. Вам это может показаться странным, но он нам ещё пригодится.
Что на выходе у нашего модуля? Он возвращает функцию, вызов которой вернёт объект библиотеки со всеми нужными методами. Мы могли бы вернуть его сразу, но тогда управление библиотекой не было бы таким удобным, когда мы передаём параметры в функцию и получаем «нужную» библиотеку. Это и позволит нам создать «универсальную» библиотеку. Поскольку я стараюсь писать в стиле ES6, то моя стрелочная функция принимает в качестве параметров объект, который впоследствии будет деструктурирован на нужные переменные:

module.exports = ({
	lengthOfPage = 4819, 
	lengthOfTitle = 31, 
	digs = '0123456789abcdefghijklmnopqrstuvwxyz', 
	alphabet = 'абвгдеёжзийклмнопрстуфхцчшщъыьэюя, .',
	wall = 5,
	shelf = 7,
	volume = 31,
	page = 421,
} = {}) => {
        //немного магии... 
};

Теперь пробежимся по параметрам. В качестве стандартных числовых параметров я решил выбрать простые числа, ибо мне показалось, что так будет интереснее.

• lengthOfPage — число, количество символов на одной странице. По умолчанию 4819. Если факторизовать это число, получим 61 и 79. 61 строка по 79 символов, или наоборот, но мне предпочтительнее первый вариант.
• lengthOfTitle — число, количество символов в названии заголовка книги.
• digs — строка, возможные цифры числа с основанием, равным длине этой строки. Для чего это число нужно? В нём будет содержаться номер (идентификатор) шестигранника, в который мы хотим перейти. По умолчанию это латиница в нижнем регистре и цифры 0-9. Большая часть текста закодирована именно здесь, поэтому это будет большое число — несколько тысяч разрядов (зависит от количества символов на странице), но работа с ним будет производиться посимвольно.
• alphabet — строка, символы, которые мы хотим видеть в библиотеке. Она будет наполнена именно ими. Чтобы всё работало правильно, количество символов алфавита должно равняться количеству символов в строки с возможными цифрами числа, идентефицирующего шестигранник.
• wall — число, максимальный номер стены, по умолчанию 5
• shelf — число, максимальный номер полки, по умолчанию 7
• volume — число, максимальный номер книги, по умолчанию 31
• page — число, максимальный номер страницы, по умолчанию 421

Как вы можете заметить, это мало походит на настоящую Вавилонскую библиотеку Луиса Борхеса. Но я уже не раз говорил, что мы будем создавать «универсальные» библиотеки, которые могут быть такими, какими мы захотим их увидеть (поэтому номер шестигранника можно начать интерпретировать как-то иначе, нап. просто идентификатор какого-то места, где хранится нужная информация). Вавилонская библиотека — лишь одна из них. Но у всех них много общего — за их работоспособность отвечает один алгоритм, о котором сейчас пойдёт речь.

Алгоритмы поиска и выдачи страниц

Когда мы переходим по какому-то адресу, мы видим содержимое страницы. Если мы ещё раз перейдём по тому же адресу, содержимое должно быть абсолютно таким же. Данное свойство библиотек обеспечивает алгоритм генерации псевдослучайных чисел — Линейный конгруэнтный метод. Когда нам нужно выбрать символ для генерации адреса или, наоборот, содержимого страницы, он будет нам помогать, а в качестве зерна будут использоваться номера страниц, полок и т.д. Конфиг моего ГПСЧ: m = 2^32 (4294967296), a = 22695477, c = 1. Хочется ещё добавить, что в нашей реализации от линейного конгруэнтного метода остался лишь принцип генерации чисел, остальное изменено. Двигаемся по листингу программы дальше:


Как вы можете заметить, зерно ГПСЧ меняется после каждого получения числа, и результаты напрямую зависят от так называемой точки отсчёта — зерна, после которого числа будут нас интересовать. (мы генерируем адрес или получаем содержимое страницы)

Функция getHash поможет нам сгенерировать точку отсчёта. Мы просто получим хеш от каких-то данных, возьмём 7 символов, переведём в десятичную систему счисления и готово!

Функция mod ведёт себя так же, как и оператор %. Но в случае, если делимое a < 0 (такие ситуации возможны), функция mod вернёт положительное число за счёт особой структуры, нам это нужно, чтобы правильно выбирать символы из строки alphabet при получении содержимого страницы по адресу.

И последний кусок кода на десерт — возвращаемый объект библиотеки:


В начале мы записываем в него свойства библиотеки, которые я описывал ранее. Вы можете изменить их даже после завершения вызова главной функции (которую, в принципе, можно называть конструктором, но мой код слабо похож на классовую реализацию библиотеки, поэтому ограничусь словом «главной»). Возможно, такое поведение не совсем адекватно, но зато гибко. Теперь пробежимся по каждому методу.

Метод search

search(searchStr) {
    let wall = `${(Math.random() * this.wall + 1 ^ 0)}`,
        shelf = `${(Math.random() * this.shelf + 1 ^ 0)}`,
        volume = pad(`${(Math.random() * this.volume + 1 ^ 0)}`, 2),
        page = pad(`${(Math.random() * this.page + 1 ^ 0)}`, 3),
        locHash = getHash(`${wall}${shelf}${volume}${page}`), 
        hex = ``,
        depth = Math.random() * (this.lengthOfPage - searchStr.length) ^ 0;
    for (let i = 0; i < depth; i++){
        searchStr = alphabet[Math.random() * alphabet.length ^ 0] + searchStr;
    }
    seed = locHash;
    for (let i = 0; i < searchStr.length; i++){
        let index = alphabetIndexes[searchStr[i]] || -1,
            rand = rnd(0, alphabet.length),
            newIndex = mod(index + parseInt(rand), digs.length), 
            newChar = digs[newIndex];
        hex += newChar;
    }
    return `${hex}-${wall}-${shelf}-${+volume}-${+page}`; 
}

Возвращает адрес строки searchStr в библиотеке. Для этого случайным образом выбираем wall, shelf, volume, page. volume и page также дополняем нулями до нужной длины. Далее конкатенируем их в строку для передачи в функцию getHash. Полученный locHash — и есть начальная точка отсчёта, т.е. зерно.

Для большей непредсказуемости дополняем searchStr depth псевдослучайными символами алфавита, присваиваем зерну seed значение locHash. На данном этапе неважно, как мы будем дополнять строку, поэтому можно использовать встроенный в JavaScript ГПСЧ, это некритично. Можно и вовсе от него отказаться, чтобы интересующие нас результаты были всегда в начале страницы.

Осталось дело за малым — сгенерировать идентификатор шестигранника. Для каждого символа строки searchStr выполняем алгоритм:

1. Получить номер символа index в алфавите из объекта alphabetIndexes. Если его нет, вернуть -1, но если такое произошло, вы определённо что-то делаете не так.
2. Сгенерировать псевдослучайное число rand, используя наш ГПСЧ, в диапазоне от 0 до длины алфавита.
3. Вычислить новый индекс, который рассчитывается как сумма номера символа index и псевдослучайного числа rand, поделённая по модулю на длину digs.
4. Таким образом мы получили цифру идентификатора шестигранника — newChar (взяв её из digs).
5. Добавляем newChar к идентификатору шестигранника hex

По завершению генерации hex возвращаем полный адрес места, в котором содержится искомая строка. Компоненты адреса разделены дефисом.

Метод searchExactly

searchExactly(text) {
    const pos = Math.random() * (this.lengthOfPage - text.length) ^ 0;
    return this.search(`${` `.repeat(pos)}${text}${` `.repeat(this.lengthOfPage - (pos + text.length))}`);
}

Этот метод делает всё то же самое, что и метод search, но заполняет всё свободное пространство (делает искомую строку searchStr длиной в lengthOfPage символов) пробелами. При просмотре такой страницы будет казаться, что на ней нет ничего, кроме вашего текста.

Метод searchTitle

searchTitle(searchStr) {
    let wall = `${(Math.random() * this.wall + 1 ^ 0)}`,
        shelf = `${(Math.random() * this.shelf + 1 ^ 0)}`,
        volume = pad(`${(Math.random()* this.volume + 1 ^ 0)}`, 2),
        locHash = getHash(`${wall}${shelf}${volume}`), 
        hex = ``;
    searchStr = searchStr.substr(0, this.lengthOfTitle);
    searchStr = searchStr.length == this.lengthOfTitle ? searchStr : `${searchStr}${` `.repeat(this.lengthOfTitle - searchStr.length)}`;
    seed = locHash;
    for (let i = 0; i < searchStr.length; i++){
        let index = alphabetIndexes[searchStr[i]],
            rand = rnd(0, alphabet.length),
            newIndex = mod(index + parseInt(rand), digs.length),
            newChar = digs[newIndex];
        hex += newChar;
    }
    return `${hex}-${wall}-${shelf}-${+volume}`; 
}

Метод searchTitle возвращает адрес книги с названием searchStr. Внутри он очень похож на search. Отличие заключается в том, что при вычислении locHash мы не используем страницу, чтобы привязать к книге её название. Оно не должно зависеть от страницы. searchStr обрезается до длины lengthOfTitle и при необходимости дополняется пробелами. Аналогично генерируется идентификатор шестигранника и возвращается полученный адрес. Обратите внимание, в нём нет страницы, как это было при поиске точного адреса произвольного текста. Так что если хотите узнать, что находится в книге с придуманным Вами названием, определитесь со страницей, на которую хотите перейти.

Метод getPage

getPage(address) {
    let addressArray = address.split(`-`),
        hex = addressArray[0], 
        locHash = getHash(`${addressArray[1]}${addressArray[2]}${pad(addressArray[3], 2)}${pad(addressArray[4], 3)}`),
        result = ``;
    seed = locHash;
    for (let i = 0; i < hex.length; i++) {
        let index = digsIndexes[hex[i]],
            rand = rnd(0, digs.length),
            newIndex = mod(index - parseInt(rand), alphabet.length), 
            newChar = alphabet[newIndex];
        result += newChar;
    }
    seed = getHash(result);
    while (result.length < this.lengthOfPage) {
        result += alphabet[parseInt(rnd(0, alphabet.length))];
    }
    return result.substr(result.length - this.lengthOfPage);
}

Противоположен методу search. Его задача — по заданному адресу выдать содержимое страницы. Для этого преобразуем адрес в массив по разделителю "-". Теперь у нас есть массив компонентов адреса: идентификатор шестигранника, стена, полка, книга, страница. Вычисляем locHash так же, как это делали в методе search. Мы получим такое же число, которое было при генерации адреса. Это означает, что ГПСЧ будет выдавать такие же числа, именно это поведение и обеспечивает обратимость наших преобразований над исходным текстом. Для его вычисления над каждым символом (де-факто, это цифра) идентификатора шестигранника выполняем алгоритм:

1. Вычисляем index в строке digs. Возьмём его из digsIndexes.
2. Используя ГПСЧ, генерируем псевдослучайное число rand в диапазоне 0 до основания системы счисления большого числа, равной длине строки, содержащей цифры этого прекрасного числа. Всё очевидно.
3. Вычисляем позицию символа исходного текста newIndex как разность index и rand, поделённая по модулю на длину алфавита. Возможна ситуация, когда разность отрицательна, тогда обычное деление по модулю даст отрицательный индекс, что нас не устраивает, поэтому мы используем модифицированный вариант деления по модулю. (можно попробовать вариант со взятием абсолютного значения от приведённой выше формулы, это тоже решает проблему отрицательных чисел, но на практике это ещё не проверялось)
4. Символ текста страницы — newChar, получаем по индексу из алфавита.
5. Добавляем символ текста к результату.

Полученный на данном этапе результат не всегда заполнит всю страницу, поэтому вычислим новое зерно от текущего результата и заполним свободное место символами из алфавита. В выборе символа нам помогает ГПСЧ.

На этом вычисление содержимого страницы заканчивается, мы возвращаем его, не забыв обрезать до максимальной длины. Быть может, во входном адресе идентификатор шестигранника был неприлично большим.

Метод getTitle

getTitle(address) {
    let addressArray = address.split(`-`),
        hex = addressArray[0], 
        locHash = getHash(`${addressArray[1]}${addressArray[2]}${pad(addressArray[3], 2)}`),
        result = ``;
    seed = locHash;
    for (let i = 0; i < hex.length; i++) {
        let index = digsIndexes[hex[i]],
            rand = rnd(0, digs.length),
            newIndex = mod(index - parseInt(rand), alphabet.length),
            newChar = alphabet[newIndex];
        result += newChar;
    }
    seed = getHash(result);
    while (result.length < this.lengthOfTitle) {
        result += alphabet[parseInt(rnd(0, alphabet.length))];
    }
    return result.substr(result.length - this.lengthOfTitle);
}

Ну, тут такая же история. Представьте, что читаете описание предыдущего метода, только при вычислении зёрен ГПСЧ не учитываете номер страницы, а дополнение и обрезание результата производите до максимальной длины названия книги — lengthOfTitle.

Испытание модуля для создания библиотек

После того, как мы разобрали принцип работы любой вавилонско-подобной библиотеки — пора бы испытать это всё на практике. Буду использовать конфиг, максимально близкий к созданному Луисом Борхесом. Искать будем простую фразу «habr.com»:

const libraryofbabel = require(`libraryofbabel`)({
    lengthOfPage: 3200, 
    alphabet: `abcdefghijklmnopqrstuvwxyz, .`,
    //латиница, запятая, пробел, точка
    digs: `0123456789abcdefghijklmnopqrs`,
    //идентификатор - 29-ричное число
    wall: 4,
    shelf: 5,
    volume: 32,
    page: 410
    //конфиг Вавилонской библиотеки
});

//ищем истину
console.log(libraryofbabel.search(`habr.com`));

Запускаем, результат:



На данный момент это нам ничего не даёт. Но давайте же узнаем, что скрывается за этим адресом! Код будет таким:

const libraryofbabel = require(`libraryofbabel`)({
    lengthOfPage: 3200, 
    alphabet: `abcdefghijklmnopqrstuvwxyz, .`,
    //латиница, запятая, пробел, точка
    digs: `0123456789abcdefghijklmnopqrs`,
    //идентификатор - 29-ричное число
    wall: 4,
    shelf: 5,
    volume: 32,
    page: 410
    //конфиг Вавилонской библиотеки
});

const text = `habr.com`;
//наш текст

const adress = libraryofbabel.search(text);
//сохраняем адрес в переменную

const clc = require(`cli-color`);
//модуль для форматирования вывода из консоли

console.log(libraryofbabel.getPage(adress).replace(text, clc.green(text)));

Результат:



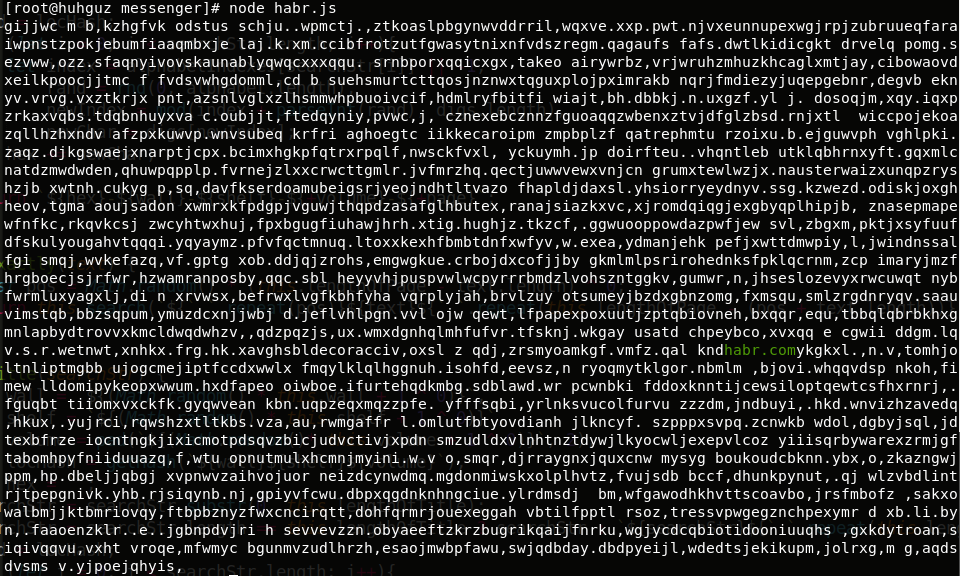
Мы нашли то, что искали, в бесконечном множестве бессмысленных (я б поспорил) страниц!

Но это далеко не единственное место, где находится эта фраза. При следующем запуске программы будет сгенерирован другой адрес. Если хотите — можете сохранять один и работать с ним. Главное, что содержимое страниц никогда не меняется. Давайте посмотрим на заголовок книги, в которой находится наша фраза. Код будет следующим:

const libraryofbabel = require(`libraryofbabel`)({
    lengthOfPage: 3200, 
    alphabet: `abcdefghijklmnopqrstuvwxyz, .`,
    //латиница, запятая, пробел, точка
    digs: `0123456789abcdefghijklmnopqrs`,
    //идентификатор - 29-ричное число
    wall: 4,
    shelf: 5,
    volume: 32,
    page: 410
    //конфиг Вавилонской библиотеки
});

const text = `habr.com`;
//наш текст

const adress = libraryofbabel.search(text);
//сохраняем адрес в переменную

const clc = require(`cli-color`);
//модуль для форматирования вывода из консоли

console.log(libraryofbabel.getPage(adress).replace(text, clc.green(text)));

console.log(`\nНазвание книги: ${clc.green(libraryofbabel.getTitle(adress))}`);

Название книги получилось примерно таким:



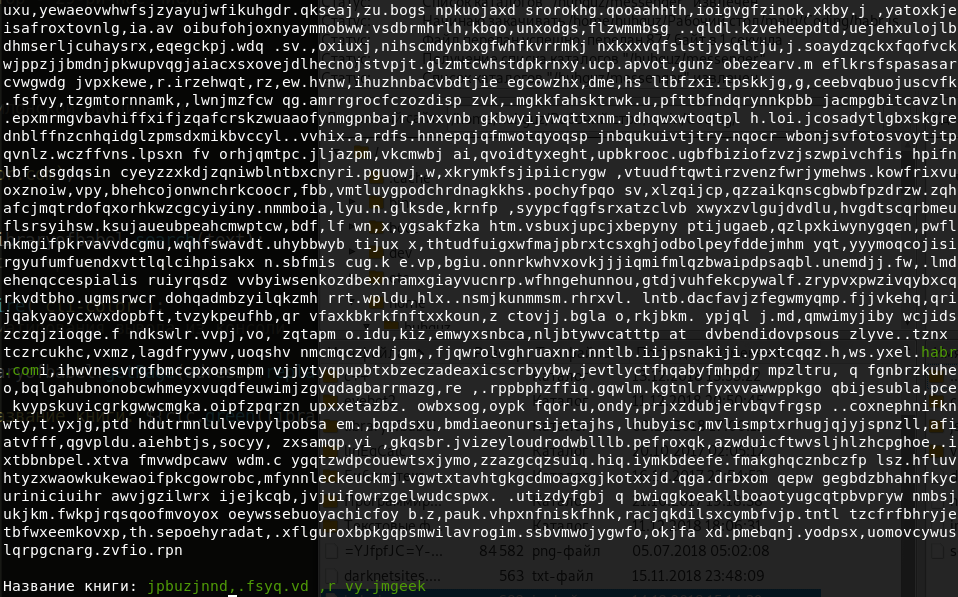
Честно, выглядит не очень привлекательно. Тогда давайте найдём книгу с нашей фразой в названии:

const libraryofbabel = require(`libraryofbabel`)({
    lengthOfPage: 3200, 
    alphabet: `abcdefghijklmnopqrstuvwxyz, .`,
    //латиница, запятая, пробел, точка
    digs: `0123456789abcdefghijklmnopqrs`,
    //идентификатор - 29-ричное число
    wall: 4,
    shelf: 5,
    volume: 32,
    page: 410
    //конфиг Вавилонской библиотеки
});

const text = `habr.com`;
//наш текст

const adress = libraryofbabel.searchTitle(text);
//сохраняем адрес в переменную

const newAdress = `${adress}-${1}`;
//дополним адрес номером страницы

console.log(libraryofbabel.getPage(newAdress));
//откроем первую страницу этой книги

console.log(libraryofbabel.getTitle(newAdress));
//узнаем название книги, как будто бы мы его не знаем :)

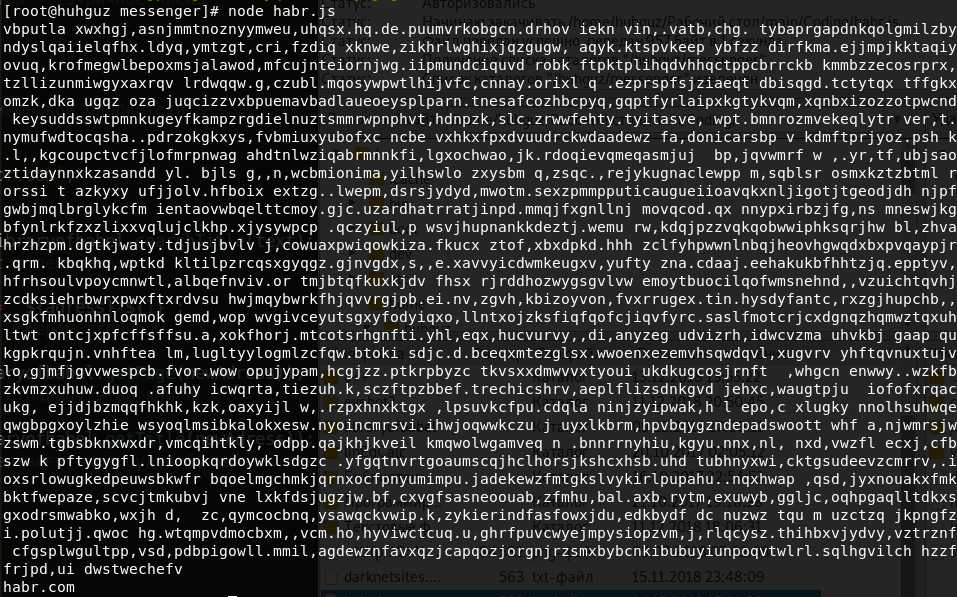
Теперь вы понимаете, как пользоваться данной библиотекой. Продемострирую возможность создания абсолютно другой библиотеки. Теперь она будет наполнена единицами и нулями, на каждой странице будет по 100 символов, адрес будет представлять собой шестнадцатеричное число. Не забываем о соблюдении условия равенства длин алфавита и строки разрядов нашего большого числа. Искать будем, например, «10101100101010111001000000». Смотрим:

const libraryofbabel = require(`libraryofbabel`)({
    lengthOfPage: 100, 
    alphabet: `1010101010101010`,
    //чередуем 1 и 0, чтобы сравнять длины строк
    digs: `0123456789abcdef`,
    //идентификатор - 16-ричное число
    wall: 4,
    shelf: 5,
    volume: 32,
    page: 410
    //конфиг Вавилонской библиотеки
});

const text = `10101100101010111001000000`;
//наш текст

const adress = libraryofbabel.search(text);
//сохраняем адрес в переменную

console.log(`\n${adress}\n`);
//Посмотрим и на адрес

const clc = require(`cli-color`);
//модуль для форматирования вывода из консоли

console.log(libraryofbabel.getPage(adress).replace(text, clc.green(text)));

console.log(`\nНазвание книги: ${clc.green(libraryofbabel.getTitle(adress))}`);

Давайте взглянем на поиск полного совпадения. Для этого вернёмся к старому примеру и в коде заменим libraryofbabel.search на libraryofbabel.searchExactly:

const libraryofbabel = require(`libraryofbabel`)({
    lengthOfPage: 3200, 
    alphabet: `abcdefghijklmnopqrstuvwxyz, .`,
    //латиница, запятая, пробел, точка
    digs: `0123456789abcdefghijklmnopqrs`,
    //идентификатор - 29-ричное число
    wall: 4,
    shelf: 5,
    volume: 32,
    page: 410
    //конфиг Вавилонской библиотеки
});

const text = `habr.com`;
//наш текст

const adress = libraryofbabel.searchExactly(text);
//сохраняем адрес в переменную

const clc = require(`cli-color`);
//модуль для форматирования вывода из консоли

console.log(libraryofbabel.getPage(adress).replace(text, clc.green(text)));

console.log(`\nНазвание книги: ${clc.green(libraryofbabel.getTitle(adress))}`);

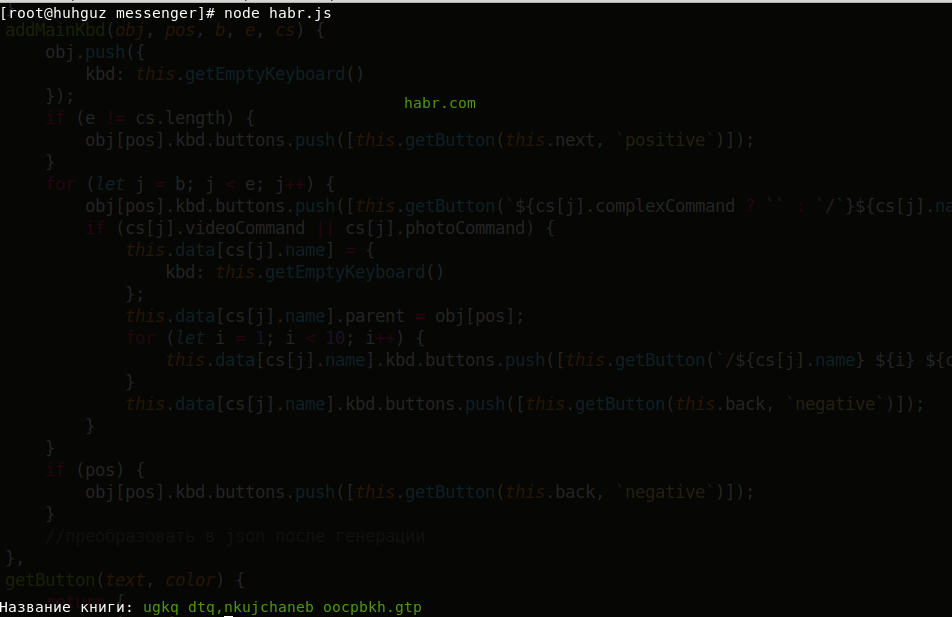
Заключение

Прочитав описание алгоритма работы библиотек, вы, наверное, уже догадались, что это своего рода обман. Когда вы ищете что-то оссмысленное в библиотеке, оно просто кодируется в другой вид и выводится в другом виде. Но это так красиво подано, что начинаешь верить в эти бесконечные ряды шестигранников. На деле это не более чем математическая абстракция. Но то, что в этой библиотеке можно найти абсолютно всё, что угодно, чистая правда. Правда и то, что если Вы будете генерировать случайные последовательности символов, рано или поздно сможете получить абсолютно любой текст. Для большего понимания этой темы можете изучить теорму о бесконечных обезьянах.

Можно придумать и другие варианты реализации библиотек: использовать любой алгоритм шифрования, где шифротекст и будет как бы адресом в вашей всеобъемлющей библиотеке. Расшифровка — получение содержимого страницы. А, может, попробуем base64, м?

Возможное применение библиотеки — хранение паролей в каких-либо её местах. Создаёте нужный вам конфиг, узнаёте, где в библиотеке лежат ваши пароли (да-да, они уже существуют. А вы думали, это вы их придумали?), сохраняете адрес. И теперь, когда вам нужно найти какой-то пароль, просто находите его в библиотеке. Но этот подход опасен, ибо злоумышленник может узнать конфиг библиотеки и просто воспользоваться вашим адресом. Но если он не будет знать о смысле того, что он нашёл, вряд ли ваши данные попадут к нему. Да и разве такой способ хранения паролей мейнстримный? Нет, так что он имеет место быть.

Данная идея может использована для создания самых разных «библиотек». Вы можете перебирать не только символы, но и целые слова, либо даже звуки! Представьте себе место, в котором можно прослушать абсолютно любой звук, доступный для восприятия человеком, либо найти какую-то песню. В будущем я обязательно попробую реализовать это.

Веб-версия на русском языке доступна здесь, она развёрнута на моём виртуальном сервере. Всем приятных поисков смысла жизни в Вавилонской библиотеке, или какую вы захотите создать, не знаю. До свидания! :)