В своей предыдущей статье я рассказывал, как я делал анимацию планет Солнечной системы для своего сына. Спасибо всем за оставленные там отзывы и «теплый» прием. Сегодня я подготовил еще несколько интересных анимаций, условно объединенных под тему «круговое движение и колебания». Другими словами, то, что описывается с помощью косинусов и синусов.

Для отрисовки я использовал javascript и canvas. Для каждого примера дана ссылка, где вы можете всё внимательно посмотреть. Можно заглядывать в исходный код, можно копировать себе — я не буду возражать. Материал вполне может пригодиться на занятиях и факультативах по физике, математике или информатике.
Итак, поехали.
Траектория Луны
Давайте начнем с небесной механики. Мой любимый вопрос для школьников: «Земля движется [почти] по кругу вокруг Солнца, а Луна — по кругу вокруг Земли. Как выглядит траектория Луны в системе отсчета Солнца?» Я надеюсь, что уважаемые читатели окажутся более подготовленными и не начнут рисовать подобные «завитушки»:
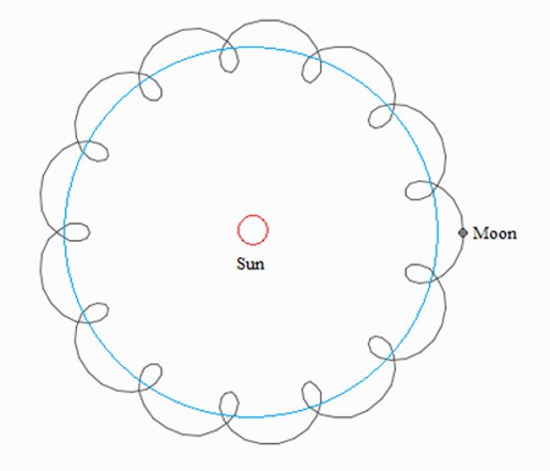
Хотя такая траектория и подходит под здравый смысл, но конкретно с Луной так не бывает. На самом деле, Земля «несется» по орбите, а Луна, как привязанная, оказывается то слегка слева, то слегка справа. Действительно: орбитальная скорость Земли ~30 км/с, Луны — примерно 1 км/с. Очевидно, что скорости Луны никак не хватает, чтобы она могла двигаться в противоположную сторону. Более точное объяснение связано с расчетом действующих на Луну сил (со стороны Земли и Солнца) и того, куда направлен радиус кривизны траектории (оставлю это на самостоятельное изучение).
Итак, по теории вроде бы понятно. Но всё равно остается некоторая недосказанность. Хочется посмотреть, как оно есть на самом деле. Давайте сделаем модель в масштабе 1 пиксель = 30000 км. Это компромиссный вариант, чтобы орбиты были различимы, хотя масштаб картинки все равно получается огромным: 15000*15000 пикселей. На анимации движение Земли и Луны описывается законами кругового движения: голубая траектория для Земли, и черная для Луны. Сделав отрисовку, можно посмотреть на итог. Видно, насколько малы общие отклонения орбиты Луны от орбиты Земли. Вот для примера малый фрагмент картинки:

Так что имеющие в интернете рисунки крайне искажены, нужно об этом помнить.
Кстати, ради интереса можно сделать такую же анимацию с каким-нибудь спутником Юпитера. По идее, там уже должны получаться «завитушки».
Фигуры Лиссажу
Когда-то давно, когда я учился в новосибирской физматшколе, у нас была лабораторная работа «Фигуры Лиссажу», как и положено, с генераторами и советским осциллографом. Выглядело это основательно и интересно. В зависимости от частот сигналов, подаваемых на входы, на экране осциллографа получаются различные фигуры:
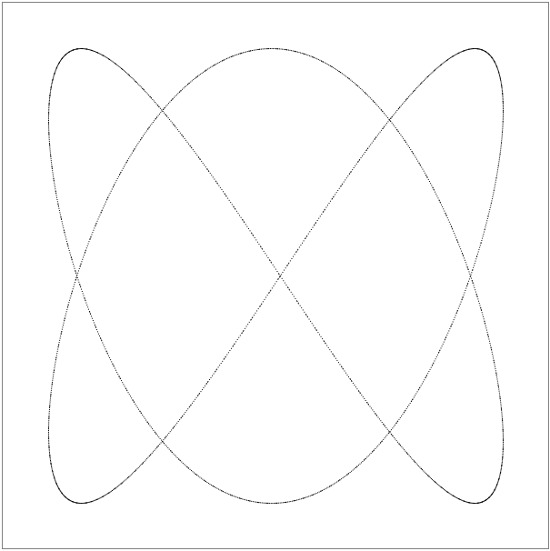
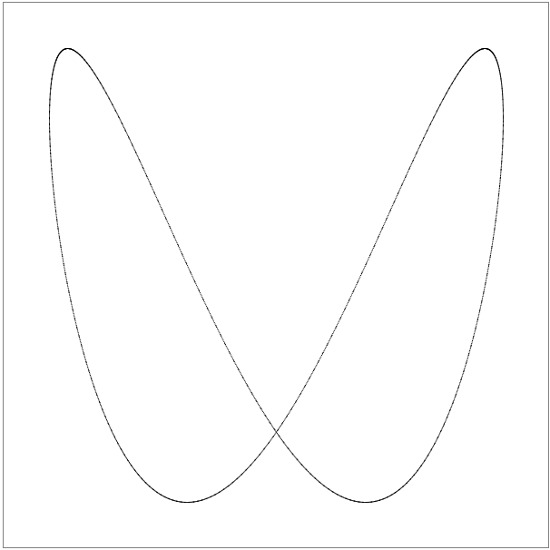
По сути, каждая фигура представляет собой сложение двух одновременных колебаний — по оси X и по оси Y. Частоты этих колебаний могут соотноситься как 1:1 (одно колебание по X, одно по Y; могут получаться окружность, эллипс или прямая), 1:2 (одно по X, два по Y; получаются парабола или «седло»), 1:3, 2:3 (более сложные фигуры) и так далее — думаю, принцип вы поняли. Подробную теоретическую основу вы можете найти в Википедии, а я подготовил отдельную страницу, где можно «поиграться» с разными коэффициентами.
Интересным параметром является сдвиг фазы между колебаниями. Если его непрерывно менять, то фигура «оживает» — начинает вращаться. Здесь моим любимым вопросом является такой: «а в какую сторону она вращается?» Кто-то говорит, что в одну сторону, кто-то — что в другую, а вообще можно «переключать» направление вращения прямо на ходу. Это чисто вопрос восприятия. Попробуйте и вы так сделать.
Усложним нашу анимацию, добавив в нее еще и затухание. В этом случае точка постепенно «падает» в центр, но, опять же, по замысловатой и довольно красивой траектории.

Кстати, подобное можно сделать и вживую. Как советуют в одной книге, нужно сделать цилиндр с малым отверстием внизу, насыпать туда манки, подвесить в дверной проем и качнуть. Высыпающася манка как раз и будет рисовать затухающую фигуру Лиссажу.
Спирограф
Игрушка из детских воспоминаний, когда я, будучи в возрасте 6-7 лет, рисовал узоры в гостях у бабушки:

Если вдруг кто-то, по какому-то неслыханному стечению обстоятельств, не знаком с этим чудом, то бегом в Википедию. Мы же посмотрим на страницу с анимацией. Параметров, как и в реальном спирографе, всего три: радиусы малого/большого круга и расстояние от точки до центра малого круга. Но их разные комбинации дают огромное количество узоров (примеры вы видели в начале этой статьи).
Кстати, у скрипта обнаружилась одна интересная особенность: в нем можно задавать такие комбинации, которые в реальном спирографе просто невозможны – например, сделать внутренний круг больше внешнего, или вообще вынести отверстие за пределы внутреннего круга. Программа позволяет придумывать всё, что угодно.
Результаты
Давайте подведем итог. Как видите, наши анимации находятся на стыке физики и информатики. Хорошо и интересно прочитать про Луну или те же фигуры Лиссажу, но вдвойне хорошо и интересно — увидеть это на экране и «поиграться» с параметрами. Конечно, если есть реальные объекты для получения результата, то, разумеется, нужно пользоваться им (например, электронные приборы — генераторы, осциллограф — для наблюдения фигур Лиссажу). Я вообще сторонник «работать руками». Но часто нет ничего подходящего — в таких случаях выручает анимация на компьютере.
Еще я хотел бы отдельно отметить эстетическую составляющую. Природа, по моему личному убеждению, невероятно красива в своей сути. Согласитесь, приятно смотреть на короткую и простую формулу, которая описывает целый класс явлений. Или, опять же, на графическое представление какой-то формулы (как со спирографом). А, например, силовые линии магнитного поля? А результат столкновения частиц? Помню, в университете мы тоже рисовали решения дифференциальных уравнений — даже там были свои изящество и красота. Если вы всё это знаете и понимаете, о чем я говорю — давайте пожмем друг другу руки. А если вы только сейчас заинтересовались этим — для вас всё только начинается. Сегодня был первый шаг.
Комментарии (22)

GeMir
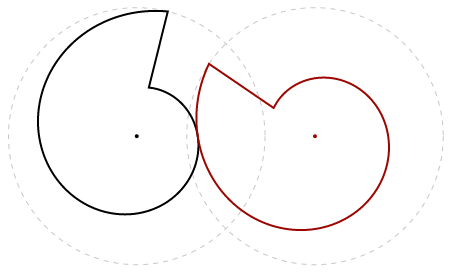
24.12.2018 00:46Для интересующихся спиралями — поищите «колёса Рёмера» (Romer-Rader):

vashu1
24.12.2018 07:28Поиск «колёса Рёмера» выдает лишь зубчатое колесо которым пользовались для измерения скорости света(не Ремер, но в тех же статьях и он упоминается).
Не уточните, что за колеса такие?
GeMir
24.12.2018 11:50Две логарифмические «спирали» катящиеся по поверхностям друг-друга. Расстояние между центрами спиралей остаётся постоянным. Конструкция, изобретённая Рёмером для того, чтобы создавать вращение с изменяемой угловой скоростью (Zwikker, C.: The Advanced Geometry of Plane Curves and Their Apprications. Dover Publications, New York, 1963.).
Давно-давно рисовал небольшое демо (извиняюсь за «качество» кода).

sim31r
24.12.2018 02:29Была хабре тема про гильоши, с примерами алгоритмов подобных.
Я там в комментариях свой пример представил.
Согласитесь, приятно смотреть на короткую и простую формулу, которая описывает целый класс явлений.
У фракталов то же самое.

Germanjon
24.12.2018 07:22В своё время на C# рисовал циклоиды, эпициклоиды — было интересно и красиво. Ещё рекомендую попробовать ситуацию, когда второе колесо «катится» по внешней стороне первого колеса (у спирографа — по внутренней).

druzhkov Автор
24.12.2018 07:40когда второе колесо «катится» по внешней стороне первого колеса
Я пробовал такой трюк на живом спирографе, у него в наборе как раз три колеса. Получается волнистая линия, но не более того.
Germanjon
24.12.2018 11:53+1Оказывается, я имел в виду «Эпициклоиду». При разных отношениях радиусов «колёс» могут получиться и красивые фигурки.

Опять-таки, в случае с программированием, можно взять точку не на поверхности второго колеса, а внутри или снаружи него.
druzhkov Автор
24.12.2018 13:14Точно, спасибо. Я попробовал с реальными шестеренками и больше не стал думать в этом направлении. Действительно, в программе же можно вынести точку за пределы колеса.

mwambanatanga
24.12.2018 08:03Прочитал про интуитивную и фактическую траекторию движения Луны и задумался, как же должен выглядеть «спирограф», которых мог бы её нарисовать. По идее, вокруг большого круга (с Солнцем в центре) должен вращаться круг поменьше (с Землёй в центре). Чтобы малый круг сделал [примерно] 12 оборотов вокруг большого, окужности (а значит и диаметры) кругов должны соотноситься как 1:12. При этом Луна будет точкой на малом круге, но не на краю, как обычно, а очень близко от центра (т.е. от Земли). Такой спирограф будет рисовать очень скучную, но реалистичную траекторию.
P.S.: Или, наоборот, малый круг должен вращаться внутри большого? :-)

Occama
24.12.2018 14:22А вот в последнем абзаце уже диалектика, природа ли красива, или наши понятия красоты продиктованы природой =)



Tantrido
Рисовал такое на Бейсике на БК-0010 :)
SystemXFiles
Я именно с этих фигур начинал программировать, тоже на basic, только под dos в эмуляторе)
tegArt
Было дело на spectrum 48k :)
Tantrido
Да ты крутой был! На БК-0010 было 16К :)
tegArt
Так-себе крутость для конца 90-х, пеньки уже вовсю в ходу были :)
Tantrido
В конце 90-х и у меня пенёк уже был :) А в 89-91 — БК.