Что может быть более загадочным, чем взаимодействие мнимых чисел с вещественными, в результате дающее ничто? Такой вопрос задал читатель журнала Physics World в 2004 году, чтобы подчеркнуть красоту уравнения Эйлера «e в степени i, умноженного на пи равно минус единице».
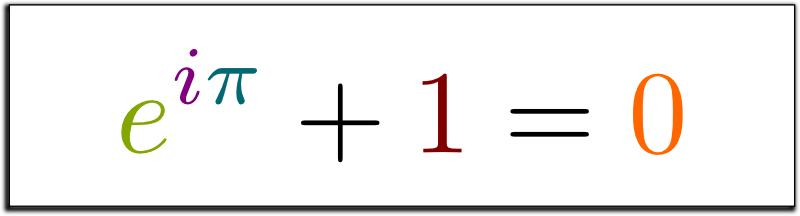
Рисунок 1.0: тождество Эйлера — e в степени i, умноженного на пи, плюс единица равно нулю.
Ещё раньше, в 1988 году, математик Дэвид Уэллс, писавший статьи для американского математического журнала The Mathematical Intelligencer, составил список из 24 теорем математики и провёл опрос, попросив читателей своей статьи выбрать самую красивую теорему. И после того, как с большим отрывом в нём выиграло уравнение Эйлера, оно получило званием «самого красивого уравнения в математике».
Рисунок 2.0: обложка журнала The Mathematical Intelligencer
Рисунок 3.0: опрос Дэвида Уэллса из журнала
Леонарда Эйлера называют самым продуктивным математиком за всю историю. Других выдающихся математиков вдохновляли его работы. Один из лучших физиков в мире, Ричард Фейнман, в своих знаменитых лекциях по физике назвал уравнение Эйлера «самой примечательной формулой в математике». Ещё один потрясающий математик, Майкл Атья, назвал эту формулу "…математическим аналогом фразы Гамлета — «быть или не быть» — очень короткой, очень сжатой, и в то же время очень глубокой".
Существует множество интересных фактов об уравнении Эйлера. Например, оно встречалось в некоторых эпизодах «Симпсонов».
Рисунок 4.0: в этой сцене уравнение Эйлера можно заметить на второй книге в самой правой стопке.
Рисунок 5.0: в этой сцене уравнение Эйлера написано на футболке второстепенного персонажа.
Также уравнение Эйлера стало ключевым пунктом в уголовном деле. В 2003 году аспирант Калифорнийского технологического института Билли Коттрелл писал краской на чужих спортивных автомобилях уравнение Эйлера. На суде он сказал: "Я знал теорему Эйлера с пяти лет, и её обязаны знать все".
Рисунок 6.0: купюра, выпущенная в 1983 году в Германии в память о двухсотлетии со смерти Эйлера.
Рисунок 7.0: марка, выпущенная Швейцарией в 1957 году в честь 250-й годовщины Эйлера.
Почему уравнение Эйлера так важно?
Вы имеете полное право задаться вопросом: почему Билли Коттрелл считал, что об уравнении Эйлера обязаны знать все? И был настолько в этом уверен, что начал писать его на чужих машинах? Ответ прост: Эйлер воспользовался тремя фундаментальными константами математики и применил математические операции умножения и возведения в степень, чтобы записать красивую формулу, дающую в результате ноль или минус один.
- Константа e связана со степенными функциями.
- Константа i является не вещественным, а мнимым числом, равным квадратному корню из минус единицы.
- Знаменитая константа ? (пи) связана с окружностями.
Впервые тождество Эйлера появилось в 1748 году в его книге Introductio in analysin infinitorum. Позже другие люди увидели, что эта формула связана с тригонометрическими функциями синуса и косинуса, и эта связь удивительна, ведь степенная функция стремится к бесконечности, а тригонометрические функции колеблются в интервале от — 1 до -1.
e в степени i, умноженного на ? (phi) = cos ? (phi) + sin ? (phi)
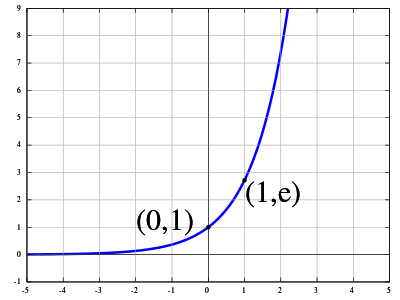
Рисунок 8.0: экспоненциальная функция y=ex.
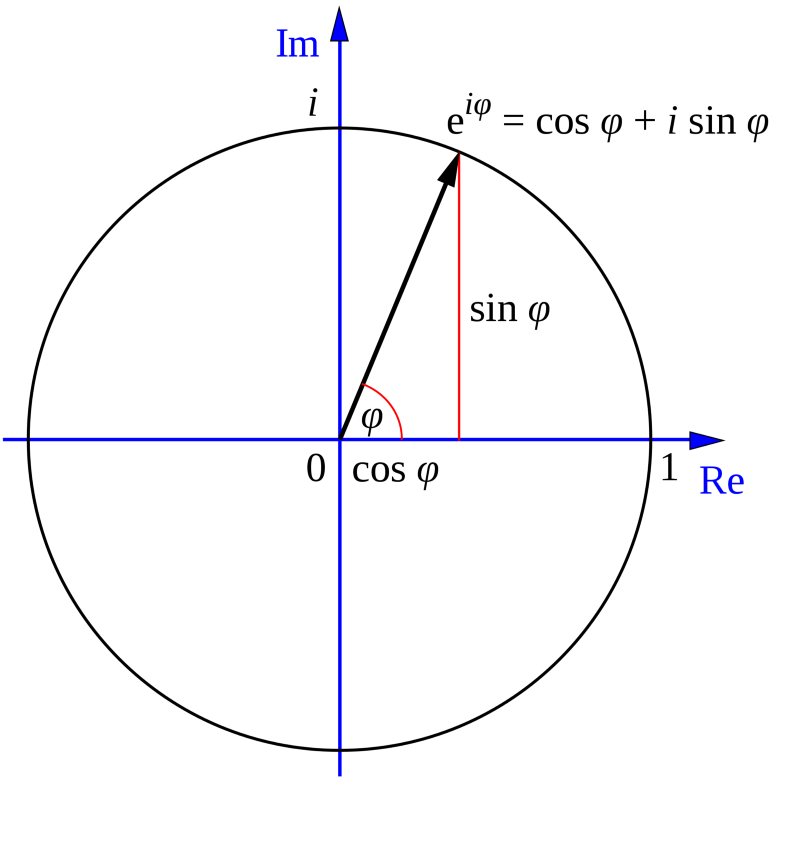
Рисунок 8.1: график тождества Эйлера.
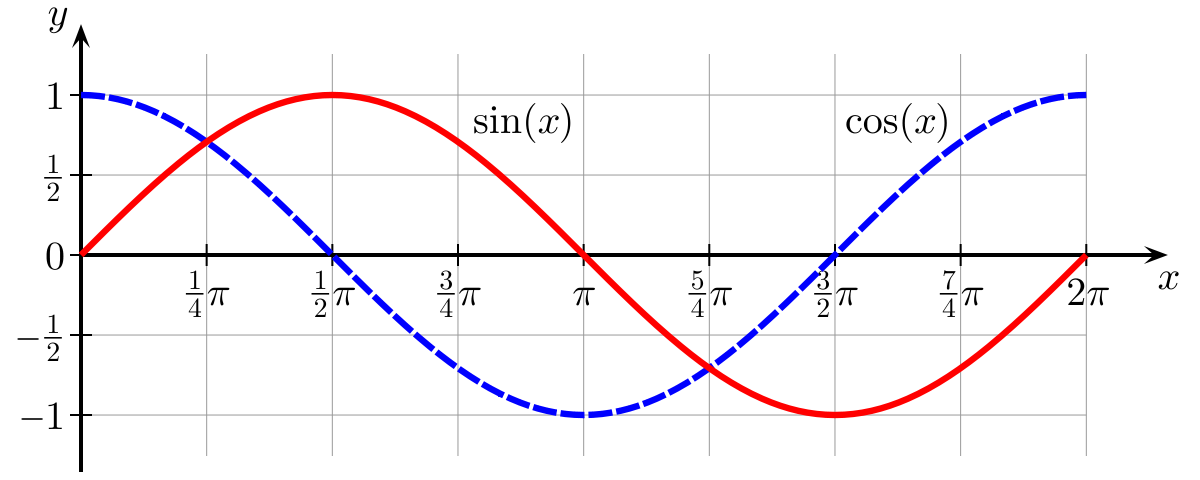
Рисунок 8.2: частоты, испускаемые LC-цепью.
Показанные выше уравнения и графы могут показаться абстрактными, но они важны для квантовой физики и вычислений обработки изображений, и при этом зависят от тождества Эйлера.
1: число для счёта
Число 1 (единица) является основой нашей системы исчисления. С неё мы начинаем счёт. Но как мы считаем? Чтобы считать, мы используем цифры 0–9 и систему разрядов, определяющую значение цифры.
Например, число 323 означает 3 сотни, 2 десятка и 3 единицы. Здесь число 3 исполняет две разные роли, которые зависят от его расположения.
323 = (3*100) + (2*10) + (3*1)
Существует и другая система исчисления, называемая двоичной. В этой системе вместо 1 используется основание 2. Она широко применяется в компьютерах и программировании. Например, в двоичной системе:
1001 = (23) + (02) + (01) + (20) = [9 в системе с основанием 10]
Кто создал системы исчисления? Как первые люди считали предметы или животных?
Как возникли наши системы исчисления? Как считали первые цивилизации? Мы точно знаем, что они не пользовались нашей разрядной системой. Например 4000 лет назад древние египтяне использовали систему исчисления с разными символами. Однако они комбинировали символы, создавая новый символ, обозначающий числа.
Рисунок 11: показанные здесь иероглифы образуют число 4622; это одно из чисел, вырезанных на стене в храме в Карнаке (Египет).
Рисунок 12: иероглифы — это изображения, обозначающие слова, а в данном случае — числа.
В то же время, но в другом месте ещё один социум обнаружил способ подсчёта, но в нём тоже использовались символы. Кроме того, основанием их системы исчисления было 60, а не 10. Мы используем их метод счёта для определения времени; поэтому в минуте 60 секунд, а в часе 60 минут.
Рисунок 13: вавилонские числа из шестидесятиричной системы счисления (с основанием 60).
Тысячу лет спустя древние римляне изобрели римские числа. Для обозначения чисел они использовали буквы. Римская нотация не считается разрядной системой, потому что для многих значений нашей системы счисления в ней использовались разные буквы. Именно по этой причине для счёта они использовали абакус.
Рисунок 14: романский абакус в шестнадцатеричной (с основанием 16) системе счисления
Рисунок 15: таблица преобразования из арабских в римские числа
Древние греки тоже не использовали разрядную систему счисления. Греческие математики обозначали числа буквами. У них были специальные буквы для чисел от 100 до 900. Многие люди в то время считали греческие числа запутанными.
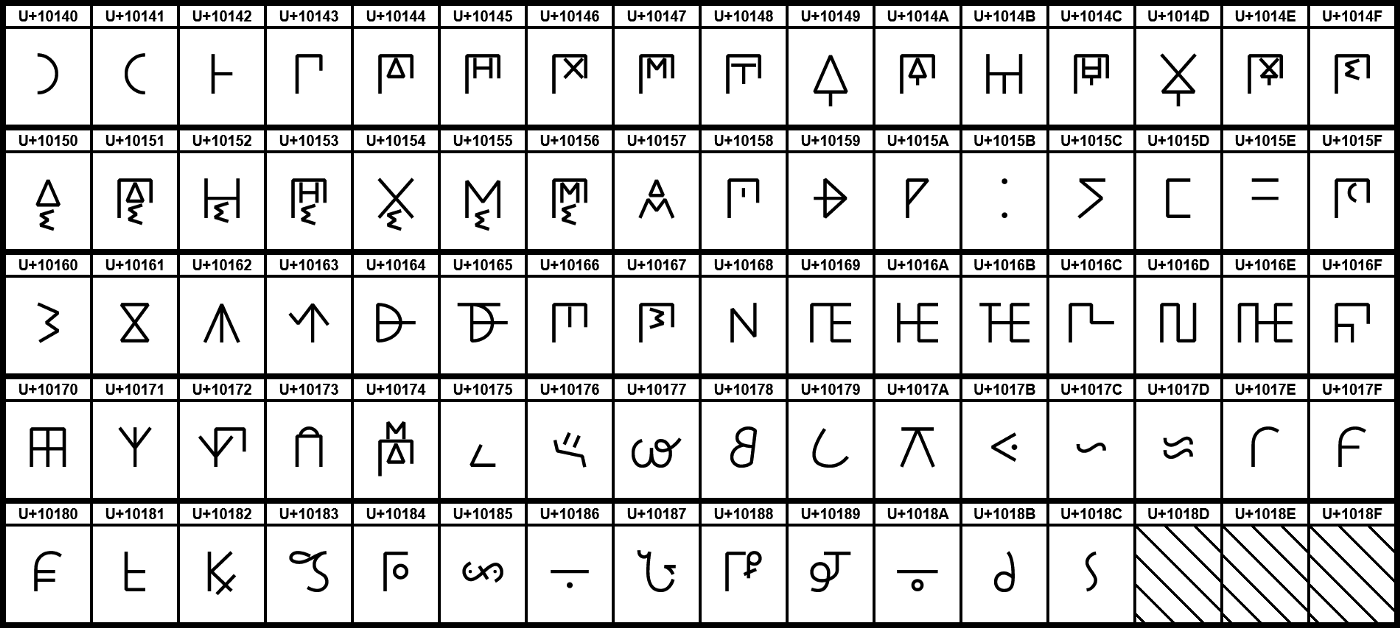
Рисунок 15: таблица букв древних греков.
В то же самое время китайские математики начали использовать для расчётов небольшие бамбуковые палочки. Этот китайский способ счёта называют первой десятичной разрядной системой.
Рисунок 16: китайский способ счёта с числами-палочками. Использовался как минимум с 400 года до нашей эры. Квадратная счётная доска использовалась примерно до 1500 года, когда её заменил абакус.
Однако самая уникальная система счёта использовалась индейцами майя. Их система счисления имела основание 20. Для обозначения чисел от 1 до 19 они использовали точки и линии. Чем же отличалась их система счисления? Для каждого числа они использовали изображения голов и отдельный символ нуля 0.
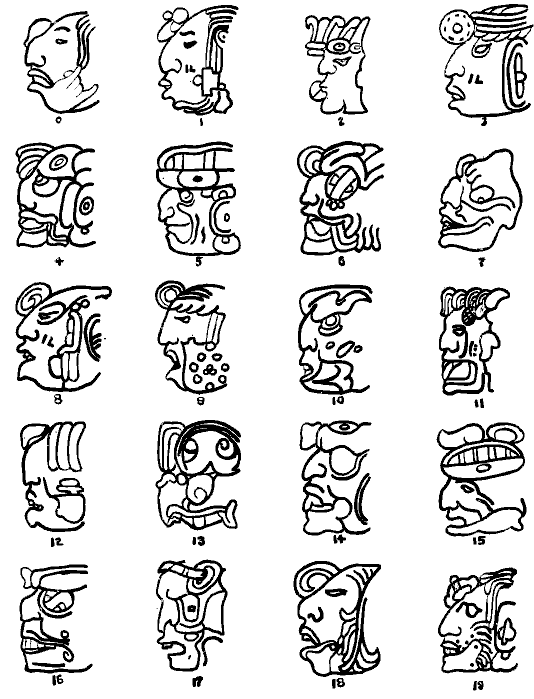
Рисунок 17: Система счисления майя с основанием 20, в которой числа обозначались головами
Рисунок 18: ещё один способ записи чисел майя.
0: число для обозначения ничего
Некоторые цивилизации использовали пробелы, чтобы, например, отличать число 101 от 11. Спустя какое-то время начало появляться особое число — ноль. К примеру, в пещере в индийском городе Гвалиор археологи обнаружили на стене число 270, в котором был ноль. Самое первое зафиксированное использование нуля можно увидеть в Бодлианской библиотеке.
Рисунок 19: вырезанный на стене храма в Гвалиоре круг обозначает ноль. Ему примерно 1500 лет.
Рисунок 20: чёрные точки в манускрипте Бакхшали обозначают нули; это самый старый письменный пример использования числа, ему примерно 1800 лет.
Примерно 1400 лет назад были записаны правила вычислений с нулём. Например, при сложении отрицательного числа и нуля получается то же отрицательное число. Деление на нуль не допускается, потому что если разделить на ноль, то мы получим число, которое может быть равно любому нужному нам числу, что должно быть запрещено.
Вскоре после этого многими людьми были опубликованы книги по арифметике, распространяющие использование индо-арабской записи чисел. Ниже показана эволюция индо-арабских чисел. В большинстве стран используется индо-арабская система чисел, но арабские страны до сих пор пользуются арабскими числами.
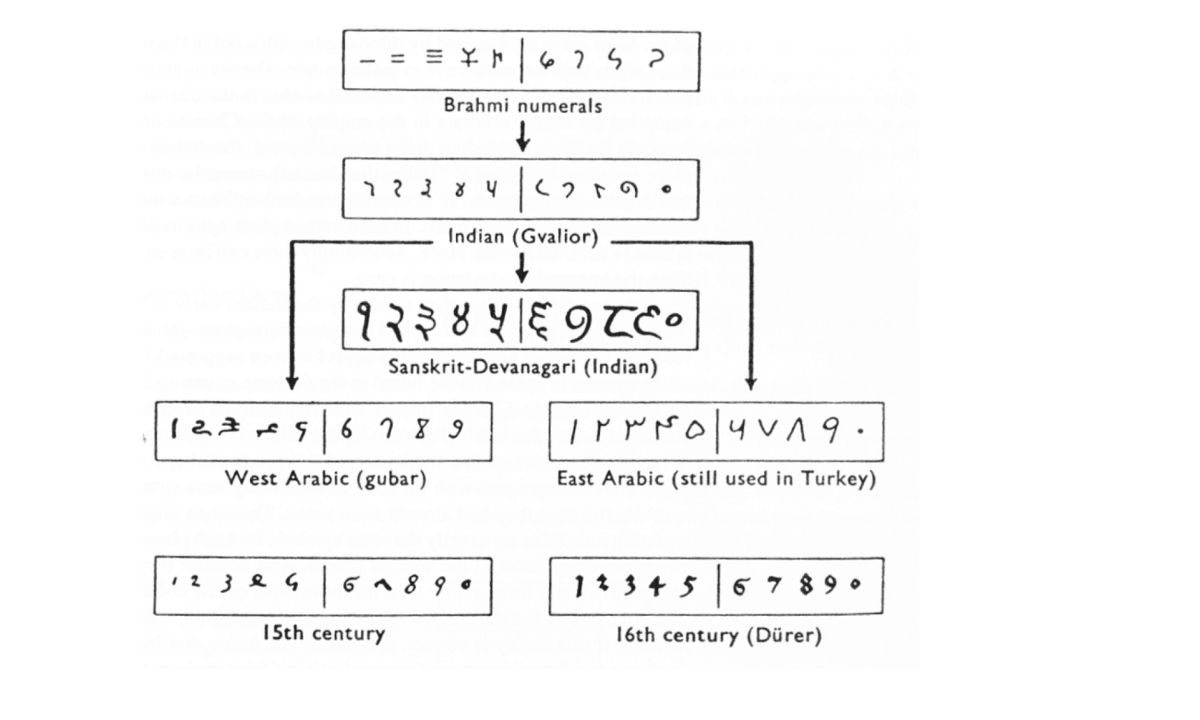
Рисунок 21: на этой схеме показана эволюция чисел, происходящих от чисел брахми и заканчивающаяся числами, которыми мы используем и сегодня.
Рисунок 22: классическая гравюра «Арифметика» из Margarita Philosophica Грегора Рейша, на которой изображено соревнование между Боэцием, улыбающимся после открытия индо-арабских чисел и письменных вычислений, и нахмуренным Пифагором, до сих пор пытающимся пользоваться счётной доской.
Пи (?): самое известное иррациональное число
Пи — самое популярное из известных нам иррациональных чисел. Пи можно найти двумя способами: вычислив соотношение длины окружности к её диаметру, или соотношение площади круга к квадрату его радиуса. Евклид доказал, что эти соотношения постоянны для всех окружностей, даже для луны, пенни, шины и т.д.
? = окружность / диаметр ИЛИ ? = площадь круга / радиус?
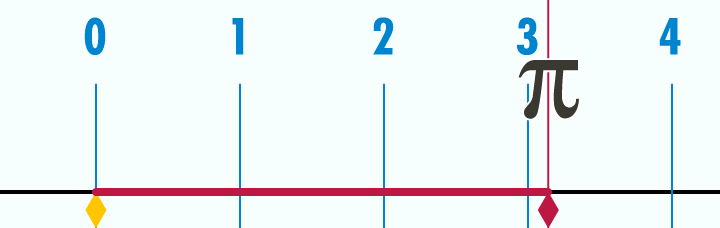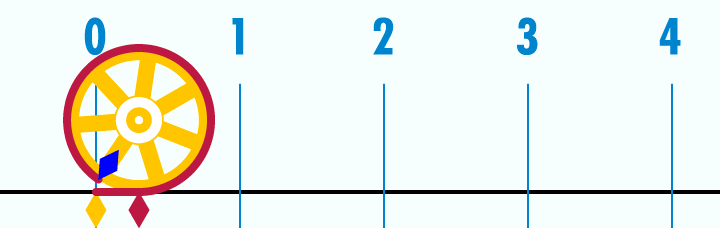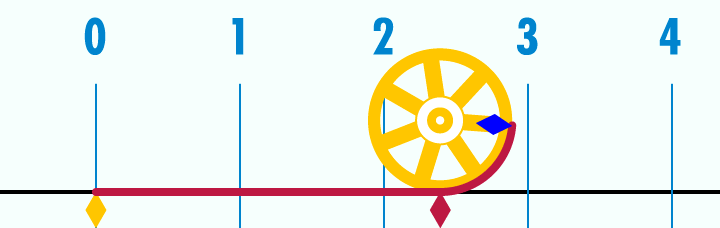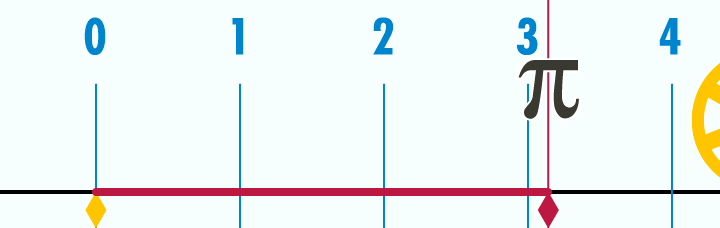
Рисунок 22: анимированная связь между окружностью и диаметром в отношении пи.
Так как иррациональные числа наподобие пи бесконечны и не имеют повторений, мы никогда не закончим записывать пи. Оно продолжается вечно. Есть люди, запомнившие множество десятичных разрядов пи (нынешний рекорд — 70 000 цифр! Источник: «Книга рекордов Гиннесса» ).
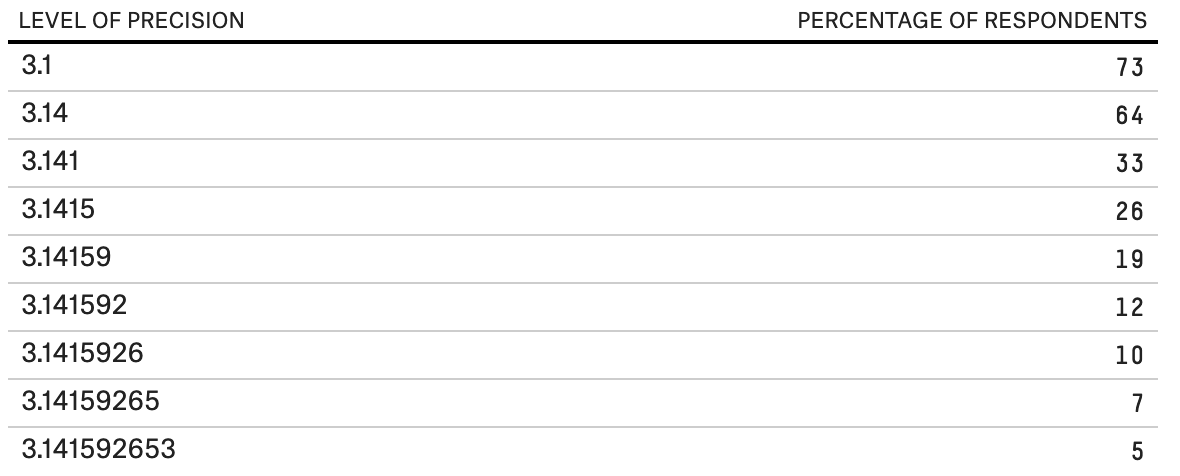
Рисунок 23: данные опроса 941 респондентов для определения процента людей, способных запомнить знаки пи после запятой.
Рисунок 24: На стене станции метро Karlsplatz в Вене записаны сотни разрядов пи.
На данный момент компьютеры смогли вычислить всего 2,7 триллиона разрядов пи. Может казаться, что это много, но на самом деле этот путь бесконечен.
Как я сказал выше, число пи нашёл Евклид. Но как поступали люди до Евклида, когда им нужно было найти площадь круга? Историки обнаружили вавилонскую глиняную табличку, в которой было записано отношение периметра шестиугольника к длине описанной вокруг него окружности. После вычислений полученное число оказалось равным 3.125. Это очень близко к пи.
Рисунок 24: вавилонская глиняная табличка с отношением периметра шестигольника к длине описанной окружности.
Рисунок 25: Numberwarrior
Древние египтяне тоже близко подобрались к значению пи. Историки обнаружили документ, показывающий, как древние египтяне нашли число пи. Когда историки перевели документ, то нашли такую задачу:
Например, чтобы найти площадь поля диаметром 9 хета (1 хет = 52,35 метра), нужно выполнить следующее вычисление:
Вычесть 1/9 диаметра, а именно 1. Остаток равен 8. Умножить его на 8, что даёт нам 64. Следовательно, площадь будет равна 64 setjat (единица измерения площади).
Другими словами, диаметр равен 2r, а 1/9 радиуса равно (1/9 • 2r). Тогда если мы вычтем это из исходного диаметра, то получим 2r?—?(1/9 • 2r) = 8/9(2r). Тогда площадь круга равна 256/81 r?. То есть пи равно почти 3,16. Они обнаружили это значение пи примерно 4000 лет назад.
Рисунок 26: математический папирус Ахмеса.
Однако греческие математики нашли для вычисления пи способ получше. Например, Архимед предпочитал работать с периметрами. Он начал рисовать окружности, описывающие многоугольники разного размера. Когда он чертил шестиугольник, то рисовал окружность с диаметром 1. Затем он видел что каждая сторона шестиугольника равна 1/2, а периметр шестиугольника равен 1/2 x 6 = 3. Затем он увеличивал количество сторон многоугольника, пока он не становился похожим на круг. Работая со 96-сторонним многоугольником и применив тот же способ, он получил 2 десятичных разряда пи после запятой: 3 и 10/71 = 3,14084. Спустя много лет китайский математик Лю Ху использовал 3072-сторонний многоугольник и получил число 3,14159 (5 верных десятичных разряда пи после запятой). После этого ещё один китайский математик Цзу Чунчжи провёл ещё более впечатляющую работу. Он работал со 24000-сторонним многоугольником и получил 3,1415926 — семь верных десятичных разрядов пи после запятой.
Спустя тысячу лет немецкий математик Людольф Цейлен работал со 262-сторонним многоугольником и получил 35 десятичных разрядов пи. Это число, названное Людольфовым, было высечено на его могильном камне.
В 1706 году англичанин Джон Мэчин, долгое время работавший профессором астрономии, использовал формулу сложения, чтобы доказать, что пи равно
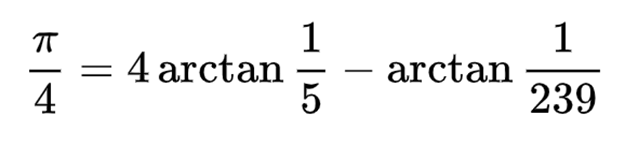
Не беспокоясь о том, как откуда взялась эта формула, Мэчин начал постоянно ею пользоваться, а затем записал показанный ниже ряд. Это был самый большой на то время шаг в количестве разрядов пи.
Рисунок 29: Формула Мэчина для пи
Однако первое упоминание пи появилось в 1706 году. Преподаватель математики Уильям Джонс написал книгу и впервые предложил пи для измерения окружностей. Так пи впервые появилась в книгах!
Рисунок 30: Juliabloggers
В 1873 году Уильям Шэнкс воспользовался формулой Джона Мэчина и получил 707 десятичных разрядов пи. Эти цифры написаны в комнате пи парижского Дворца открытий. Однако позже математики выяснили, что верными являются только 527 разрядов.
Рисунок 31: комната пи
С другой стороны, более интересный способ нахождения пи обнаружил Буффон. Его эксперимент основывался на случайном разбрасывании иголок для оценки пи. Он нарисовал на доске несколько параллельных линий на расстоянии D и взял иголки длиной L. Затем он случайным образом начал бросать иголки на доску и записывал долю иголок, пересекавших линию.
Рисунок 32: Science Friday
А после этого другой математик по имени Ладзарини подбросил иголку 3408 раз и получил шесть десятичных разрядов пи с соотношением 355/113. Однако если бы одна иголка не пересекла линию, он получил бы только 2 разряда пи.
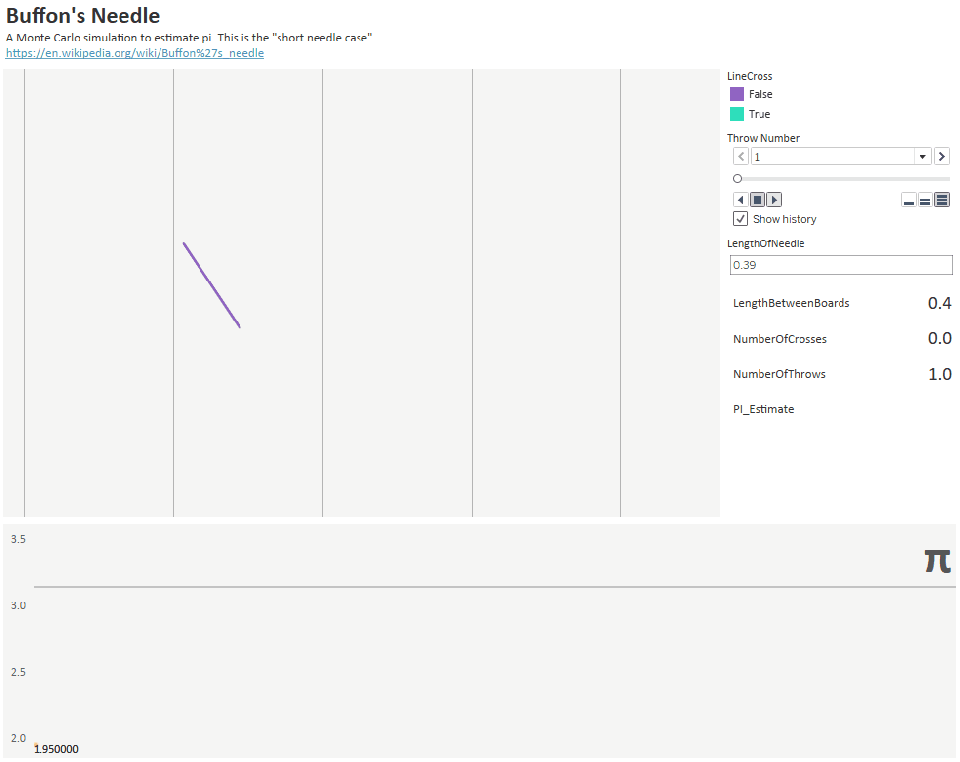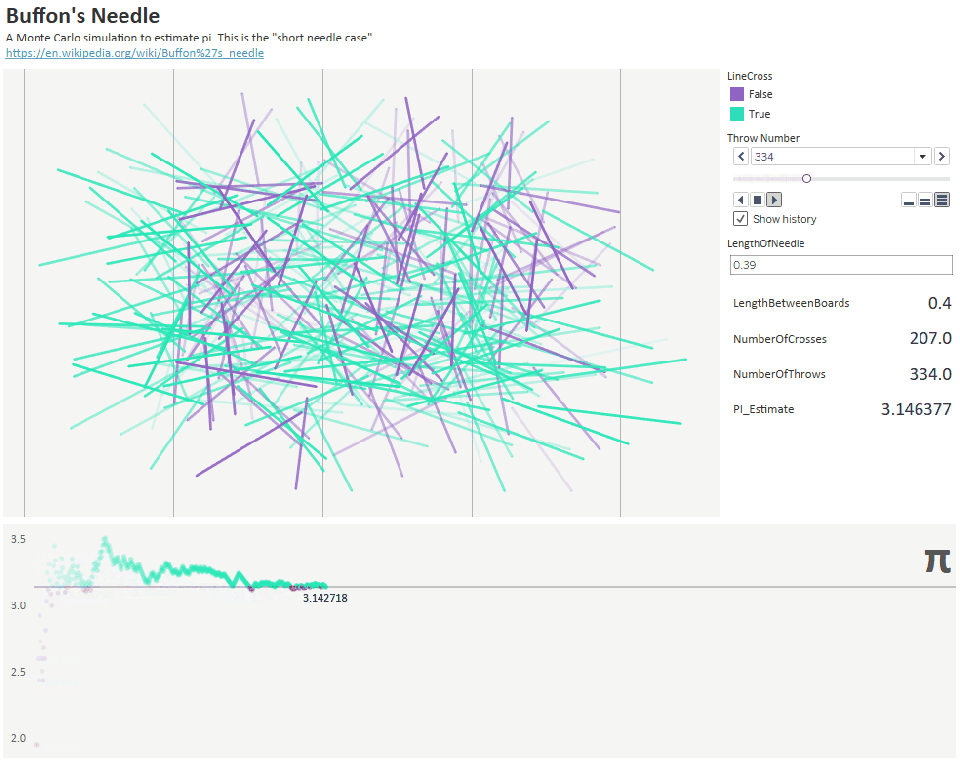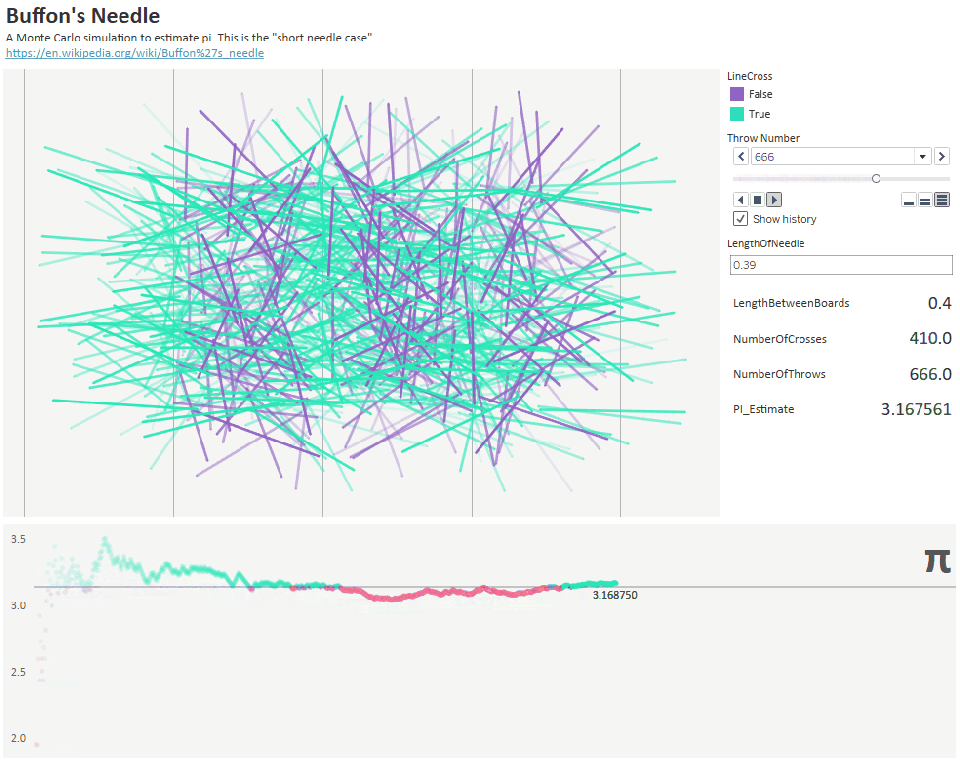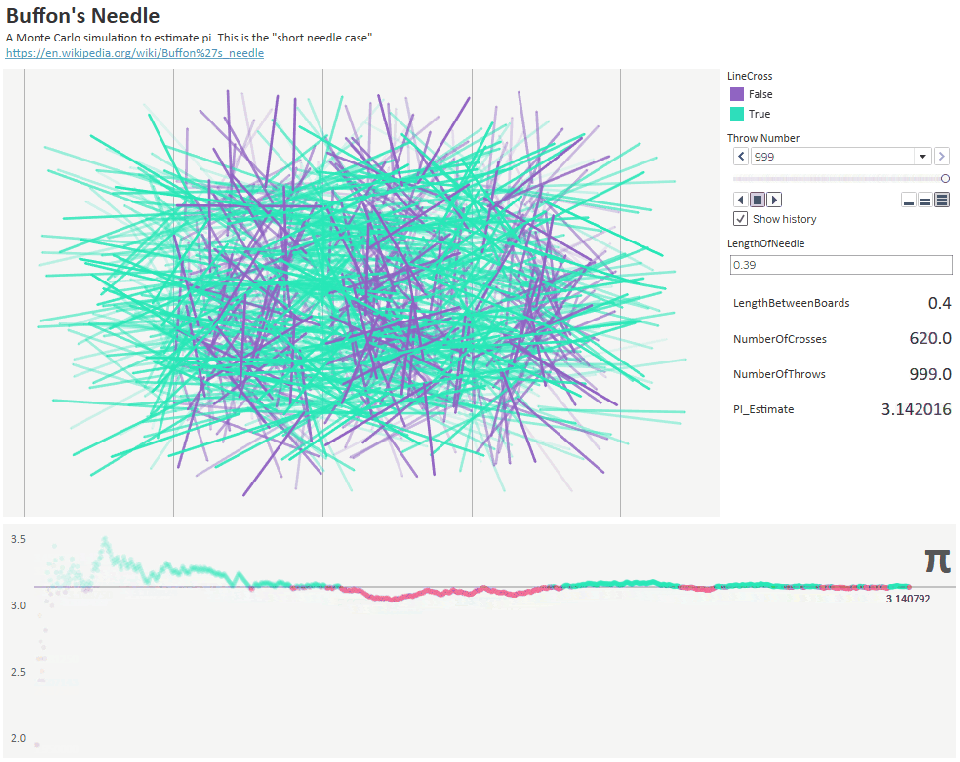
Рисунок 32: бросание 1000 иголок для оценки приблизительного значения пи
e: история экспоненциального роста
e — это ещё одно знаменитое иррациональное число. Дробная часть e тоже бесконечна, как и у пи. Мы используем число e для вычисления степенного (экспоненциального) роста. Другими словами, мы используем e, когда видим очень быстрый рост или уменьшение.
Один из величайших, а возможно и лучший математик Леонард Эйлер открыл число e в 1736 году и впервые упомянул это особое число в своей книге Mechanica.
Рисунок 33: источник
Чтобы разобраться в экспоненциальном росте, мы можем использовать историю об изобретателе шахмат. Когда он придумал эту игру, то показал её властителю Севера. Царю понравилась игра и он пообещал, что отдаст автору любую награду. Тогда изобретатель попросил нечто очень простое: 20 зерна на первую клетку шахматной доски, 21 зерна на вторую клетку доски, 22 зерна — на третью, и так далее. Каждый раз количество зерна удваивалось. Царь Севера подумал, что просьбу будет выполнить легко, но он ошибался, потому то на последнюю клетку нужно было бы положить 263 зёрен, что равно 9 223 372 036 854 775 808. Это и есть экспоненциальный рост. Он начался с 1, постоянно удваивался, и через 64 шага вырос в огромное число!
Если бы изобретатель шахмат выбрал линейное уравнение, например 2n, то получил бы 2, 4, 6, 8, … 128… Следовательно, в дальней перспективе экспоненциальный рост часто намного превышает полиномиальный.
Кстати, 9 223 372 036 854 775 808–1 — это максимальное значение 64-битного целого числа со знаком.
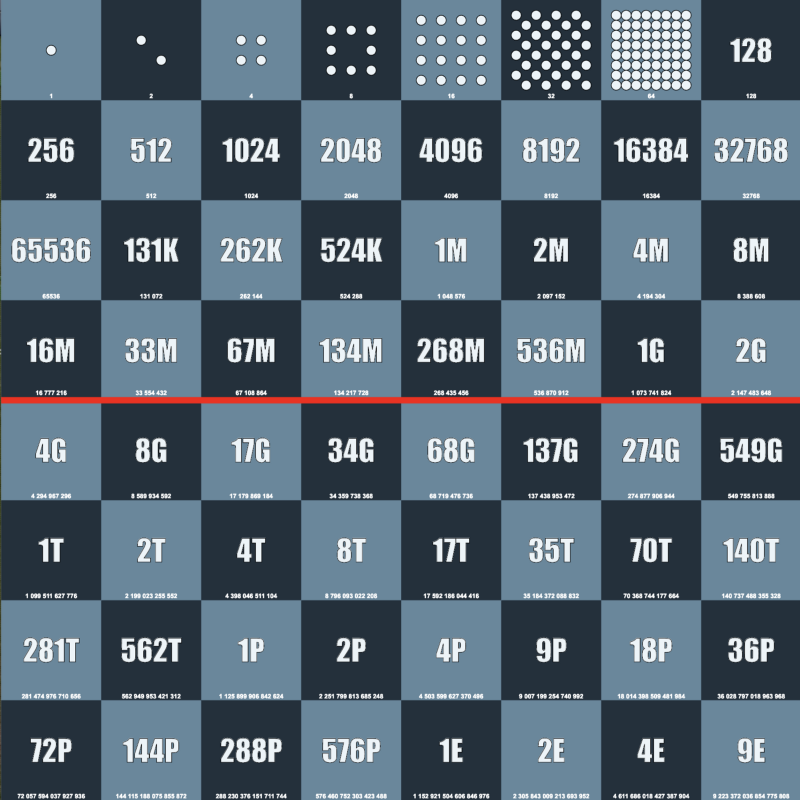
Рисунок 34: источник: Wikipedia
Число e открыл Эйлер. Однако Якоб Бернулли тоже работал с числом e, когда вычислял сложный процент, чтобы заработать больше денег. Если вложить 100 долларов под 10% дохода, то как будет расти эта сумма? Во-первых, это зависит от того, как часто банк рассчитывает проценты. Например, если он рассчитывает один раз, то мы получим в конце года 110 долларов. Если мы передумаем и будем брать проценты каждые 6 месяцев, то в этом случае мы получим больше 110 долларов. Дело в ттом, что процент, полученный за первые 6 месяцев, тоже получит свой процент. Общая сумма будет равна 110,25 долларов. Можно догадаться, что мы можем получить больше денег, если будем забирать деньги каждый квартал года. А если мы будем делать временной интервал всё короче, то окончательные суммы будут продолжать расти. Такой бесконечный сложный процент сделает нас богатыми! Однако наш общий доход стремится к ограниченному значению, связанному с e.
Бернулли не называл число 2,71828 именем e. Когда Эйлер работал с 2,71828, он возвёл экспоненциальную функцию e в степень x. Свои открытия он изложил в книге The Analysis of Infinite.
В 1798 году Томас Мальтус использовал экспоненциальную функцию в своём эссе, посвящённом пищевому дефициту будущего. Он создал линейный график, показывающий производство пищи и экспоненциальный график, показывающий население мира. Мальтус сделал вывод, что в дальней перспективе экспоненциальный рост победит, и мир ждёт серьёзный дефицит пищи. Это явление назвали «мальтузианской катастрофой». Ньютон тоже использовал эту модель, чтобы показать, как охлаждается чашка чая.
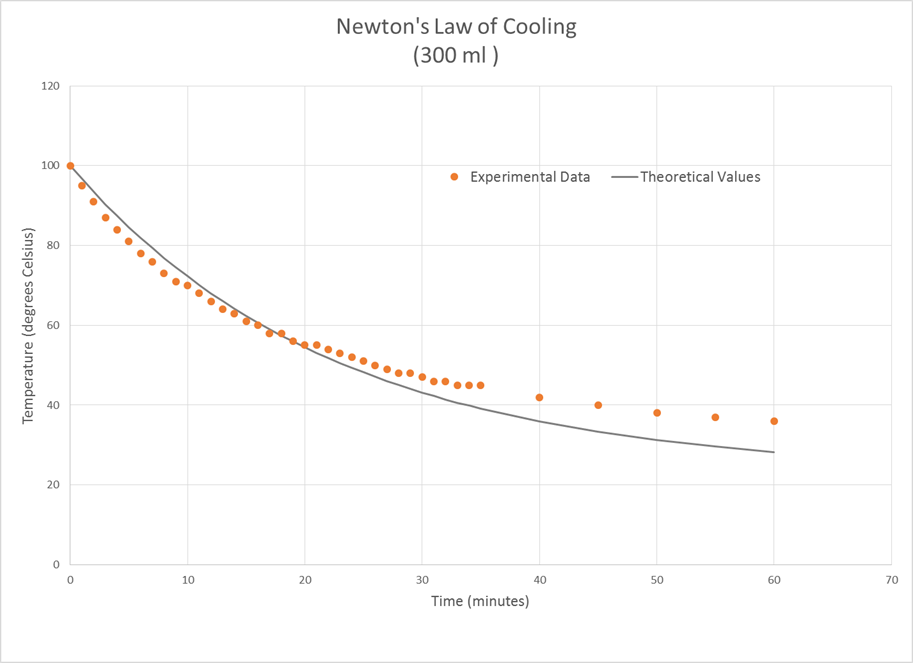
Рисунок 35: закон Ньютона-Рихмана
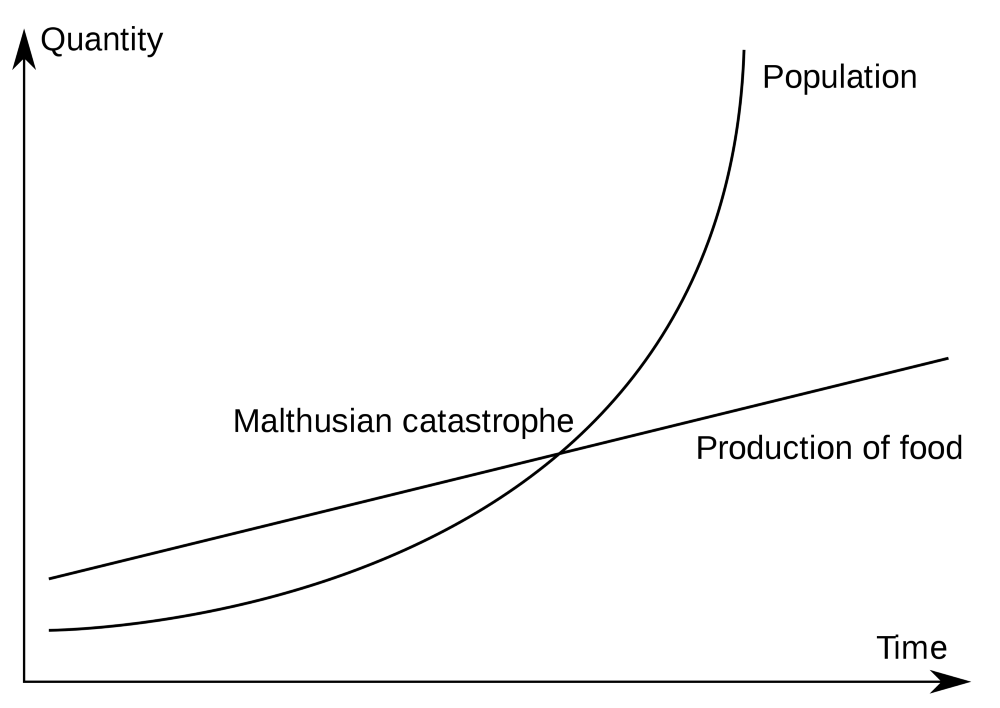
Рисунок 36: мальтузианская катастрофа
Мнимость числа: i, квадратный корень -1
Долгое время для решения своих задач математикам было достаточно обычных чисел. Однако в какой-то момент для дальнейшего развития им потребовалось открыть нечто новое и загадочное. Например, итальянский математик Кардано пытался разделить число 10 на 2 части, произведение которых было бы равно 40. Чтобы решить эту задачу, он записал уравнение: x (10-x) = 40. Когда он решил это квадратное уравнение, то получил два решения: 5 плюс v-15 и 5 минус v-15, что в то время не имело никакого смысла. Этот результат был бессмысленным, потому что по определению квадратного корня ему нужно было найти число, квадрат которого был бы отрицательным. Однако и положительное, и отрицательное числа в квадрате имеют положительное значение. Как бы то ни было, он нашёл своё уникальное число. Однако первым математиком, назвавшим v-1 (квадратный корень из минус единицы) мнимым числом i, был Эйлер.
Лейбниц дал такой комментарий о мнимом числе v-1:
Комплексные числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием.
Мы можем складывать, вычитать, умножать и делить мнимые числа. Сложение, вычитание и умножение просты, а деление немного сложнее. Вещественные и мнимые части складываются по отдельности. В случае умножения i2 будет равно -1.
После Эйлера математик Каспар Вессель представил мнимые числа геометрически с создал комплексную плоскость. Сегодня мы представляем каждое комплексное число a + bi как точку с координатами (a,b).
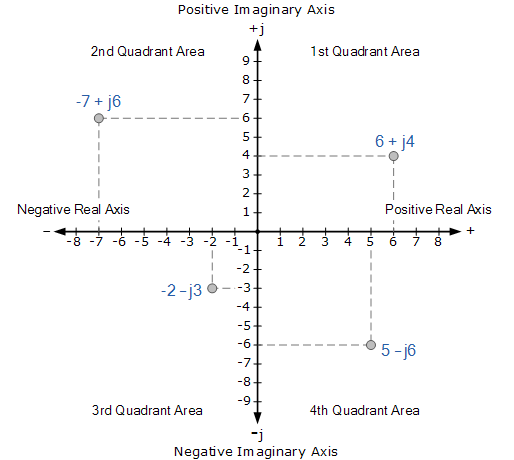
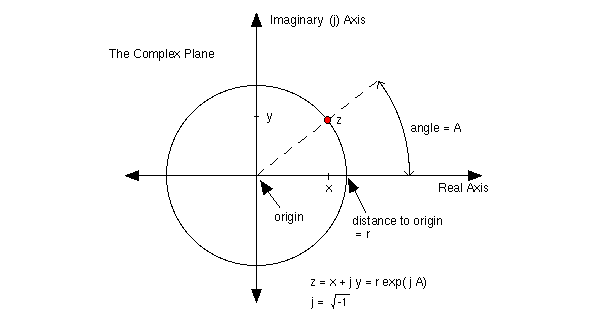
Рисунки 37 и 38: комплексные числа
В викторианскую эпоху многие относились к мнимым числам с подозрением. Однако ирландский математик и астроном Уильям Роуэн Гамильтон покончил с этими сомнениями, определив комплексные числа применительно к кватернионам.
Самое красивое уравнение: тождество Эйлера
Тождество Эйлера связывает экспоненциальную функцию с функциями синуса и косинуса, значения которых колеблются от минус единицы до единицы. Чтобы найти вязь с тригонометрическими функциями, мы можем представить их в виде бесконечного ряда, истинного для всех значений
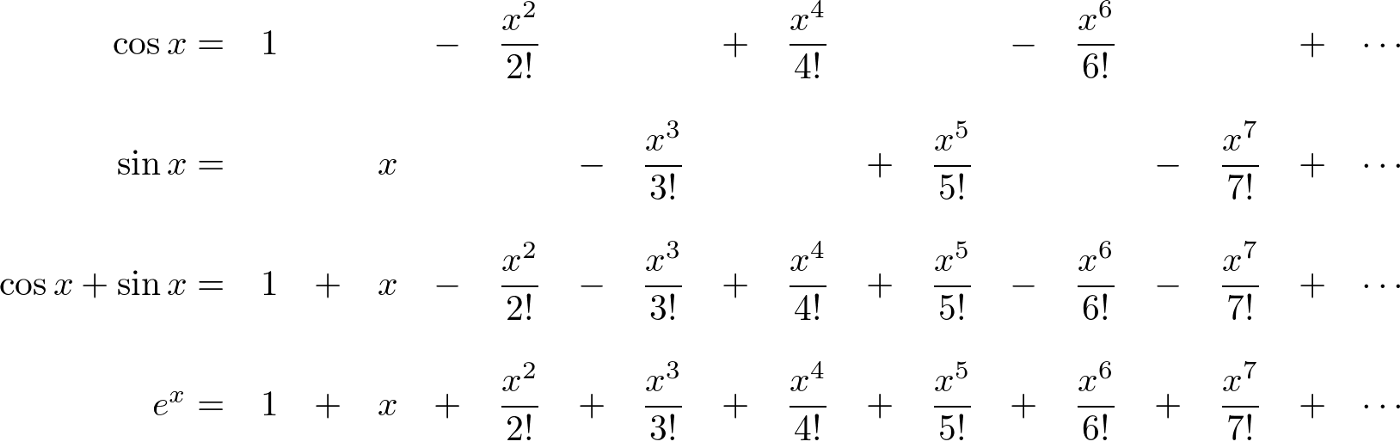
Рисунок 39: открытие тождества Эйлера
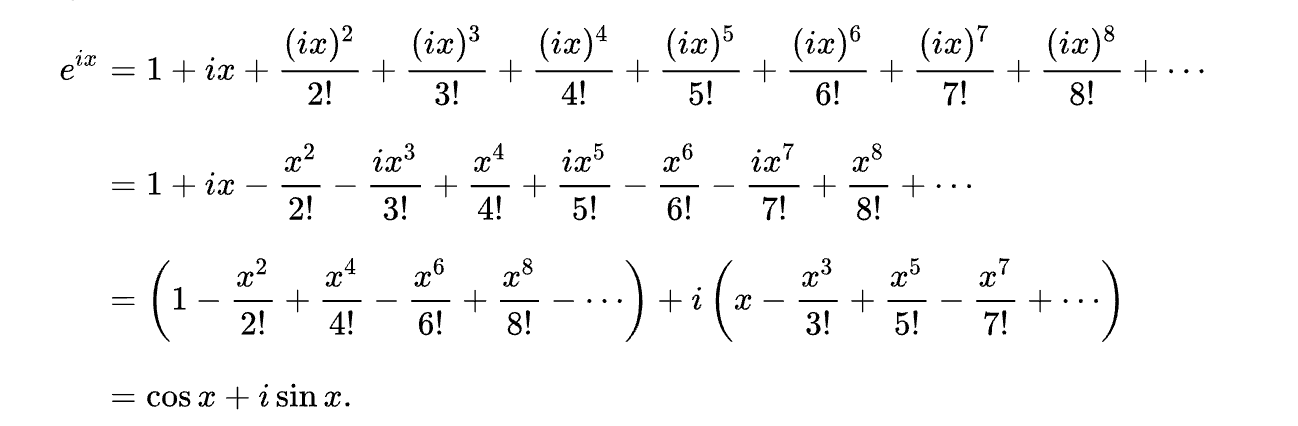
Рисунок 40: тождество Эйлера
Эйлер никогда не записывал это тождество в явном виде, и мы не знаем, кто впервые записал его. Тем не менее, мы связываем его с именем Эйлера в знак почтения перед этим великим первопроходцем математики.
Комментарии (76)
alexxisr
31.05.2019 11:46В 60-ричных вавилонских числах явно видны десятки и единицы. Может они что-то скрывали?
Zenitchik
31.05.2019 12:56Да чё им скрывать? 60-ричная система явно вторична по отношению к 10-чной. Подозреваю, что она создана искусственно над десятичной и двенадцатеричной системами.
OldCoder
01.06.2019 11:3160-ричная это комбинация 5-ричной и 12-ричной систем счисления. Похоже на число пальцев одной руки и число полнолуний в году
vvadzim
01.06.2019 23:5712 это также число фаланг на четырёх пальцах руки. Очень удобно большим пальцем их отсчитывать.
Zenitchik
02.06.2019 13:09Пятиричная, насколько мне известно, в ходу не была. В отличие от десятичной и двенадцатеричной.
maggg
02.06.2019 18:12Это число пальцев и число фаланг: попробуйте пересчитать большим пальцем число фаланг на оставшихся четырёх — вот оно, число двенадцать.
interprise
31.05.2019 12:3136% людей не могу запомнить число пи с точностью 3.14?
Gekus
31.05.2019 12:40Я тоже не верю. Или они должны вообще не знать, что такое пи, или 100% знать 3 цифры 3.14
LoadRunner
31.05.2019 14:15В военное время число Пи могут считать равным 4. Значит 36% — военные.
waxtah
31.05.2019 19:59Тогда окружность будет квадратной.
Gryphon88
31.05.2019 20:55Хм, принудительное перемещение во вселенную с Manhattan distance metric. Не знаете, как посчитать Пи для произвольной метрики?
411
01.06.2019 09:07Кстати в данном случае это будет не Манхэттен, а метрика максимума по всем координатам.
Ссылка с примерами на вики
В случае Манхэттена будет ромб(который в данном случае тоже квадрат, но повёрнутый на 45 градусов). И пи будет 2 корня из 2.
Update:
Хотя если учесть что в Манхэттенской метрике расстояние между двумя вершинами единичного ромба будет 2 я не уверен, что длина стороны ромба в такой метрике останется корнем из 2, а не станет 2. Поэтому возможно там действительно пи=4. Надеюсь кто-то разъяснит.
tvr
01.06.2019 17:42Тогда окружность будет квадратной.
Баян про Василия Ивановича и ПетькуСидят Василий Иванович с Петькой на рельсах, курят. — Василий Иванович, вот ты такой умный, так объясни: рельсы гладкие? — Гладкие! — Колеса круглые? — Круглые! — Почему круглые колеса по гладким рельсам-то стучат? — Дурак ты, Петька! Формулу площади круга знаешь? — Пи эр квадрат? — Вот этим квадратом и стучат!dimonoid
31.05.2019 20:40+1У меня один учитель использует пи=4. Для приблизительных расчетов необходимой скорости вращения сверла. Там 30% ошибка в рамках допуска.
uaggster
31.05.2019 21:57+2А почему не 3?
Или, к примеру, не 3.3, если нужно с избытком?
Почему не 3.2, положим, понятно. А почему не 3.3?
Кстати, концептуально, учитель — прав.
Считать нужно не «как правильно», а как «удобнее, проще и быстрее».
Нужно просто знать, с какой точностью будут эти вычисления.
:-)
Zenitchik
31.05.2019 20:58+3Кстати, гонево. Если посмотреть на используемую военными разных стран угловую меру в тысячных, то Пи в военное время принимает значения от 3 до 3.2 в зависимости от страны.
Окружность делится в разных странах на 6000, 6200 или 6400 «малых делений угломера», причём считается, что тангенс одного малого деления с приемлемой точностью равен 1/1000.
vanxant
31.05.2019 17:53-8Опрос, видимо, среди американских людей. У них во многих штатах в школах пи законодательно приравнено к 3.
catsmile
31.05.2019 22:04+3Как это мило, с помощью устройства, сделанного по американским технологиям, через сеть, сделанную по американским технологиям, писать про то, что «ну тупыыые».
vanxant
31.05.2019 23:18Не угадали:) Устройство, сделанное Малайзии по корейским технологиям и работающее на написанной финским студентом ОС, через сеть на полностью китайских маршрутизаторах, отправил сообщение на сделанный русскими сайт для русских… и далее по списку. И вот только не надо рассказывать, что язык Си и протокол TCP/IP в Штатах изобрели.
Внезапно удивляет количество русскоязычных патриотов США на хабре, раньше такого не было.
DoctorMoriarty
01.06.2019 01:42-3>русскоязычных патриотов США
На самом деле — всего лишь здравомыслящих людей, не видящих смысла в ретранслировании шовинистических шаблонов и баек.
sanalex76
01.06.2019 11:31Написанная финским студентом ОС? Ты серьезно? Между той системой и современным Линуксом дистанция, как между деревянными счетами и компьютером.
Также рекомендую заглянуть на сайт Линукс Фундэшн и посмотреть на основных разработчиков и доноров. Будешь сильно удивлен.vanxant
01.06.2019 16:33-1Да блин, релакс, я просто троллил чувака, у которого кругом исключительно американские технологии. Понятно же, что и ИТ, и наука вообще — это плод коллективных усилий всего мира, а не какой-то одной «исключительной» страны.
catsmile
03.06.2019 11:27Раскладка плюсов и минусов достаточно хорошо показывает, кто какого чувака троллил.
Fen1kz
01.06.2019 01:31+3Эй, полегче, статья же о математике. Давайте не додумывать, а опираться на данные задачи.
37% людей из 941 не смогли назвать больше нуля дробных частей числа пи. Может они спешили, может у них был полон рот, может они сказали 3 — этого мы не знаем. Стоит ли экстраполировать 941 человека на всех людей — это вопрос.
Tyusha
31.05.2019 12:54+1Меня впечатляет немного переиначенное тождество Эйлера: i^i = e^(-pi/2) = 0,2079…
Refridgerator
31.05.2019 13:17Много таких ещё можно придумать, например
Только двойку на что-нибудь более интересное заменить.Refridgerator
31.05.2019 14:30Хотя лучше так:
Менее известное, но более полезное с практической точки зрения (при комплексном x верна только правая часть равенства). При x=1 вырождается в тождество Эйлера, при x=i/2 соответственно в ii.
galaxy
31.05.2019 15:07В такой записи оно уже не будет тождеством. Комплексная степенная/показательная функции многозначны, а это скользкая это дорожка…
Refridgerator
31.05.2019 17:23-3Тригонометрические функции тоже многозначные, но тем не менее тоже имеют место быть тождества.
Gryphon88
31.05.2019 17:35+1Можете пояснить, какая порождающая функция для комплексных чисел? Только взятие корня чётной степени?
MichaelBorisov
31.05.2019 23:47Комплексные числа возникают во многих разделах математики. Они «вылезают» и в интегралах всевозможных, и в диф. уравнениях, и в трансцендентных функциях, преобразование Фурье, да почти где угодно можно их получить. Но корни многочленов — это, наверно, самый простой способ. Кстати, не обязательно степень должна быть чётной. У уравнения x^3=1 имеется 3 корня, 2 из которых комплексные.
Num
01.06.2019 01:02Расширение поля вещественных чисел путём присоединения к нему корня уравнения x^2=-1.
nailer
01.06.2019 19:18+1
Тождество просто завораживающее: связь между пространством мнимых и вещественных чисел…
uvelichitel
31.05.2019 13:20Не вполне раскрыт наглядный/физический смысл числа e, мне кажется. Стоило наверное упомянуть почему логарифм по основанию e называют натуральным, геометрическое дифференцирование натуральной экспоненты и вот это все.
deniskreshikhin
01.06.2019 10:58Да числа e и pi не являются какими-то фундаментальными числами в математике. Они возникают при изучении вещественных чисел и функций от этих чисел. Например, для p-адических чисел нет прямых аналогов. Хотя и те и другие имеют мощность континуума и являются кольцами.
Например число 1 гораздо фундаментальнее, универсальнее и реально более интересно чем e или pi. Но людям хочется сложности, т.к. бесконечные последовательности циферок после запятой будоражат воображение гораздо сильнее чем 1.
Zenitchik
02.06.2019 13:17Числа 0 и 1 — настолько фундаментальны, что их фундаментальность полагается самоочевидной, а потому не упоминается.
deniskreshikhin
02.06.2019 15:31Хах, а вот и не самоочевидно) До начала 20 века даже не существовало строгого определения единицы.
eefadeev
31.05.2019 13:32Действительно трудно не восхищаться таких совершенным уравнением: в нём есть сразу три фундаментальных константы и минимально возможный для описания всего набор чисел. Это очень круто!
Occama
31.05.2019 13:36Начал читать по диагонали, но так до конца и не осилил из-за косяков (которые, в том или ином виде, и в оригинале есть).
Например,1001 = (2^3) + (0^2) + (0^1) + (2^0)
, чисто технически, конечно, верно, но всё же это 1001 = (2^3) + 0*(2^2) + 0*(2^1) + (2^0). В оригинале ближе к этому, но там какая-то дичь с форматированием.
Деление на нуль не допускается, потому что если разделить на ноль, то мы получим число, которое может быть равно любому нужному нам числу, что должно быть запрещено.
Это утверждение имеет под собой почву, если мы ноль делим на ноль. В оригинале более расплывчато, но тоже ощущение, что там какое-то полупонимание.
Прошу прощения, что в комменты, но действительно из-за подобного очень сложно воспринимать.vanxant
31.05.2019 17:55+4Тут и статья не очень, но перевод сделал ее просто ужасной. «Абакус», «Рихман»… буэ
SilenceHabr
01.06.2019 11:31Название рисунка 8.2 «частоты, испускаемые LC-цепью.» тоже несколько удивляет. С тем же успехом можно было назвать«частоты, испускаемые колебанием маятника», при том, что это всего навсего синусоида и косинусоида.
tim2018
31.05.2019 14:48
commanderxo
31.05.2019 15:00Самый большой косяк математики: Эйлер решил взять для определения числа пи диаметр, а не радиус круга. Теперь в огромном количестве формул фигурирует константа 2*pi. А в уравнении Эйлера не было бы внезапной минус единицы.
Рекомендую Tau-Manifesto, весьма познавательно.Refridgerator
31.05.2019 21:21+5Как насчёт тех формул, где присутствует корень из пи — например, гамма-функции от половины целого аргумента или интеграла от гауссианы? А ещё такая формула есть: «Пицца с радиусом ц и толщиной а имеет объём пи·ц·ц·а».
deniskreshikhin
01.06.2019 11:04Радиус круга не так практичен.
Поэтому диаметр практичнее, нужно узнать длину окружности, берёшь штангенциркуль, замеряешь умножаешь на pi.
Ну и наоборот, нужно узнать диаметр бревна, берёшь ленту, измеряешь обхват, делишь на pi, получаешь диаметр.
Радиус в быту не очень нужен.
staticmain
31.05.2019 19:22+3Евклид доказал, что эти соотношения постоянны для всех окружностей, даже для луны, пенни, шины и т.д.
Евклид доказал, что соотношение постоянно для пенни, шины и т.д.? Во времена Евклид были пенни и шины?
maxzhurkin
31.05.2019 22:06+1Деление на нуль не допускается, потому что если разделить на ноль, то мы получим число, которое может быть равно любому нужному нам числу, что должно быть запрещено.
что за бред?
На нуль делить «нельзя» потому, что деление — это решение уравнения, то есть поиск числа, при использовании в качестве сомножителя которого с делителем при умножении получается делимое, а при умножении с нулём в качестве одного из множителей делимое не получается, а получается только нуль
shuhray
31.05.2019 22:34Интересно, что формула встречается у кого-то из современников Ньютона (забыл фамилию) на сто лет раньше Эйлера. С изобретения комплексных чисел прошло лет сто, пока научились ими пользоваться всерьёз.
kvghabr
01.06.2019 00:40+1В голове не укладывается.
Разложим формулу:
e ^ (i*Pi) +1 = 0
2.71 ^ 3.14 = прим. 23.10
23.10 ^ i + 1 = 0 (?)
Или я что-то не понял?Refridgerator
01.06.2019 08:34Так вы продолжайте вычисления:
23.10^i = cos(log(23.10)) + i*sin(log(23.10)) ? -0.999998 + i*0.00176004kvghabr
01.06.2019 20:12+1Вот так более понятно. Видимо, тут неуместно рассуждать в рамках области действительных чисел. И мнимая единица вовсе «не похожа» на таковую действительную.
sergey-b
01.06.2019 01:44+2
gdt
01.06.2019 15:04Простите, но отношение периметра шестиугольника к длине описанной вокруг него окружности никак не может быть равно пи. Для правильного шестиугольника радиус описанной окружности равен длине его стороны. Таким образом, получаем периметр = 6*R, длина описанной окружности = 2*pi*R ? 6.28*R, ваше отношение равно 6/6.28 ? 0.955.
yurixi
01.06.2019 15:27Лично меня уравнение которое говорит что полкруга это пи, потому что пи это полкруга не восхищает. Видимо, привык.
А вот мной открытые самоподобное уравнение:
с пятью элементами из чисел пять —
и
что уравнивает противоположности
таят неразгаданные загадки.
Хотя ладно, конечно разгаданные уже.
Это всего лишь коэффициенты золотого сечения, которые возникает когда полкруга делишь на пять.
Source
01.06.2019 15:36Работая со 96-сторонним многоугольником и применив тот же способ, он получил 2 десятичных разряда пи после запятой: 3 и 10/71 = 3,14084.
Точнее, он определил диапазон:
223/71 < ? < 22/7
Если для него взять среднее, то получится 3.1418511
nailer
01.06.2019 20:25+1Статья «кашеобразная», хотя читал с интересом – название содержанию соответствует лишь в части незначительной: от восхищения гением Эйлера, забыв раскрыть в чём состоит заявленная в названии статьи «самость» тождества, с которого начинал, автор (Ali Kayaspor) решил рассказать о вещах которые его, по-видимому, тоже немало впечатляют. Материал конечно любопытный, и частями может быть использован для просвещения школьников (без сарказма! – сам семиклассникам рассказываю подобное)– если кому-то захочется более строгого изложения введения в системы счисления, практически повторяющего всё изложенное в статье, то рекомендую Квант №6 за 1970 год, статью «Системы счисления» И. М. Яглом. История числа Пи замечательно описана талантливейшим Я. И. Перельманом в «Квадратура круга» (1941). История введения в математический оборот мнимой единицы очень удачно и увлекательно рассказана на Хабре (Откуда есть пошло комплексное число).
Фраза «число Пи нашёл Евклид» – целиком на совести автора исходного текста, я, во всяком случае, полагал более заслуживающим упоминания в данном контексте Архимеда, и с бОльшим акцентом на его заслугах. Считается, что в обращение константу Пи ввёл Уильям Джонс в своей работе 1706 года «Новое введение в математику», само название дано по начальной букве греческих слов «окружность», «периферия», «периметр».
Фраза «Леонард Эйлер открыл число e в 1736 году», тоже, как минимум, некорректна («открыть» Америку можно) – это же число звалось «числом Непера» неспроста (Бернулли был упомянут) – вероятно, было бы правильным сказать, что Эйлер дал этому числу «новую жизнь», также, как он популяризовал и число Пи, и утвердил в математике и «дал жизнь» мнимой единице.
capslocky
02.06.2019 18:04Не все знают, что тождество Эйлера подразумевает, что угол считается в радианах, потому что в градусах было бы уже не так «красиво».
KvanTTT
02.06.2019 18:34Насколько помню, в тригонометрии и в математике в целом по-умолчанию принято считать угол в радианах. Градусы — это уже некоторая искусственность, как и десятичная система счисления (более естественная — двоичная, троичная или хотя бы кратная степени двойки).
uaggster
03.06.2019 09:22Эээ… Градусы — это шестидесятиричная система исчисления. От вавилонян.
Десятичная система исчисления — это грады, от французских реформаторов. Наряду с гильотиной, метром, килограммом.
100 град — прямой угол, 400 град — окружность.
Прижился слабо, к сожалению.Zenitchik
03.06.2019 16:03+1Почему «к сожалению»? 60, в отличие от 100, делится нацело на большинство встречающихся в быту делителей. Наверно, потому вавилоняне его и взяли за основу.
KvanTTT
03.06.2019 16:48Для меня, как математика в большей степени, к сожалению, что прижились градусы. А грады еще хуже.
Кстати, во многих компьютерных играх, особенно старых, в одном обороте 255 градусов (Binary angles). Потому что угол можно хранить всего лишь в одном байте, а также хранить таблицу синусов/косинусов и других тригонометрических функций. Ну и точности в целом достаточно, скорее всего незаметная разница по сравнению с 360 градусами.
Zenitchik
03.06.2019 16:55+1Кстати, во многих компьютерных играх, особенно старых, в одном обороте 255 градусов (Binary angles).
Вероятно 256? Полный оборот по кругу, по идее, должен совпадать с переполнением.
trolley813
Можно еще добавить, что общее количество всех зерен на доске — 18 446 744 073 709 551 615 — максимальное значение 64-битного целого числа без знака (это и логично: в двоичной системе 1111...1 (64 единицы) = 1 + 10 + 100 +… + 1000...0 (63 нуля))