
Как сделать решатель (солвер) нонограмм на Python, переписать его на Rust, чтобы запускать прямо в браузере через WebAssembly.
Начало
Про японские кроссворды (нонограммы) на хабре было уже несколько постов. Пример
и еще один.
Изображения зашифрованы числами, расположенными слева от строк, а также сверху над столбцами. Количество чисел показывает, сколько групп чёрных (либо своего цвета, для цветных кроссвордов) клеток находятся в соответствующих строке или столбце, а сами числа — сколько слитных клеток содержит каждая из этих групп (например, набор из трёх чисел — 4, 1, и 3 означает, что в этом ряду есть три группы: первая — из четырёх, вторая — из одной, третья — из трёх чёрных клеток). В чёрно-белом кроссворде группы должны быть разделены, как минимум, одной пустой клеткой, в цветном это правило касается только одноцветных групп, а разноцветные группы могут быть расположены вплотную (пустые клетки могут быть и по краям рядов). Необходимо определить размещение групп клеток.
Одна из наиболее общепринятых точек зрения — что "правильными" кроссвордами можно называть только те, которые решаются "логическим" путем. Обычно так называют способ решения, при котором не принимаются во внимание зависимости между разными строками и/или столбцами. Иначе говоря, решение представляет собой последовательность независимых решений отдельных строк или столбцов, пока все клетки не окажутся закрашены (подробнее об алгоритме далее). Например только такие нонограммы можно найти на сайте http://nonograms.org/ (http://nonograms.ru/). Нонограммы с этого сайта уже приводились в качестве примера в статье Решение цветных японских кроссвордов со скоростью света. Для целей сравнения и проверки в моем солвере также добавлена поддержка скачивания и парсинга кроссвордов с этого сайта (спасибо KyberPrizrak за разрешение использовать материалы с его сайта).
Однако можно расширить понятие нонограмм до более общей задачи, когда обычный "логический" способ заводит в тупик. В таких случаях для решения приходится делать предположение о цвете какой-нибудь клетки и после, доказав, что этот цвет приводит к противоречию, отмечать для этой клетки противоположный цвет. Последовательность таких шагов может (если хватит терпения) выдать нам все решения. О решении такого более общего случая кроссвордов и будет главным образом эта статья.
Python
Около полутора лет назад я случайно наткнулся на статью, в которой рассказывался метод решения одной строки (как оказалось позднее, метод был довольно медленным).
Когда я реализовал этот метод на Python (мой основной рабочий язык) и добавил последовательное обновление всех строк, то увидел, что решается все это не слишком быстро. После изучения матчасти обнаружилось, что по этой теме существует масса работ и реализаций, которые предлагают разные подходы для этой задачи.
Как мне показалось, наиболее масштабную работу по анализу различных реализаций солверов провел Jan Wolter, опубликовав на своем сайте (который, насколько мне известно, остается самым крупным публичным хранилищем нонограмм в интернете) подробное исследование, содержащее огромное количество информации и ссылок, которые могут помочь в создании своего солвера.
Изучая многочисленные источники (будут в конце статьи), я постепенно улучшал скорость и функциональность моего солвера. В итоге меня затянуло и я занимался реализацией, рефакторингом, отладкой алгоритмов около 10 месяцев в сводобное от работы время.
Основные алгоритмы
Полученный солвер можно представить в виде четырех уровней решения:
(line) линейный солвер: на входе строка из клеток и строка описания (clues), на выходе — частично решенная строка. В python-решении я реализовал 4 различных алгоритма (3 их них адаптированы для цветных кроссвордов). Самым быстрым оказался алгоритм BguSolver, названный в честь первоисточника. Это очень эффективный и фактически стандартный метод решения нонограмм-строки при помощи динамического программирования. Псевдокод этого метода можно найти например в этой статье.
(propagation) все строки и столбцы складываем в очередь, проходим по ней линейным солвером, при получении новой информации при решении строки (столбца) обновляем очередь, соответственно, новыми столбцами (строками). Продолжаем, пока очередь не опустеет.
Пример и кодБерем очередную задачу для решения из очереди. Пусть это будет пустая (нерешенная) строка длины 7 (обозначим ее как
???????) с описанием блоков[2, 3]. Линейный солвер выдаст частично решенную строку?X??XX?, гдеX— закрашенная клетка. При обновлении строки видим, что изменились столбцы с номерами 1, 4, 5 (индексация начинается с 0). Значит в указанных столбцах появилась новая информация и их можно заново отдавать "линейному" солверу. Складываем эти столбцы в очередь задач с повышенным приоритетом (чтобы отдать их линейному солверу следующими).
def propagation(board): line_jobs = PriorityDict() for row_index in range(board.height): new_job = (False, row_index) line_jobs[new_job] = 0 for column_index in range(board.width): new_job = (True, column_index) line_jobs[new_job] = 0 for (is_column, index), priority in line_jobs.sorted_iter(): new_jobs = solve_and_update(board, index, is_column) for new_job in new_jobs: # upgrade priority new_priority = priority - 1 line_jobs[new_job] = new_priority def solve_and_update(board, index, is_column): if is_column: row_desc = board.columns_descriptions[index] row = tuple(board.get_column(index)) else: row_desc = board.rows_descriptions[index] row = tuple(board.get_row(index)) updated = line_solver(row_desc, row) if row != updated: for i, (pre, post) in enumerate(zip(row, updated)): if _is_pixel_updated(pre, post): yield (not is_column, i) if is_column: board.set_column(index, updated) else: board.set_row(index, updated)
(probing) для каждой нерешенной клетки перебираем все варианты цветов и пробуем propagation с этой новой информацией. Если получаем противоречие — выкидываем этот цвет из вариантов цветов для клетки и пытаемся извлечь из этого пользу снова при помощи propagation. Если решается до конца — добавляем решение в список решений, но продолжаем эксперименты с другими цветами (решений может быть несколько). Если приходим к ситуации, где дальше решить невозможно — просто игнорируем и повторяем процедуру с другим цветом/клеткой.
КодВозвращает True, если в результате пробы было получено противоречие.
def probe(self, cell_state): board = self.board pos, assumption = cell_state.position, cell_state.color # already solved if board.is_cell_solved(pos): return False if assumption not in board.cell_colors(pos): LOG.warning("The probe is useless: color '%s' already unset", assumption) return False save = board.make_snapshot() try: board.set_color(cell_state) propagation( board, row_indexes=(cell_state.row_index,), column_indexes=(cell_state.column_index,)) except NonogramError: LOG.debug('Contradiction', exc_info=True) # rollback solved cells board.restore(save) else: if board.is_solved_full: self._add_solution() board.restore(save) return False LOG.info('Found contradiction at (%i, %i)', *pos) try: board.unset_color(cell_state) except ValueError as ex: raise NonogramError(str(ex)) propagation( board, row_indexes=(pos.row_index,), column_indexes=(pos.column_index,)) return True
(backtracking) если при пробинге не игнорировать частично решенный пазл, а продолжать рекурсивно вызывать эту же процедуру — получим бэктрэкинг (иначе говоря — полный обход в глубину дерева потенциальных решений). Здесь начинает играть большую роль, какая из клеток будет выбрана в качестве следующего расширения потенциального решения. Хорошее исследование на эту тему есть в этой публикации.
КодБэктрэкинг у меня довольно неряшливый, но вот эти две функции приблизительно описывают, что происходит при рекурсивном поиске
def search(self, search_directions, path=()): """ Return False if the given path is a dead end (no solutions can be found) """ board = self.board depth = len(path) save = board.make_snapshot() try: while search_directions: state = search_directions.popleft() assumption, pos = state.color, state.position cell_colors = board.cell_colors(pos) if assumption not in cell_colors: LOG.warning("The assumption '%s' is already expired. " "Possible colors for %s are %s", assumption, pos, cell_colors) continue if len(cell_colors) == 1: LOG.warning('Only one color for cell %r left: %s. Solve it unconditionally', pos, assumption) try: self._solve_without_search() except NonogramError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The path %s is invalid", assumption, pos, path) return False if board.is_solved_full: self._add_solution() LOG.warning( "The only color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True continue rate = board.solution_rate guess_save = board.make_snapshot() try: LOG.warning('Trying state: %s (depth=%d, rate=%.4f, previous=%s)', state, depth, rate, path) success = self._try_state(state, path) finally: board.restore(guess_save) if not success: try: LOG.warning( "Unset the color %s for cell '%s'. Solve it unconditionally", assumption, pos) board.unset_color(state) self._solve_without_search() except ValueError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The whole branch (depth=%d) is invalid. ", assumption, pos, depth) return False if board.is_solved_full: self._add_solution() LOG.warning( "The negation of color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True finally: # do not restore the solved cells on a root path - they are really solved! if path: board.restore(save) return True def _try_state(self, state, path): board = self.board full_path = path + (state,) probe_jobs = self._get_all_unsolved_jobs(board) try: # update with more prioritized cells for new_job, priority in self._set_guess(state): probe_jobs[new_job] = priority __, best_candidates = self._solve_jobs(probe_jobs) except NonogramError as ex: LOG.warning('Dead end found (%s): %s', full_path[-1], str(ex)) return False rate = board.solution_rate LOG.info('Reached rate %.4f on %s path', rate, full_path) if rate == 1: return True cells_left = round((1 - rate) * board.width * board.height) LOG.info('Unsolved cells left: %d', cells_left) if best_candidates: return self.search(best_candidates, path=full_path) return True
Итак, мы начинаем решать наш кроссворд со второго уровня (первый годится только для вырожденного случая, когда во всем кроссворде только одна строка или столбец) и постепенно продвигаемся вверх по уровням. Как можно догадаться, каждый уровень несколько раз вызывает нижележащий уровень, поэтому для эффективного решения крайне необходимо иметь быстрые первый и второй уровень, которые для сложных пазлов могут вызываться миллионы раз.
На этом этапе выясняется (довольно ожидаемо), что python — это совсем не тот инструмент, который подходит для максимальной производительности в такой CPU-intensive задаче: все расчеты в нем крайне неэффективны по сравнению с более низкоуровневыми языками. Например, наиболее алгоритмически близкий BGU-солвер (на Java) по результатам замеров оказался в 7-17 (иногда до 27) раз быстрее на самых разных задачах.
pynogram_my BGU_my speedup
Dancer 0.976 0.141 6.921986
Cat 1.064 0.110 9.672727
Skid 1.084 0.101 10.732673
Bucks 1.116 0.118 9.457627
Edge 1.208 0.094 12.851064
Smoke 1.464 0.120 12.200000
Knot 1.332 0.140 9.514286
Swing 1.784 0.138 12.927536
Mum 2.108 0.147 14.340136
DiCap 2.076 0.176 11.795455
Tragic 2.368 0.265 8.935849
Merka 2.084 0.196 10.632653
Petro 2.948 0.219 13.461187
M&M 3.588 0.375 9.568000
Signed 4.068 0.242 16.809917
Light 3.848 0.488 7.885246
Forever 111.000 13.570 8.179808
Center 5.700 0.327 17.431193
Hot 3.150 0.278 11.330935
Karate 2.500 0.219 11.415525
9-Dom 510.000 70.416 7.242672
Flag 149.000 5.628 26.474769
Lion 71.000 2.895 24.525043
Marley 12.108 4.405 2.748695
Thing 321.000 46.166 6.953169
Nature inf 433.138 inf
Sierp inf inf NaN
Gettys inf inf NaN
Замеры проводились на моей машине, пазлы взяты из стандартного набора, который использовал Jan Wolter в своем сравнении
И это уже после того, как я начал использовать PyPy, а на стандартном CPython время расчетов было выше, чем на PyPy в 4-5 раз! Можно сказать, что производительность похожего солвера на Java оказалась выше кода на CPython в 28-85 раз.
Попытки улучшить производительность моего солвера при помощи профайлинга (cProfile, SnakeViz, line_profiler) привели к некоторому ускорению, но сверхъестественного результата конечно не дали.
Итоги:
+ солвер умеет решать все пазлы с сайтов https://webpbn.com, http://nonograms.org и свой собственный (ini-based) формат
+ решает черно-белые и цветные нонограммы с любым количеством цветов (максимальное количество цветов, которое встречалось — 10)
+ решает пазлы с пропущенными размерами блоков (blotted). Пример такого пазла.
+ умеет рендерить пазлы в консоль / в окно curses / в браузер (при установке дополнительной опции pynogram-web). Для всех режимов поддерживается просмотр прогресса решения в реальном времени.
- медленные расчеты (в сравнении с реализациями, описанными в статье-сравнении солверов, см. таблицу).
- неэффективный бэктрэкинг: некоторые пазлы могут решаться часами (когда дерево решений очень большое).
Rust
В начале года я начал изучать Rust. Начал я, как водится, с The Book, узнал про WASM, прошел предлагаемый туториал. Однако хотелось какой-то настоящей задачи, в которой можно зайдействовать сильные стороны языка (в первую очередь его супер-производительность), а не выдуманных кем-то примеров. Так я снова вернулся к нонограммам. Но теперь у меня уже был работающий вариант всех алгоритмов на Python, его осталось "всего лишь" переписать.
С самого начала меня ожидала приятная новость: оказалось что Rust с его системой типов отлично описывает структуры данных для моей задачи. Так например одно из базовых соответствий BinaryColor + BinaryBlock / MultiColor + ColoredBlock позволяет навсегда разделить черно-белые и цветные нонограммы. Если где-то в коде мы попытаемся решить цветную строку при помощи обычных бинарных блоков описания, то получим ошибку компиляции про несоответствие типов.
pub trait Color
{
fn blank() -> Self;
fn is_solved(&self) -> bool;
fn solution_rate(&self) -> f64;
fn is_updated_with(&self, new: &Self) -> Result<bool, String>;
fn variants(&self) -> Vec<Self>;
fn as_color_id(&self) -> Option<ColorId>;
fn from_color_ids(ids: &[ColorId]) -> Self;
}
pub trait Block
{
type Color: Color;
fn from_str_and_color(s: &str, color: Option<ColorId>) -> Self {
let size = s.parse::<usize>().expect("Non-integer block size given");
Self::from_size_and_color(size, color)
}
fn from_size_and_color(size: usize, color: Option<ColorId>) -> Self;
fn size(&self) -> usize;
fn color(&self) -> Self::Color;
}
#[derive(Debug, PartialEq, Eq, Hash, Clone)]
pub struct Description<T: Block>
where
T: Block,
{
pub vec: Vec<T>,
}
// for black-and-white puzzles
#[derive(Debug, PartialEq, Eq, Hash, Copy, Clone, PartialOrd)]
pub enum BinaryColor {
Undefined,
White,
Black,
BlackOrWhite,
}
impl Color for BinaryColor {
// omitted
}
#[derive(Debug, PartialEq, Eq, Hash, Default, Clone)]
pub struct BinaryBlock(pub usize);
impl Block for BinaryBlock {
type Color = BinaryColor;
// omitted
}
// for multicolor puzzles
#[derive(Debug, PartialEq, Eq, Hash, Default, Copy, Clone, PartialOrd, Ord)]
pub struct MultiColor(pub ColorId);
impl Color for MultiColor {
// omitted
}
#[derive(Debug, PartialEq, Eq, Hash, Default, Clone)]
pub struct ColoredBlock {
size: usize,
color: ColorId,
}
impl Block for ColoredBlock {
type Color = MultiColor;
// omitted
}При переносе кода некоторые моменты явно указывали на то, что статически типизированный язык, такой как Rust (ну или, например C++) — более подходящий для этой задачи. Точнее говоря, дженерики и трэйты лучше описывают предметную область чем иерархии классов. Так в Python-коде у меня было два класса для линейного солвера, BguSolver и BguColoredSolver которые решали, соответственно, черно-белую строку и цветную строку. В Rust-коде у меня осталась единственная generic-структура struct DynamicSolver<B: Block, S = <B as Block>::Color>, которая умеет решать оба типа задач, в зависимости от переданного при создании типа (DynamicSolver<BinaryBlock>, DynamicSolver<ColoredBlock>). Это, конечно, не значит, что в Python что-то похожее невозможно сделать, просто в Rust система типов явно указала мне, что если не пойти эти путем, то придется написать тонну повторяющегося кода.
К тому же любой кто пробовал писать на Rust, несомненно заметил эффект "доверия" к компилятору, когда процесс написания кода сводится к следующему псевдометаалгоритму:
write_initial_code
while (compiler_hints = $(cargo check)) != 0; do
fix_errors(compiler_hints)
end
Когда компилятор перестанет выдавать ошибки и предупреждения, ваш код будет согласован с системой типов и borrow checker-ом и вы заранее предупредите возникновение кучи потенциальных багов (конечно, при условии тщательного проектирования типов данных).
Приведу пару примеров функций, которые показывают насколько лаконичен может быть код на Rust (в сравнении с Python-аналогами).
Выдает список нерешенных "соседей" для данной точки (x, y)
def unsolved_neighbours(self, position):
for pos in self.neighbours(position):
if not self.is_cell_solved(*pos):
yield posfn unsolved_neighbours(&self, point: &Point) -> impl Iterator<Item = Point> + '_ {
self.neighbours(&point)
.into_iter()
.filter(move |n| !self.cell(n).is_solved())
}Для набора блоков, описывающих одну строку, выдать частичные суммы (с учетом обязательных промежутков между блоками).Полученные индексы будут указывать минимальную позицию, на которой блок может закончиться (эта информация используется далее для линейного солвера).
Например для такого набора блоков [2, 3, 1] имеем на выходе [2, 6, 8], что означает, что первый блок может быть максимально сдвинут влево настолько, чтобы его правый край занимал 2-ую клетку, аналогично и для остальных блоков:
1 2 3 4 5 6 7 8 9
_ _ _ _ _ _ _ _ _
2 3 1 |_|_|_|_|_|_|_|_|_|
^ ^ ^
| | |
конец 1 блока | | |
конец 2 блока -------- |
конец 3 блока ------------
@expand_generator
def partial_sums(blocks):
if not blocks:
return
sum_so_far = blocks[0]
yield sum_so_far
for block in blocks[1:]:
sum_so_far += block + 1
yield sum_so_farfn partial_sums(desc: &[Self]) -> Vec<usize> {
desc.iter()
.scan(None, |prev, block| {
let current = if let Some(ref prev_size) = prev {
prev_size + block.0 + 1
} else {
block.0
};
*prev = Some(current);
*prev
})
.collect()
}При портировании я допустил несколько изменений
- ядро солвера (алгоритмы) подверглись незначительным изменениям (в первую очередь для поддержки generic-типов для клеток и блоков)
- оставил единственный (самый быстрый) алгоритм для линейного солвера
- вместо ini формата ввел чуть измененный TOML-формат
- не добавил поддержку blotted-кроссвордов, потому что, строго говоря, это уже другой класс задач
оставил единственный способ вывода — просто в консоль, но теперь цветные клетки в консоли рисуются действительно цветными (благодаря этому крэйту)
вот так
Полезные инструменты
- clippy — стандартный статический анализатор, который иногда даже может дать советы, слегка увеличивающие производительность кода
- valgrind — инструмент для динамического анализа приложений. Я использовал его как профайлер для поиска боттлнеков (
valrgind --tool=callgrind) и особо прожорливых по памяти участков кода (valrgind --tool=massif). Совет: устанавливайте [profile.release] debug=true в Cargo.toml перед запуском профайлера. Это позволит оставить debug-символы в исполняемом файле. - kcachegrind для просмотра файлов callgrind. Очень полезный инструмент для поиска наиболее проблемных с точки зрения производительности мест.
Производительность
То, ради чего и затевалось переписывание на Rust. Берем кросвворды из уже упомянутой таблицы сравнения и прогоняем их через лучшие, описанные в оригинальной статье, солверы. Результаты и описание прогонов здесь. Берем полученный файл и строим на нем пару графиков.Так как время решения варьируется от миллисекунд до десятков минут, график выполнен с логарифмической шкалой.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# strip the spaces
df = pd.read_csv('perf.csv', skipinitialspace=True)
df.columns = df.columns.str.strip()
df['name'] = df['name'].str.strip()
# convert to numeric
df = df.replace('\+\ *', np.inf, regex=True)
ALL_SOLVERS = list(df.columns[3:])
df.loc[:,ALL_SOLVERS] = df.loc[:,ALL_SOLVERS].apply(pd.to_numeric)
# it cannot be a total zero
df = df.replace(0, 0.001)
#df.set_index('name', inplace=True)
SURVEY_SOLVERS = [s for s in ALL_SOLVERS if not s.endswith('_my')]
MY_MACHINE_SOLVERS = [s for s in ALL_SOLVERS if s.endswith('_my') and s[:-3] in SURVEY_SOLVERS]
MY_SOLVERS = [s for s in ALL_SOLVERS if s.endswith('_my') and s[:-3] not in SURVEY_SOLVERS]
bar_width = 0.17
df_compare = df.replace(np.inf, 10000, regex=True)
plt.rcParams.update({'font.size': 20})
def compare(first, others):
bars = [first] + list(others)
index = np.arange(len(df))
fig, ax = plt.subplots(figsize=(30,10))
df_compare.sort_values(first, inplace=True)
for i, column in enumerate(bars):
ax.bar(index + bar_width*i, df_compare[column], bar_width, label=column[:-3])
ax.set_xlabel("puzzles")
ax.set_ylabel("Time, s (log)")
ax.set_title("Compare '{}' with others (lower is better)".format(first[:-3]))
ax.set_xticks(index + bar_width / 2)
ax.set_xticklabels("#" + df_compare['ID'].astype(str) + ": " + df_compare['name'].astype(str))
ax.legend()
plt.yscale('log')
plt.xticks(rotation=90)
plt.show()
fig.savefig(first[:-3] + '.png', bbox_inches='tight')
for my in MY_SOLVERS:
compare(my, MY_MACHINE_SOLVERS)
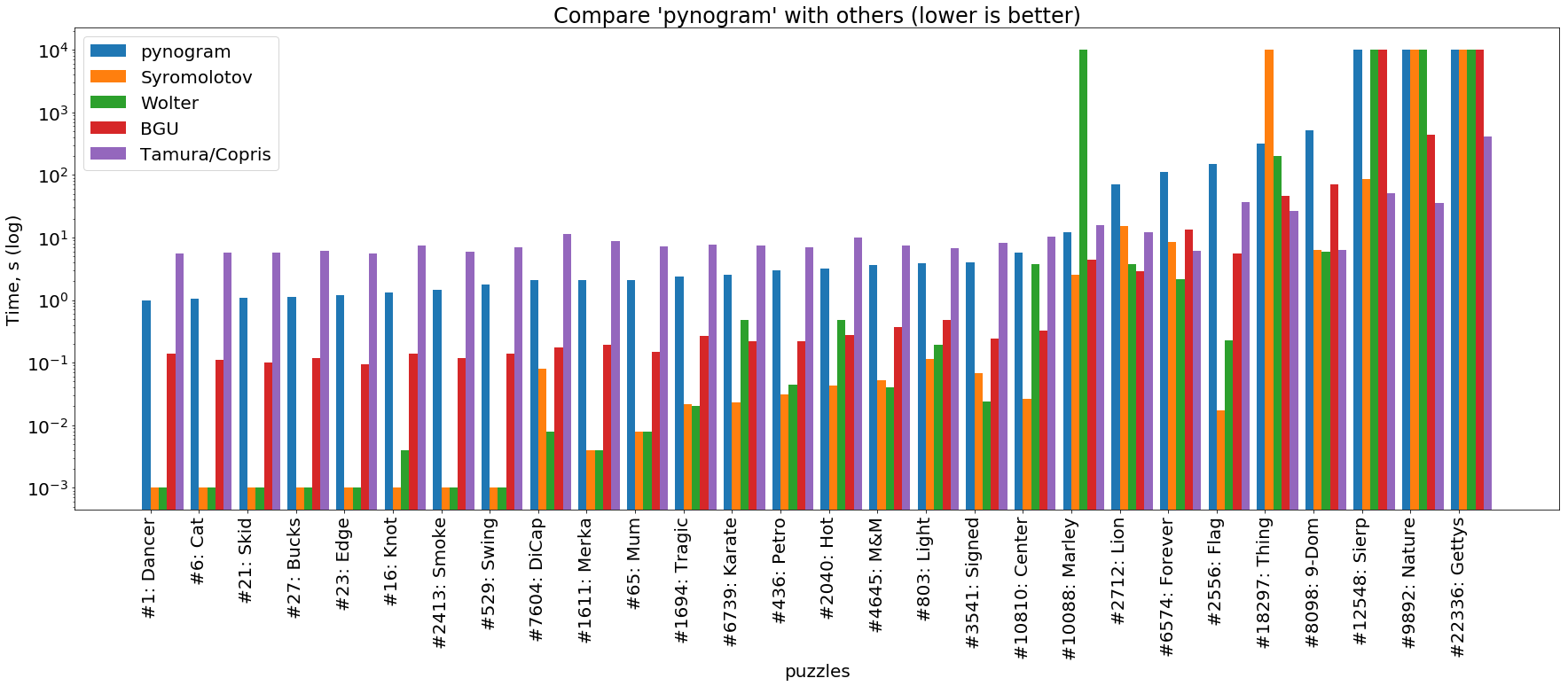
compare(MY_SOLVERS[0], MY_SOLVERS[1:])python-солвер
Видим, что pynogram здесь медленнее всех представленных солверов. Единственное исключение из этого правила — солвер Tamura/Copris, основанный на SAT, который самые простые пазлы (левая часть графика) решает дольше, чем наш. Однако такова уж особенность SAT-солверов: они предназначены для супер сложных кроссвордов, в которых обычный солвер надолго застревает в бэктрэкинге. Это отчетливо видно на правой части графика, где Tamura/Copris решает самые сложные пазлы в десятки и сотни раз быстрее всех остальных.
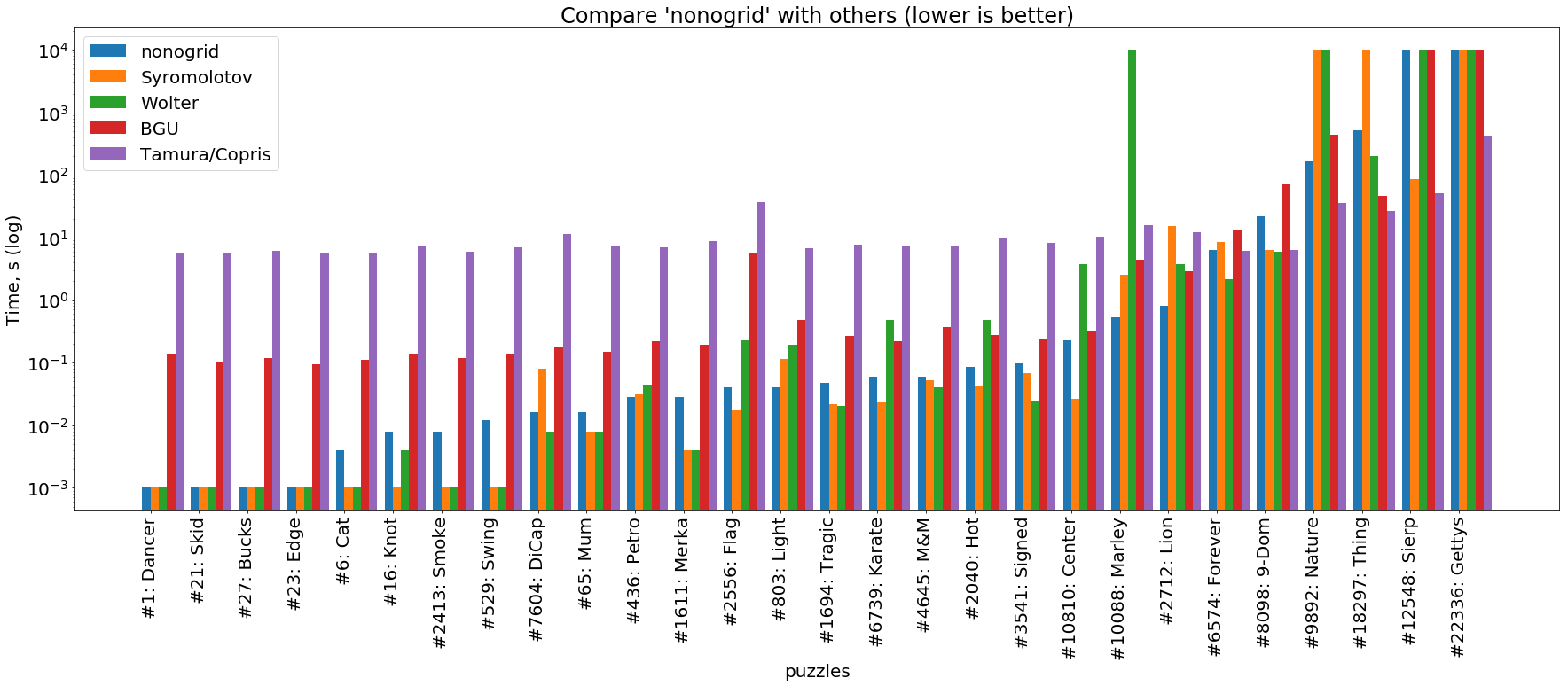
rust-солвер
На этом графике видно, что nonogrid на простых задачах справляется также или чуть хуже, чем высокопроизводительные солверы, написанные на C и С++ (Wolter и Syromolotov). С усложнением задач, наш солвер примерно повторяет траекторию BGU-солвера (Java), но почти всегда опережает его примерно на порядок. На самых сложных задачах Tamura/Copris как всегда впереди всех.
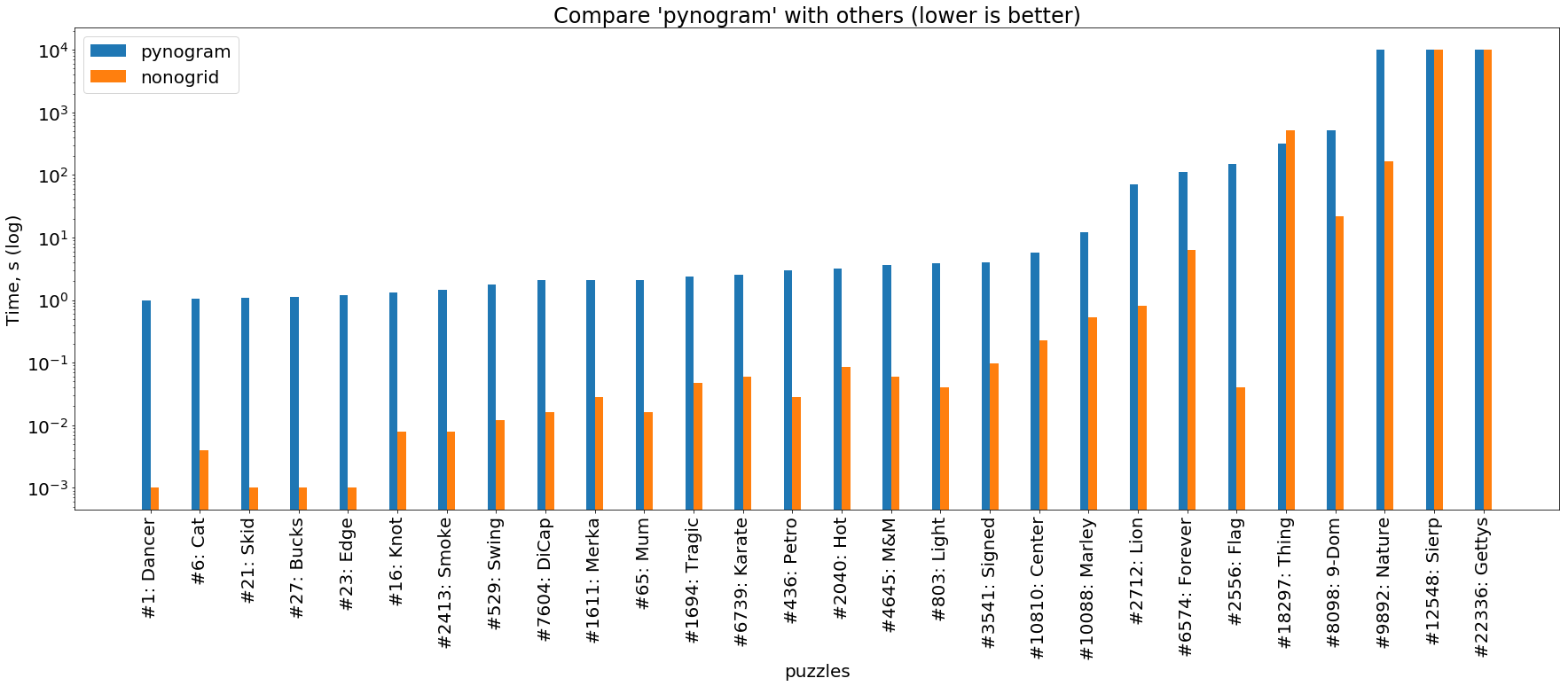
rust vs python
Ну и наконец сравнение двух наших солверов, описанных здесь. Видно, что Rust-солвер почти всегда опережает на 1-3 порядка питоновский солвер.
Итоги:
+ солвер умеет решать все пазлы с сайтов https://webpbn.com (кроме blotted — c частично скрытыми размерами блоков), http://nonograms.org и свой собственный (TOML-based) формат
+ решает черно-белые и цветные нонограммы с любым количеством цветов
+ умеет рендерить пазлы в консоль (цветные c webpbn.com рисует по настоящему цветными)
+ работает быстро (в сравнении с реализациями, описанными в статье-сравнении солверов, см. таблицу).
- бэктрэкинг остался неэффективным, как и в Python-решении: некоторые пазлы (например вот такой безобидный 20x20) могут решаться часами (когда дерево решений очень большое). Возможно вместо бэктрэкинга стоит воспользоваться уже упоминавшимися на хабре SAT-солверами. Правда единственный найденный мною SAT-солвер на Rust на первый взгляд кажется недописанным и заброшенным.
WebAssembly
Итак, переписывание кода на Rust дало свои плоды: солвер стал намного быстрее. Однако Rust нам предлагает еще одну невероятно крутую фичу: компиляцию в WebAssembly и возможность запускать свой код прямо в браузере.
Для реализации этой возможности существует специальный инструмент для Rust, который обеспечивает необходимые биндинги и генерирует за вас boilerplate для безболезненного запуска Rust функций в JS-коде — это wasm-pack (+wasm-bindgen). Большая часть работы c ним и другими важными инструментами уже описана в туториале Rust and WebAssembly. Однако есть пара моментов, которые пришлось выяснять самостоятельно:
при чтении создается ощущение, что туториал в первую очередь написан для JS-девелопера, который хочет ускорить свой код при помощи Rust. Ну или по крайней мере, для того кто знаком с npm. Для меня же, как человека, далекого от фронтэнда, было удивлением обнаружить, что даже стандартный пример из книги никак не хочет работать со сторонним web-сервером, отличающимся от
npm run start.
К счастью в wasm-pack есть режим, позволяющий генерировать обычный JS-код (не являющийся npm-модулем).
wasm-pack build --target no-modules --no-typescriptна выходе даст всего два файла: project-name.wasm — бинарник Rust-кода, скомпилированного в WebAssembly и project-name.js. Последний файл можно добавить на любую HTML-страницу<script src="project-name.js"></script>и использовать WASM-функции, не заморачиваясь с npm, webpack, ES6, модулями и прочими радостями современного JS-разработчика. Режимno-modulesидеально подходит для не-фронтэндеров в процессе разработки WASM-приложения, а также для примеров и демонстраций, потому что не требует никакой дополнительной frontend-инфраструктуры.
WemAssembly хорош для задач, которые слишком тяжелы для JavaScript. В первую очередь это задачи, которые выполняют множество расчетов. А раз так, такая задача может выполняться долго даже с WebAssembly и тем самым нарушить асинхронный принцип работы современного веба. Я говорю про всевозможные Warning: Unresponsive script, которые мне случилось наблюдать при работе моего солвера. Для решения этой проблемы можно использовать механизм Web worker. В таком случае схема работы с "тяжелыми" WASM-функциями может выглядеть так:
- из основного скрипта по событию (например клику на кнопке) послать сообщение воркеру с заданием запустить тяжелую функцию.
- воркер принимает задание, запускает функцию и по ее окончанию возвращает результат.
- основной скрипт принимает результат и как-то его обрабатывает (отрисовывает)
При создании WASM-интерфейса нет возможности передавать все создаваемые типы данных в JS, к тому же это противоречит практике использования WASM. Однако между вызовами функций нужно как-то хранить состояние (внутреннее представление нонограмм с описанием клеток и блоков), поэтому я использовал глобальный HashMap для хранения нонограмм по их порядковым номерам, который никак не виден снаружи. При запросе извне (из JS) передается только номер кроссворда, по которому затем восстанавливается сам кроссворд для запуска решения / запроса результатов решения.
Для обеспечения безопасного доступа к глобальному словарю, он заворачивается в Mutex, что заставляет заменить все используемые структуры на thread-safe. Изменения в таком случае касаются использования smart-указателей в основном коде солвера. Для поддержки thread-safe операций пришлось заменить все Rc на Arc и RefCell на RwLock. Однако эта операция тут же сказалась на производительности солвера: время выполнения по самой оптимистичной оценке увеличилось на 30%. Для обхода этого ограничения я добавил специальную опцию --features=threaded при необходимости использовать солвер в thread-safe среде, которая и необходима в WASM-интерфейсе.
В результате проведенных замеров на кроссвордах 6574 и 8098 получился следующий результат (лучшее время в секундах из 10 запусков):
| id | non-thread-safe | thread-safe | web-interface |
|---|---|---|---|
| 6574 | 5.4 | 7.4 | 9.2 |
| 8098 | 21.5 | 28.4 | 29.9 |
Видно, что в веб-интерфейсе пазл решается на 40..70% медленнее, чем при запуске нативного приложения в консоли, причем большую часть этого замедления (32..37%) берет на себя запуск в thread-safe режиме (cargo build --release --features=threaded).
Тесты проводились в Firefox 67.0 и Chromium 74.0.
WASM-солвер можно попробовать здесь (исходники). Интерфейс позволяет выбрать кроссворд по его номеру с одного из сайтов https://webpbn.com/ или http://www.nonograms.org/
TODO
"выкидывание" решенных строк/столбцов, чтобы облегчить/ускорить решение на этапе бэктрэкинга.
если солвер находит несколько решений, то интерфейс их не показывает. Вместо этого он показывает максимально "общее" решение, то есть неполное решение, в котором незакрашенные клетки могут иметь разные значения. Нужно добавить показ всех найденных решений.
нет ограничения по времени (некоторые пазлы считаются очень долго, традиционно я запускал с таймаутом 3600 секунд). В WASM невозможно использовать системный вызов времени, чтобы запустить ограничивающий таймер (на самом деле, это единственное (!) изменение, которое пришлось сделать, чтобы солвер заработал в WASM). Это, я уверен, как-то можно пофиксить, но возможно придется в основной крэйт nonogrid вносить изменения.
невозможно отслеживать прогресс. Здесь у меня есть некоторые наработки: коллбэки, которые могут срабатывать при изменении состояния клеток, но как их пробросить в WASM пока не думал. Возможно стоит создать очередь, привязанную к пазлу и писать в нее все (или основные) изменения на этапе решения, а со стороны JS сделать цикл, вычитывающий эту очередь и рендерящий изменения.
уведомления об ошибках в JS. Например при запросе несуществующего пазла в консоль вываливается backtrace, но на странице просто ничего не происходит.
добавить поддержку других источников и внешних нонограмм (например возможность загружать файлы в TOML-формате)
Итоги
задача решения нонограмм позволила мне получить массу новых знаний об алгоритмах, языках и инфраструктуре (профайлерах, анализаторах, etc).
солвер на Rust на 1-3 порядка быстрее солвера на PyPy при увеличении количества кода всего в 1.5-2 раза (точно не замерял).
переносить код с Python на Rust достаточно просто, если он разбит на достаточно мелкие функции и использует функциональные возможности Python (итераторы, генераторы, comprehensions), которые замечательно транслируются в идиоматичный Rust-код.
писать на Rust под WebAssembly можно уже сейчас. При этом производительность исполнения Rust кода, скомпилированного в WASM, довольно близка к нативному приложению (на моей задаче примерно в 1.5 раза медленнее).
Основные источники
- The 'pbnsolve' Paint-by-Number Puzzle Solver by Jan Wolter and the survey
- The BGU Nonograms Project
- Solving Nonograms by combining relaxations
- An Efficient Approach to Solving Nonograms
- Решение цветных японских кроссвордов со скоростью света
- Color and black and white Japanese crosswords on-line
- Решение японских кроссвордов с использованием конечных автоматов
- 'Nonolib' library by Dr. Steven Simpson
- Rust and WebAssembly
Комментарии (34)

andy_p
03.06.2019 14:25Не понял, за какое время ваша программа решила тест 22336? У вас там шкала закончилась.

T_12 Автор
03.06.2019 15:08За час не решилась, остановлено по таймауту — это то, что обозначено '+' в оригинальной таблице-сравнении. Для графиков я просто подставил значение 10000 секунд, чтобы не с бесконечностью оперировать.

andy_p
03.06.2019 15:18Значит, не все тесты решаются.

T_12 Автор
03.06.2019 15:28Да, из всего сайта webpbn.com 6 черно-белых не решаются до конца и еще больше цветных.

andy_p
03.06.2019 15:41Тогда утверждение "солвер умеет решать все пазлы с сайтов https://webpbn.com" не соответствует действительности.

T_12 Автор
03.06.2019 15:50«решать» != «находить решения». Речь здесь о принципиальной возможности, а не о конечном результате. Например большинство солверов не умеют решать цветные кроссворды. Хотя формально вы правы — я не добавил поддержку blotted-кроссвордов, хотя в Python-солвере она была.

andy_p
03.06.2019 16:35Хм… При всем уважении, решать — это именно находить решения. Что толку от солвера, если он потратит год на решение и ничего не найдет ?

T_12 Автор
03.06.2019 17:11У меня написано «умеет решать», а вы трактуете как «может решить». Вы ведь не станете говорить, что шахматист, который проигрывает партию другому «не умеет играть», он скорее «не смог победить». А вот те солверы, которые не умеют решать цветные — они как шахматисты, которые в принципе не умеют играть в го. Иначе говоря, несмотря на то что, глаголы «решать» и «решить» похожи — это все таки разные глаголы. Первый — о процессе, второй — о результате.

T_12 Автор
05.06.2019 10:59Запустил #22336 на машине послабее — через 26 часов нашлось два решения (94020 сек). Все же получилось значительно меньше года. Конечно ваш солвер решает ту же задачу меньше чем за 2 минуты и это очень круто.

akk0rd87
03.06.2019 15:18Не пробовали написать алгоритм составления/решения филиппинских кроссвордов?

hfinn
04.06.2019 05:21+1Реквестирую прогон на www.spoj.com/problems/JCROSS
Там как раз на Rust никто не решал ещё.
T_12 Автор
04.06.2019 20:17Это дело конечно хорошее, только там Rust 1.14.0 используется, где куча сахара еще не введена и, например, у итераторов значительно меньше методов. Но для спортивного интереса думаю можно попробовать переделать под Rust образца 2016.

hfinn
05.06.2019 07:26Видимо, поэтому и неохота никому связываться. Хотя в списке пожеланий «Rust — update compiler to more pragmatic version» там с прошлого года висит — может и не стоит переделывать пока — вдруг обновят в ближайшее время.

T_12 Автор
06.06.2019 12:59Попробовал загнать туда минимальный пример — получил таймаут. Возможно там билдится без оптимизаций, поэтому получается медленный debug-код.

zhekas
06.06.2019 14:04Там есть проблемный кроссворд. Попробуй не делать backtracking у 198-ого по порядку кроссворда. У меня с ним были проблемы.

T_12 Автор
06.06.2019 20:32поменял стратегию выбора кандидата для бэктрэкинга и все тесты удалось решить

hfinn
07.06.2019 04:22Ну вот, работает машинка-то. Нам бы только иностранное ругать © :)
Быстро у вас получилось. За 12 подходов всего.
T_12 Автор
07.06.2019 10:19Половину этих подходов я пытался выяснить, почему выдает 'Wrong Answer' и при этом не дает никаких подсказок, что же пошло не так. Оказалось, что никакие другие символы, кроме '.' и '#' нельзя писать, иначе задача сразу считается проваленной. А у меня для неопределенных (нерешенных) клеток раньше выводил символ '?'.
Вторая половина запусков — это да, здесь я пытался поменять стратегию бэктрэкинга так, чтобы без таймаута все решить.

LoadRunner
04.06.2019 12:13Признаюсь, я читал на скроллинге, но описание используемых шагов для решения прочёл внимательно. Я правильно понял, что для решения цветных кроссвордов используется такой же набор алгоритмов, что и для чёрно-белых? То есть, для одноцветных (отсутствие цвета и точки не цвет).
Ведь решение цветных кроссвордов сводится к решению одноцветных — берётся каждый цвет отдельно и решается как одноцветный. Зашли в тупик — переключились на другой цвет, но с учётом решения по предыдущему цвету.
Или именно такой алгоритм для многоцветных кроссвордов и был реализован, а я просто не увидел?
T_12 Автор
04.06.2019 13:33Все этапы решения — параметрические по типу блока (BinaryBlock или ColoredBlock). То есть все функции имеют примерно такую сигнатуру
fn solve<B: Block>(...);. Алгоритмы ничего не знают, о том что они решают, потенциально можно добавить еще какую-нибудь пару типовimpl Block for SomeOtherBlock; impl Color for SomeOtherColorпомимо имеющихся сейчасBinaryColor + BinaryBlock; MultiColor + ColoredBlock, которые будут задавать еще какую-то схему взаимодействия между отдельными числовыми блоками и клетками нонограмм и все алгоритмы должны без проблем эту схему подхватить. Короче говоря, черно-белые — это не частный случай цветных, а совершенно отдельная схема.

zhekas
05.06.2019 20:42+1О, мой solver в статистике (Syromolotov). С тех пор добавил несколько идей по backtracking-у
Здесь начинает играть большую роль, какая из клеток будет выбрана в качестве следующего расширения потенциального решения.
И вот тут начинается самое интересное. Распишу по этапам эволюции моего backtracking
1) Очевидно (может и не очевидно, но эксперементально проверено), что выбор клеток по порядку не лучший вариант.
2) Логично предположить, что если выбрать клетку, которая на этапе «probing» даёт больше закрашиваемых клеток, то это даст лучший результат. Тут у меня появилось два метода (я писал только черно-белый решатель):
а) Искать клетку у которой один цвет даёт максимальный результат и начинать с него.
б) Искать клетку, у которой минимум по двум цветам (черный и белый) даёт максимальный результат и начинать с максимального цвета.
Метод б) эксперементально даёт лучший результат. Но голый этап 2 тоже не продуктивный, так как на каждом этапе поиска клетки (уровне рекурсии backtracking-а) приходится делать probing по всем незакрашенным клеткам.
3) А что если на каждом уровне рекурсии backtracking-а делать probing не по всем незакрашенным клеткам, а только по тем, у которой набор закрашиваемых клеток пересекается с набором закрашиваемых клеток с выбранной клеткой на предыдущем этапе. Для этого после каждого probinga клетки его закрашиваемые клетки записываются в список закрашиваемых. И наоборот в закрашенную после probingа клетку помещается список тех клеток, которые её закрасили. Данный этап дал огромный скачек в решений, который задвинул меня в список лидирующих солверов в webpbn.com/survey
4) Последний этап на данный момент (который уже писался после попадания в webpbn.com/survey). Проблемы есть из-за последовательного выполнения рекурсии. Покажем на примере. Допустим у нас есть 3 уровня рекурсии
1 уровень. Мы нашли клетку1 и пошли в черный цвет
2 уровень. Мы нашли клетку2 и пошли в чёрный цвет
3 уровень. Мы нашли клетку3 и пошли в черный цвет. Узнали, что черный цвет ошибочен проверили белый цвет. Узнали что он тоже ошибочен. И пошли на уровень ниже. То есть на уровень2. И там меняем клетку2 на белую и возвращаемся в уровень3.
А что если закрашенные клетки на уровне 3 и закрашенные клетки на уровне 2 не зависимы друг от друга (например находятся вообще в разных углах кроссворда и никак друг на друга не влияют). Тогда получается, что мы зря вернулись на уровень2. А сразу могли бы вернутся на уровень 1 и проверять белый цвет Клетки1. Если между зависимыми уровнями, например 10 независимых, то это огромная работа сделанная впустую.
Для того, чтобы выявить зависимость между уровнями, я при закрашивании клеток в probing-е, помечаю какие клетки повлияли на выбор этого цвета и смотрю, в каком уровне они были закрашены. После этого можно смело пропускать уровни, которые не повлияли на закрашивания уровня n.
4-й этап дал так же очень хороший скачок в решении.
T_12 Автор
05.06.2019 21:05Круто, что нашелся автор одного из самых быстрых солверов!
По пунктам 1 и 2: я для стратегии выбора лучшего кандидата изучал это исследование и на моем солвере лучший результат показала стратегия Sqrt (см. раздел V. EXPERIMENTS).
Пункт 3 — это что-то новенькое, надо будет у себя попробовать сделать.
Пункт 4 очень похож на стратегию «срезания» ветвей дерева поиска, называемую «backjumping». У меня были планы по ее реализации, но руки пока не дошли.
Спасибо за подробное описание идей.
zhekas
05.06.2019 21:50Круто, что нашелся автор одного из самых быстрых солверов!
К сожалению, Данная статистика теряет актуальность.Страница webpbn.com/survey не обновлялась с
Last Update: Wed Sep 25 06:35:01 PDT 2013
А товарищ Jan Wolter (jan) (создатель этого сайта, собиратель этой статистики, автор pbnsolver) — умер в декабре 13-го — январе 14-го


helgihabr
T_Sun
Обратите внимание на шкалу ординат, она логарифмическая
helgihabr
Теперь увидел, спасибо.