Хабр, привет.

Этот пост — краткий обзор общих алгоритмов машинного обучения. К каждому прилагается краткое описание, гайды и полезные ссылки.

Метод главных компонент (PCA)/SVD

Это один из основных алгоритмов машинного обучения. Позволяет уменьшить размерность данных, потеряв наименьшее количество информации. Применяется во многих областях, таких как распознавание объектов, компьютерное зрение, сжатие данных и т. п. Вычисление главных компонент сводится к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных или к сингулярному разложению матрицы данных.



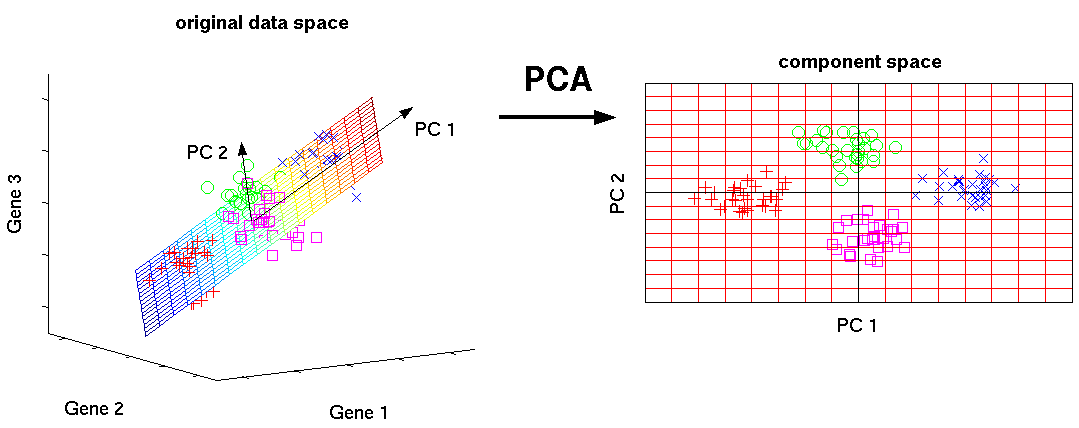
SVD — это способ вычисления упорядоченных компонентов.

Полезные ссылки:

• scipy.linalg.svd
• sklearn.decomposition.pca

Вводный гайд:

• Учебное пособие по основному анализу компонентов

Метод наименьших квадратов

Метод наименьших квадратов — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, а также для аппроксимации точечных значений некоторой функции.



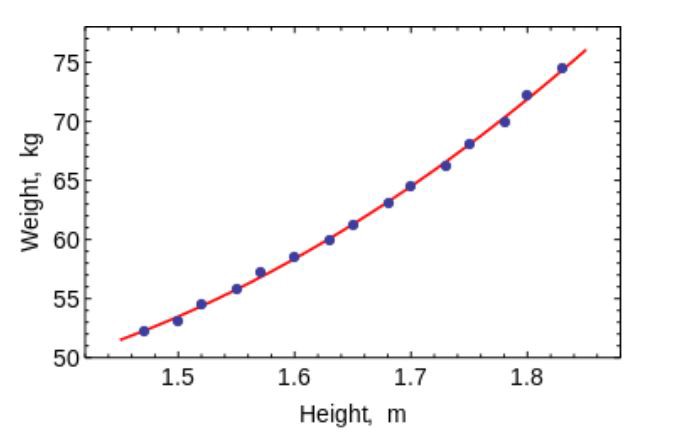
Используйте этот алгоритм, чтобы соответствовать простым кривым/регрессии.

Полезные ссылки:

• numpy.linalg.lstsq
• Numpy
• numpy.polyfit

Вводный гайд:

• Линейная регрессия от Stanford (PDF)

Ограниченная линейная регрессия

Метод наименьших квадратов может смутить выбросами, ложными полями и т. д. Нужны ограничения, чтобы уменьшить дисперсию линии, которую мы помещаем в набор данных. Правильное решение состоит в том, чтобы соответствовать модели линейной регрессии, которая гарантирует, что веса не будут вести себя “плохо”. Модели могут иметь норму L1 (LASSO) или L2 (Ridge Regression) или обе (elastic regression).



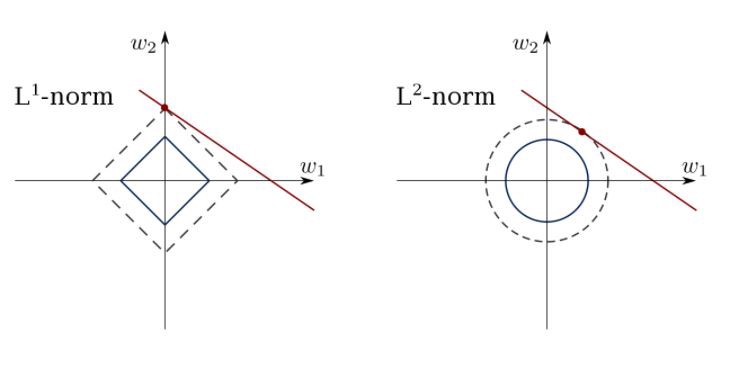
Используйте этот алгоритм для соответствия линиям регрессии с ограничениями, избегая переопределения.

Полезная ссылка:

• Обобщенные линейные модели

Вводные гайды:

• Ридж-регрессия
• LASSO регрессия

Метод k-средних

Всеми любимый неконтролируемый алгоритм кластеризации. Учитывая набор данных в виде векторов, мы можем создавать кластеры точек на основе расстояний между ними. Это один из алгоритмов машинного обучения, который последовательно перемещает центры кластеров, а затем группирует точки с каждым центром кластера. Входные данные – количество кластеров, которые должны быть созданы, и количество итераций.



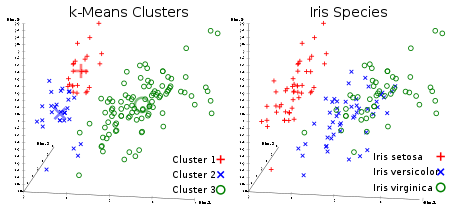
Полезная ссылка:

• sklearn.cluster.KMeans

Вводные гайды:

• Видео по кластеризации
• Введение в кластеризацию

Логистическая регрессия

Логистическая регрессия ограничена линейной регрессией с нелинейностью (в основном используется сигмоидальная функция или tanh) после применения весов, следовательно, ограничение выходов приближено к + / — классам (что равно 1 и 0 в случае сигмоида). Функции кросс-энтропийной потери оптимизированы с использованием метода градиентного спуска.

Примечание для начинающих: логистическая регрессия используется для классификации, а не регрессии. В целом, она схожа с однослойной нейронной сетью. Обучается с использованием методов оптимизации, таких как градиентный спуск или L-BFGS. NLP-разработчики часто используют её, называя “классификацией методом максимальной энтропии”.



Используйте LR для обучения простых, но очень “крепких” классификаторов.

Полезная ссылка:

• sklearn.linear_model.LogisticRegression

Вводный гайд:

• Логистическая регрессия | классификация

SVM (Метод опорных векторов)

SVM – линейная модель, такая как линейная/логистическая регрессия. Разница в том, что она имеет margin-based функцию потерь. Вы можете оптимизировать функцию потерь, используя методы оптимизации, например, L-BFGS или SGD.



Одна уникальная вещь, которую могут выполнять SVM – это изучение классификаторов классов.

SVM может использоваться для обучения классификаторов (даже регрессоров).

Полезная ссылка:

• sklearn.svm.SVC

Вводные гайды:

• Машина опорных векторов
• sklearn.linear_model.SGDClassifier

Нейронные сети прямого распространения

В основном, это многоуровневые классификаторы логистической регрессии. Многие слои весов разделены нелинейностями (sigmoid, tanh, relu + softmax и cool new selu). Также они называются многослойными перцептронами. FFNN могут быть использованы для классификации и “обучения без учителя” в качестве автоэнкодеров.



FFNN можно использовать для обучения классификатора или извлечения функций в качестве автоэнкодеров.

Полезные ссылки:

• sklearn.neural_network.MLPClassifier
• sklearn.neural_network.MLPRegressor

Вводные гайды:

• FFNN
• Автоэнкодеры

Свёрточные нейронные сети

Практически все современные достижения в области машинного обучения были достигнуты с помощью свёрточных нейронных сетей. Они используются для классификации изображений, обнаружения объектов или даже сегментации изображений. Изобретенные Яном Лекуном в начале 90-х годов, сети имеют сверточные слои, которые действуют как иерархические экстракторы объектов. Вы можете использовать их для работы с текстом (и даже для работы с графикой).



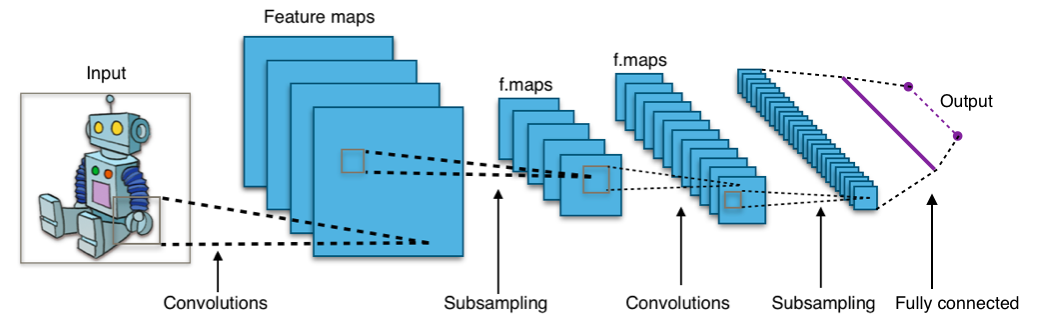
Полезные ссылки:

• Интерактивная система обучения GPU c глубоким обучением
• TorchCV: библиотека видения PyTorch имитирует ChainerCV
• ChainerCV: библиотека для глубокого обучения и компьютерного зрения
• Документация Keras

Вводные гайды:

• CNN для визуального распознавания
• Гайд для начинающих по CNN

Рекуррентные нейронные сети (RNNs)

RNNs моделируют последовательности, применяя один и тот же набор весов рекурсивно к состоянию агрегатора в момент времени t и вход в момент времени t. Чистые RNN редко используются сейчас, но его аналоги, например, LSTM и GRU являются самыми современными в большинстве задач моделирования последовательности. LSTM, который используется вместо простого плотного слоя в чистой RNN.



Используйте RNN для любой задачи классификации текста, машинного перевода, моделирования языка.

Полезные ссылки:

• Модели и примеры, созданные с помощью TensorFlow
• Бенчмарк текстовой классификации в PyTorch
• Open-Source система перевода

Вводные гайды:

• Глубокое обучение для обработки языка от Stanford
• Статьи по RNN
• Понимание LSTM

Условные случайные поля (CRFs)

Они используются для моделирования последовательности, как RNN, и могут использоваться в сочетании с RNN. Они также могут быть использованы в других задачах структурированных прогнозирования, например, в сегментации изображения. CRF моделирует каждый элемент последовательности (допустим, предложение), таким образом, что соседи влияют на метку компонента в последовательности, а не на все метки, независимые друг от друга.

Используйте CRF для связки последовательностей (в тексте, изображении, временном ряду, ДНК и т. д.).

Полезная ссылка:

• sklearn-crfsuite

Вводные гайды:

• Введение в условные случайные поля
• YouTube плейлист по условным случайным полям

Деревья принятия решений и случайные леса

Один из самых распространённых алгоритмов машинного обучения. Используется в статистике и анализе данных для прогнозных моделей. Структура представляет собой “листья” и “ветки”. На “ветках” дерева решения записаны атрибуты, от которых зависит целевая функция, в “листьях” записаны значения целевой функции, а в остальных узлах – атрибуты, по которым различаются случаи.

Чтобы классифицировать новый случай, надо спуститься по дереву до листа и выдать соответствующее значение. Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной на основе нескольких входных переменных.

Полезные ссылки:

• sklearn.ensemble.RandomForestClassifier
• sklearn.ensemble.GradientBoostingClassifier
• Документация XGBoost
• Документация CatBoost

Вводные гайды:

• Введение в деревья принятия решений
• Понимание случайных лесов: от теории до практики
• XGBoost в Python

Больше информации о машинном обучении и Data Science вы узнаете подписавшись на мой аккаунт на Хабре и Telegram-канал Нейрон. Не пропускайте будущих статей.

Всем знаний!