
По следам «Наши победили: TopCoder Open 2019» публикую задачи с трека Algorithm (классическое спортивное программирование. За полтора часа нужно решить три задачи на Java, C#, C++ или Python.)
1. Пирог на шестерых
Постановка задачи
Лимит времени — 4 секунды.
У вас есть пирог. Если смотреть сверху, пирог имеет форму (строго) выпуклого многоугольника. Вам даны координаты вершин в целых числах X и Y.
У вас есть пять друзей. Вы хотите поделить пирог на шесть частей равной площади (но не обязательно одинаковой формы). Конечно же, любой может это сделать за пять разрезов, но только профи может сделать это за три разреза.
Найдите три разрезания прямыми линиями через одну точку, которые поделят пирог на шесть равных по площади частей. Выведите {x, y, d1, d2, d3}, где (x, y) — общая точка всех трёх разрезов, а d1, d2, d3 — углы направления разрезов в радианах.
Method: cut
Parameters: int[], int[]
Returns: double[]
Method signature: double[] cut(int[] x, int[] y)
(be sure your method is public)
Примечания
- Положительное направление вдоль оси х равно 0 (радиан), положительное направление вдоль оси y равно pi/2 (радиан).
- Разрез в направлении d аналогичен разрезу в направлении pi*k+d для любого целого числа k.
- Вы можете вывести любые направления, они не обязательно должны быть от [0, pi).
- Грейдер вычислит площади ваших шести кусочков торта в doubles. Ответ будет принят, если относительная или абсолютная разница между ними меньше 10^(-4).
- Точнее, пусть X и Y будут самыми маленькими и самыми большими из ваших шести областей, вычисленных грейдером. Тогда ваш ответ будет принят, если Y <max (X+10^(-4), X*1+10^(-4))).
- (В первоначальной версии задачи использовалась точность 1e-7 вместо 1e-4. Для решения этой проблемы в архиве предел точности был снижен из-за наличия случаев вызова, которые, скорее всего, делают задачу неразрешимой с точностью 1e-7. В идеальном мире ограничения не допускают таких случаев и все еще требуют высокой точности, так что решить проблему с помощью некоторой общей числовой оптимизации непросто.)
Ограничения
- x содержит от 3 до 50 элементов включительно.
- y содержит столько же элементов, что и x.
- все координаты между 0 и 10 000 включительно
- x и y задают выпуклый многоугольник в направлении против часовой стрелки.
Problem Statement
Time limit is 4 seconds.
You have a cake. Seen from above, the cake is a (strictly) convex polygon. You are given the coordinates of its vertices in the int[]s x and y.
You have five friends. You now want to cut the cake into six pieces of equal area (but not necessarily equal shape). Of course, anyone can do that in five cuts — but only a true pro can do it in three!
Find three straight-line cuts passing through the same point that cut the cake into six equally large parts. Return {x, y, d1, d2, d3}, where (x, y) is the common point of the three cuts, and d1, d2, d3 are their directions in radians.
Definition
Class: CakeForSix
Method: cut
Parameters: int[], int[]
Returns: double[]
Method signature: double[] cut(int[] x, int[] y)
(be sure your method is public)
Notes
— The positive direction along the x axis is 0 (radians), the positive direction along the y axis is pi/2 (radians).
— A cut in direction d is the same as a cut in direction pi*k+d for any integer k.
— You may return any directions, they do not have to be from [0,pi).
— The grader will compute the areas of your six cake pieces in doubles. The answer will be accepted if the relative or absolute difference between them is less than 10^(-4).
— More precisely, let X and Y be the smallest and the largest of your six areas, as computed by the grader. Then, your answer will be accepted if Y < max( X + 10^(-4), X * (1+10^(-4)) ).
— (The original version of the problem used 1e-7 precision instead of 1e-4. For upsolving this problem in the archive the precision limit was lowered due to the existence of challenge cases that most likely make the task unsolvable with 1e-7 precision. In an ideal world the constraints would not allow such cases and still require high precision, so that it isn't easy to solve the problem via some general numeric optimization.)
Constraints
— x will have between 3 and 50 elements, inclusive.
— y will have the same number of elements as x.
— All coordinates will be between 0 and 10,000, inclusive.
— x and y will describe a convex polygon in counterclockwise order.
Примеры
0)
{0, 20, 30, 50, 30, 20}
{10, 0, 0, 10, 20, 20}
Returns:
{24.999999999437453, 9.999999999500002, 0.0, 0.7266423406817211, 2.4149503129080787 }
Симметричный, но не правильный шестиугольник. Пример ответа соответствует разрезанию его пополам по горизонтали и выполнению двух других разрезов по центру, которые разделяют каждую часть на три части.
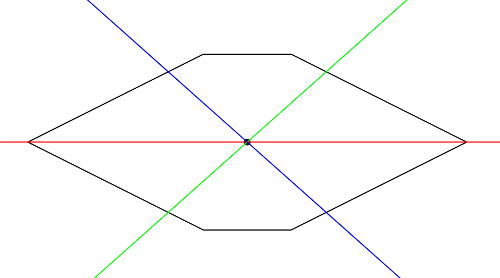
1)
{0, 1000, 0}
{0, 0, 1000}
Returns:
{333.3333333331763, 333.3333333332546, 0.7853981633986264, 2.0344439357948154, 2.6779450445891753 }
Прямоугольный треугольник. Опять же, мы можем начать с одного из трех разрезов вдоль оси симметрии.

2)
{40, 70, 90, 90, 50}
{30, 20, 40, 100, 60}
Returns:
{69.79517771922892, 52.77575974637605, 2.0616329654335885, 3.637826104091601, 4.32123485812475 }
Неправильный пятиугольник.
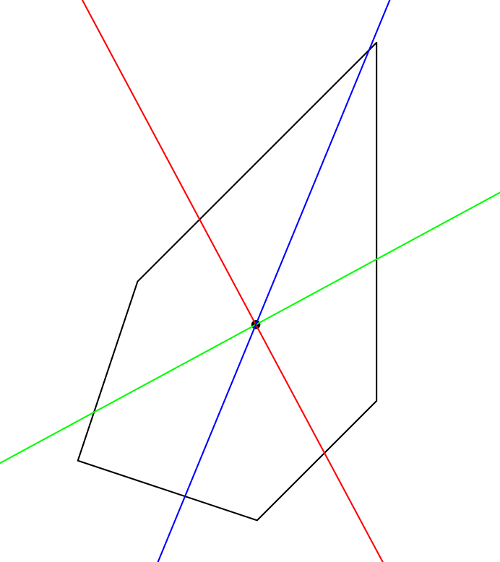
3)
{300, 400, 300, 200}
{500, 600, 700, 600}
Returns: {299.99999999974995, 599.9999999995, 0.0, 1.107148717794088, 2.034443935795705 }
Квадрат, повернутый на 45 градусов.
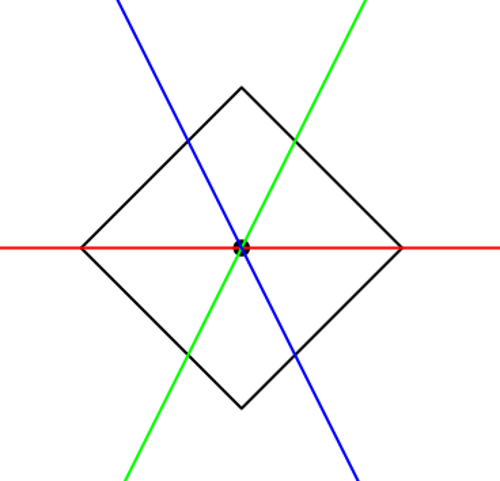
[Источник]
Комментарии (20)

tuxi
19.11.2019 16:38Если мы про пирог, а не про математику, то зачем делить сразу весь пирог? Будем отрезать по 6 одинаковых кусочков общей площадью меньше, чем половина оставшегося пирога :) Заодно решим вопрос с пирогом любой формы. Лишь бы только у него толщина была одинаковая :)

roswell
19.11.2019 17:27А в итоге всем достаётся не по куску пирога, а по кучке холодных крошек… )

MagisterLudi Автор
19.11.2019 17:30Можно размолоть в пыль и взвесить поровну.
Слышал, что так площади сложных фигур определяли: вырезали из картона и взвешивали.
Tsvetik
19.11.2019 23:15+1Так химики интегралы берут. Вырезают из тетради график и взвешивают на аналитических весах, а потом взвешивают квадратный сантиметр.

tuxi
19.11.2019 17:39А нигде не указано, что нельзя сразу съедать :) пока пережевывается предыдущий кусочек, можно отрезать следующие.

usharik
19.11.2019 19:51- Находим центр масс.
- Проводим через него линию под углом 0.
- Вращаем, пока дефект площади (S — (S1+S2)) не изменит знак на противоположный.
- Уточняем положение делением интервала пополам.
- Далее делим половину фигуры в отношение 2/3
- Потом большую часть снова пополам

BubaVV
20.11.2019 00:46Не уверен, что алгоритм сходится

usharik
20.11.2019 01:03Я тоже не уверен, но ничего лучшего пока не придумал. Почему-то кажется, что сходимость должна обеспечиваться выпуклостью многоугольника, но это не более чем догадка…
Тут еще вопрос с выбором шага для первичного поиска делящей прямой и с быстрым расчетом площади. Или формула Герона, или какое-то разбиение на треугольники.
Кстати, может авторы статьи если не решение, то пару подсказок выложат?)
BubaVV
20.11.2019 01:47Еще одна мысль. Можно разбить фигуру на треугольники и заменить каждый на точку с соответствующей массой. И примерно делить на части уже облако точек. Возможно, такая задача будет проще. Окончательно подправить положение прямых уже через расчет по пересекаемому ребру

orion76
20.11.2019 05:02Есть формула вычисления площади многугольника по координатам:
Формула площади Гаусса (формула землемера или формула шнурования или алгоритм шнурования)
т.е.
1.Можем вычислить площадь всего многоугольника.
2.Площади частей равны и вычисляются из площади исходного многоугольника.
Далее с использованием той же формулы можно составить систему уравнений.
Дополнительные «условия»:
1. Одна вершина («центр» исходной фигуры) «частей»-многоугольников общая.
2.Каждая «часть» имеет одну общую вершину с соседними частями.
3.«Зеркальные» вершины противоположных «частей» через «центр» лежат на одной прямой («линия разреза»).
4.Каждая «линия разреза» делит исходную фигуру на 2 части равной площади.
5.Все вершины частей лежат на ребрах-вершинах исходной фигуры.
Далее ищем-подбираем способ-алгоритм решения системы уравнений с необходимой точностью.
usharik
20.11.2019 12:15Вот за формулу — спасибо! Не знал про нее. Если что-то подобное узнал, то разговор был начат не зря))

Ketovdk
20.11.2019 11:27это не правда. Можно доказать при помощи квадрата, верхняя грань которого заменена на дугу, которая содержит очень много точек, но при этом почти вырожденная. Тогда центр масс будет примерно в средине верхней грани.
На самом деле все немного проще: Первую прямую проводим из любой вершины, которая бы делила пополам (можно точно в рациональных), но можно и бинпоиском (или тернарным, но лучше бинарным).
Тут есть два варианта:
1)Потом находим еще одну такую прямую, берем их точку пересечения. Это будет чем-то в духе центра такого, что любая прямая через него делит пополам. (я не уверен, что это правда, но вроде как правда. Если нет, то надежнее писать пункт 2). Далее фиксируем первую прямую, которую мы провели и ищем к ней еще две тем же самым бинпоиском так, чтобы площадь образованных сегментов составляла треть.
2) Вместо того, чтобы центр из пункта один находить пересечением двух прямых, ищем его по первой прямой бинарным поиском по минимальному ответу, образованному тремя прямыми, проходящими через этот центр.
Асимптотика: первая прямая находится за O(N), если по формуле или O(N log(MAXRAD)) бинпоиском. Вторая прямая также. Образуется точка. Еще две прямые, переходящие через эту точку каждая за O(Nlog(MAXRAD))
MAXRAD — это точность угла в радианах. Как видно из асимптотики, без особых зазрений совести ее можно поднимать хоть до 1000 бит
usharik
20.11.2019 12:17Не очень понял про квадрат и дугу. На положение центра масс не сколько количество, сколько положение точек влияет.

Ketovdk
20.11.2019 12:54представьте себе квадрат с 4мя вершинами. Центр масс в центре. А теперь замените верхнее ребро на почти вырожденную дугу, которая будет содержать 1000 вершин. Центр масс точек сместится вверх, причем полностью.

Ketovdk
20.11.2019 11:16Точнее, пусть X и Y будут самыми маленькими и самыми большими из ваших шести областей, вычисленных грейдером. Тогда ваш ответ будет принят, если Y <max (X+10^(-4), X*1+10^(-4)))
Почему неразрешимой? Можно же просто поднять точность до 256 (ну или 128) битового формата и разницы в решении нет никакой

GarryC
20.11.2019 11:59Легко доказать, что при проведении любых двух линий через центр масс площадь отсекаемых ими кусков одинакова — дальше легко.
Площадь сегмента считает через сумму его треугольников и останется поделить последний треугольник для получения необходимо остатка — тут тригонометрия потребуется.
Ну это, конечно, только идея решения, само решение я за 10 минут не напишу.


Tsvetik
По-видимому все линии проходят через центр масс. Первая линия проводится произвольно и делит многоугольник пополам. А две оставшиеся так, чтобы они отсекали треть площади. Но это не точно
vladimirad
Центр масс и задачу можно решать для трехмерного случая тоже.