Будь вы новичок в работе с данными или, напротив, матёрый профессионал, вам никуда не деться от работы с различными видами расстояний (так же называемых «метриками»).

Ниже разобраны три базовых метрики, с которыми вам рано или поздно придётся столкнуться.

1. Евклидово расстояние (расстояние по прямой линии)

Из всех расстояний Евклидово самое простое для восприятия: именно его мы интуитивно представляем в первую очередь, когда кто-то просит нас оценить дистанцию.

Евклидова метрика — это прямая линия между двумя точками с заданными координатами X и Y. Двух координат (широты и долготы) нам, в свою очередь, достаточно, чтобы однозначно указать объект на карте.

Рассмотрим часть условного города:

Для расчёта Евклидова расстояния между точками A и B нам понадобятся лишь их координаты (Xn, Yn) и формула из теоремы Пифагора.

Теорема говорит нам о том, как рассчитать длину гипотенузы ( c ) прямоугольного треугольника, зная длины его катетов (a и b): a? + b? =c?. Таким образом:

2. Расстояние L1 (расстояние городских кварталов)

Расстояние L1 так же известное как расстояние городских кварталов, манхеттенское расстояние, метрика прямоугольного города, метрика городского квартала или метрика такси измеряет дистанцию не по прямой, а блоками.

Картинка ниже показывает, как это работает:

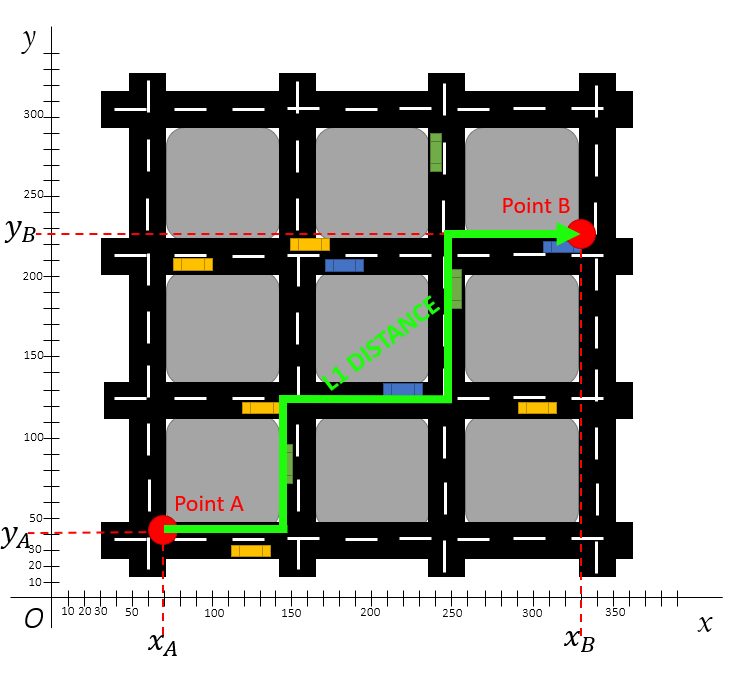
В отличие от Евклидова, в расстоянии L1 не один, а несколько кратчайших путей из точки A в точку B. Например, можно сначала пойти на два блока вверх и на три вправо после.

Но L1 — расстояние, поэтому конкретная траектория для расчётов не важна. Важно лишь знать, сколько блоков нужно пройти на север и сколько на восток. Сумма их расстояний и будет нашей метрикой.

3. Расстояние Чебышёва (метрика шахматной доски)

Расстояние Чебышёва иногда называют L-бесконечность метрикой («L Infinity Distance»). Легче всего понять как она работает, если представить движение короля по шахматной доске: он может передвигаться во всех направлениях: вперёд, назад, влево, вправо и по диагонали.

Главное отличие от расстояния L1 в том, как считается движение по диагонали: это два шага в L1 (один вправо + один вверх), но всего один шаг в расстоянии Чебышёва.

Обе метрики в свою очередь отличаются от Евклидовой, где движение по диагонали займёт корень из двух шагов (т.е. примерно 1,41):

Слева направо: дистанции в Евклидовой метрике, L1 метрике, метрике Чебышёва.

Другим примером расстояния Чебышёва будет движение квадрокоптера с двумя независимыми моторами: один, чтобы лететь вперёд-назад, второй, чтобы вправо-влево. Оба мотора могут работать одновременно на максимальной мощности.

Тогда движение по диагонали (если оба мотора включены) займёт столько же времени, сколько движение по горизонтали или вертикали (если включен только один соответствующий мотор).

Можно догадаться, что расстояние Чебышёва определяется как наибольшая дистанция по одной из осей.

---

Надеюсь, эта статья открыла для вас что-то новое или, напротив, помогла освежить знания. Удачи в применении метрик на практике!