24.04.2020 06:53
Neoprog 30 3300 Источник

Всем привет! В результате перехода на удаленную работу у меня появилось больше свободного времени на разработку гексапода (+2 часа в день за счет экономии на дороге). Я наконец-то смог сделать универсальный алгоритм для построения траектории движения в реальном времени. Новая математика позволила реализовать базовые движения путем изменения всего двух параметров. Это очередной шаг к внедрению «автопилота». В этой статье я постараюсь подробно рассказать о новой математике и как это вообще работает. Будет много картинок и gif.

Этапы разработки:

Часть 1 — проектирование
Часть 2 — сборка
Часть 3 — кинематика
Часть 4 — математика траекторий и последовательности
Часть 5 — электроника
Часть 6 — переход на 3D печать
Часть 7 — новый корпус, прикладное ПО и протоколы общения
Часть 8 — улучшенная математика передвижения

Назад во времени


До этого момента все базовые движения (вперед, назад, поворот) задавались в виде «перемести ногу из текущей позиции в точку (X, Y, Z), используя линейное/синусоидальное/какое-нибудь перемещение». Это работает достаточно хорошо и надежно, но сильно ограничивает в движении. Например, чтобы реализовать движение по дуге с радиусом R1 нужно заранее рассчитать координаты начала и окончания движения для каждой конечности, добавить дополнительную кнопку в приложение, чтобы можно было выбрать это движение. Соответственно для добавления движения по дуге с другим радиусом R2, нужно опять рассчитать координаты и добавить еще одну кнопку. Крайне неудобно.

Сейчас для реализации базовых движений используется один математический блок, который можно адаптировать под различные ситуации двумя параметрами. Главным бонусом новой математики стала поддержка движения по дуге с изменением её радиуса прямо во время движения!

Идея алгоритма


Для начала стоит объяснить на пальцах как это работает. Что будет, если выбрать на окружности окно фиксированного размера и начать увеличивать её радиус? Вот что:


Всё просто правда? Изменяя радиус окружности мы можем получить различные траектории движения и с некоторой точность прямую линию. На этом можно было и остановиться, но не все так радужно. Нельзя просто взять и реализовать это на основе одного только радиуса — есть нюансы.

Начальные положения конечностей гексапода могут находиться на разных окружностях, соответственно параметры уравнения уже будут другими. В моем случае конечности располагаются следующим образом (примерно):


Значение расстояния, которое должна пройти конечность зависит от радиуса окружности, на которой она находится. Это заставляет переходить к индивидуальному расчету траектории для каждой конечности. Для решения этой проблемы необходимо найти окружность с максимальным радиусом, рассчитать начальный и конечный углы дуги. Дальше относительно полученной дуги находятся дуги для других конечностей. Я сделал анимацию работы данного куска алгоритма:


Есть анимация для наглядности работы всей этой магии (как же я рад что в наше время есть Excel). В начале изменяется значение расстояния, которое должен пройти гексапод за цикл (аналогично скорости), затем изменяется значение кривизны траектории (аналогично повороту руля).


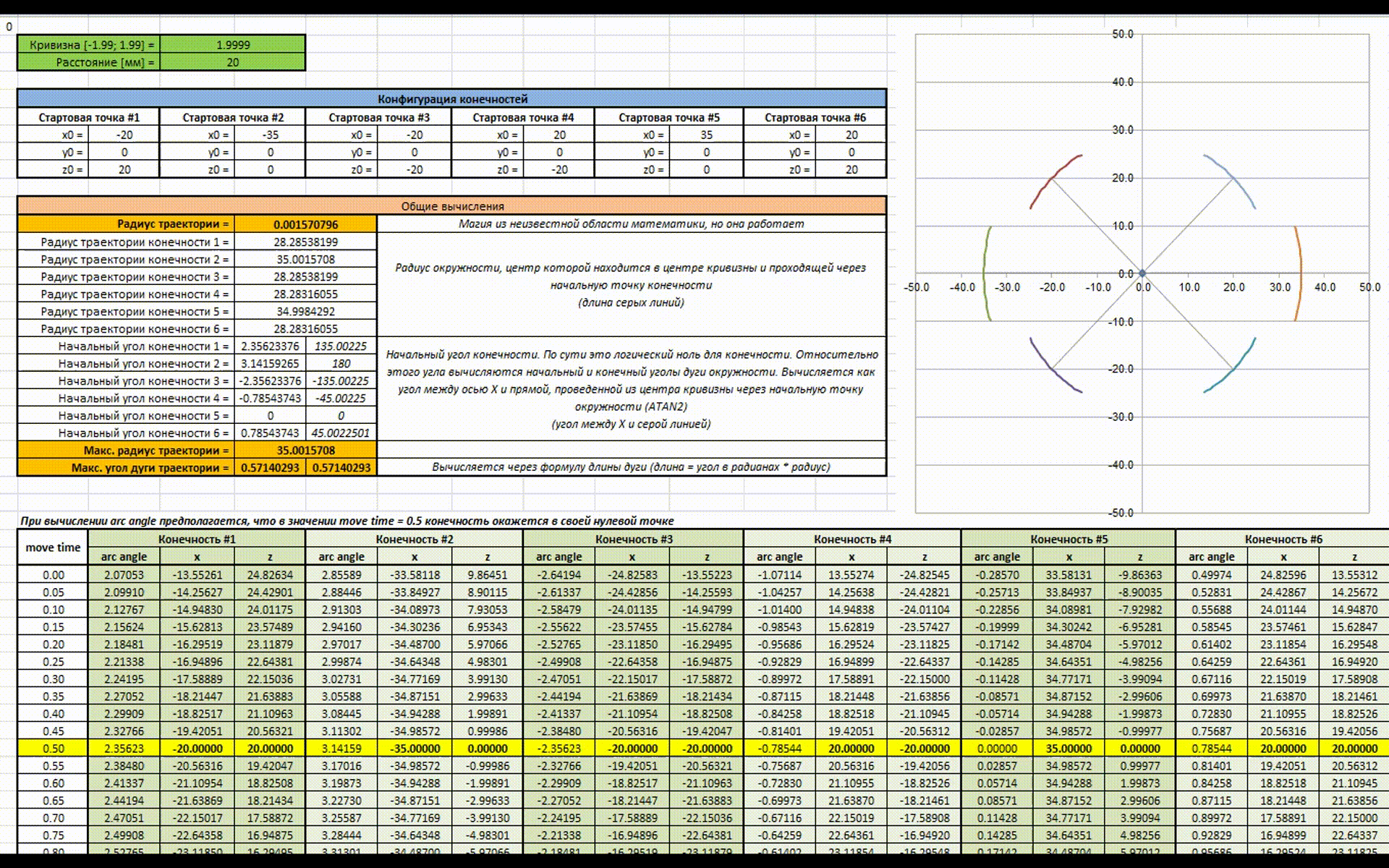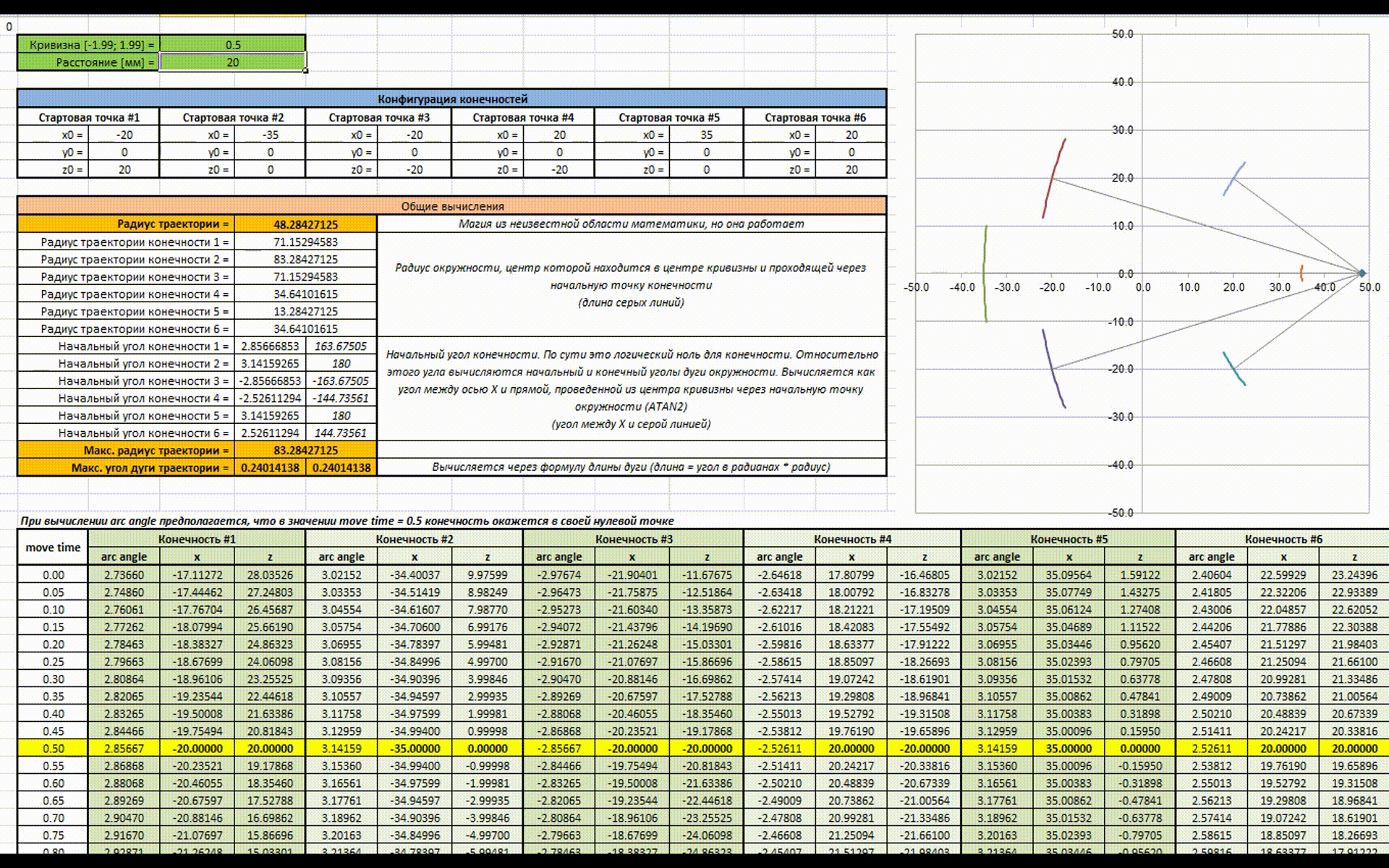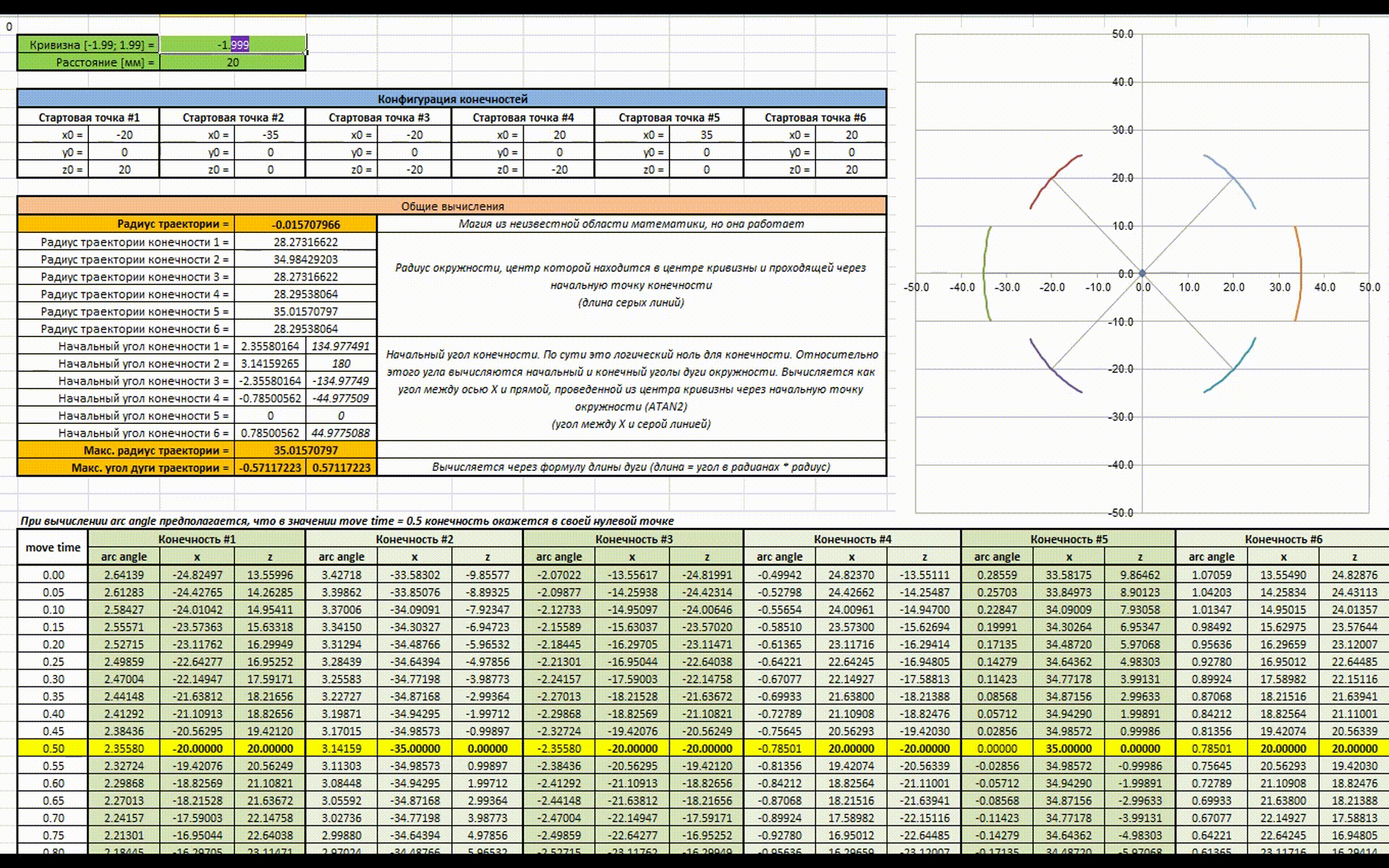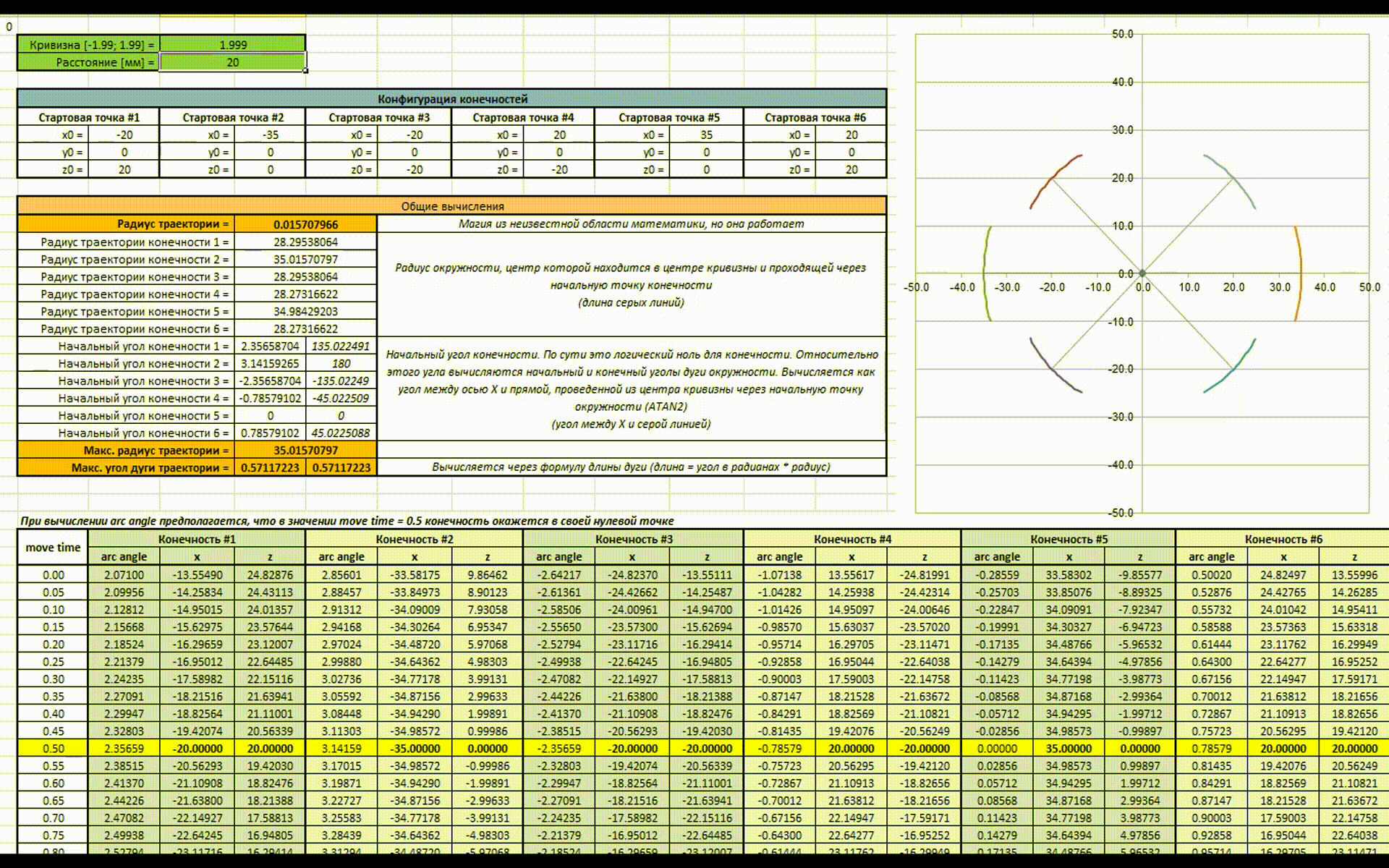
В целом в этом и заключается идея новой математики, надеюсь получилось доступно объяснить. Теперь можно разобрать алгоритм подробнее и попробовать посчитать все руками на практике.

Математика


Входные параметры


Переменными входными параметрами являются расстояние (distance) и кривизна траектории движения (curvature). Значение кривизны траектории должно находится в диапазонах [-1.999; -0.001] и [0.001; 1.999], в то время как максимальное значение расстояния зависит от физических характеристик гексапода. В моем случае максимальное расстояние за цикл равно 110мм, при больших значениях конечности начинают упираться в друг друга. Для примера расчета возьмем значения curvature = 1.5 и distance = 20.

Так же для работы алгоритма необходимо знать начальные положения конечностей. Это точки, в которых находятся конечности, когда гексапод встал на ноги. Для примера будем использовать следующие точки (начало координат каждой конечности находится в месте крепления COXA):


Note: Я работаю в плоскости XZ и на координату Y можно не обращать внимания. Ознакомиться с системой координат гексапода можно в третьей части цикла

В итоге мы имеем следующее:

Формулы и расчеты


Начнем с расчета координат центра движения гексапода в зависимости от значения кривизны и расстояния:

$R = tg(\frac{(2 - curvature) * \Pi}{4}) * distance$

$R = tg(\frac{(2 - 1.5) * \Pi}{4}) * 20 = 8.28$

В итоге мы получили точку [R; 0] и траекторию движения тела гексапода. Относительно нее будут рассчитываться траектории для каждой конечности.


Далее необходимо вычислить радиусы траекторий для каждой конечности относительно центра движения (точки [R; 0]) c учетом начального положения конечности [x0; z0]. Более понятным языком — найти длину вектора, проведенного из точки [R; 0] в точку [x0; z0]:

$R_i = \sqrt{(R - x_{0i})^2 + z_{0i}^2}$

$R_0 = \sqrt{(8.28 - (-20))^2 + 20^2} = 34.64$

$R_1 = \sqrt{(8.28 - (-35))^2 + 0^2} = 43.28$

$R_2 = \sqrt{(8.28 - (-20))^2 + (-20)^2} = 34.64$

$R_3 = \sqrt{(8.28 - 20)^2 + (-20)^2} = 23.17$

$R_4 = \sqrt{(8.28 - 35)^2 + 0^2} = 26.71$

$R_5 = \sqrt{(8.28 - 20)^2 + 20^2} = 23.17$


Картинка для наглядности. Синим показаны нужные вектора.


Находим из полученных значений максимальное:

$R_{max} = maximum(R_{0-5})$

$R_{max} = 43.28$


Дальше нужно найти угол для каждого вектора, которые мы пытали в предыдущем шаге.

$\alpha_{0i} = atan2(z_{0i}; -(R - x_{0i}))$

$\alpha_{00} = atan2(20; -(8.28 - (-20))) = 2.52 (144.7°)$

$\alpha_{01} = atan2(0; -(8.28 - (-35))) = 3.14 (180°)$

$\alpha_{02} = atan2(-20; -(8.28 - (-20))) = -2.52 (-144.7°)$

$\alpha_{03} = atan2(-20; -(8.28 - 20)) = -1.04 (-59.6°)$

$\alpha_{04} = atan2(0; -(8.28 - 35)) = 0 (0°)$

$\alpha_{05} = atan2(20; -(8.28 -20)) = 1.04 (59.6°)$


Теперь находим угол дуги на самой большой окружности радиуса R_maх (самой удаленной от центра движения траектории), длина которой должна быть равна значению distance. Этот угол определяет начальные и конечные углы других дуг, по которым будут двигаться конечности. Думаю картинка ниже поможет понять это.


Угол вычисляется следующим образом:

$arcMax = sign(R) * \frac{distance}{R_{max}}$

$arcMax = \frac{20}{43.28} = 0.462 (26°)$


Дальше используя этот угол мы можем вычислить начальные и конечные углы дуг для других конечностей. Как то так это должно получиться:


Небольшое отступление. Для реализации этого алгоритма необходимо ввести понятие времени, значение которого лежит в диапазоне [0; 1]. Так же необходимо, чтобы каждая конечность при значении времени 0.5 возвращалась в свою начальную точку. Данное правило является проверкой корректности расчетов — все окружности должны проходить через начальные точки каждой конечности.

Дальше начинается вычисление точек по полученным параметрам дуг, используя следующие формулы:

$arcAngle_i = (time - 0.5) * \alpha_{0i} + arcMax$

$x_i = R + R_i * cos(arcAngle_i)$

$z_i = R_i * sin(arcAngle_i)$


Исходный код функции


static bool process_advanced_trajectory(float motion_time) {

    // Check curvature value
    float curvature = (float)g_current_trajectory_config.curvature / 1000.0f;
    if (g_current_trajectory_config.curvature == 0)    curvature = +0.001f;
    if (g_current_trajectory_config.curvature > 1999)  curvature = +1.999f;
    if (g_current_trajectory_config.curvature < -1999) curvature = -1.999f;
    
    //
    // Calculate XZ
    //
    float distance = (float)g_current_trajectory_config.distance;

    // Calculation radius of curvature
    float curvature_radius = tanf((2.0f - curvature) * M_PI / 4.0f) * distance;

    // Common calculations
    float trajectory_radius[SUPPORT_LIMBS_COUNT] = {0};
    float start_angle_rad[SUPPORT_LIMBS_COUNT] = {0};
    float max_trajectory_radius = 0;
    for (uint32_t i = 0; i < SUPPORT_LIMBS_COUNT; ++i) {
        
        float x0 = g_motion_config.start_positions[i].x;
        float z0 = g_motion_config.start_positions[i].z;

        // Calculation trajectory radius
        trajectory_radius[i] = sqrtf((curvature_radius - x0) * (curvature_radius - x0) + z0 * z0);

        // Search max trajectory radius
        if (trajectory_radius[i] > max_trajectory_radius) {
            max_trajectory_radius = trajectory_radius[i];
        }

        // Calculation limb start angle
        start_angle_rad[i] = atan2f(z0, -(curvature_radius - x0));
    }
    if (max_trajectory_radius == 0) {
        return false; // Avoid division by zero
    }

    // Calculation max angle of arc
    int32_t curvature_radius_sign = (curvature_radius >= 0) ? 1 : -1;
    float max_arc_angle = curvature_radius_sign * distance / max_trajectory_radius;

    // Calculation points by time
    for (uint32_t i = 0; i < SUPPORT_LIMBS_COUNT; ++i) {
        
        // Inversion motion time if need
        float relative_motion_time = motion_time;
        if (g_motion_config.time_directions[i] == TIME_DIR_REVERSE) {
            relative_motion_time = 1.0f - relative_motion_time;
        }

        // Calculation arc angle for current time
        float arc_angle_rad = (relative_motion_time - 0.5f) * max_arc_angle + start_angle_rad[i];

        // Calculation XZ points by time
        g_limbs_list[i].position.x = curvature_radius + trajectory_radius[i] * cosf(arc_angle_rad);
        g_limbs_list[i].position.z = trajectory_radius[i] * sinf(arc_angle_rad);
        
        // Calculation Y points by time
        if (g_motion_config.trajectories[i] == TRAJECTORY_XZ_ADV_Y_CONST) {
            g_limbs_list[i].position.y = g_motion_config.start_positions[i].y;
        }
        else if (g_motion_config.trajectories[i] == TRAJECTORY_XZ_ADV_Y_SINUS) {
            g_limbs_list[i].position.y = g_motion_config.start_positions[i].y;
            g_limbs_list[i].position.y += LIMB_STEP_HEIGHT * sinf(relative_motion_time * M_PI);  
        }
    }
    
    return true;
}

Тут я решил показать еще и расчет Y координаты (Calculation Y points by time). Расчет зависит от выбранной траектории, которая задана в коде жестко и необходима для реализации движения конечности по земле и по воздуху.

Так же имеется кусок для реализации обратного направления движения (Inversion motion time if need). Он нужен, чтобы во время движения трех конечностей по земле, другие три конечности двигались в обратном направлении по воздуху.

Результаты