Формализуем задачу. Нам требуется функция drawEllipse(coords, sizes, vector), где:
- coords — координаты центра эллипса — массив [x, y]
- sizes — длины большой и малой полуосей эллипса — массив [a, b]
- vector — вектор [x, y] наклона эллипса
В статье приведено три способа решения данной задачи.
В качестве первого метода были выбраны кривые Безье. Для построения такой кривой требуются четыре точки: начальная, конечная и две контрольные.
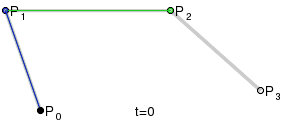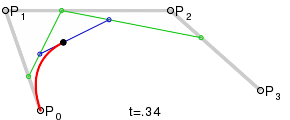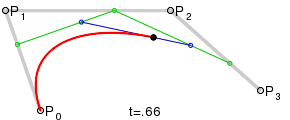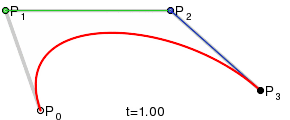
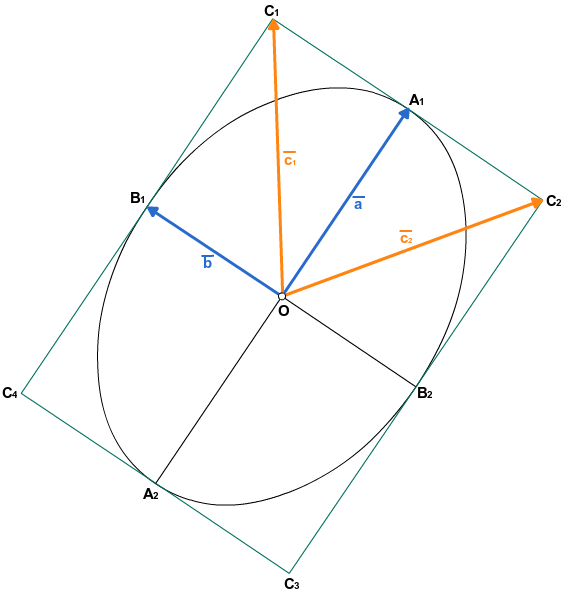
Искомый эллипс будет состоять из двух таких кривых, причем нетрудно догадаться, что вышеупомянутые точки у каждой из них будут вершинами прямоугольника. Давайте исследуем наш эллипс.
- Имеем некоторый вектор

Найдем единичный вектор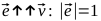
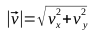
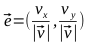
Найдем единичный вектор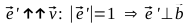
Для этого вспомним свойство скалярного произведения векторов обращаться в ноль в случае, если они перпендикулярны: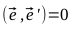
Таким образом: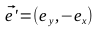
- Найдем векторы
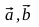 , точки A1, A2, B1, B2
, точки A1, A2, B1, B2
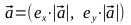
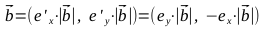

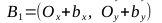
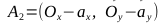
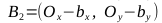
- Найдем векторы
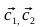 , точки C1, C2, C3, C4
, точки C1, C2, C3, C4
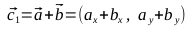
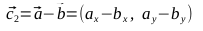
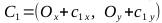
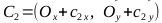
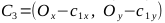
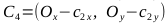
- Вспомним, что для рисования эллипса нам нужны две кривые Безье:
- 1-я имеет начальную точку B1, конечную B2, проходит через точку A1
- 2-я имеет начальную точку B2, конечную B1, проходит через точку A2
Изобразим момент построения кривой Безье в точке, в которой она (кривая) будет наиболее близка к отрезку между контрольными точками. В нашем случае это будет выглядеть так:
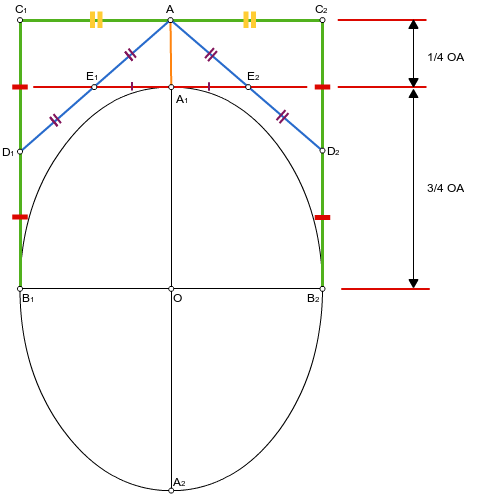
Из рисунка очевидно, что расстояние от этой точки (A1) до отрезка между контрольными точками (C1, C2) будет составлять четверть от расстояния между центром искомого эллипса (O) и тем же отрезком (C1, C2), то есть:
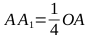
- Обозначим ОА через x. Решим уравнение
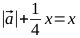
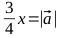
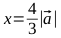
Таким образом, для получения эллипса с нужными параметрами нам необходимо умножить вектор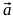 на параметр
на параметр 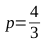 , после чего вернуться к вычислениям, описанным в пунктах 1-4. В результате получаем наборы точек (B1, C1, C2, B2 и B2, C3, C4, B1) для построения двух кривых Безье, вместе представляющих искомую фигуру.
, после чего вернуться к вычислениям, описанным в пунктах 1-4. В результате получаем наборы точек (B1, C1, C2, B2 и B2, C3, C4, B1) для построения двух кривых Безье, вместе представляющих искомую фигуру.
Собственно демо и код:
function drawEllipse(ctx, coords, sizes, vector) {
var vLen = Math.sqrt(vector[0]*vector[0]+vector[1]*vector[1]); // вычисляем длину вектора
var e = [vector[0]/vLen, vector[1]/vLen]; // единичный верктор e || vector
var p = 4/3; // параметр
var a = [e[0]*sizes[0]*p, e[1]*sizes[0]*p]; // находим вектор a, используя параметр
var b = [e[1]*sizes[1], -e[0]*sizes[1]]; // находм вектор b
// находим точки A1, B1, A2, B2
var dotA1 = [coords[0]+a[0], coords[1]+a[1]];
var dotB1 = [coords[0]+b[0], coords[1]+b[1]];
var dotA2 = [coords[0]-a[0], coords[1]-a[1]];
var dotB2 = [coords[0]-b[0], coords[1]-b[1]];
// находим вектора c1, c2
var c1 = [a[0]+b[0], a[1]+b[1]];
var c2 = [a[0]-b[0], a[1]-b[1]];
// находим точки C1, C2, C3, C4
var dotC1 = [coords[0]+c1[0], coords[1]+c1[1]];
var dotC2 = [coords[0]+c2[0], coords[1]+c2[1]];
var dotC3 = [coords[0]-c1[0], coords[1]-c1[1]];
var dotC4 = [coords[0]-c2[0], coords[1]-c2[1]];
// рисуем наш эллипс
ctx.strokeStyle = 'black';
ctx.beginPath();
ctx.moveTo(dotB1[0], dotB1[1]); // начальная точка
ctx.bezierCurveTo(dotC1[0], dotC1[1], dotC2[0], dotC2[1], dotB2[0], dotB2[1]); // рисуем кривую Безье
ctx.bezierCurveTo(dotC3[0], dotC3[1], dotC4[0], dotC4[1], dotB1[0], dotB1[1]); // и вторую из точки, где закончили рисовать первую
ctx.stroke();
ctx.closePath();
// возвращаем вектору a изначальную длину
a = [e[0]*sizes[0], e[1]*sizes[0]];
// отрисовываем красным большую и малую оси эллипса, чтобы проверить, правильно ли мы отобразили запрошенный эллипс
ctx.beginPath();
ctx.moveTo(coords[0]+a[0], coords[1]+a[1]);
ctx.lineTo(coords[0]-a[0], coords[1]-a[1]);
ctx.moveTo(coords[0]+b[0], coords[1]+b[1]);
ctx.lineTo(coords[0]-b[0], coords[1]-b[1]);
ctx.strokeStyle = 'red';
ctx.stroke();
ctx.closePath();
}

Upd. Ознакомившись с комментариями, написал функцию рисования эллипса через параметрическое уравнение, и оказалось, что фигура, которая получается с помощью кривых Безье не вполне точно совпадает с эллипсом. На наложении фигур видно, что нарисованный кривыми Безье объект (красный) местами шире, чем правильный эллипс (синий). Вот демо наложения фигур.

function drawEllipseParam(ctx, coords, sizes, angle, segments) {
ctx.save();
ctx.translate(coords[0], coords[1]);
ctx.rotate(angle);
ctx.beginPath();
var x, y, firstTime=true;
var dt = 2*Math.PI/segments;
for(var t=0; t<2*Math.PI; t+=dt) {
x = sizes[0]*Math.cos(t);
y = sizes[1]*Math.sin(t);
if(firstTime) {
firstTime = false;
ctx.moveTo(x, y);
} else {
ctx.lineTo(x, y);
}
}
ctx.strokeStyle = 'blue';
ctx.stroke();
ctx.closePath();
ctx.restore();
}
Upd. В комментариях подсказали более нативный и простой способ отрисовки наклонного эллипса (спасибо subzey). Оставлю здесь, чтобы не затерялся. Вот демо.
function drawEllipse(ctx, coords, sizes, angle) {
ctx.beginPath();
ctx.save(); // сохраняем стейт контекста
ctx.translate(coords[0], coords[1]); // перемещаем координаты в центр эллипса
ctx.rotate(angle); // поворачиваем координатную сетку на нужный угол
ctx.scale(1, sizes[1]/sizes[0]); // сжимаем по вертикали
ctx.arc(0, 0, sizes[0], 0, Math.PI*2); // рисуем круг
ctx.restore(); // восстанавливает стейт, иначе обводка и заливка будут сплющенными и повёрнутыми
ctx.strokeStyle = 'green';
ctx.stroke(); // обводим
ctx.closePath();
}
Комментарии (23)

eocron
10.04.2015 17:31Извините, но не до конца понял, чем Вам не понравилось параметрическое уравнение и отрисовка через какое то dt?
Почему было решено все делать через кривые безье?
Smoren Автор
10.04.2015 17:37Я думал и о таком варианте решения, но решил остановиться на кривых Безье, потому что раньше с ними не работал.

eocron
10.04.2015 17:45+1А, хорошо ) просто это не совсем эллипс, скорее визуальная аппроксимация, так как Безье это все таки полином. Но это так, придирки к названию )

Aingis
10.04.2015 17:53Ага, а разница между полокружностью и привой Безье уже довольно заметна. Лучше брать 1/3 или 1/4, как это обычно делают. (Эллипс — всего лишь вытянутая окружность.)

Smoren Автор
10.04.2015 19:21И правда. Написал функцию рисования эллипса через параметрическое уравнение. Наложил. Разница заметна. jsfiddle.net/Smoren/ztpy8pag
function drawEllipseParam(ctx, coords, sizes, angle, segments) { ctx.save(); ctx.translate(coords[0], coords[1]); ctx.rotate(angle); ctx.beginPath(); var x, y, firstTime=true; var dt = 1/segments; for(var t=0; t<2*Math.PI; t+=dt) { x = sizes[0]*Math.cos(t); y = sizes[1]*Math.sin(t); if(firstTime) { firstTime = false; ctx.moveTo(x, y); } else { ctx.lineTo(x, y); } } ctx.strokeStyle = 'blue'; ctx.stroke(); ctx.closePath(); ctx.restore(); }

kahi4
10.04.2015 17:37+4А можно проще:
ctx.rotate(0.3); ctx.save(); ctx.translate(50, 50); ctx.scale(0.75, 1); ctx.arc(0, 0, 50, 0, Math.PI*2, false); ctx.closePath(); ctx.stroke(); ctx.restore(); ctx.rotate(-0.3);
Demo: jsfiddle.net/2frckjxm
mospans
10.04.2015 18:31В этом случае линия контура может стать слишком тонкой. Чтобы стало заметно, попробуйте использовать:
ctx.scale(0.1, 1);

Keyten
11.04.2015 20:13Хм
Прочитал пост в метро, но не имел возможности написать, а сейчас уже все доступные способы описали и реализовали :). И через scale, и аппроксимацию отрезками.
Добавлю, разве что, вот эту ссылку
stackoverflow.com/questions/2172798/how-to-draw-an-oval-in-html5-canvas/23184724
Это автору топа.
Теперь конкретно к вам, kahi4. Мне больше нравится вот так :).
ctx.save(); ctx.fillStyle = 'red'; ctx.translate(100, 100); ctx.rotate(30 * Math.PI / 180); ctx.scale(0.75, 1); ctx.translate(-100, -100); ctx.arc(100, 100, 50, 0, Math.PI*2, true); ctx.fill(); ctx.restore();

Zenitchik
10.04.2015 21:02Я в своё время пробовал. Но не сумел добиться, чтобы у меня эллипс и дуга такого же эллипса точно друг на друга накладывались (нужно было выделить более жирно часть эллиптической орбиты). В результате я плюнул и стал строить орбиты как графики функций.

subzey
11.04.2015 13:12+3Не нужно велосипедов! Всё это можно сделать встроенными средствами: jsfiddle.net/7ppu4g9x

Zenitchik
13.04.2015 19:16Вот как раз этот метод мне и дал разные результаты для целого эллипса и его дуги.

subzey
13.04.2015 19:56Как по мне, эллипс и дуга вполне достойно стыкуются: jsfiddle.net/subzey/p0pq6gr8
По границам жёлтого отрезка есть сероватые полосы, но это из-за субпиксельного рендеринга — если нарисовать две линии поверх друг друга, не попадая в пиксели, получится тот же эффект.
Zenitchik
13.04.2015 20:07У меня была орбита толщиной один пиксель и, собственно, рабочий участок — два пикселя. Не утверждаю, что нельзя найти решение, но мне перейти к графику уравнения оказалось технически проще, потому что так уже строились гиперболы.

subzey
13.04.2015 20:30Вас понял. Вашем случае действительно рисование по точкам весьма и весьма приемлимый подход.



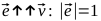
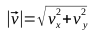
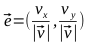
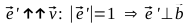
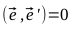
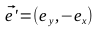
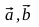 , точки A1, A2, B1, B2
, точки A1, A2, B1, B2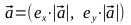
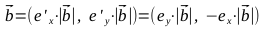

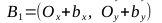
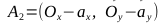
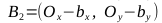
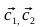 , точки C1, C2, C3, C4
, точки C1, C2, C3, C4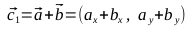
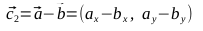
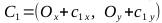
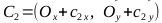
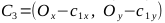
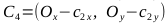

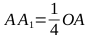
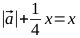
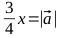
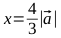
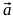 на параметр
на параметр 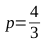 , после чего вернуться к вычислениям, описанным в пунктах 1-4. В результате получаем наборы точек (B1, C1, C2, B2 и B2, C3, C4, B1) для построения двух кривых Безье, вместе представляющих искомую фигуру.
, после чего вернуться к вычислениям, описанным в пунктах 1-4. В результате получаем наборы точек (B1, C1, C2, B2 и B2, C3, C4, B1) для построения двух кривых Безье, вместе представляющих искомую фигуру.

GreatRash
А если мы сидим на движке Хрома (собссно Chrome или Opera), то можно заюзать экспериментальную фичу:
ctx.ellipse(x, y, radiusX, radiusY, rotation, startAngle, endAngle, anticlockwise);
Smoren Автор
спасибо за совет!