Изобретаем велосипед или пишем персептрон на C++. Часть 3
Реализуем обучение многослойного персептрона на C++ при помощи метода обратного распространения ошибки.

Предисловие
Всем привет!) Перед тем, как мы приступим к основе этой статьи, хочется сказать несколько слов о предыдущих частях. Предложенная мной реализация — это издевательство над оперативной памятью компьютера, т.к. трёхмерный вектор насилует память обилием пустых ячеек, на которые тоже резервирована память. Поэтому способ далеко не самый лучший, но, надеюсь, он поможет понять начинающим программистам в этой области, что находится «под капотом» у самых простых нейросетей. Это раз. Описывая активационную функцию в первой части, я допустил ошибку — активационная функция не обязательно должна иметь ограничения по области значений. Всё это зависит от целей программиста. Единственное условие — функция должна быть определена на всей числовой оси. Это два
Введение
Так-с, а теперь ближе к теме. Сегодня мы реализуем backpropagation — метод для корректировки весовых коэффициентов сети. Итак, приступим!
Ссылка на предыдущие две статьи: habr.com/ru/post/514372
Немного математики
Я наткнулся на классную статью по backpropagation — ссылка.
В этой статье всё хорошо расписано, поэтому я, в основном, буду повествовать о использовании тех методов в своём коде.
Вкратце объясню принцип метода на вот такой сети:
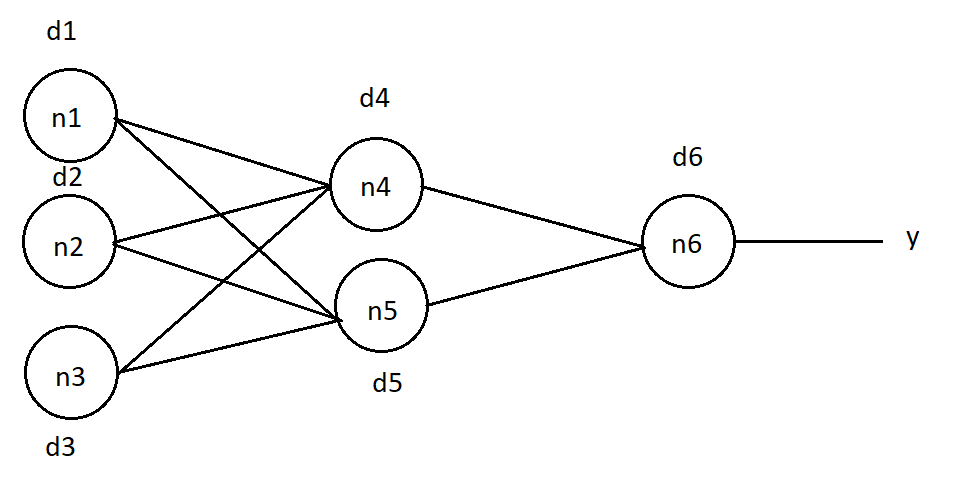
Постараюсь правильно передать смысл обучения этим способом, но если что, то поправьте в комментариях. Итак, чтобы обучить сеть, мы должны изменить значения весовых коэффициентов. Причём, изменение веса связи прямо пропорционально ошибке, которую даёт соответствующий нейрон. В той статье ошибка определяется так: (1), где j — номер элемента, для которого вычисляем ошибку, k — номер слоя, от которого пришла ошибка, т.е. слоя правее на нашей сети.
Начнём вычислять ошибку каждого нейрона, идём с конца. Пусть на выходе сети мы ожидаем значение "O". Тогда для нейрона n6 ошибка составляет d6 = (O — y)*( f(in) )*(1 — f(in) ) (2), где in — входное значение в
элемент n6, f(in) — значение активационной функции от этого входного значения.
Теперь исходя из формулы (1), рассчитываем ошибки для нейронов слоя слева. Для n4 ошибка выглядит так:
d4 = d6 * w46 *( f(in4) ) * (1 — f(in4)), где w46 — вес связи между n4 и n6, in4 — входное значение нейрона n4.
d5 = d6 * w56 *( f(in5) ) * (1 — f(in5)), для n5.
d1 = (d4 * w14 + d5 * w15) *( f(in1) ) * (1 — f(in1)), а вот так выглядит ошибка нейрона n1, у него ведь не одна связь, а две — поэтому мы вносим в формулу ещё ошибку второй связи.
Тогда для n2 и n3 ошибки выглядят соответственно:
d2 = (d4 * w24 + d5 * w25) *( f(in2) ) * (1 — f(in2))
d3 = (d4 * w34 + d5 * w35) *( f(in3) ) * (1 — f(in3))
А сейчас, наконец, рассчитаем корректировку весов:
?w46 = d6 * A * f(in4), w46 — вес связи n4 и n6 нейрона, а f(in4) — значение активационной функции от входного значения нейрона n4, A — коэффициент скорости обучения обучения, чем он ближе к нулю — тем сеть медленнее, но точнее обучается.
?w56 = d6 * A * f(in5), соответственно корректировка связи элементов n5 и n6.
Составим корректировки для остальных связей:
?w14 = d4 * A * f(in1)
?w24 = d4 * A * f(in2)
?w34 = d4 * A * f(in3)
?w15 = d4 * A * f(in1)
?w25 = d4 * A * f(in2)
?w35 = d4 * A * f(in3)
Видите закономерность? Именно она и поможет в написании функции обучения. Тогда переходим к этому этапу.
Пишем код
Особые моменты функции будем рассматривать подробнее
void NeuralNet::learnBackpropagation(double* data, double* ans, double acs, double k) { //data - массив обучающих данных, ans - массив ответов на обучающие данные, k - количество эпох обучения, acs- скорость обученияДалее идёт цикл, отсчитывающий кол-во итераций обучения:
for (uint32_t e = 0; e < k; e++) {
double* errors = new double[neuronsInLayers[numLayers - 1]]; //объявим массив для хранения ошибок выходного слоя
//Шуточное "Do_it" было заменено на "Forward"
Forward(neuronsInLayers[0], data);//прогоним обучающую выборку через сеть
getResult(neuronsInLayers[numLayers - 1], errors);//получаем выходные данные после обучающей выборки
В следующем цикле вычисляем ошибки нейронов выходного слоя:
for (uint16_t n = 0; n < neuronsInLayers[numLayers - 1]; n++) {
neurons[n][2][numLayers - 1] = (ans[n] - neurons[n][1][numLayers - 1]) * (neurons[n][1][numLayers - 1]) * (1 - neurons[n][1][numLayers - 1]);
}Следующим шагом начинаем идти от последнего слоя к первому, рассчитывая ошибку каждого нейрона и корректировку связи:
for (uint8_t L = numLayers - 2; L > 0; L--) {
for (uint16_t neu = 0; neu < neuronsInLayers[L]; neu++) {
for (uint16_t lastN = 0; lastN < neuronsInLayers[L + 1]; lastN++) {
neurons[neu][2][L] += neurons[lastN][2][L + 1] * weights[neu][lastN][L] * neurons[neu][1][L] * (1 - neurons[neu][1][L]);
weights[neu][lastN][L] += neurons[neu][1][L] * neurons[lastN][2][L + 1] * acs;
}
}
}
Полностью функция выглядит так:
void NeuralNet::learnBackpropagation(double* data, double* ans, double acs, double k) { //k - количество эпох обучения acs- скорость обучения
for (uint32_t e = 0; e < k; e++) {
double* errors = new double[neuronsInLayers[numLayers - 1]];
Forward(neuronsInLayers[0], data);
getResult(neuronsInLayers[numLayers - 1], errors);
for (uint16_t n = 0; n < neuronsInLayers[numLayers - 1]; n++) {
neurons[n][2][numLayers - 1] = (ans[n] - neurons[n][1][numLayers - 1]) * (neurons[n][1][numLayers - 1]) * (1 - neurons[n][1][numLayers - 1]);
}
for (uint8_t L = numLayers - 2; L > 0; L--) {
for (uint16_t neu = 0; neu < neuronsInLayers[L]; neu++) {
for (uint16_t lastN = 0; lastN < neuronsInLayers[L + 1]; lastN++) {
neurons[neu][2][L] += neurons[lastN][2][L + 1] * weights[neu][lastN][L] * neurons[neu][1][L] * (1 - neurons[neu][1][L]);
weights[neu][lastN][L] += neurons[neu][1][L] * neurons[lastN][2][L + 1] * acs;
}
}
}
}
}
А теперь тесты
Основные моменты для работы сети мы уже прописали. Сейчас давайте накидаем демонстрационный код:
#include <stdio.h>
#include "neuro.h"
int main()
{
uint16_t neurons[3] = {16, 32, 10}; //в данном массиве содержится количество нейронов в каждом слое, кол-во нейронов на втором слое взято с потолка
/* каждый нейрон первого слоя воспринимает значение одного "пикселя" из матрицы
каждый нейрон последнего слоя обозначает одно из десятичных цифр
*/
NeuralNet net(3, neurons);
double teach[4 * 4] = {// создаём "рисунок" цифры "4" для обучения, кол-во пикселей: 4*4 = 16
1,0,1,0,
1,1,1,0,
0,0,1,0,
0,0,1,0,
};
double test[4 * 4] = {//рисуем цифру "4", но по-другому
1,0,0,1,
1,1,1,1,
0,0,0,1,
0,0,0,1,
};
double ans[10] = {0, 0, 0, 0, 1, 0, 0, 0, 0, 0,};// тут мы содержим ответы для обучающей выборки, "1" на пятом месте означает, что в тестовой выборке содержится цифра "4"
double output[10] = { 0 };// массив для выгрузки данных из сети
net.Forward(4*4, teach); // проверяем работу необученной сети
net.getResult(10, output);
for (uint8_t i = 0; i < 10; i++) printf("%d: %f \n", i, output[i]*100); //выводим результат работы
net.learnBackpropagation(teach, ans, 0.50, 1000); //обучаем сеть на выборке "test", скорость обучения: 0.5
printf("\n");
net.Forward(4 * 4, test);// проверяем работу сети после обучения
net.getResult(10, output);
for (uint8_t i = 0; i < 10; i++) printf("%d: %f \n", i, output[i]*100);
return 0;
}
Получаем в выводе следующую картину:

В первом столбике представлена вероятность (в процентах), нахождения в обучающей выборке конкретной цифры до обучения, от 0 до 9. А распределение вероятности после обучения представлено во втором столбике. Вот мы и видим, что в тестовой выборке наиболее вероятно находится цифра «4»
Дабы быть честным, скажу что мы, по-большому счёту, не обучили сеть. Одной обучающей выборки ничтожно мало для полноценного использования сети. Эта проверка больше нужна для проверки работы алгоритма. Итак, нужно достаточно большое число выборок, чтоб обучить сеть качественно.
В конце хотелось бы сказать...
А на этой ноте изучение персептрона мы завершим. Далее можно заниматься оптимизацией кода, некоторые пути улучшения были описаны в прошлых частях.
Спасибо за уделённое статье внимание, и за комментарии к предыдущей публикации. Продублирую ссылку на файлы библиотеки.
Оставляйте свои комментарии, предложения. До скорого!

