Введение

Самая известная криптографическая проблема - передача секретных сообщений. Для этой задачи чаще всего используют криптосистемы с закрытым ключом: Алиса (отправитель) шифрует информацию с помощью ключа, а Боб (получатель) им же расшифровывает сообщение. К сожалению, криптосистемы с закрытым ключом имеют серьезные сложности в практической реализации. Основная вопрос - как раздать ключи? Во многих отношениях распределение ключей так же трудоемко, как и основная задача приватного общения. Злонамеренная третья сторона может подслушать ключ и легко прочитать сообщение.

Чтобы этого избежать, придумано множество способов, в этой статье мы рассмотрим квантовый, в котором секретность ключа гарантирована законами квантовой механики. Первая схема квантового распределения ключей (КРК) BB84 была разработана в 1984 году физиками Чарльзом Беннеттом и Жилем Брассаром. Ее основная идея состоит в том, чтобы использовать квантово- механический принцип (принцип неопределенности), согласно которому наблюдение в целом нарушает наблюдаемую систему. Таким образом, перехватчик, который подслушивает Алису и Боба, "портит" сообщение. Тогда его можно легко вычислить и выбросить "плохие" биты, а если их слишком много - начать все заново.

Азы квантовой механики

Не будем вдаваться в подробности, а просто сформулируем основные утверждения. Начнем с принципа неопределенности. Он гласит, что некоторые физические величины вместе абсолютно точно не измеряются. Приведем в пример импульс и координату частицы: если поместить частицу в прибор точно измеряющий координату (например он показал ),а потом в прибор точно измеряющий импульс, то второй прибор выдаст случайное число(пусть это число , т.е.). Важный момент: раньше это была частица с координатой , теперь это частица с импульсом . Если ее поместить обратно в прибор измеряющий координату, он выдаст случайное число.

Теперь перейдем к поляризациям (нам неважно знать что это такое, будем считать ее просто физической величиной, характеризующей частицу). У одной поляризации есть два взаимно перпендикулярных направления, и зная какая поляризацию, мы можем эти направления определить. Пусть у нас есть две поляризации и (значками показано направление поляризации),у каждой соответственно по 2 состояния. Принцип неопределенности гласит, что не существует прибора, который смог бы различить все 4 состояния. Есть только два отдельных прибора, один различает состояния , второй . На этом факте и основан протокол BB84.

Протокол BB84

Выпишем наш словарь:

1) (индексом обозначен базис квантового состояния)

2)

3)

4)

Алиса - передает; Боб - принимает; Ева - перехватывает

На рисунке 1 показана схема передачи.

После сеанса передачи Алиса и Боб созваниваются по открытому каналу. Далее Боб спрашивает у Алисы по каждому переданному биту правильно ли он выбрал базис (сам бит не называет). Если выбранные Бобом и Алисой базисы совпадают, то бит успешно передан, если нет, то отбрасывается. В процессе передачи данных, бит мог "испортится" (при применении верной поляризации получается неправильный бит). Это может произойти например из-за активной атаки Евы или же из-за особенностей квантового канала. При просмотре бита неверной поляризацией, его поляризация изменяется и невозможно вычислить его изначальное состояние. Для проверки количества ошибок Алиса и Боб раскрывают часть неверных битов. В протоколе BB84 критической величиной ошибок является 11% [10], это значит что Ева пыталась перехватить сообщение. В таком случае перепроверяют квантовый канал и начинают заново.

Рассмотрим возможные действия Евы. Она может пытаться перехватывать биты через квантовый канал: так же как Боб случайно выбирать поляризацию. Однако ей это не сильно поможет прочитать сообщение, она, в отличие от Боба, не может переговариваться с Алисой для выбора нужных позиций битов(вероятность, того что она будет выбирать ту же поляризацию, что и Боб крайне мала для длинных последовательностей). При, этом в случае неправильно угаданных поляризаций, она будет "портить" биты. Боб и Алиса будут знать: их сообщения пытаются перехватить. Теперь пусть Ева дополнительно активно атакует классический канал (активно, то есть не просто подслушивает, а еще может менять информацию). Тогда она может представиться Алисе Бобом, прочитать сообщение, а после стать Алисой для Боба и передать сообщение дальше. В таком случае Ева прочитает секретное сообщение, а Алиса и Боб ничего не заподозрят.

Из рассмотренного выше следует, что для надежности передачи информации нужно предъявить определенные требования к каналам связи:

1)Информацию из квантового канала можно менять, но нельзя подслушать.

2)Информацию из классического канала можно прослушивать, но ни в коем случае нельзя менять.

КРК основанное на ЭПР

Данный протокол напоминает BB84, однако обладает некоторыми преимуществами, связанными с использованием Парадокса Эйнштейна-Подольского -Розена. Напомним в чем его суть. Пусть у нас есть две одинаковые частицы A и B, которые образовались в результате распада частицы C. Из закона сохранения импульса: . Измерим тогда у частицы A импульс, у частицы B координату, у частицы C импульс. Получается, что мы можем для частицы B измерить одновременно и координату, и импульс, а это противоречит рассмотренному выше принципу неопределенности. Если законы квантовой механики не нарушаются, то измерение импульса частицы A равносильно измерению импульса частицы B. Таким образом первая частица мгновенно действует на вторую. Назовем такие частицы ЭПР парой (еще их могут называть запутанными частицами)и перейдем непосредственно к протоколу.

После этого Алиса и Боб созваниваются по открытому каналу и смотрят, какие поляризации у них совпали, а потом конвертирует их в последовательность 0 и 1.

Объясним в чем отличие этих двух протоколов. В BB84 состояния передаются по квантовому каналу от Алисы к Бобу. В BB84 ключ полностью защищен только при создании, а после его приходится хранить классическим образом. В ЭПР Алиса может отправить вторую запутанную частицу Бобу, а потом они их могут хранить до непосредственного использования ключа в квантово защищенном режиме.

Криптоанализ и безопасность КРК

Рассмотрим более подробно защищенность квантового распределения ключей.

Теорема 1 Если

1) квантовая механика верна

2) аутентификация безопасна

3) устройства достаточно безопасны,

то с большой вероятностью ключ, установленный квантовым распределением ключей, является случайным секретным ключом независящим от входных значений.

Предположение 1 Квантовая механика верна. Это предположение требует, чтобы любой перехватчик был ограничен законами квантовой механики. В частности, мы позволяем перехватчику технологию квантовых вычислений, гораздо мощнее нынешнего.

Предположение 2 Аутентификация безопасна. Это предположение является одной из самых проблемных в квантовой криптографии. Это предположение необходимо для защиты от атаки злоумышленника на классический канал связи.

Предположение 3 Устройства безопасны. Создание надежной реализации КРК - серьезная инженерная задача, над которой исследователи все еще работают. Доказательства безопасности, направлены на минимизацию предположений о безопасности физических устройств. Кажется разумным ожидать, что дальнейшие теоретические и инженерные достижения в конечном итоге принесут устройства, в чьей безопасности можно быть уверенным.

Проиллюстрируем важность третьего предположения. Скрытое устройство связи может быть спрятано внутри оборудования, рассмотрим, как пример, оптоволоконные модуляторы фазы ниобата лития, использующиеся во многих схемах КРК. Модуляторы ниобата лития поставляются с завода в герметичной коробке. Эта запечатанная коробка a) имеет полную информацию о значениях битов в настройке Алисы (базисы, несущие напряжение модуляции, значения битов подаются непосредственно на его разъемы); б) имеет доступ к оптоволоконному каналу; в) имеет значительную электрическую мощность г) не может быть вскрыт для проверки без нанесения вреда устройству. Это позволяет скрыть "жучок" внутри нормально функционирующего фазового модулятора, который будет сообщать бит значения через оптоволоконный канал и управляться через оптоволоконный канал.

Безопасность протокола BB84 для идеального случая доказана Майерсом [7], а так же многими другими. Для идеальной модели количество битов окончательного секретного ключа на бит просеянного ключа. Выражается формулой [8]

Где H двоичная Шенноновская энтропия, а QBER количество ошибок измеренных Бобом.

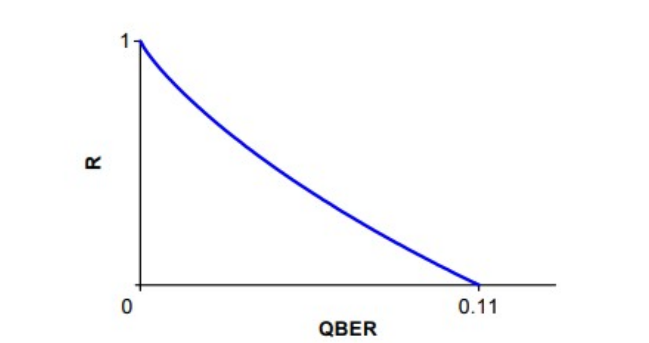
Перейдем теперь к реальной жизни, где для злоумышленника открываются обширные возможности для атак. Начнем с источника фотонов. В идеале он должен выдавать их по одному, такие устройства существуют, однако стоят больших денег. Поэтому производители используют обычные лазеры на аттенюаторе (прибор, который уменьшает амплитуду, без существенного искажения сигнала). Проблема в том, что такие лазеры с довольно большой вероятностью дают на выходе в одном световом пакете больше одного фотона. Это дает возможность совершить PNS атаку(photon number splitting)[2]. Ева разделяет световой пакет: один фотон пропускает, остальные хранит у себя в памяти, а все пакеты состоящие из одного фотона блокирует. Потом, после озвучивания базиса по открытому каналу, она узнает все биты ключа. Первый способ избежать таких атак, свести уровень мультифотонных пакетов к минимуму, второй включать в последовательность световых импульсов мощный эталонный импульс[1].

В 2003 году появилось два решения этой проблемы, требующих минимальных изменений протокола BB84. Первое, это протокол SARG04, основанный на BB84, но отличающийся способом детектирования ошибок. Второй - протокол с состояниями-ловушками, которые гарантированно позволяют обнаружить Еву[4]. Рассмотрим поподробнее оригинальный протокол, приведенный Хвангом в [4]. Алиса отправляет отправляет вместе с фотонами, отвечающими за ключ, фотоны-ловушки. После передачи она сообщает Бобу какие биты были ловушками, а какие ключами. После этого Боб измеряет пропускную способность канала для состояний-ловушек и состояний несущих информацию. если они сильно различаются, значит была проведена PNS атака. На основе этой идеи возник протокол Lo05[5]. Хой-Квонг Ло и др. придумали как можно реализовать шифрование с фотонными ловушками на уже существующем оборудовании (добавили состояния-ловушки в GLLP[3]) и провели подробный криптографический анализ, так как Хванг ограничился лишь эвристическими рассуждениями. Их результаты значительно увеличили надежность квантового распределения ключей и расстояние ,на которую передается ключ по сравнению с более ранними методами (см рис.3).

Теперь рассмотрим протокол SARG04[1]. Алиса случайно отправляет одно из четырех состояний: . В данном случае закодированным битом является БАЗИС состояния (ЭТО КРАЙНЕ ВАЖНО!!!). Боб, так же как и в BB84, их принимает. Дальше, на шаге сравнения базисов, Алиса публично объявляет одну из четырех пар неортогональных состояний:

.

Пусть для определенности Алиса отправила и объявила пару (одно состояние в паре обязательно отправленное состояние, а второе случайное из другого базиса). Если Боб мерил в базисе , он может получить точный результат, однако этот результат равновероятен для обоих базисов из пары(так как правильный результат одинаков для обоих базисов). Ему придется отбросить это значение. Если он взял базис (в этом случае равновероятно получится или )и получил , он опять не может их различить( по той же самой причине). Однако если он измерил в базисе и получил (вероятность этого 1/4), он понимает, что отправленное состояние (в правильном базисе обязательно получилось бы , а он получил , значит неверный базис). Данная модификация сильно усложняет Еве проведение PNS атаки: ей нужно блокировать все импульсы, содержащие 1 или 2 фотона, и разделять где 3 и больше. Более подробный анализ протокола можно посмотреть в [1].

Однако все не так просто, как может показаться. SARG04 уязвим для LPA(large pulse attack). Пусть Ева запустит яркую вспышку света в линию передачи, тогда часть света попадет в передающее устройство и отразится от некоторых оптических приборов внутри него(любой реальный объект имеет ненулевой коэффициент отражения). Таким образом импульс света может попасть во внутренний модулятор и промодулироваться им. Измеряя промодулированный импульс, Ева получит некоторую информацию о настройках модулятора [6].

Кроме пассивного прослушивания, Ева может действовать более активно. Например, изменять параметры настройки установок Алисы и Боба. Коротко обсудим некоторые возможные вредоносные изменения. Для примера возьмем установку одной из двух современных коммерческих схем КРК, продаваемой id Quantique [9], показанной на рис.4

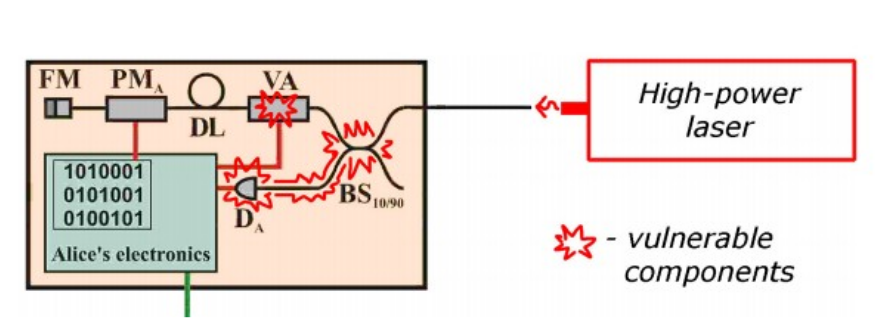
Детектор DA, кроме детектирования сигналов Боба, автоматически отслеживает сильную импульсную атаку и ее нейтрализует или бьет тревогу, в зависимости от настроек. Детектор также генерирует сигнал запуска, используемый для синхронизации часов Алисы и Боба. Если чувствительность к падающему свету значительно снизится, или если ослабление регулируемого аттенюатора значительно уменьшится по сравнению с заводской калибровкой, схема становится небезопасной. В таком случае Ева сможет провести импульсную атаку (среднее количество фотонов в световом пакете увеличивается). Для достижения этой цели Ева может: 1) попытаться сжечь детектор; 2) повредить разъемы в детекторе, чтобы уменьшить ослабление аттенюатора; 3)повредить светоделитель BS (надеясь, что его коэффициент расщепления изменится в лучшую для нее сторону); Ева может попытаться контролировать место и характер повреждения, варьируя такие параметры, как длина волны, поляризация, энергия и временной профиль своего лазерного импульса.

Напоследок кратко обсудим атаку с перехватом и повторной передачей, при которой Ева не пытается восстановить исходные состояния, а сохраняет импульсы Алисы себе и пересылает их копии Бобу. В этом случае Алиса и Боб даже не будут подозревать о взломе. Такие световые импульсы называются ложными состояниями. Поддельные состояния специфичны для каждой конкретной схемы или даже конкретного образца атакуемого оборудования. Успешная атака с использованием фальшивых состояний дает Еве полное знание ключа.

Заключение

Может возникнуть закономерный вопрос, неужели нельзя передавать ключи более простым образом? Ведь квантовая криптография дорогое удовольствие: нужен оптоволоконный квантовый канал, фотонная пушка, которая могла бы выстреливать по одному фотону, приборы для определения состояния. К тому же до 1984 года люди как-то справлялись с шифрованием данных, зачем все менять? Дело в том, что классическая криптография базируется на сложности математических задач, например дискретном логарифмировании (RSA). Эти задачи обычные компьютеры решают очень долго, однако в 1994 году Питер Шор предложил алгоритмы их решения на квантовом компьютере. Поэтому требуется создавать новые методы шифрования и перераспределения ключей, невзламываемых любыми вычислительными мощностями. Как можно было заметить неприступная на бумаге квантовая криптосистема на деле дает сбои, так что криптоаналитикам предстоит еще много работы, чтобы сделать эти системы полностью безопасными.

Источники:

1) A. Acin, N. Gisin, and V. Scarani, “Coherent-pulse implementations of quantum cryptography protocols resistant to photon-number-splitting attacks”

2) C. Bennett, F. Bessette, G. Brassard, L. Salvail, and J. Smolin, “Experimental quantum cryptography”(1992)

3) D. Gottesman, H.-K. Lo, N. L ?utkenhaus, and J. Preskill, Quant. Inf. Comp. 4, 325 (2004)

4) W.-Y. Hwang, “Quantum key distribution with high loss: toward global secure communication”

5) Lo H., Ma X., Chen K. , “Decoy state quantum key distribution”, (2005)

6) Vadim Makarov, “Quantum cryptography and quantum cryptanalysis ”, (2006)

7) D. Mayers, “Quantum key distribution and string oblivious transfer in noisy channels” (1996); D. Mayers, “Unconditional security in quantum cryptography” (2001).

8) P. Shor and J. Preskill, “Simple proof of security of the BB84 quantum key distribution protocol”(2000).

9) D. Stucki, N. Gisin, O. Guinnard, G. Ribordy, and H. Zbinden, “Quantum key distribution over 67 km with a plug&play system”

10) Xiaoqing Tan, “Introduction to Quantum cryptography”,(2013)