История

Алгоритм TDES (3DES, Tripple DES) был создан в 1978 году как улучшение алгоритма DES. По сравнению с последним улучшилась криптостойкость, но в три раза увеличилось время вычисления. Несмотря на то, что на сегодняшний день наиболее распространен алгоритм AES, который принят в качестве стандарта шифрования правительством США, алгоритм TDES широко используется. Например, даже сейчас его можно встретить в системных продуктах компании Microsoft.

Так же алгоритм используется для потокового шифрования данных в каналах передачи, где высокая криптографическая устойчивость не нужна. Аппаратная реализация алгоритма TDES, и тем более DES, занимает меньшую площадь по сравнению с более безопасным AES, что может играть ключевую роль при выборе алгоритма. По этой причине даже сегодня его можно встретить в отечественных и зарубежных сигнальных процессорах.

Зачем я решил это сделать и описать

Действительно, эти алгоритмы уже очень глубоко исследован и не раз был описан и написан. Однако, когда я знакомился с этой темой и первый раз ради опыта решил реализовать этот алгоритм, я столкнулся с тремя проблемами. Во-первых, его аппаратная реализация ни разу не описывалась в русскоязычном пространстве, так что я решил заполнить этот пробел своей статьей. Во-вторых, большинство англоязычных статей на эту тему написаны для реализации на ПЛИС с использованием строенных ROM блоков памяти, а меня интересовала именно реализация "для кремния". И в-третьих большинство авторов приводят только часть исходного кода, но целиком исходников не так много. При этом написание этого модуля не является сложной логической задачей, но нужно безошибочно перенести все таблицы и преобразования в код. Так что отлавливать ошибки довольно рутинная и долгая задача.

Так же интересной задачей является написание тестовых векторов, которые при небольшом количестве смогли бы покрыть большую часть блока. Тестовые векторы для DES найти можно, например в [1], а вот для TDES-EDE3 мне найти ничего не удалось.

Описание алгоритма DES

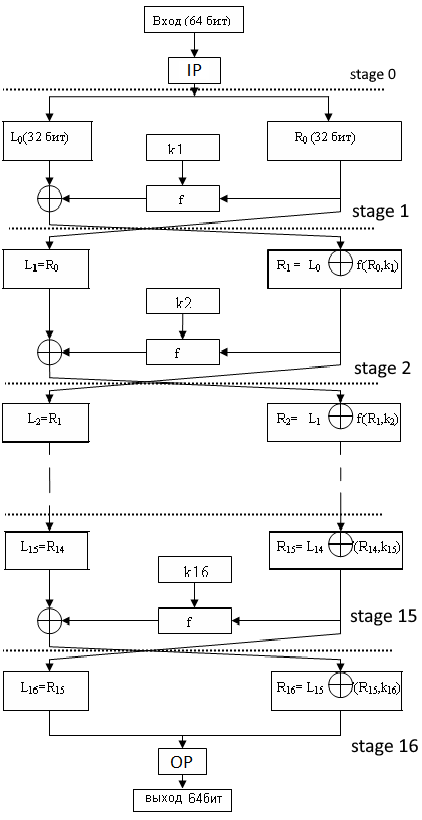
Начать знакомство с алгоритмом TDES необходимо с алгоритма DES. Приведу его краткое описание с нужными мне обозначениями.

DES является симметричным блочным алгоритмом с блоком размером 64 бит и ключом длинной 56 бит (либо расширенным ключом длинной 64 бит). Все таблицы преобразований и перестановок в удобном виде находятся в excel файле на моем гитхабе. Алгоритм шифрования представлен на рисунке 1 и состоит из следующих этапов:

• Начальная перестановка IP. На этом этапе исходный блок размера 64 бит преобразуется в блок T такого же размера при помощи перестановки IP.

• 16 раундов шифрования. Входной блок T₀ разбивается на старшую часть L₀ и R₀. Далее вычисления задаются рекуррентным соотношением:

  

• Генерирование ключей k_i. В первую очередь исходный ключ расширяется добавлением бит в позиции 8, 16, 24, 32, 40, 48, 56, 64 таким образом, чтобы каждый байт содержал нечетное число единиц. Хотя на практике обычно все устроено наоборот. На вход подается уже расширенный 64-битный ключ, из которого потом выбираются значимые 56 бит. Это используется для обнаружения ошибок при передаче ключей, если такое необходимо. Далее, производится перестановка KI согласно таблице (она записана для 64-битного ключа), причем добавленные биты в перестановке не участвуют. Полученный блок делится на старшую и младшую части размером 28 бит. Для получения следующего ключа используется циклическая перестановка влево значений внутри каждой части на величину, зависящую от номера раунда: для первого, второго, девятого и шестнадцатого раундов происходит перестановка на два, для всех остальных на один.

  Сам же ключ имеет длину 48 бит и выбирается из 56 битного вектора согласно преобразования KO.

• Вычисление функции f. Аргументами функции f являются 32-битовый вектор R_(i-1) и 48-битный ключ k_i. Для вычисления функции f последовательно используются:

  • Функция расширения E. Расширяет 32-битовый вектор R_(i-1) до 48 бит согласно таблице преобразования E.

  • Xor с ключом.

  • Преобразование S. Полученный вектор делится на 8 блоков по 6 бит каждый. Каждый из восьми блоков преобразуется согласно S-таблицам. Пара старший и младший бит из блока определяют столбец, остальные четыре бита определяют строку.

  • Перестановка P. Производится перестановка согласно таблице P. В результате получается вектор длинной 32 бита.

• Конечная перестановка OP. После 16 раундов шифрования производится конечная перестановка согласно таблице OP.

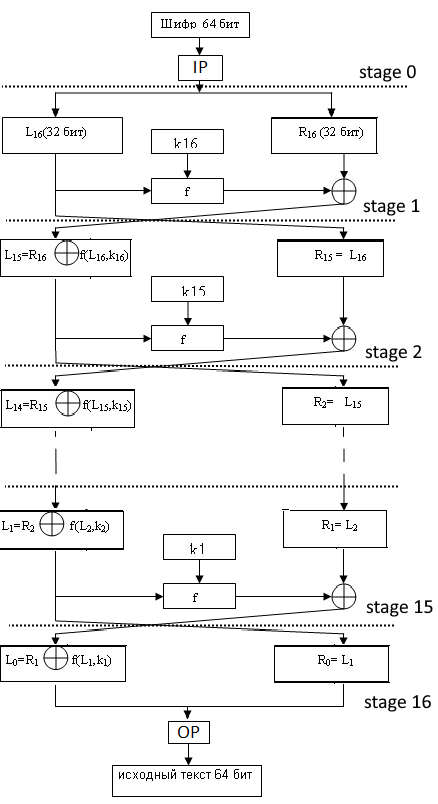
Расшифровка DES проводится в обратном порядке (рис. 2). В раундах используется обратное преобразование сетью Фейстеля.

Аппаратная реализация DES

Для написания быстрой аппаратной реализации буду использовать конвейер. За основу брал работу [2], однако генерирование ключа решил делать по-другому. Стоит обсудить стадии вычислений.

Начальная перестановка не требует никаких логических элементов, так что эта стадия однозначно быстрая, то же касается конечной перестановки и всех перестановок в генерировании ключа. Вычисление ключей делается параллельно с самим шифрованием, единственная стадия вычислений, требующая времени, это расширение исходного ключа битами для обнаружения ошибок. Хотя, как я писал выше, зачастую ключ приходит уже расширенный, так что эта часть вычислений оказывается ненужной.

Самая долгая часть это раунд шифрования, а именно, вычисление функции f. Функция расширения не требует логических элементов в реализации, то же касается перестановки P. Так что потребуется время на xor с ключом, и, самое долгое, преобразование S.

Преобразование S буду реализовывать при помощи таблицы поиска.

Теперь можно обсудить конвейеризацию. Самый очевидный и практически удобный вариант разбить на стадии по каждому раунду (см. рис. 1). Так же удобно добавить входные триггеры, на рисунке это stage 0.

Перейду к блоку, который будет производить шифрование одного раунда. Это, во-первых, вычисление функции f, а во-вторых вычисление рекуррентного соотношения для R_i. На вход блока подается два вектора R_(i-1) и L_(i-1) длинны 32 бит и ключ k_i длинны 48 бит. На выходе блока формируется результат раунда R_i и L_i. Вычисление ключа сделаю в отдельном блоке. Весь код написан на языке System Verilog.

Генерация ключа производится последовательным сдвигом на каждой стадии, таким образом следующий вектор можно загружать сразу после первого раунда шифрования.

Так же нужны сигналы загрузки и готовности результата, однако я их не реализовывал, потому что в зависимости от задачи на них ставятся различные требования, а для тестирования можно обойтись и без них, просто последовательно загружая данные.

Так же понадобится реализация функции f_decrypt. Т.к. расшифровка производится обратной сетью Фейстеля, то по сути нужно просто поменять местами L_out и R_out в блоке f_encrypt. Так же придется изменить блок генерации ключей, т.к. теперь 16-й ключ нужен на первой стадии, 15-й на второй и т.д.

Все исходники загружены на мой гитхаб.

Теперь опишу тестирование блока DES. Тестировать отдельные функции перестановки я не вижу смысла потому что для их тестирования логично подавать векторы с одним битом равным единицы и всеми остальными равными нулю, а тогда проверка результата сводится к повторению написания таблицы перестановки. Так что для их проверки выпишу несколько произвольных входных векторов и ключей.

Имеет смысл проверить S-таблицы. Для этого я выпишу 512 = 64*8 тестовых вектора с ключом такие, что они покрывают все значения в S-таблице. Я использовал все ключи key = 64'h0, а тестовые векторы генерировал таким образом: выбираю S-таблицу, выбираю в ней ячейку, которую я хочу протестировать. Выписываю вектор, в котором нужные биты для для выбранной ячейки равны единицы, а все остальные равны нулю. Далее, я делаю обратную перестановку функции расширения E и полученный 32-битный вектор дополняю нулями до 64-битного. И, наконец, делаю обратную перестановку OP. Таким образом, каждый вектор последовательно пробегает каждую ячейку S-таблицы. С получившимися тестовыми векторами можно ознакомится в файле тестбенча на гитхабе.

Для тестирования блока расшифровки я использовал те же тестовые векторы, только поменял местами входной вектор с ожидаемым результатом.

Т.к. реализация у меня конвейеризированная, то в одном параллельном блоке по каждому отрицательному фронту я выставляю значения ключа и данных, а в другом параллельном блоке сначала жду 17 положительных фронтов (16 стадий вычисления и одна входная), а затем по каждому положительному фронту читаю значение и сравниваю с ожидаемым.

Теперь, у меня есть написанный и протестированный RTL модуля DES для шифрования и дешифровки.

Аппаратная реализация алгоритма TDES

Алгоритм TDES состоит из комбинации трех стадий шифрования и расшифровки. Наиболее распространен 3DES-EDE3 (encrypt-decrypt-encrypt) с тремя разными ключами. Таким образом, длина ключа 168 бит (расширенный 192 бит), размер блока все так же равен 64 бит.

Для реализации этого алгоритма нужно соединить блоки шифрования и расшифровки. При этом нужно добавить дополнительную цепочку триггеров для задержки ключа до следующих блоков на время исполнения 16 раундов. При таком соединении блоков будут последовательно происходить перестановки IP и OP, которые являются обратными. Однако при последующем синтезе эти перестановки будут оптимизированы и заменены прямыми соединениями. RTL блока находится в приложении.

Тестовые векторы строил следующим образом: взял тестовые векторы для DES шифратора, ключ из этих векторов есть ключ первой стадии TDES. Ключи второй и третьей стадии одинаковые и равны 64'hffffffffffffffff. Таким образом, я проверяю S-блоки первого шифрования TDES, т.к. далее идет расшифровка и шифрование с одинаковым ключом, то ожидаемый результат совпадает с результатом после первой стадии, а он же результат из тестов на DES. Таким же образом тестирую последнее шифрование TDES. Если сейчас все хорошо, то я считаю, что две части из трех работают правильно, а тогда я могу проверить S-блоки стадии расшифровки с теми же входными и ожидаемыми векторами, что и в DES и ключами равными 64'h0.

Таким образом получается 512*3 = 1536 тестовых вектора. Тестовые векторы для TDES находятся в файле тестбенча на гитхабе.

Итог

Я написал и протестировал RTL алгоритмов шифрования DES и TDES-EDE3. Так же я написал тестовые векторы для этих алгоритмов. Все исходники на гитхабе, надеюсь они помогут Вам в знакомстве или даже реализации этих алгоритмов. Спасибо за внимание!

Полезные ссылки:

• [1]

• [2]

• Хорошая статья с примерами вычислений по стадиям

• Гитхаб с исходниками