12.12.2020 12:20
analog_design 19 5900 Источник
Микроэлектромеханические системы (МЭМС) — устройства, объединяющие в себе микроэлектронные и микромеханические компоненты. Сейчас довольно трудно встретить системы в которых не используются датчики, выполненные по данной технологии. Но как устроены современные датчики и какие преобразователи используются для работы с ними? Постараемся детально разобраться в этом вопросе, основываясь на работе современных МЭМС-акселерометров.


Простейший акселерометр, как он работает?


Акселерометр — прибор, измеряющий проекцию кажущегося ускорения (разности между истинным ускорением объекта и гравитационным ускорением). Принцип работы можно объяснить с помощью простой модели.


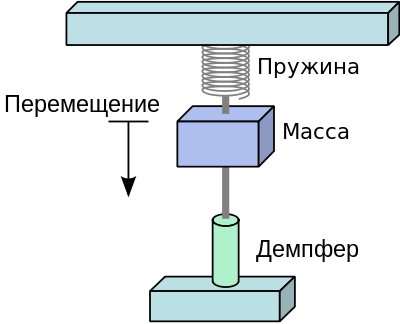
Модель устройства механического акселерометра (оригинал)

При увеличении ускорения, масса будет растягивать пружину. По закону Гука из школьной программы физики можно с легкостью найти ускорение системы:

$a=\frac{k\cdot\delta x}{m}$, где k -коэффициент упругости пружины, $\delta x$ – ее растяжение и m – масса груза.

Используя три перпендикулярно расположенных датчика, можно узнать ускорение предмета по 3-м осям, и зная начальные условия определить положение тела в пространстве.

Эта незамысловатая модель представляет собой основу работы большинства акселерометров, которые можно поделить на 3 основные подгруппы:

  • механические
  • электронные
  • пьезоэлектрические

Есть еще термальные и оптические, однако их рассматривать не будем. Если с механическими все понятно (по сути, их работу отражает модель сверху), то с электронными и пьезоэлектрическими немного поинтереснее.

Пьезоэлектрический акселерометр


Основывается данный тип датчиков на пьезорезистивном эффекте, который был открыт в 1954 году Смитом в таких полупроводниках как германий и кремний. В отличие от пьезоэлектрического эффекта, пьезорезистивный эффект вызывает изменение только электрического сопротивления, но не электрического потенциала.


Анимация пьезоэффекта (оригинал)

При увеличении ускорения, инертная масса увеличивает/уменьшает давление на пьезоэлемент. Благодаря пьезоэффекту происходит генерация сигнала, который зависит от внешнего ускорения.


Устройство пьезоэлектрического акселерометра (оригинал)

Датчики такого типа требуют дополнительного усилителя, который увеличивает амплитуду сигнала, и создает низкоимпедансный выход для работы с внешними устройствами. Для калибровки нулевого значения ускорения используется Preload Bolt, масса которого рассчитана так, чтобы соответствовать нулевой точки ускорения в системе.

Датчики такого типа до сих пор сильно распространены, и в основном применяются в системах, требующих высокую надежность — automotive. Для коммерческой электроники зачастую используют электронные акселерометры, которые имеют меньший размер и цену.

Электронные акселерометры


Принцип работы электронных датчиков основан на изменении емкости конденсаторов при изменении ускорения. Простейшая модель работы представлена на картинке.


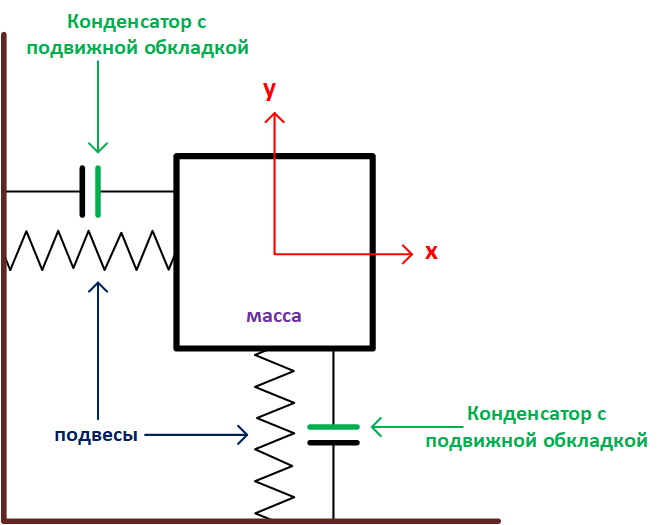
Устройство 2-х осевого электро-механического акселерометра

При изменении ускорения, масса изменяет расстояние между обкладками конденсатора. Из простейшей формулы емкости конденасатора $C=\frac{\varepsilon\varepsilon_0S}{d} $ следует, что при изменении d расстояния между обкладками емкость конденсатора будет также изменяться. Широкое применение данный метод получил, благодаря развитию МЭМС (MEMS)– микроэлектромеханических систем.

МЭМС технологии позволяют создавать конденсаторы с подвижными обкладками на кремниевой подложке, что существенно уменьшает размер устройства, и что не маловажно – его стоимость.


Устройство 2-х осевого электро-механического акселерометра (оригинал из книги «Introductory MEMS». Дальнейшие иллюстрации тоже взяты из этой книги)

У читателя наверняка возник вопрос: “как именно детектировать изменение емкости конденсатора?” Постараюсь дать на этот вопрос исчерпывающий ответ.

Устройство МЭМС акселерометра. Как превратить изменение емкости в сигнал?


Емкостной полумост


Итак прежде, чем описывать работу самого датчика, обратимся к довольно популярной схеме в схемотехнике – емкостному полумосту (Capacitive half-bridge).

Емкостной полумост — основа МЭМС-датчиков

Напряжения $e_1$ и $e_2$ являются входными, а $e_3$ – выходной сигнал для последующего преобразования. Емкости обоих конденсаторов зависят от внешнего ускорения, и изменяются на величину x(t). При x = 0, заряды на емкостях являются идентичными, и при этом $C_1=C_2=C_0$. При условии, что x <<d найдем как зависит изменение емкости конденсаторов от изменения положения обкладки.

Вывод формулы для изменения емкости
Запишем изменение каждой емкости при сдвиге обкладки на x:

$\Delta C_1=C_1-C_0; \ \ \ \ \ \ \Delta C_2=-C_2+C_0 \ \ \ \ \ \ (1.1)$


Запишем через формулу емкости:

$\Delta C_1=\frac{\varepsilon S}{d-x}-\frac{\varepsilon S}{d}; \ \ \ \ \ \ \Delta C_2=-\frac{\varepsilon S}{d+x}+\frac{\varepsilon S}{d}$


Упростив данные формулы, получаем следующее:

$\Delta C_1=\frac{\varepsilon Sx}{d^2-xd}; \ \ \ \ \ \ \Delta C_2=\frac{\varepsilon Sx}{d^2+xd}$


Учитывая условие, что x <<d, а xd несущественно по сравнению с d^2 можем записать формулу изменения емкости конденсатора, в зависимости от смещения обкладки:

$\Delta C\left(x\right)=\frac{\varepsilon S}{d^2}x \ \ \ \ \ \ (1.2)$


Итак часть пути пройдена, мы получили как зависит значение изменения емкости от изменения положения обкладки (то есть внешнего ускорения). Пора это изменение детектировать: вводим дополнительные токи — $i_1, i_2, i_3$. Теперь остается вычислить как выходной ток будет зависеть от изменения положения обкладки.


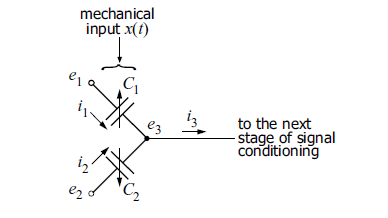
Емкостной полумост — токи

Вывод формулы зависимости выходного тока от изменения емкости
По правилу Кирхгофа для токов получаем следующее уравнение:

$i_1+i_2=i_3$


Учитывая тот факт, что ток является производной заряда dq/dt, а заряд q=CU, преобразуем данное уравнение в следующий вид:

$i_3=\frac{d}{dt}\left[C_1\left(e_1-e_3\right)\right]+\frac{d}{dt}\left[C_2\left(e_2-e_3\right)\right] \ \ \ \ \ \ (1.3)$


Пусть потенциалы $e_1= e_2= e_s$, тогда исходя из формулы (1.1):

$i_3=\frac{d}{dt}\left[\left(C_0+\Delta C\right)\left(e_s-e_3\right)\right]+\frac{d}{dt}\left[\left(C_0-\Delta C\right)\left(e_s-e_3\right)\right]$



Итак если использовать одинаковые потенциалы входных напряжений $e_1= e_2= e_s$ получаем зависимость тока:

$i_3=\frac{d}{dt}\left[2C_0\left(e_s-e_3\right)\right]$

Результат получился довольно странный: выходной ток никак не зависит от изменения емкости. Для того, чтобы детектировать изменение емкости, необходимо задавать на обкладках напряжения разной полярности, то есть: $e_1=e_s$, а $e_2=-e_s$. Тогда переделаем уравнение с учетом данной модификации.

Зависимость тока от изменения положения обкладки с учетом разной полярности входных напряжений
Перепишем уравнение 1.3:

$i_3=\frac{d}{dt}\left[\left(C_0+\Delta C\right)\left(e_s-e_3\right)\right]+\frac{d}{dt}\left[\left(C_0-\Delta C\right)\left(-e_s-e_3\right)\right]$


Упрощаем:

$i_3=2\frac{d}{dt}\left(\Delta C e_s-C_0e_3\right)$


Берем производную:

$i_3=2\left(e_s\frac{d}{dt}\left(\Delta C\right)+\Delta C\frac{d}{dt}\left(e_s\right)-C_0\frac{d}{dt}\left(e_3\right)\right)$


Учитывая уравнение 1.2 для изменения емкости, получаем:

$i_3=2\left(e_s\frac{\varepsilon S}{d^2}\dot{x}+x\frac{\varepsilon S}{d^2}\dot{e_s}-C_0\dot{e_3}\right) \ \ \ \ \ (1.4)$


Из этого уравнения видны следующие факты:
  • если положение пластин не меняется во времени, то $\dot{x}=0$
  • аналогично если источник сигнала $e_s$ постоянный (DC), то $\dot{e_s}=0$

Для эффективной работы емкостного полумоста необходимо использовать переменные входные сигналы e1 и e2, смещение фаз между которыми будет равно 180 градусов (для того, чтобы потенциалы имели разный знак). Поэтому получаем следующий вид сигналов:

$e_1=+e_s=+Bsin\left(\omega t\right)$

$e_2=-e_s=-Bsin\left(\omega t\right)$

, где $\omega$ – частота переменного сигнала (определяется на этапе разработки, в зависимости от полосы пропускания системы и нормальной работы механических емкостей).

Итак, мы получили уравнение (1.4), которое показывает, как изменение емкости конденсатора влияет на выходной сигнал системы. Однако такой сигнал будет довольно малый по амплитуде, к тому же если подключим к нему нагрузку для общения с внешним миром — вся система рухнет. Тут нужен усилитель…

Просто добавь усилитель


Добавим в нашу систему усилитель (будем считать, что коэффициент усиления — $\infty$ — сл-но работает принцип виртуальной земли).


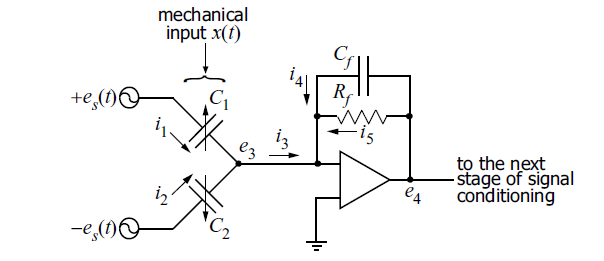
Емкостной полумост + интегратор

Итак теперь найдем зависимость выходного напряжения усилителя от изменения емкости.

Выходное напряжение усилителя
Запишем уравнение Кирхгофа для этой системы:

$i_4+i_5=i_3$


Ток через конденсатор $C_f$ можно записать через изменение заряда dq/dt, поэтому исходя из полученного уравнения (1.4) получаем:

$2\left(e_s\frac{\varepsilon S}{d^2}\dot{x}+x\frac{\varepsilon S}{d^2}\dot{e_s}-C_0\dot{e_3}\right)=\frac{d}{dt}\left[C_f\left(e_4-e_3\right)\right]+\frac{e_4-e_3}{R_f} \ \ \ \ \ (1.5)$


Данное уравнение показывает, что выходной сигнал зависит не только от положения обкладки x, но и от ее скорости движения (что не желательно). Для того чтобы компонента, вносимая скоростью, была незначительной, необходимо использовать высокочастотный входной сигнал (обычно такую частоту выбирают в районе 1 ГГц). Запишем компоненты уравнения как гармонические сигналы:

$e_s\dot{x}+x\dot{e_s}=\dot{x}Bsin{\omega t}+x\omega Bcos{\omega t}$


Выбираем частоту достаточно высокую, чтобы $ x\omega\gg\dot{x}$:

$2\frac{\varepsilon S}{d^2}x\dot{e_s}=C_f\dot{e_4}$


Учитывая, что сигналы $e_s$ и $e_4$ имеют одинаковую частоту переходим к отношению их амплитуд:

$\mid\frac{e_4}{e_s}\mid=\frac{2\varepsilon S}{C_fd^2}x$


В итоге мы получили зависимость выходного сигнала усилителя от изменения положения обкладки конденсатора. Внимательный читатель должен сразу обратить внимание – это же амплитудная модуляция! Действительно, в данной системе мы имеем сигнал x(t), который перемножается с сигналом $e_s(t)$ и усиливается на величину $\frac{2\varepsilon S}{C_fd^2}$. Следующий шаг – убрать несущую частоту $e_s(t)$, и мы получим усиленный сигнал x(t) – который пропорционален ускорению. Долгий путь вычислений привел нас к пониманию архитектуры МЭМС-акселерометра.

Архитектура МЭМС акселерометра


Рассмотрим сначала функциональную схему датчика:


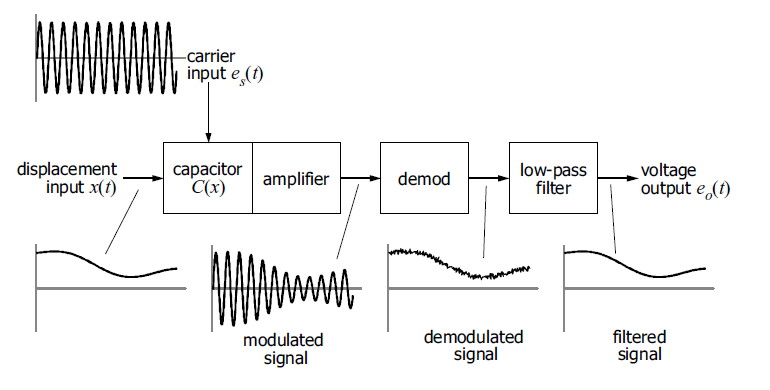
Функциональная схема МЭМС-акселерометра

Изначально у нас есть сигнал x(t) – который отражает изменение ускорения. Далее мы перемножаем его с несущим сигналом $e_s(t)$ и усиливаем с помощью операционного усилителя (в режиме интегратора). Далее происходит демодуляция – простейшая схема – диод и RC фильтр (в реальности используют усложненную схему, синхронизируя процесс модуляции и демодуляции одной несущей частотой $e_s(t)$). После чего остатки шума фильтруются с помощью фильтра низких частот.

В качестве примера приведу один из первых МЭМС акселерометров компании Analog Devices – ADXL50:


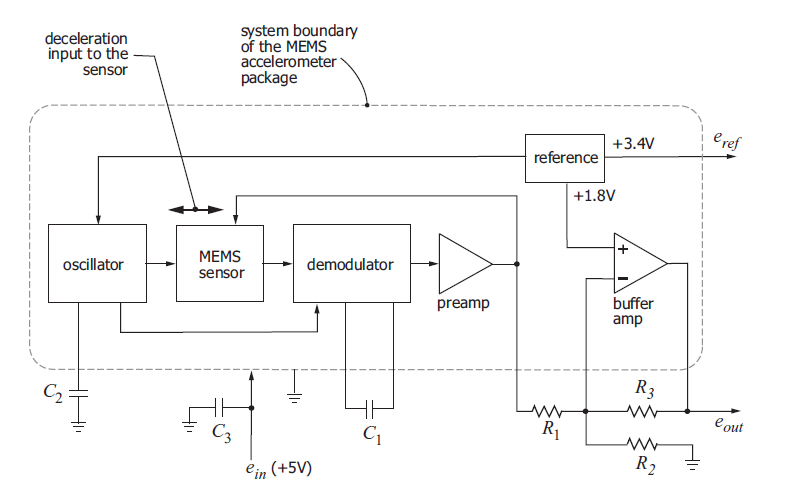
Структурная схема ADXL50

Наверное, приведя структурную схему датчика в начале статьи многим читателям не было бы понятно назначения некоторых блоков. Теперь завеса приоткрыта, и можем обсудить каждый из них:

  • Блок, который называется “MEMS sensor” – является емкостным полумостом.
  • Блок “oscillator” генерирует сигнал на частоте 1ГГц.
  • Сигнал осциллятора также используется для синхронной демодуляции.
  • Выходной усилитель и дополнительные резисторы создают нулевую точку, относительно которой можно смотреть знак изменения ускорения (обычно это VDD/2- половина питания, для биполярных датчиков — «земля»).
  • Внешняя емкость $C_1$ определяет полосу измерения системы.
  • Внутреннего фильтра низких частот в данной схеме нет, но в современных схемах они имеются.

Какой преобразователь выбрать для работы с датчиками?


Выбор преобразователя для работы с датчиками зависит от точности, которую вы хотите получить. Для работы с датчиками подойдут АЦП с архитектурой SAR или Delta-Sigma с высокой разрядностью. Однако современные датчики обладают встроенными преобразователями. Лидерами этого направления являются STMicroelectronics, Analog Devices и NXP. В качестве примера, можно привести новую микросхему с 3-х осевым акселерометром и встроенным АЦП – ADXL362.


Структурная схема ADXL362

Для работы с АЦП в схему добавлены антиэлайзинговые фильтры, чтобы исключить попадания в спектр дополнительных гармоник.

Где достать такие технологии?


Сейчас для fabless компаний доступно множество фабрик, которые предлагают технологии МЭМС. Однако для создания современных микросхем требуется интегрировать емкости с подвижными пластинами в стандартный маршрут проектирования, ведь помимо такой емкости необходимо спроектировать дополнительные блоки (генератор, демодулятор, ОУ и тд) на одном чипе. В качестве примера можно привести фабрики TSMC и XFab, которые предлагают технологию для реализации МЭМС датчика вместе со всей обвязкой. На картинке представлены емкости, которые позволяют создать трехосевой акселерометр:


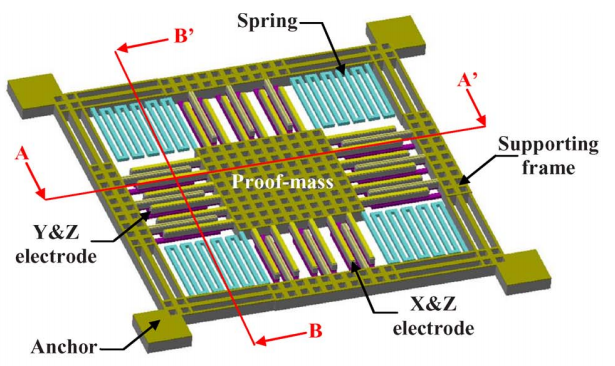
Трехосевой емкостной полумост от TSMC

В России также существует фабрика по выпуску МЭМС датчиков – “Совтест”, однако предприятие не обладает технологией интегрирования дополнительных схемотехнических блоков, которые необходимы для создания конечного устройства и единственный выход — применять технологию микросборки.


МЭМС-акселерометр разработки Совтест

Какие наработки есть у нашей компании в этом направлении?


У нас есть несколько преобразователей, которые предназначены для работы с датчиками. Из новых продуктов это:

  • 5101НВ035 – 16-канальный преобразователь на основе 8-ми Дельта-Сигма АЦП, предназначена для работы с токовыми датчиками
  • 1316НХ035 – 4-х канальный интегрирующий преобразователь напряжение-частота (ПНЧ), предназначенный для работы с 3-х осевыми акселерометрами и гироскопами.

Как я писал в предыдущей статье, период ожидания пластин с фабрики может занять довольно долгий промежуток времени. После первого тестового запуска АЦП 400МГц, время прихода пластин и дальнейших измерений заняло более полугода. За это время наша команда успела сделать ПНЧ 1316НХ035 (развитие предыдущей схемы 1316ПП1У), о котором могу немного рассказать.

Преобразователь напряжение-частота


Для преобразования данных с датчика обычно используются SAR или delta-sigma АЦП, однако существует еще один тип преобразователей — интегрирующие ПНЧ, которые имеют существенные преимущества:

  1. Занимают меньшую площадь и имеет меньшее потребление при том же показателе линейности и шума.
  2. Простая архитектура.
  3. Высокая устойчивость к входному шуму и сигналам помех.
  4. Устойчивость к шуму и помехам выходного сигнала.
  5. Возможность передачи данных без обработки на радиочастотный канал связи.

Микросхема 1316НХ035 представляет собой четырехканальный преобразователь напряжения в частоту и цифровой код, к трем основным высокоточным каналам подключаются выходы трехосевого акселерометра. 4-ый канал имеет входной 4-канальный мультиплексор, к которому можно подключать дополнительные датчики системы: температуры, влажности и др. Под микроскопом схема выглядит так:


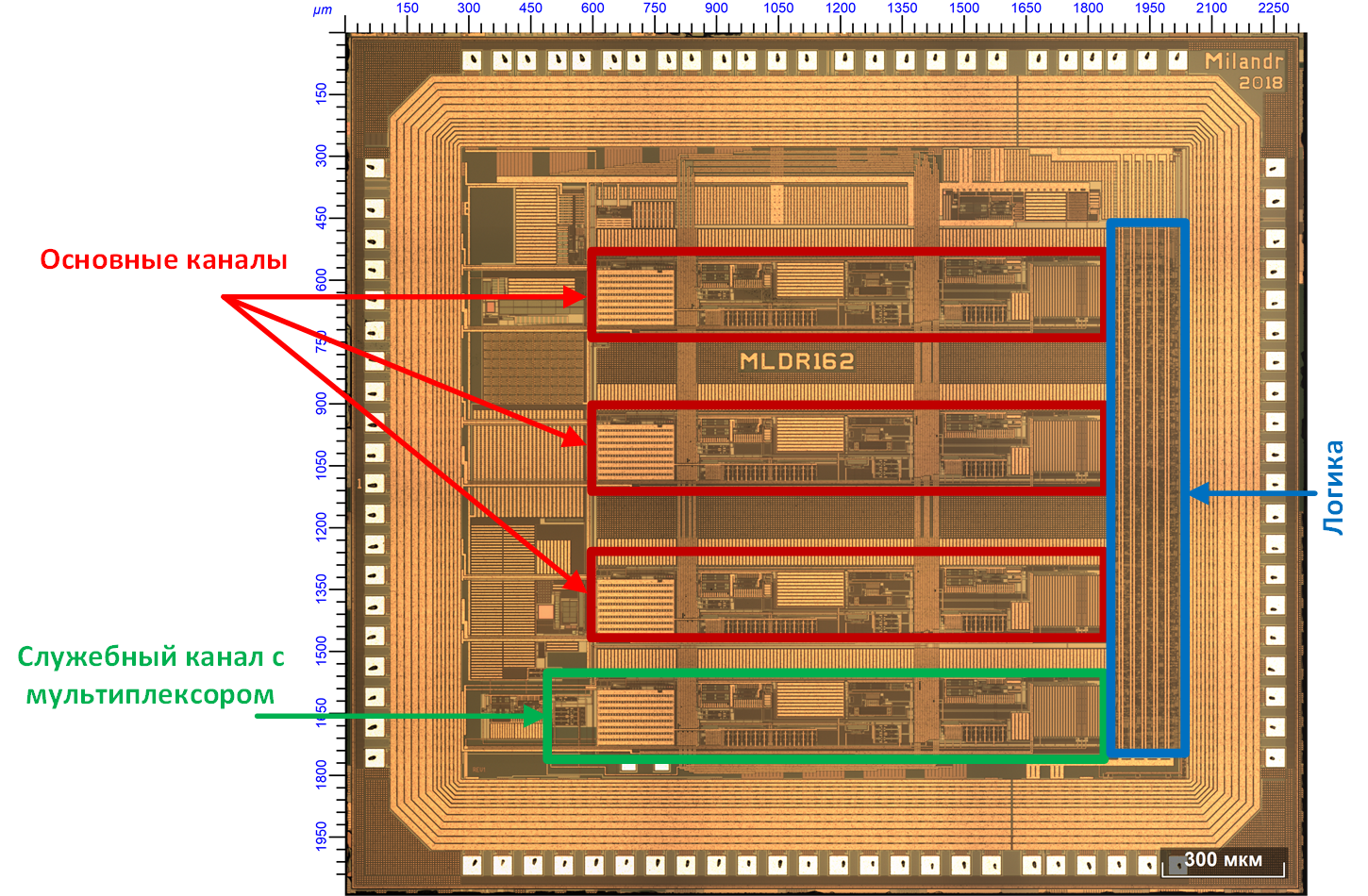
ПНЧ под микроскопом

Каждый из трех основных каналов преобразует входное напряжение в диапазоне ± 4В в частоту до 1250кГц на 3-х выходах, соответствующих положительному и отрицательному входным напряжениям. Также микросхема имеет в каждом канале 16 битный реверсивный счетчик, для подсчета частотных импульсов. SPI интерфейс служит для управления режимами преобразования и выборки содержимого счетчиков импульсов каналов. Основными требованиями к параметрам ПНЧ являлись:

  1. высокая термо и временная стабильность выходной частоты при нулевом входном сигнале (заземленных входах)
  2. динамический диапазон преобразования – не менее 22 бит
  3. непрерывность преобразования входного сигнала и недопустимость потери ни одного частотного импульса.

Для обеспечения требований 1 и 2 используется аналоговая автокалибровка, которая выполняется автоматически при включении схемы, а также может запускаться в любой момент по команде через SPI интерфейс. Требование 3 обеспечено и гарантируется схемотехническими решениями. Удалось достичь довольно приличных параметров точности: типовая нелинейность преобразования составила 30 ppm, а смещение нуля менее 0.1 Hz при коэффициенте преобразования 200 kHz/V. Динамический диапазон преобразования: fmax/fmin = 2*1.25МГц / 0.3Гц ? 8.33млн., что соответствует более 23 битам.

Есть только одно “но” – биполярное питание. Для обеспечения хорошей стабильности нуля (напряжение, которое соответствует ускорению 0g) необходимо использовать биполярное питание. Такое решение довольно эффективное – ведь когда 0g соответсвует “земля”, система априори будет стабильной. Также это улучшает проектирование системы. В современных датчиках в качестве нуля используют половину питания Vdd/2, однако если значение напряжения на преобразователе будет отличаться от напряжения на датчике – мы автоматически получаем смещение, которое нужно дополнительно калибровать.

Наверное, для многих потребителей биполярное напряжение немного отпугивает, и мы как разработчики это понимаем. Возможно, в дальнейшем сделаем коммерческий вариант для МЭМСов (или интегрируем датчик в ПНЧ). Пока, конечно, это всего лишь планы, но уверен они увидят свет.

P.S. Нашел бонусные фотографии с процесса исследования образцов. Вообще это, как по мне, самое интересное в процессе разработки. Тебе дают в руки твое детище с пылу жару с завода, ты подаешь на него питание и скрестив пальцы ждешь – “работает или нет?”.


P.P.S. Кому понравилась тема датчиков, в будущем коллега из центра проектирования аппаратуры хотел бы рассказать про создаваемую инерциальную систему на основе МЭМС датчиков — БИНС.