_{Паулюс Поттер. Медвежья охота. 1649 г. Государственный музей, Амстердам.}

В прошлый раз мы выяснили, как заработать на фондовом рынке. Нужно взять на себя систематический рыночный риск и заработать премию за риск. Теперь мы посмотрим, насколько успешно управляющие паевыми фондами справляются с этой задачей. В этой части вы узнаете:

• как оценить, насколько успешен портфельный управляющий (посчитать связь доходности портфеля с доходностью рынка);
• кто такая «альфа», и почему все её ищут (доход, превышающий обычную премию за систематический риск);
• какой из участвовавших в сравнении фондов российских акций показал лучший результат (личный портфель автора!);
• какой фокус позволил автору заработать «альфу» (ставка на конкретный систематический риск, который не видит наивная модель).

CAPM для оценки успеха управляющих фондами

Предположим, что вы дочитали до этого места и решили инвестировать свои средства в фондовый рынок. Есть несколько способов это сделать. Во-первых, вы можете сделать всё сами: открыть счёт у брокера, выбрать и купить конкретные акции, облигации или другие бумаги, а потом при необходимости перебалансировать свой портфель. Другой вариант — принести деньги в ПИФ — паевой инвестиционный фонд (mutual fund), и тогда управляющий фондом сделает всё за вас.

Допустим, что вы выбрали способ инвестиций через ПИФ и теперь хотите понять, какой фонд обеспечит лучшее сочетание риска и доходности. Хоть прошлая доходность и не гарантирует успехов в будущем, всё равно имеет смысл посмотреть, какой доход получили другие инвесторы фондов.

Чтобы пример был жизненным, я собрал данные о доходности трёх российских ПИФов акций с ноября 2015-го года по сентябрь 2020-го. Назовём эти фонды «красный», «жёлтый» и «зелёный». Ноябрь 2015-го выбран не случайно, потому что именно тогда я сформировал свой собственный портфель акций на Московской бирже. Так что к сравнению трёх ПИФов можно добавить и фонд под кодовым названием «автор».

Выяснилось, что за пять лет красный фонд заработал для своих клиентов 104%, жёлтый заработал 85%, а зелёный — 84%. Портфель автора вырос на 100%. Стоит ли похвалить управляющих фондами? Будет ли довольна супруга автора, когда он будет хвастаться результатами?

Поскольку моя супруга училась на том же факультете, что и я, и не менее въедливо смотрит на цифры, то наверняка она задаст мне несколько вопросов. Во-первых, сколько бы мы заработали, если бы держали деньги на депозите (в безрисковом активе)? Во-вторых, на сколько за это время вырос весь рынок акций? В-третьих, и в-главных, какой риск мы на себя взяли и какое соотношение риска и доходности получили?

На первые два вопроса ответить нетрудно. За рассматриваемый период индекс полной доходности МосБиржи (плюс дивиденды минус налоги) вырос на 117%. Ключевая ставка ЦБ, которую я взял как приближение безрисковой ставки, дала бы 50%. На рисунке 3.1 представлены результаты фондов, индекса и безрисковой ставки.

Рис. 3.1: Доходности фондов, индекса и безрисковой процентной ставки. Данные: [Mos20], [CBR20], вычисления автора.

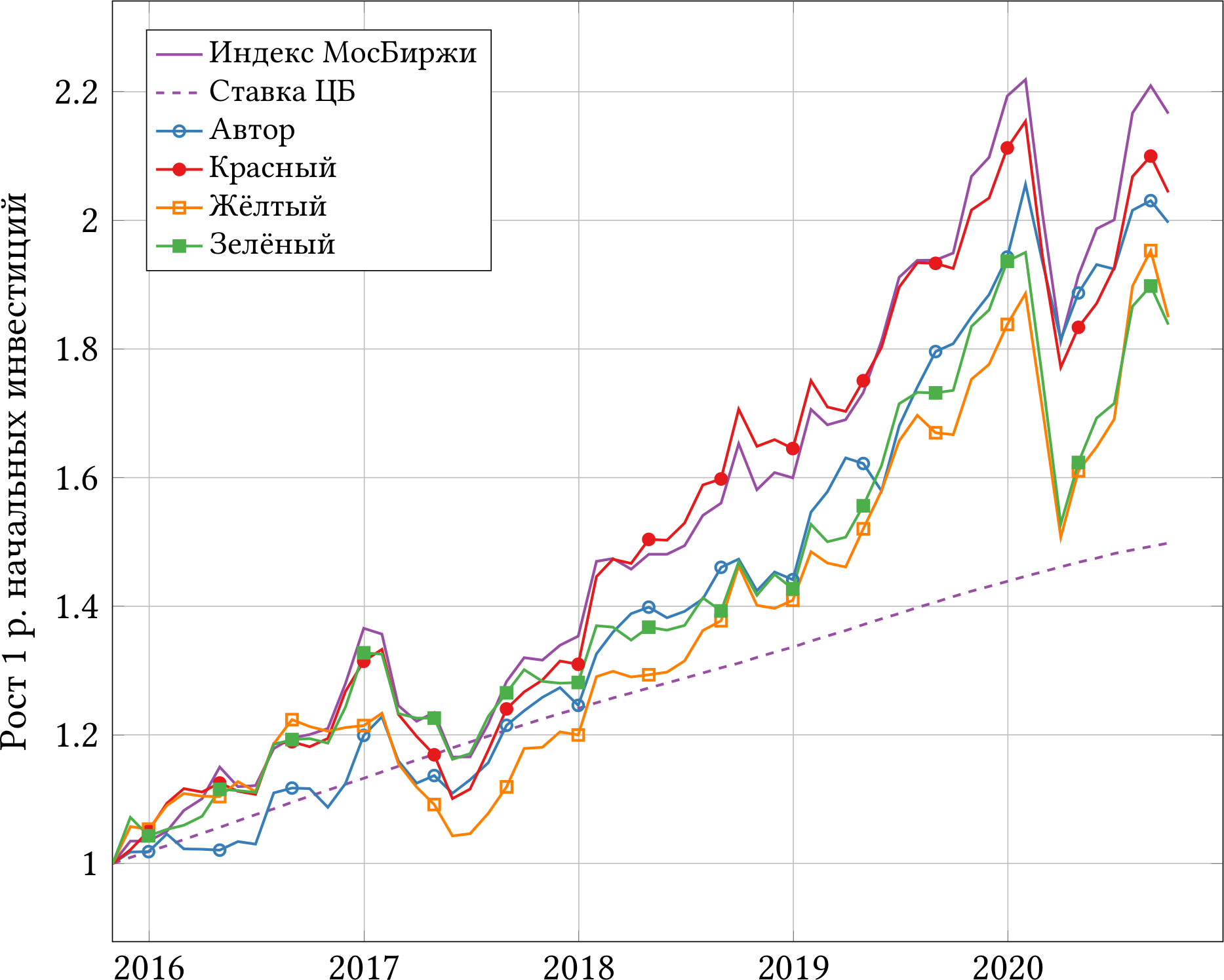
Чтобы ответить на третий вопрос о риске, придётся потрудиться. Вспомним, что по CAPM (2.2) средняя доходность любого актива или портфеля активов зависит только от «беты» и доходности рынка. Обозначим доходность фонда R_fund, а его «бету» — ?_fund.

$$

Как узнать «бету» фонда? Нет ничего проще. Сначала посчитаем исторические месячные доходности фонда R_fund,t (t — номер месяца), индекса R_mkt,t и безрискового актива R_free,t. Затем оценим следующую линейную регрессию (чуть ниже я поясню, что это такое, если вы не в курсе или забыли):

$$

Объяснить суть линейной регрессии на пальцах проще всего графически. Посмотрите на рисунок 3.2. На оси x отложены месячные доходности индекса сверх безрисковой ставки, а на оси y — месячные избыточные доходности красного фонда (красные квадратики) и портфеля автора (синие кружки). Например, если вы видите красненький квадратик с координатами (7.9%,9.7%), то был месяц (январь 2018-го, если это важно), когда индекс вырос на 7.9% выше безрисковой процентной ставки, а красный фонд — на 9.7%.

Рис. 3.2: Связь доходностей фондов с доходностью индекса. Данные: [Mos20], [CBR20], вычисления автора.

Невооружённым глазом видна зависимость: в те месяцы, когда индекс показывает рост, портфели фондов тоже растут. Когда индекс падает, портфели фондов тоже обычно падают.

Чтобы выразить это наблюдение численно, можно задать следующий вопрос. Предположим, что доходность красного фонда связана с доходностью индекса простым линейным соотношением y = ? + ?x. Какие коэффициенты ? и ? нужно подставить в это уравнение прямой, чтобы прямая проходила «ближе всего» ко всем красным квадратикам на графике? Ответ: лучше всего подойдёт прямая y = ?0.05 + 0.92x, то есть ? = ?0.05 и ? = 0.92.

Поздравляю, вы только что построили линейную регрессию методом наименьших квадратов (ordinary least squares, OLS)! За деталями того, каким алгоритмом можно вычислить коэффициенты ? и ?, отсылаю вас к любому учебнику эконометрики, например [Ver12, ch. 2]. Если решить аналогичную задачу и для остальных фондов, то получится таблица 3.1.

Таблица 3.1: Регрессия избыточных доходностей фондов на избыточную доходность индекса. 59 месячных наблюдений 11.2015–09.2020. Значения ? и ? для месячных доходностей. Отношения Шарпа и Сортино сконвертированы в годовое выражение умножением на sqrt(12). Данные: [Mos20], [CBR20], вычисления автора.

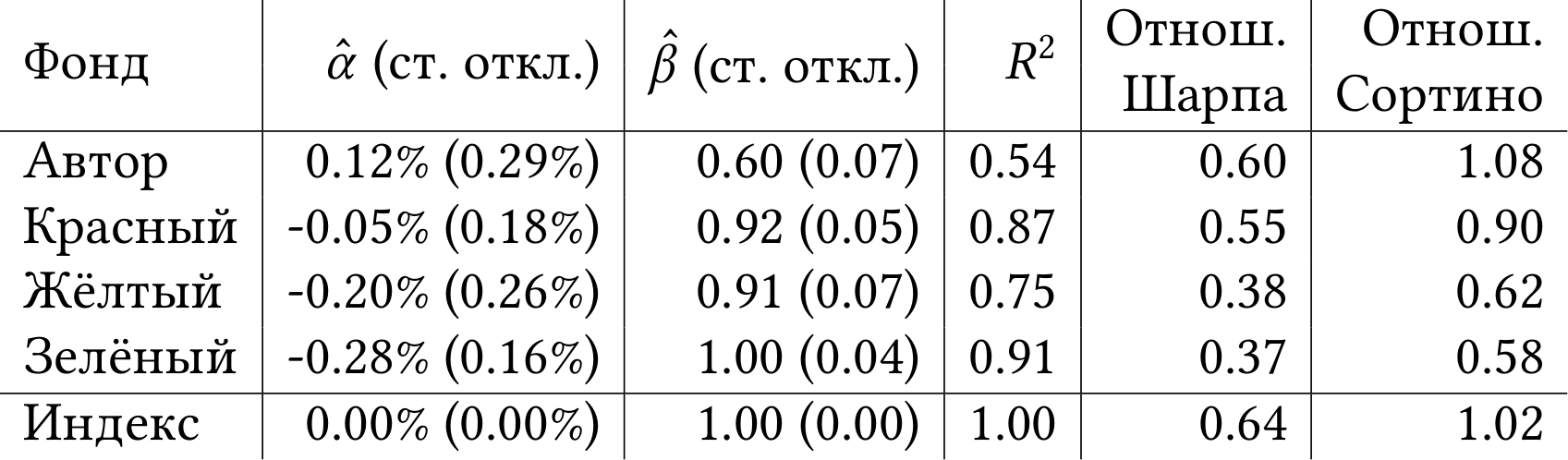
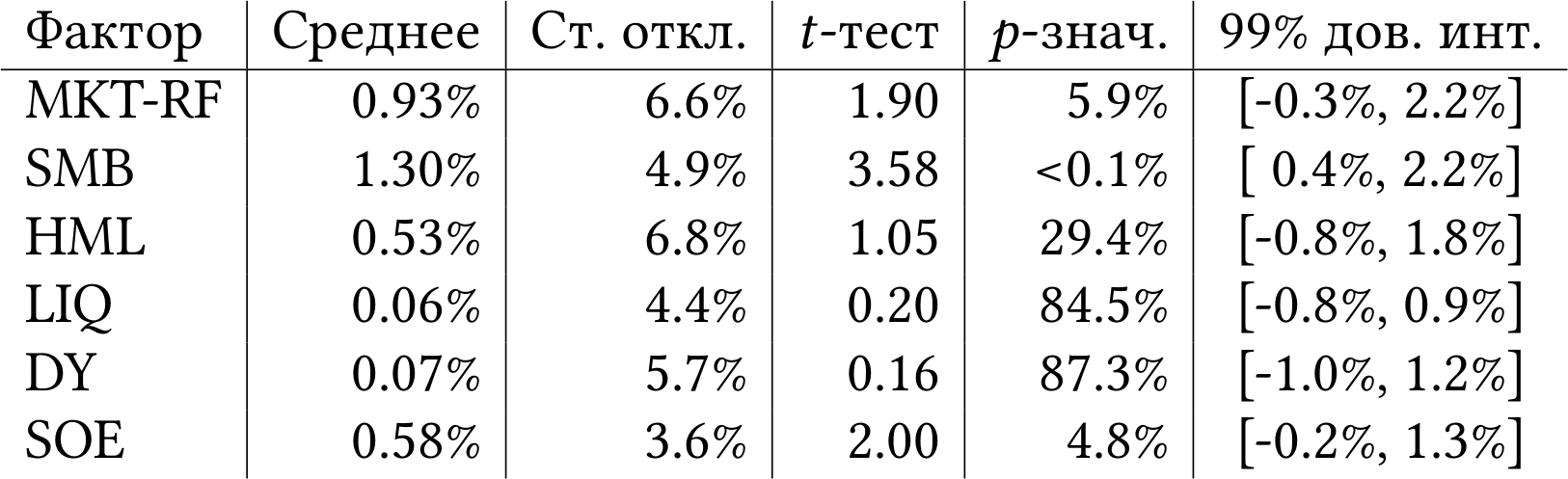
Как интерпретировать таблицу 3.1? Начнём с «беты». Например, «бета» красного фонда оказалась равной 0.92. Это наша оценка «беты» красного фонда по CAPM. В среднем, когда весь рынок (индекс) давал избыточную доходность выше безрисковой ставки 1%, красный фонд давал избыточную доходность 0.92%. Это мера систематического рыночного риска, который взял управляющий красным фондом.

Теперь посмотрим на «альфу». По CAPM, никакой «альфы» нет и быть не может, потому что доходность фонда зависит исключительно от «беты» и доходности рынка. Если какой-то фонд имеет положительную «альфу», то фонд зарабатывает больше, чем можно было бы ожидать при том же уровне систематического рыночного риска. Если «альфа» отрицательная, то вкладчики фонда получают меньшую компенсацию за систематический риск, чем можно было бы ждать по CAPM.

Интересно, что во всех трёх ПИФах «альфа» оказалась отрицательной. А вот портфель автора обогнал CAPM и зарабатывал дополнительные 0.12% в месяц сверх ожидаемой рыночной премии за риск. Кому-то может показаться, что 0.12% — это копейки. Возражу, что 0.12% в месяц — это почти 1.5% дополнительной доходности в год, что совсем неплохо. Да и в конце концов, пусть «альфа» маленькая, зато своя!

Скептик возразит, что при стандартном отклонении 0.29% значение «альфы» 0.12% статистически не отличается от нуля. Это правда, и с этим невозможно спорить. Такова реальность финансовых рынков. Зачастую у вас нет достаточно длинной истории наблюдений, чтобы получить статистически значимые оценки. Если подождать ещё лет 15 и накопить побольше данных, то, быть может, получится подтвердить, что «альфа» автора статистически значима. Но принимать инвестиционное решение и выбирать фонд вам нужно сейчас, а не через 15 лет! Так что придётся смотреть на те данные, что у нас есть.

Линейная регрессия выдаёт ещё один интересный параметр — R², он же эр-квадрат (R-squared) или коэффициент детерминации (coefficient of determination). R² принимает значения от 0 до 1. Неформально, это доля дисперсии (колебаний) доходности фонда, которую можно объяснить линейной моделью. Ещё более неформально, R² показывает, насколько хорошо прямые линии с рисунка 3.2 приближают облако точек.

Например, регрессия для зелёного фонда показала R² 0.91. Можно интерпретировать это так, что 91% колебаний доходности зелёного фонда объясняется колебаниями доходности рынка, и только 9% — действиями управляющего. Вместе с «бетой» около единички и отрицательной «альфой» это создаёт не самую хорошую картину. Вкладчики зелёного фонда взяли на себя тот же систематический риск, что и в индексе, но при этом недополучили премию за риск на 3.3% в год.

Сложно сказать, связан ли такой результат зелёного фонда с высокой комиссией за управление или с конкретными инвестиционными решениями управляющего. Но если бы клиенты зелёного фонда могли купить все акции в индексе МосБиржи, то они получили бы доходность на 3% годовых выше при том же уровне систематического риска. Запомним эту мысль.

Факторные портфели

Что ни говори, результат авторского портфеля из таблицы 3.1 выглядит подозрительно. Положительная «альфа». Относительно невысокая «бета» (чувствительность к систематическому рыночному риску). А главное, R² в районе 0.5, то есть только половину колебаний портфеля автора можно связать с движениями всего рынка.

Нет ли здесь подвоха? Да, в рамках CAPM единственный риск, за который можно заработать премию — это систематический рыночный риск. Да, движения рынка неплохо объясняют колебания портфеля автора. Но что, если CAPM говорит нам не всю правду, и на рынке есть другие систематические риски, за которые можно заработать премию за риск? Вдруг автор сделал ставку на такой риск, который не входит в CAPM, и именно этим объясняется его мнимый успех? Стоит разобраться в этом вопросе, прежде чем вставать в очередь желающих доверить автору деньги в управление.

Довольно давно исследователи заметили на рынке акций США аномалии, которые нельзя объяснить CAPM. Вот некоторые из них.

Во-первых, эффект размера (size effect). Замечено, что акции маленьких компаний растут лучше, чем акции крупных компаний (разумеется, при одинаковой «бете»).

Во-вторых, эффект стоимости (value effect). Для каждой компании можно посчитать две разных стоимости. Первая — рыночная стоимость (market value), то есть рыночная цена одной акции, умноженная на количество акций. Вторая — бухгалтерская стоимость (book value), то есть оценка акционерного капитала из финансовой отчётности. Все акции на рынке можно грубо разделить на акции стоимости (компании с высоким отношением book value / market value) и акции роста (компании с низким отношением book value / market value).

Заезженный пример компании стоимости — коммунальные сети с понятными физическими активами. Не менее заезженный пример компании роста — интернет-гигант, у которого значительная часть активов нематериальна и не отражена в бухгалтерском балансе. Так вот, эффект стоимости заключается в том, что акции стоимости приносят более высокую доходность, чем акции роста (опять же, при равной «бете»).

В-третьих, эффект инерции (momentum effect). Оказывается, что акции, которые выросли в прошлом году, с большей вероятностью будут расти и в этом. С другой стороны, акции, упавшие в прошлом году, с большей вероятностью продолжат падать и в этом.

Чтобы оценить эти эффекты численно, можно составить так называемые факторные портфели (factor portfolios). Факторный портфель — это специальная комбинация из купленных и проданных в короткую акций, которая зарабатывает деньги за счёт одного их перечисленных эффектов.

Чтобы составить портфель SMB (Small Minus Big), инвестор должен отсортировать все компании на рынке по размеру (рыночной капитализации) и разделить список пополам. В одной половине окажутся акции, которые мы назовём маленькими, а во второй окажутся акции, которые мы назовём большими. Осталось купить по списку все маленькие акции и продать в короткую все большие. Если эффект размера существует, то купленные маленькие акции принесут больший доход, чем проданные большие акции.

Для портфеля HML (High book/market Minus Low book/market) нужно отсортировать компании по отношению book/market, то есть бухгалтерского капитала к рыночной капитализации. После этого нужно купить треть акций с самым высоким отношением book/market (акции стоимости) и продать в короткую треть акций с низким отношением book/market (акции роста). Если мы правы насчёт эффекта стоимости, то акции стоимости обгонят акции роста, и портфель принесёт прибыль.

Аналогично, для портфеля MOM (MOMentum) нужно купить 30% лучших акций прошлого года и продать в короткую 30% худших. Опять-таки, портфель будет зарабатывать деньги, если эффект инерции работает, и прошлогодние победители действительно обгонят прошлогодних проигравших.

Строго говоря, процедура построения портфелей SMB, HML и MOM чуточку сложнее, чем я описал. Однако это технические детали, которые только запутают изложение. Подробности можно посмотреть в книге [BEM16, ch. 9–11] или на сайте профессора Френча [Fre20], с которого также можно скачать исторические доходности факторных портфелей.

Как бы то ни было, у нас есть портфели из акций, которые могут заработать нам деньги за счёт эффектов размера, стоимости и инерции. Чтобы составить эти портфели, достаточно уметь сортировать акции по простому критерию и делить отсортированный список на части. Почти как в анекдоте — сортируй и дели! С этой задачей справится и пятилетний ребёнок, и компьютер. Было бы странно, если бы настолько бездумно и механически составленные портфели давали положительную доходность, не так ли?

Как бы не так! На рисунке 3.3 и в таблице 3.2 представлены исторические доходности трёх факторных портфелей на рынке США. Как видите, на дистанции 94-х лет все три портфеля дали рост. Интерес к эффектам размера, стоимости и инерции возник не на пустом месте.

Рис. 3.3: Историческая доходность факторных портфелей. Данные: [Fre20].

Таблица 3.2: Годовые доходности факторных портфелей, 1927–2020. Данные: [Fre20].

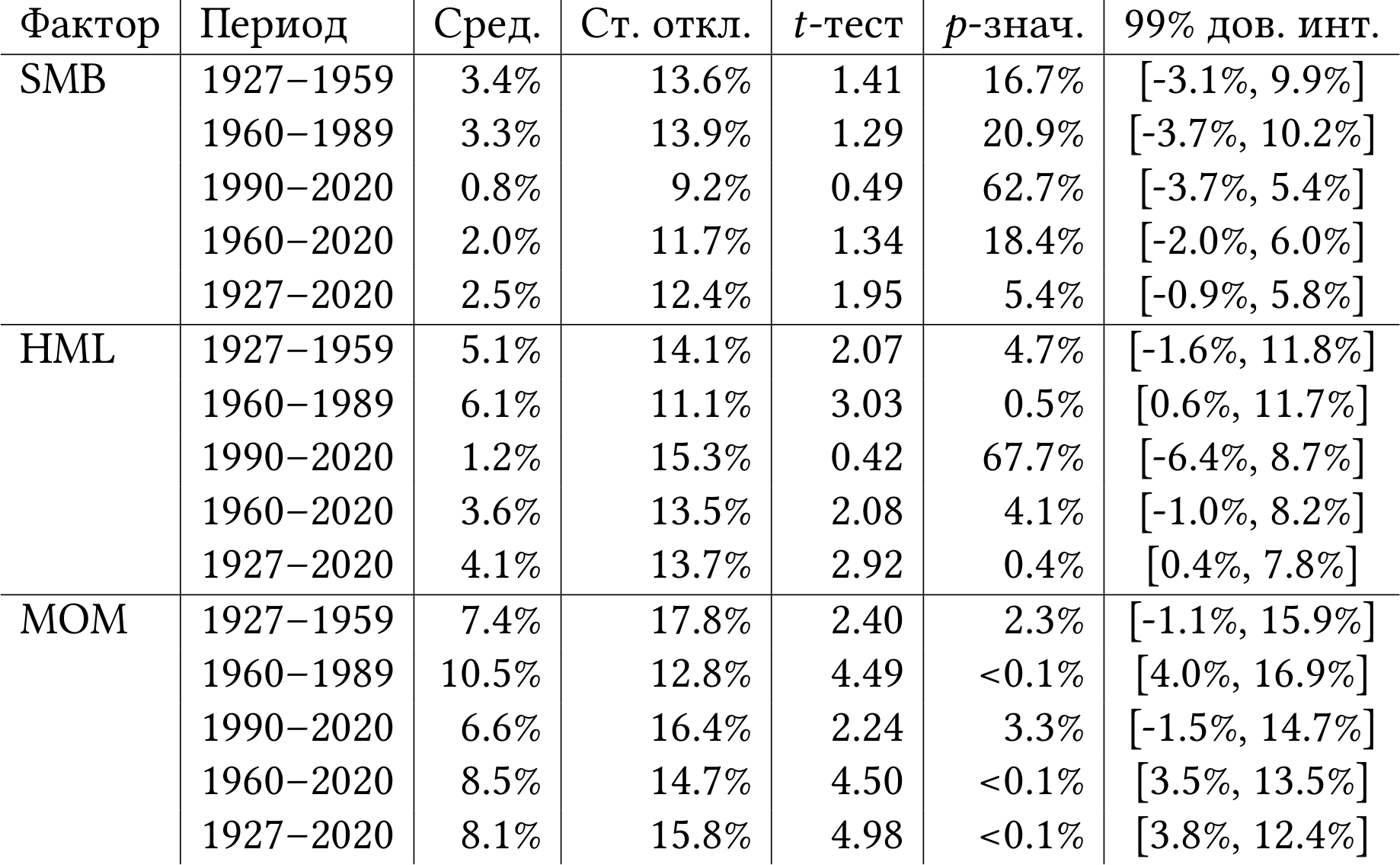
Что можно сказать о таблице 3.2 помимо того, что за столетие факторные портфели приносили доход?

Во-первых, мы не можем отвергнуть гипотезу, что на самом деле портфель SMB (маленькие компании против больших) имеет нулевую доходность. Справедливости ради, до начала 1990-х, когда Юджин Фама (Eugene Fama) и Кеннет Френч (Kenneth French) опубликовали свою известную работу [FF93] о факторах SMB и HML, доходность портфеля SMB была статистически значимой на уровне значимости 5%. В последние же 30 лет портфель SMB растёт (средняя доходность положительная), но этот рост настолько волатильный, что мы не можем уверенно утверждать, что положительная доходность — не случайность. Решайте сами, что это значит для эффекта размера.

Во-вторых, в период 1990–2020 гг. доходность всех трёх портфелей оказалась ниже, чем в среднем в истории. Возможно, это просто совпадение. Возможно, слишком много людей прочитали статьи Фамы-Френча о факторах HML и SMB, а также Марка Кархарта (Mark Carhart) о факторе MOM [Car97]. В результате, например, спрос на маленькие акции в портфеле SMB вырос, из-за чего выросла их цена и снизилась ожидаемая доходность.

Возможно, что-то фундаментально изменилось. Например, мы вошли в эпоху IT-гигантов, которые все как на подбор относятся к компаниям роста из-за околонулевой бухгалтерской стоимости нематериальных активов. Поэтому мы видим снижение доходности портфеля HML, в который эти IT-гиганты входят со знаком «минус». Сложно сказать, какое объяснение верное. Напомните мне вернуться к этому вопросу в 2050-м году.

Напоследок, ещё пара замечаний о факторных портфелях.

Во-первых, факторные портфели имеют (точнее, имели в прошлом) положительную доходность только в среднем. Нет гарантии, что доходность будет положительной каждый год. Вполне может оказаться, что в какой-то год маленькие акции проиграют большим, акции стоимости проиграют акциям роста, прошлогодние победители проиграют прошлогодним проигравшим. Не стоит рассматривать факторные портфели как машинку для зарабатывания денег без риска.

Во-вторых, факторные портфели — это скорее теоретическая конструкция, чем реальная инвестиционная стратегия. Чтобы сделать ставку, скажем, на портфель SMB, вам нужно продать в короткую большие акции, которых у вас нет, а на вырученные деньги купить маленькие акции. В теории, такой портфель не требует никаких начальных инвестиций, и его можно собрать по щелчку пальцев, не потратив ни цента.

На практике, брокеры, конечно, предоставляют своим клиентам услугу коротких продаж (когда брокер берёт взаймы акцию у другого клиента и одалживает её вам). Однако эта услуга отнюдь не бесплатная и распространяется далеко не на все акции. Вдобавок, многим инвесторам, таким как паевые фонды, короткие продажи просто-напросто запрещены законом.

Так что я с трудом представляю себе управляющего фондом, который в реальной жизни собрал бы портфель SMB. Впрочем, практическая ценность SMB и других портфелей не в этом. В чём — читайте дальше.

Многофакторная модель оценки успеха управляющих

Итак, у нас есть три портфеля, SMB, HML и MOM. Предположим, что они на самом деле имеют положительную ожидаемую доходность. Как примирить это с нашей идеей, что заработать премию можно только за систематический риск? Нет ничего проще. Нужно постановить, что факторные портфели отвечают за иные виды систематического риска, не связанные с систематическим рыночным риском из CAPM.

Если бы мы занимались теоретической наукой, то нам пришлось бы искать объяснение, почему рациональные инвесторы с какой-то там функцией полезности требуют и получают премию за риск, например, компаний стоимости и портфеля HML. Это, конечно, важно для науки, но не столь важно для нашей задачи оценки управляющих. Здесь мне близок подход некоторых физиков к квантовой механике: «Заткнись и считай!» («Shut up and calculate!»). Я не знаю, какой риск изображают факторные портфели, но это не мешает мне использовать их для расчётов.

Вспомним линейную регрессию (3.1), по которой мы оценивали доходность фондов. Дополним её ещё несколькими объясняющими переменными. А именно, для каждого периода t посчитаем гипотетические доходности портфелей SMB, HML и MOM — R_smb,t, R_hml,t и R_mom,t соответственно. Тогда у нас получится регрессия, которую называют четырёхфакторной моделью Фамы-Френча-Кархарта:

$$

Идея ровно та же, что и в предыдущей регрессии. Мы хотим посмотреть, как доходность фонда связана с доходностями четырёх факторных портфелей: уже знакомого нам рыночного портфеля из CAPM (который мы приближаем индексом акций) и трёх новых факторных портфелей SMB, HML и MOM.

Например, если мы вычислим, что ?_smb > 0, то это означает, что управляющий фондом сделал ставку на эффект размера. Конечно, вряд ли он собрал портфель SMB в чистом виде (как я говорил, это крайне сложно сделать на практике). Скорее всего, он купил в портфель больше маленьких акций, чем больших. Поэтому в те периоды, когда портфель SMB показывал рост, портфель управляющего тоже показывал дополнительный рост относительно CAPM.

Коэффициент ?_smb имеет тот же смысл, что и обычная «бета» к рынку ?_mkt. Скажем, если ?_smb = 1.5, то при росте портфеля SMB на 1% (маленькие акции в среднем выросли на 1% выше, чем большие) портфель управляющего при прочих равных растёт на 1.5%. Если портфель SMB падает на 1% (маленькие акции отстали от больших на 1%), то при прочих равных портфель фонда теряет 1.5%.

Говоря ещё проще, все четыре «беты» из регрессии (3.2) показывают, какой систематический риск (или риски) взял на себя управляющий фондом. «Альфа» говорит, заработал ли он что-то сверх премии за эти систематические риски. Положительная «альфа» в четырёхфакторной модели означает, что управляющий фондом делает что-то ещё помимо ставок на рост рынка и эффекты размера, стоимости и инерции.

Плохая новость: согласно ещё одной известной работе Фамы и Френча [FF10], средняя «альфа» американских паевых фондов по четырёхфакторной модели составляет -1.1% в год после вычета комиссий. К сожалению, средний инвестор в паевой фонд получает меньшую компенсацию за систематический риск, чем мог бы.

Готов поспорить, что вам теперь не терпится проверить на прочность положительную «альфу» авторского портфеля, прогнав её через многофакторную модель. Вполне понимаю ваше желание. Впрочем, зная цифры, я предпочту оттянуть бесславный конец и вставить в статью ещё один занудный теоретический раздел.

Арбитражная теория ценообразования (APT)

Почему вообще мы решили записать многофакторную регрессию (3.2)? Если помните, за однофакторной регрессией (3.1) стояла стройная теория CAPM (ну, я по крайней мере попытался стройно её описать). Эта теория гласит, что избыточная доходность любого портфеля должна быть пропорциональна избыточной доходности рынка.

Есть ли теоретические соображения за четырёхфакторной регрессией, которые бы объясняли, почему доходность портфеля должна зависеть, скажем, от фактора SMB? Ведь если их нет, то не занимаемся ли мы дата майнингом (data mining), бездумно закидывая в топку линейной регрессии всё больше объясняющих переменных?

Такое теоретическое объяснение есть, и оно называется арбитражная теория ценообразования (arbitrage pricing theory, APT).

В чём суть APT? На рынке всегда есть участники, которые называются арбитражёрами (arbitrageurs). Арбитражёры пристально следят за тем, чтобы цены не выходили из равновесия. Если они видят, что акция A безосновательно подешевела относительно акции B, то они купят акцию A и продадут акцию B, чтобы заработать на этом. При этом спрос на акцию A вырастет, как и её цена. Предложение акции B увеличится, и её рыночная цена упадёт. В результате ошибка рынка исчезнет, а арбитражёры заработают прибыль. Такая возможность заработать на ошибке рынка называется арбитраж (arbitrage).

Поскольку по рынку всегда бродит множество алчных арбитражёров, которые выискивают малейшие ошибки рынка, то возможности для арбитража, если они и возникают, пропадают очень быстро. Согласно крылатой фразе, на рынке нет бесплатных обедов (there is no free lunch).

Давайте я изложу этот аргумент чуть более формально, пользуясь идеей из книги [Coc05, ch. 9.4].

Предположим, что на рынке есть в общей сложности n факторов систематического риска, за которые можно заработать премию за риск. Пусть у нас есть n факторных портфелей P₁,...,P_n, каждый из которых изображает (proxy) один из этих факторов. Обозначим доходности этих портфелей (премии за риск) R₁,...,R_n. Тогда ожидаемая доходность любого актива R_asset должна быть равна

$$

Предположим, что это не так, и существует актив с положительной «альфой» в регрессии:

$$

Что сделает алчный арбитражёр, наткнувшись на такую явную ошибку рынка? Разумеется, он сразу же купит этот актив и продаст все факторные портфели в количествах ?₁, ?₂ и так далее до ?_n. Какую доходность R он получит?

$$

В правой части у нас сумма констант ? и R_free и случайной величины ?, которая является ошибкой регрессии (3.4). Чем точнее факторные портфели приближают актив (чем лучше R² регрессии), тем меньше стандартное отклонение ошибки регрессии ?_?, то есть меньше риск арбитражёра. С другой стороны, чем больше ?, тем выше его потенциальная доходность.

Получается, что чем больше ошибка рынка, и чем лучше факторные портфели приближают актив, тем лучшее соотношение доходности и стандартного отклонения (отношение Шарпа) получит арбитражёр. Арбитражёр никогда не пройдёт мимо ошибки рынка, которая обещает прибыль с хорошим отношением Шарпа. Если цены сильно отклонятся от равновесия (3.3), то арбитражёры тут же налетят как коршуны и исправят это недоразумение.

Как видите, APT исходит из иных предпосылок нежели CAPM. В CAPM мы выводили доходности активов исходя из свойств рациональных инвесторов. В APT мы сравниваем активы друг с другом и говорим, что активы с одинаковой доходностью (актив с одной стороны и комбинация факторных портфелей с другой) не могут стоить разных денег. Это называется закон одной цены (law of one price).

Можно ещё сказать, что APT оценивает активы друг относительно друга, а не в абсолютном выражении. Например, APT говорит, что два сорта нефти, Brent и WTI, должны стоить более-менее одинаковых денег. Не должно быть такого, что WTI стоит $1 000 за баррель, а Brent всего $10. Однако APT не говорит, сколько же должен стоить баррель нефти: $10 или $1 000.

С точки зрения практики, в APT можно добавить почти сколько угодно факторов риска. Главное, чтобы факторы были представлены портфелями торгуемых активов. У управляющего фондом должна быть хотя бы гипотетическая возможность купить факторный портфель. Факторы размера (SMB), стоимости (HML) и инерции (MOM) удовлетворяют этому правилу. А вот, скажем, фактор «средняя температура января» — нет, хотя он и может влиять на цены акций энергетических компаний.

Стоит отметить, что хоть мы и рассматривали, в основном, акции, идеи APT и факторного анализа доходности можно применить и к другим классам активов. Например, если вы оцениваете результаты управляющего фондом облигаций, то вам нужно выбрать соответствующие факторы.

Во-первых, вам нужно будет выбрать релевантный индекс облигаций. Во-вторых, неплохо добавить в регрессию факторы, основанные на форме кривой доходности и кредитном рейтинге. Скажем, за форму кривой доходности будет отвечать портфель «десятилетние облигации минус годовые облигации», а за кредитный рейтинг — портфель «облигации с рейтингом BBB минус облигации с рейтингом AAA».

В целом, человечество придумало сотни, если не тысячи, факторных портфелей, которые можно применить в той или иной ситуации. Это чрезвычайно полезно, когда вы хотите понять, какой риск вы (или ваш управляющий) взяли на себя.

Согласно одной из радикальных точек зрения, никакой «альфы» на самом деле нет, а есть только «беты», которые мы не видим. Если кто-то заработал «альфу», то есть доход, превышающий предсказание модели, то первым делом стоит проверить, а не скрывается ли за этой «альфой» какая-то «бета». Вдруг управляющий взял на себя неизвестный нам систематический риск, и звёзды так сошлись, что в отчётном периоде премия за этот риск оказалась положительной?

Факторные портфели на российском рынке

Что ж, сколько верёвочке ни виться, а пересчитать «альфу» автора всё равно придётся. Для этого нам будут нужны факторные портфели, составленные из российских акций. Исследователи из ИПЭИ РАНХиГС проделали титаническую работу по сбору и подготовке данных и выложили на сайте «Конструктор CAPM-RU» [IPEI20] временные ряды нескольких факторных портфелей.

1. MKT-RF — доходность рынка минус безрисковая процентная ставка, как в CAPM.
2. SMB — маленькие акции минус большие акции, как у Фамы-Френча.
3. HML — акции стоимости минус акции роста, как у Фамы-Френча.
4. MOM — прошлогодние победители минус прошлогодние проигравшие, как у Кархарта (на момент написания статьи недоступен по техническим причинам).
5. LIQ (LIQuidity) — неликвидные акции минус ликвидные. Если этот портфель даёт положительную доходность, то на рынке есть премия за риск за владение неликвидными акциями.
6. DY (Dividend Yield) — акции с высокой дивидендной доходностью (отношением дивиденды/цена) минус акции с низкой дивидендной доходностью. Если доходность этого портфеля положительная, то инвесторы в «дивидендные» акции в среднем зарабатывают больше.
7. SOE (State-Owned Enterprise) — акции частных компаний минус акции компаний с государственным участием. Если доходность этого портфеля положительная, то акции частных компаний дают большую доходность, чем акции государственных компаний.

На рисунке 3.4 изображены доходности шести факторных портфелей (минус фактор MOM, для которого по техническим причинам нет данных) с 2005-го года. Рисунок 3.5 показывает те же факторы за период с 2015-го года на случай, если вы не без оснований опасаетесь, что российский рынок середины 2000-х и конца 2010-х — это две большие разницы. Наконец, в таблице 3.3 я посчитал средние доходности, стандартные отклонения и доверительные интервалы.

Рис 3.4: Доходность факторных портфелей на рынке акций России, 2005–2020. Данные:[IPEI20].

Рис 3.5: Доходность факторных портфелей на рынке акций России, 2015–2020. Данные: [IPEI20].

Таблица 3.3: Месячные доходности факторных портфелей на рынке России. 01.2005–04.2020. SOE: 01.2007–12.2019. Данные: [IPEI20].

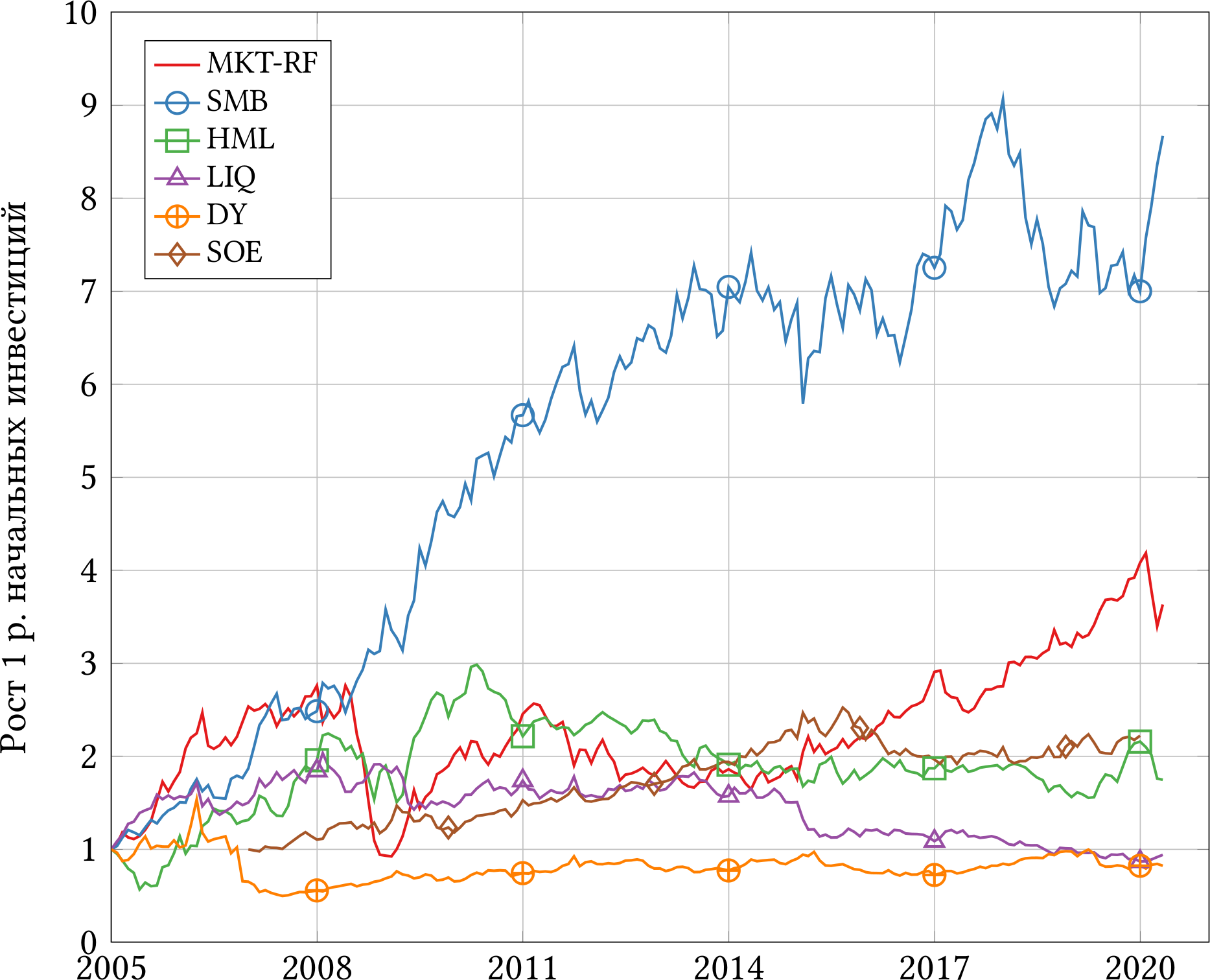
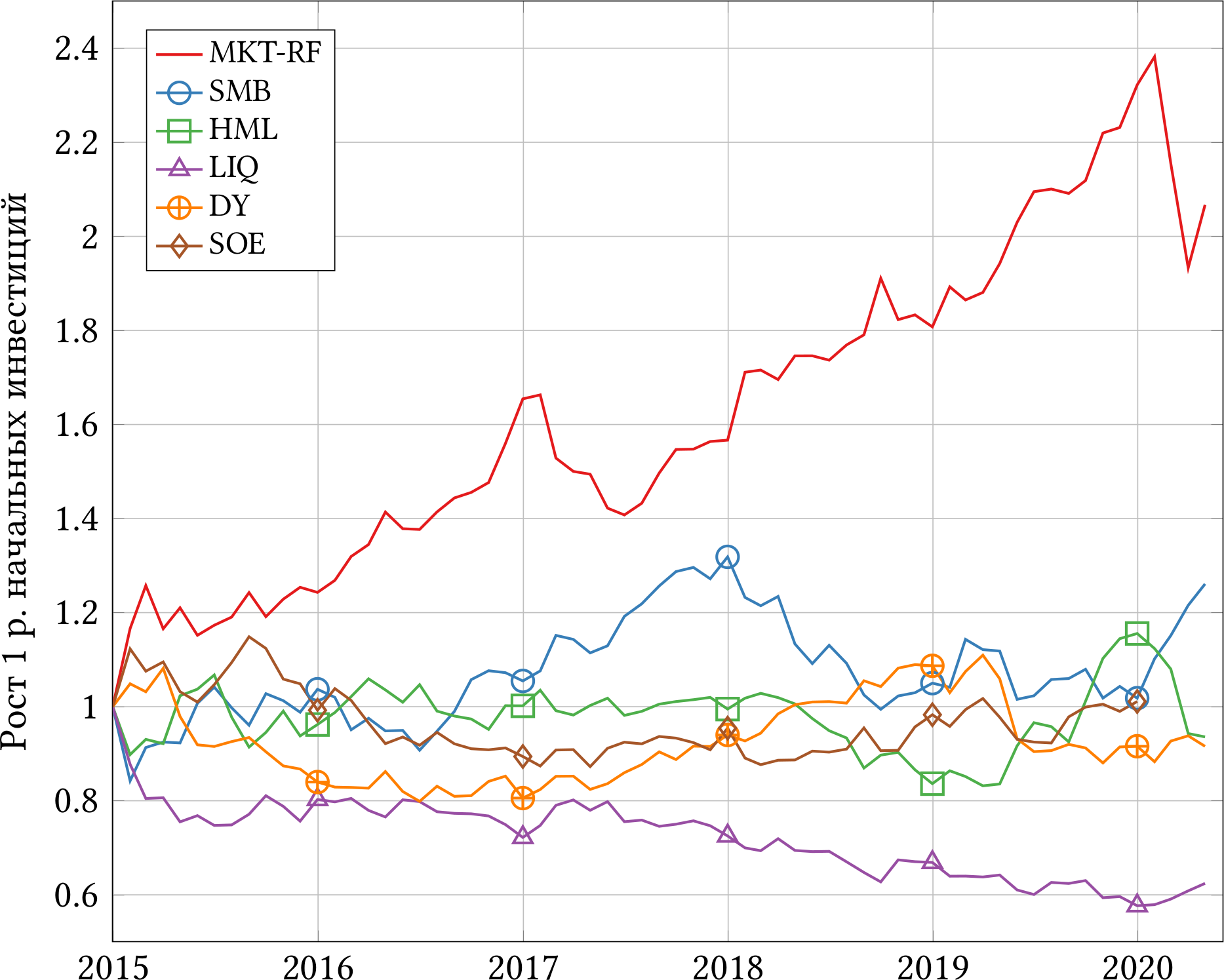
Похоже, что единственный статистически значимый фактор на российском рынке за последние 15 лет — фактор размера SMB. Маленькие акции действительно обгоняли большие. Впрочем, значительная часть роста пришлась на период до 2014-го года, а вот после 2015-го (рисунок 3.5) результаты не так впечатляют.

Если вы готовы удовлетвориться уровнем статистической значимости 10%, то с натяжкой статистически значимыми факторами являются весь рынок (MKT-RF) и фактор государственной собственности (SOE). В среднем рынок акций растёт выше безрисковой ставки, хотя мы и видели длинный период, когда роста не было. Те, кто вложился в индекс в мае 2008-го года, обогнали безрисковую ставку только к декабрю 2016-го. Частные компании на дистанции в 13 лет обогнали государственные, но в последние 5 лет (снова рисунок 3.5) мы уже не видим такой разницы в доходности.

Факторы стоимости (HML), дивидендной доходности (DY) и ликвидности (LIQ) не давали инвесторам никакой статистически значимой доходности. Для меня это открытие, потому что я довольно часто вижу и слышу советы «покупайте дивидендные акции!». Оказывается, что на дистанции этот совет не даёт дополнительной доходности. Также я бы ожидал, что уж за неликвидность-то инвесторы должны получать скидку к цене (и более высокую доходность), но нет, фактор LIQ на российском рынке не работает.

Теперь мы готовы проверить, с чем всё-таки связана положительная «альфа» авторского портфеля. Чтобы сократить изложение, я предлагаю просто сравнить результаты двух регрессий: с единственным фактором — рыночной премией за риск (как в CAPM) и с двумя факторами — рыночной премией за риск и доходностью портфеля SOE (частные компании минус государственные):

$$

Результаты обеих регрессий представлены в таблице 3.4. Сразу скажу, что остальные факторные портфели не улучшают двухфакторную регрессию из рыночного риска и SOE.

Таблица 3.4: Регрессии избыточной доходности портфеля автора на избыточную доходность рынка и доходность портфеля SOE (частные компании минус компании с гос. участием). 50 месячных наблюдений 11.2015–12.2019. Данные: [Mos20], [CBR20], [IPEI20], вычисления автора.

Случилось непоправимое. После того, как мы добавили в регрессию второй фактор систематического риска, «альфа» автора скукожилась в три раза до совершенно смешных 0.04% в месяц. Как и говорила нам APT, никакой «альфы» на самом деле и не было. Была только «бета» к фактору систематического риска, который не видела CAPM. Как только мы добавили в модель факторный портфель SOE, «альфа» пропала, а «бета» к этому портфелю вылезла на свет.

Если вы не очень поняли предыдущий абзац, то давайте ещё раз проговорим интерпретацию результатов регрессии. Анализ показал, что в те месяцы, когда портфель SOE имел положительную доходность (частные компании обогнали компании с гос. участием), портфель автора тоже рос сильнее. А именно, поскольку мы оценили «бету» к фактору SOE как 0.28, то при росте портфеля SOE на 1% в месяц, портфель автора при прочих равных рос на 0.28% в тот же месяц.

Судя по всему, в портфеле автора доля частных компаний больше, чем доля частных компаний на рынке. Именно поэтому доходность факторного портфеля SOE помогает лучше объяснить колебания доходности портфеля автора от месяца к месяцу (R², доля объяснённых колебаний, вырос). После поправки на этот фактор, «альфа» автора стала очень близка к нулю. То есть почти вся доходность автора — это банальная премия за риск. Автор сделал ставку на два вида систематического риска (рыночный риск и риск частных компаний) и заработал премию.

Особенно унизительно то, что портфель SOE — это же бездумная механическая стратегия, как, впрочем, и остальные факторные портфели. Даже пятиклассник справился бы с задачей скачать список компаний, входящих в индекс МосБиржи, выкинуть из него компании с гос. участием и купить оставшиеся частные. И этот пятиклассник заработал бы ровно ту же доходность при ровно том же уровне систематического риска, что и автор с двумя образованиями и непомерным самомнением.

Как бы то ни было, пример автора отлично демонстрирует мощь факторного анализа доходностей. Даже не зная заранее, какие конкретно акции купил автор, мы можем выдвинуть гипотезу, что его портфель перекошен в сторону частных компаний. И это правда, регрессия вывела меня на чистую воду! Поскольку в силу своих политических взглядов я без восторга отношусь к некоторым государственным компаниям и их руководителям, в моём портфеле частные компании представлены шире, чем на рынке.

Отказ от ответственности

Мнение автора статьи может не совпадать с официальной позицией Deutsche Bank AG. Статья не является предложением или рекламой какой-либо услуги. Упоминание третьих сторон не предполагает одобрения или неодобрения. Автор и Deutsche Bank напоминают, что торговля на финансовых рынках сопряжена с риском, и не несут ответственности за возможные негативные последствия ваших личных инвестиционных решений.

Список литературы

[BEM16] Turan G Bali, Robert F Engle, and Scott Murray. Empirical asset pricing: the cross section of stock returns. John Wiley & Sons, 2016. ISBN: 9781118095041.
[Car97] Mark M Carhart. “On persistence in mutual fund performance”. In: The Journal of finance 52.1 (1997), pp. 57–82.
[CBR20] Банк России. Ключевая ставка Банка России. 2020.
[Coc05] John H Cochrane. Asset pricing. Revised edition. Princeton University Press, 2005. ISBN: 0691121370.
[FF10] Eugene F Fama and Kenneth R French. “Luck versus skill in the cross-section of mutual fund returns”. In: The journal of finance 65.5 (2010), pp. 1915–1947.
[FF93] Eugene F Fama and Kenneth R French. “Common Risk Factors in the Returns On Stocks And Bonds”. In: Journal of Financial Economics 33 (1993), pp. 3–56.
[Fre20] Kenneth R French. Kenneth French Data Library. 2020.
[IPEI20] ИПЭИ РАНХиГС. Конструктор CAPM-RU. 2020.
[Mos20] Московская биржа. Индексы МосБиржи полной доходности. 2020.
[Ver12] Marno Verbeek. A guide to modern econometrics. 4th ed. John Wiley & Sons Ltd., 2012. ISBN: 9781119951674.

Все статьи цикла

Часть 1. Рациональные инвесторы. Риск и доходность. Диверсификация. Портфельная оптимизация
Часть 2. Модель CAPM. Систематический и идиосинкратический риск. Рыночная премия за риск
Часть 3. Анализ доходности фондов. Факторные модели. Арбитражная теория ценообразования
Часть 4. Биржевые фонды. Эффективность рынка. Личный опыт и сбережения на пенсию