20.12.2020 19:52
maxcoolmakarov 8 2800 Источник

Хеш-функция - это такая функция, которая осуществляет преобразование набора входных данных произвольной длины в битовую последовательность установленной длины. Хеш-функции играют важную роль в современной криптографии. Технологии развиваются, появляются новые требования к безопасности и вычислительной сложности. Лидерами среди алгоритмов хеширования во многих сферах остаются алгоритмы семейства SHA, однако есть и другое семейство алгоритмов, основанных на клеточных автоматах и заслуживающих всеобщего внимания.

Клеточные автоматы

Клеточный автомат достаточно распространенная вещь, заслуживающая отдельного поста. Однако если коротко, то это дискретная модель, представляющая собой сетку произвольной размерности, каждая клетка которой в каждый момент времени может принимать одно из конечного множества состояний, и определено правило перехода клеток из одного состояния в другое.

В случае элементарных клеточных автоматов сетки ячеек имеют одномерное измерение.

В клеточном автомате для каждой ячейки существует набор других ячеек, называемых окрестностью, которые определяют следующее состояние ячейки. Начальное состояние - это состояние, в котором определены значения ячейки и их окрестности в момент времени t. Теперь новое поколение ячеек создается, когда "t" увеличивается на 1.

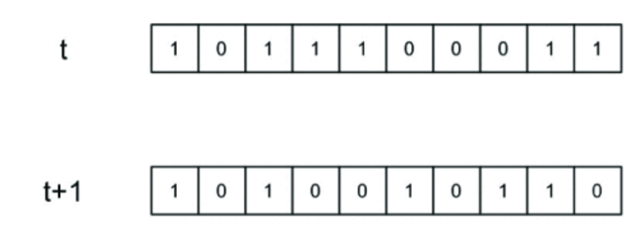
Выше представлены две соседние итерации для Правила 30, который определяется следующим образом:

C^{t+1}_s=C^t_{s-1} \ XOR \ (C^t_s \ OR \ C^t_{s+1})

Что можно для простоты интерпретировать в следующем виде:

Преимущества использования клеточных автоматов

  • Клеточные автоматы обеспечивают высокий уровень параллелизма, что позволяет достичь высоких скоростей в условиях ограниченных вычислительных ресурсов и жестких требований к энергопотреблению.

  • Обладают хорошим лавинным эффектом (малое изменение входных данных влечет полное изменение выходных).

  • Устойчивость к атакам временного анализа.

Вышеописанные преимущества сразу наталкивают на мысль использовать такие алгоритмы в интернете вещей.

Что же там под капотом?

Алгоритм получает на вход сообщение cпроизвольного размера и ключ k, размером: 128, 192 или 256 бит и возвращает хешированное значение ключа.

Базовое описание алгоритма

  1. Первоначальное сообщениеcбыть дополнено следующим образом:

    size(c) \text{ mod } 512 = 0\text{ and } size(c) >= 512

    дополнение можно производить простым заполнением недостающих разрядов нулями.

    Обозначим дополненное сообщение какC.

  2. Аналогично дополняется ключk.

    size(k) \text{ mod } 512 = 0\text{ and } size(k) >= 512

    Обозначим дополненный ключ как k

  3. Сообщение Cразбивается на блоки по 512 бит.

  4. Каждый 512 битный блок, полученный на предыдущем шаге разбивается ещё раз на 8 подблоков по 64 бита.

  5. К каждому 512 блоку применяется правило 30.

  6. Выход пункта 5 вместе с 512 битным ключом поступают в функцию трансформации (ФТ).

  7.  Этот результат подвергается операции XOR с результатом пункта 5 для следующего 512 битного блока.

  8.  Ключ для последующих раундов получается с помощью поворота ключа предыдущей итерации, который выполняет циклический сдвиг битов на 1.

  9.  Шаги 6, 7 и 8 повторяются, пока не кончатся блоки сообщения по 512 бит, то есть пока всё сообщение не будет хешировано.

Теперь рассмотрим один из вариантов реализации самой функции трансформации, для приведенной ниже функции трансформации авторам удалось добиться полного лавинного эффекта.

Функция трансформации

Для получения полностью случайного выхода по заданному входу в функции трансформации используются как клеточные автоматы, так и побитовые логические операции.

Здесь мы будем оперировать с отдельными 64 битными блоками.

  1. a=e

    Это означает, что байты из eнапрямую отображаются вa

  2. b=J(g, h, K_1) или b=J(g, h, K_5)

    Если раунд нечетный, то используется a=J(g, h, K_1) иначе a=J(g, h, K_5)

    J(x,y,z) = ((\text{ROTL}^{47}(x)\text{ XOR }\,Rule\,30(\text{ROTL}^{37}(y'))\text{ AND }((\text{ ROTR}^{17}(z)))

  3. c=G(e, f, K_2) или c=G(e, f, K_6)

     Если раунд нечетный, то используется c=G(e, f, K_2) иначе c=G(e, f, K_6)

    G(x,y,z) = (Rule134(Rule30(x'))\text{ OR } y)\text{ XOR } (Rule30(z')\text{ AND } x)

  4. d = F(a,c)

    F(x,y) = Rule30(x)\text{ XOR } y'

  5. e= J(a, d ,K_4) или e=J(a, d ,K_8)

     Если раунд нечетный, то используется e= J(a, d ,K_4) иначе e=J(a, d ,K_8)

     Функция Jопределена в пункте 1.

  6. f=H(b, d)

    H(x,y) = \text{ROTL}^{17}( x )\text{ XOR }\text{ ROTL}^{59}(y)

  7. g=I(c, f)

    I(x,y) = \text{ROTL}^{41}(x')\text{ XOR }\text{Rule134}(\text{ Rule30}(\text{ ROTL}^{31}(y')))

  8. h=H(a, K_3) или h = H(a, K_7)

     Если раунд нечетный, то используется h=H(a, K_3) иначе h=H(c, K_7)

     Функция Hопределена в пункте 4.

Где ROTL — циклический сдвиг битов влево, ROTR — циклический сдвиг битов вправо.

Внутри этой функции преобразования количество раундов распределяется динамически. Они рассчитываются по формуле:

rounds = количество '1' в блоке сообщения(512 битовом) +количество '0' в ключе (512 битовом) mod 512 .

Пару слов о безопасности

При построении функций трансформации можно обойтись и простым использованием правила 30 клеточного автомата, однако это не придаст хеш-функции полного лавинного эффекта и случайности. Поэтому оно всегда применяется в связке с другими нелинейными правилами клеточных автоматов и побитовыми операциями между ними. Такие алгоритмы хеширования достигают полного лавинного эффекта за небольшое число итераций и проходят все статистические тесты, распространяемые Национальным Институтом Стандартов и Технологий.

Ссылки и статьи по теме: