Возьмём гиперболу вида:
Здесь n - нечётное число, делители которого должны быть найдены. Умножим f(x) на cos[??f(x)] (прим. - скобки ( ) и [ ] равнозначны и не вносят дополнительных смыслов). И возьмём модуль полученной функции g(x):
![|g(x)|=|f(x)?cos[??f(x)]|](https://habrastorage.org/getpro/habr/upload_files/df6/f19/f53/df6f19f53cb770f27ae8857b578a6a3f.svg)
Графики f(x) и |g(x)| показаны на рис. 1. n при этом взято равным 15. И это один из главных недостатков метода, при больших значениях n аргумент косинуса меняется с очень высокой частотой.
![Рисунок 1 - График функций f(x)=35/x и |g(x)|=|f(x)?cos[??f(x)]|](https://habrastorage.org/getpro/habr/upload_files/e43/ea9/d01/e43ea9d01ef16cf978bee48e69743f1b.png "Рисунок 1 - График функций f(x)=35/x и |g(x)|=|f(x)?cos[??f(x)]|")
Если возвести в четную степень косинус, получим график, изображённый на рисунке 2 красным.
![Рисунок 2 - График функции f(x)?cos[??f(x)]^10](https://habrastorage.org/getpro/habr/upload_files/dfb/b26/ee0/dfbb26ee0a865751b569026b90cd015a.png "Рисунок 2 - График функции f(x)?cos[??f(x)]^10")
На последнем шаге "профильтруем" (см. рис. 3) наш косинус (т.е. умножим g(x)) функцией вида [sin(??x/2)?sin(3??x/2)?sin(5??x/2)?sin(7??x/2)]^20.
На графике будут видны все возможные делители числа n. В нашем случае это 1, 3, 5, 15.
![Рисунок 3 - Фильтрация f(x)?cos[??f(x)]^10 с помощью sin(??n?x/2)](https://habrastorage.org/getpro/habr/upload_files/003/b37/2be/003b372beb393480a1b8cb6f6a6b9c2c.png "Рисунок 3 - Фильтрация f(x)?cos[??f(x)]^10 с помощью sin(??n?x/2)")
Если взять n=105, на рисунках 4, 5 можно увидеть возможные делители 1, 3, 5, 7, 15, 21, 35. 105 не показано.
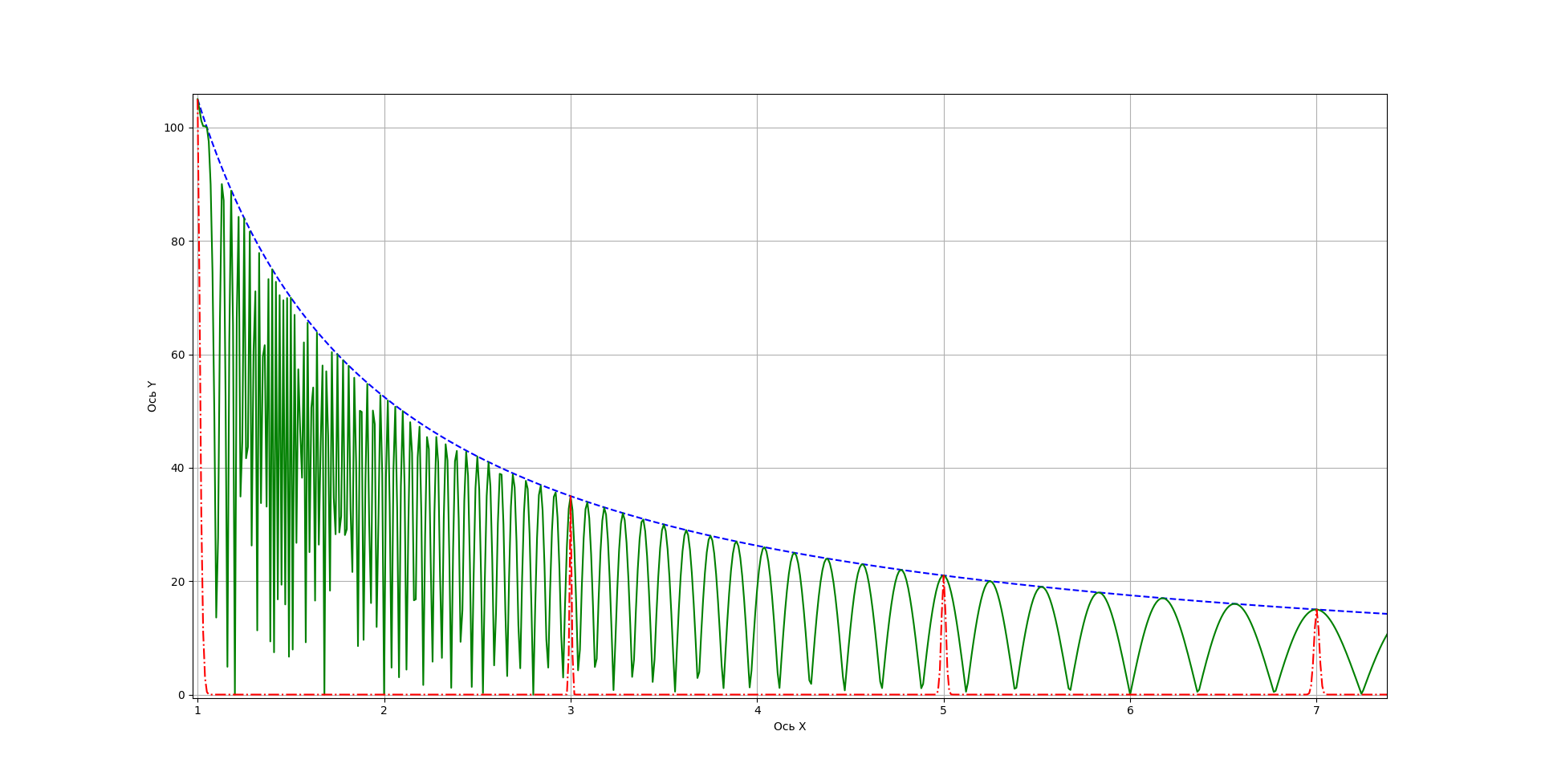
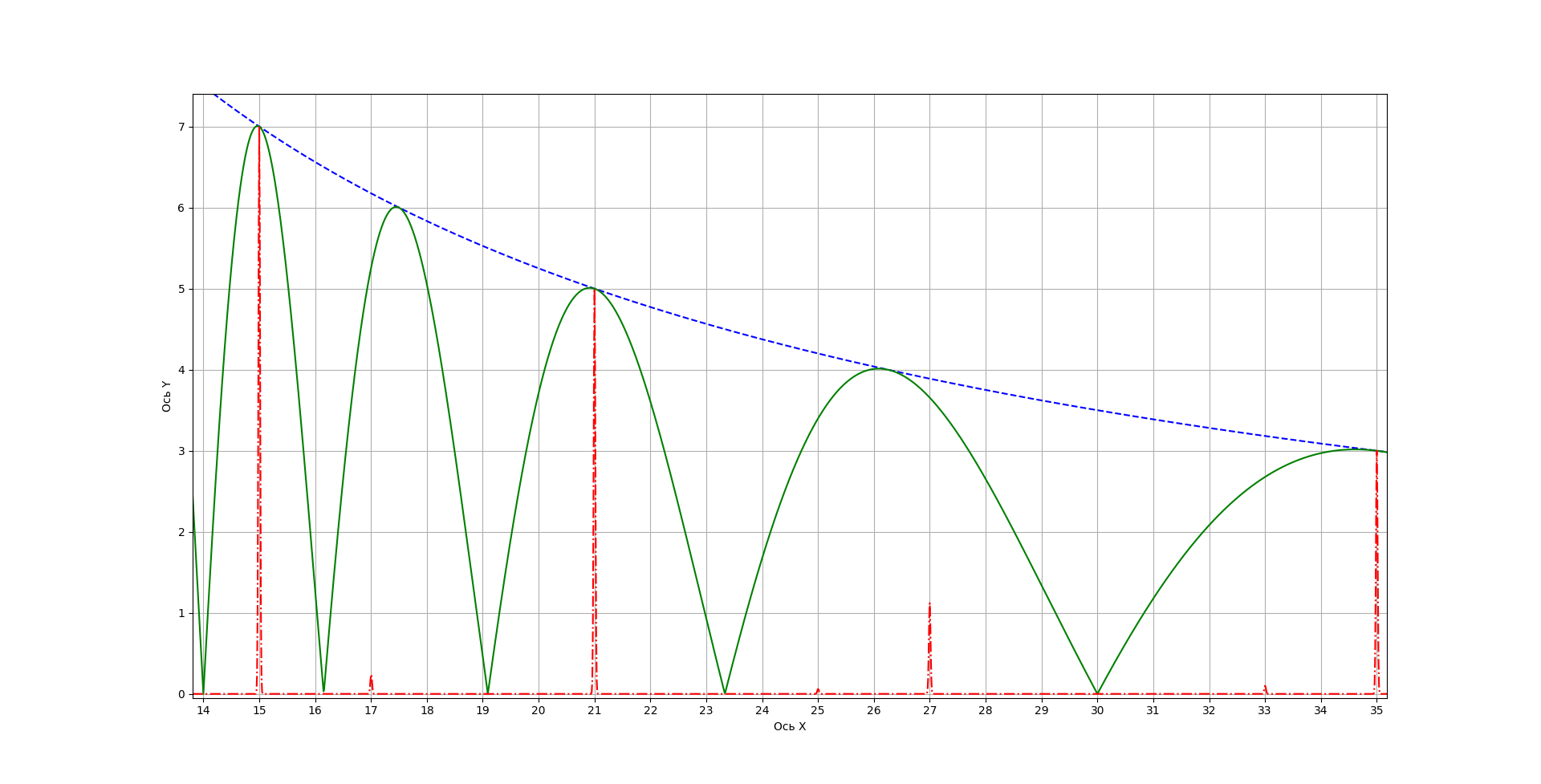
"Поиграв" степенями и аргументами синусов, можно добиться необходимой для конкретной задачи картины.
Т.к. гиперболой описывается изотермический процесс, позаимствовав из термодинамики p-V-T диаграмму, изложенное выше можно представить и в трёхмерном виде. Для красоты на рис. 6 все множители нормированы по величине 10.
Некоторые справочные данные функции (-cos[??f(x)]) :
Количество периодов на отрезке от 1 до n равно Nn=(n-1)/2
Номер периода N для координаты x можно вычислить по формуле Nx=n?(x-1)/2?x
Координата х N-го периода вычисляется по формуле xN=n/(n-2?N)
Отношение значения координаты xN+1 к xN: xN+1/xN=1+2/(n-2?N)
Если представить число достаточно большое n как произведение П(1+2/(n-2?N)) от 1 до Nn, первые ?63,2% членов при произведении дадут число е.
wataru
Вы открыли замечательное свойство косинуса: он равен +-1 при аргументе, кратному Pi. Для всех остальных аргументов — косинус меньше 1 по модулю. Это проходят в школе, где-то в 9-ом, наверно, классе.
Поэтому, возводя в четную степень cos(pi*f(x)) вы получаете пики когда f(x) — целое. Ваше f(x) = n/x, поэтому весь график будет иметь пики в рациональных x=p/q т.ч. p|n. Делители числа n тут получаются при q=1. При q>1 вы получаете бесконечное множество пиков около нуля и всякие лишние, вроде 2.5 для n=15.
Лишние рациональные числа для q>1 вы пытаетесь фильтровать, но для этого достаточно составить функцию, которая принимает 1 по модулю только в целых числах. Опять же, можно взять это свойство косинуса и домножить на сos(pi*x).
Ваша же фильтрация с домножением на много синусов не работает. Например, ваш множитель для x=3 дает почти 0 и удаляет этот делитель 15 с графика.
Домножение же только на sin(??n?x/2) оставляет любое x — нечетное целое число. Для n=15 вы все правильно отфильтруете, но для n=10 вычеркнете еще и делитель x=2.
Еще вопрос: зачем домножать на f(x) весь график? Почему бы не строить график только косинуса? Тогда все пики будут одинаковой высоты. В итоге искомая функция будет cos(pi*n/x)^20cos(pi*x)^20.
Вся эта статья напоминает мне старую байку о статье каких-то биологов, которые обнаружили удивительную закономерность — для всех муравейников, которые бы они не меряли, длина границы была примерно в 3 раза больше их ширины.
Inzer Автор
Деление на 20 в аргументе синусов исправил на 2. Опечатка. Для n уточнил нечётность, спасибо.
Готовил все по рецепту, только вместо курицы взял рыбу, вместо грибов положил бананы, а вместо пармезана — брынзу…
cos(pi*n/x)^20cos(pi*x)^20 не будет таким же, как cos x sin.
wataru
Что вам вообще надо, какая у вас задача? cos(pi*n/x)^k cos(pi*x)^k стремиться к 1 при k->бесконечности только для делителей числа n, а для всех остальных чисел — к 0. Судя по вашим графикам и заголовку статьи, именно этого вы и добиваетесь.
Ваш cos(pi n/x)^k sin(pi x / 2)^k будет точно таким же, но только для нечетных делителей числа n.
Если вам так хочется именно синус использовать, то объясните это в статье. Зачем, почему, откуда там коэффициенты 1/2, 3/2, 5/2, 7/2? Почему остановились на 7? Объясните, почему ваша функция имеет пики в делителях? Что за лишние пики и как вы их фильтруете?