03.02.2021 09:00
vdsina_m 10 4300 Источник


Примечание: полный исходный код проекта можно найти здесь.

Вы когда-нибудь задавались вопросом, как цифровой калькулятор получает текстовое выражение и вычисляет его результат? Не говоря уже об обработке математических ошибок, семантических ошибок или работе с таким входными данными, как числа с плавающей запятой. Лично я задавался!

Я размышлял над этой задачей, проводя инженерные разработки для моей магистерской работы. Оказалось, что я трачу много времени на поиск одних и тех же физических единиц измерения, чтобы проверить преобразования и правильность своих вычислений.

Раздражение от монотонной работы помогло мне вскоре осознать, что единицы и их преобразования никогда не меняются. Следовательно, мне не нужно каждый раз искать их, достаточно сохранить информацию один раз, а затем спроектировать простой инструмент, позволяющий автоматизировать проверку преобразований и корректности!

В результате я написал собственный небольшой калькулятор командной строки, выполняющий парсинг семантического математического выражения и вычисляющий результат с необходимой обработкой ошибок. Усложнило создание калькулятора то, что он может обрабатывать выражения с единицами СИ. Этот небольшой «побочный квест» значительно ускорил мой рабочий процесс и, честно говоря, я по-прежнему ежедневно использую его в процессе программирования, хотя на его создание потребовалось всего два дня.

Примечание: спроектированный мной парсер выражений является парсером с рекурсивным спуском, использующим подъём предшествования. Я не лингвист, поэтому незнаком с такими концепциями, как бесконтекстная грамматика.

В этой статье я расскажу о своей попытке создания настраиваемого микрокалькулятора без зависимостей, который может парсить математические выражения с физическими единицами измерения и ускорить ваш процесс вычислений в командной строке.

Я считаю, что это не только любопытное, но и полезное занятие, которое может служить опорной точкой для создания любой другой семантической системы обработки математических выражений! Этот проект позволил мне разрешить многие загадки о принципах работы семантических математических программ. Если вы любите кодинг и интересуетесь лингвистикой и математикой, то эта статья для вас.

Примечание: разумеется, я понимаю, что существуют готовые библиотеки для решения подобных задач, но это показалось мне любопытным проектом, для которого у меня уже есть хорошая концепция решения. Я всё равно решил реализовать его и очень доволен результатом. Примерами подобных программ являются insect, qalculate!, wcalc. Важное отличие моего решения заключается в том, что программа не требует «запуска», а просто работает из консоли.

Мой первый калькулятор командной строки


Основная задача калькулятора командной строки — парсинг человекочитаемого математического выражения с единицами измерения, возврат его значения (если его возможно вычислить) и указание пользователю на место, где есть ошибка (если вычислить его невозможно).

В следующем разделе я объясню, как на стандартном C++ в примерно 350 строках кода можно реализовать изящный самодельный калькулятор командной строки.

Чтобы алгоритм и процесс были нагляднее, мы будем наблюдать за следующим примером математического выражения:


результат которого должен быть равен 1,35 м.

Примечание: я использую квадратные скобки, потому что bash не любит круглые. Тильды эквивалентны знакам «минус», их нужно писать так, чтобы отличать от бинарного вычитания.

Синтаксис математических выражений с единицами измерения


Вычисляемое математическое выражение должно быть представлено как однозначно интерпретируемая строка символов. Для вычисления выражения нам нужно ответить на ряд важных вопросов:

  1. Как выражаются числа с единицами измерения и как с ними можно выполнять действия?
  2. Какие символы допускаются в выражении и что они обозначают?
  3. Как символы группируются для создания структур/операций с математическим смыслом?
  4. Как преобразовать выражение на основании его структуры, чтобы получить математическое вычисление?

Представление чисел и единиц измерения


Чтобы различные операции могли работать с парами «число-единица измерения», нужно задать их структуру и операторы. В следующем разделе я вкратце расскажу, как реализовать такие пары «число-единица измерения».

Единицы измерения СИ — простая реализация на C++


В международной системе единиц физические величины выражаются как произведение 7 основных единиц: времени, длины, массы, электрического тока, термодинамической температуры, количества вещества и силы света.


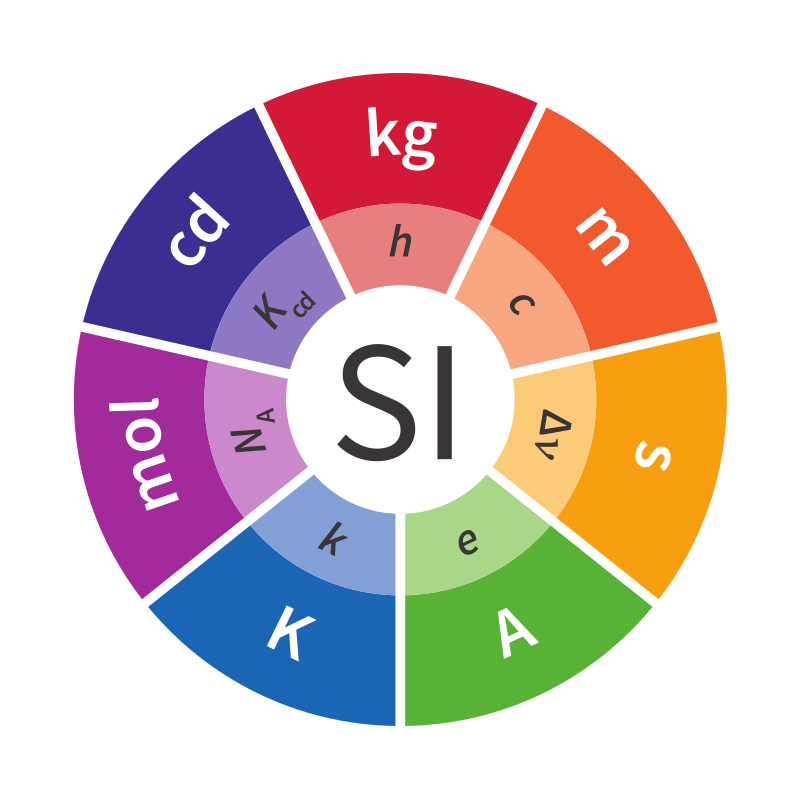
Каждую физическую величину можно создать из произведения степеней этих единиц. Мы называем полную сложную производную единицу «размерностью». Создадим структуру, отражающую этот факт, сохранив в ней вектор степеней, связанный с каждой основной единицей:

struct unit{              // Generic SI Derived-Unit

  vector<double> dim;     // Vector of base-unit powers

  unit(){};               // Constructors
  unit(dlist d){
    for(auto&e: d)
      dim.push_back(e);
  }

};

void fatal(string err){
  cout<<err<<endl;
  exit(0);
}

//Comparison Operators
bool operator==(const unit& l, const unit& r){
  if(l.dim.size() != r.dim.size())
    fatal("Dimension mismatch");
  for(int i = 0; i < l.dim.size(); i++)
    if(l.dim[i] != r.dim[i]) return false;
  return true;
}

bool operator!=(const unit& l, const unit& r){
  return !(l == r);
}

Мы можем задать каждую основную единицу как константу типа unit:

const unit D   = unit({0, 0, 0, 0, 0, 0, 0}); //No Dimension
const unit s   = unit({1, 0, 0, 0, 0, 0, 0});
const unit m   = unit({0, 1, 0, 0, 0, 0, 0});
const unit kg  = unit({0, 0, 1, 0, 0, 0, 0});
const unit A   = unit({0, 0, 0, 1, 0, 0, 0});
const unit K   = unit({0, 0, 0, 0, 1, 0, 0});
const unit mol = unit({0, 0, 0, 0, 0, 1, 0});
const unit cd  = unit({0, 0, 0, 0, 0, 0, 1});

Зададим набор перегруженных операторов для структуры единиц. Разные единицы можно умножать/делить, но нельзя прибавлять/вычитать. При сложении/вычитании одинаковых единиц получается та же единица. Единицу без размерности нельзя использовать как степень, но единицу можно возвести в степень:

unit operator+(unit l, unit r){
  if(l == r) return l;
  fatal("Unit mismatch in operator +");
}

unit operator-(unit l, unit r){
  if(l == r) return l;
  fatal("Unit mismatch in operator -");
}

unit operator/(unit l, unit r){
  if(l.dim.size() != r.dim.size())
    fatal("Dimension mismatch");
  for(int i = 0; i < l.dim.size(); i++)
    l.dim[i] -= r.dim[i];
  return l;
}

unit operator*(unit l, unit r){
  if(l.dim.size() != r.dim.size()) 
    fatal("Dimension mismatch");
  for(int i = 0; i < l.dim.size(); i++)
    l.dim[i] += r.dim[i];
  return l;
}

unit operator%(unit l, unit r){
  if(l == r) return l;
  fatal("Unit mismatch in operator %");
}

template<typename T>
unit operator^(unit l, const T f){
  for(int i = 0; i < l.dim.size(); i++)
    l.dim[i] *= f;
  return l;
}

Пары значений «число-единица»


Числа, связанные с единицами, называются «значениями» и задаются следующим образом:

struct val{
  double n = 1.0;  // Magnitude (default = unity)
  unit u;          // Dimension

  val(){};  //Dimensionless Single Value
  val(double _n, unit _u):n{_n},u(_u){};
};

bool operator==(const val& l, const val& r){
  if(l.u != r.u) return false;
  if(l.n != r.n) return false;
  return true;
}

Аналогично единицам мы зададим набор перегруженных операторов, действующих между значениями и возвращающих новое значение:

val operator+(val l, const val& r){
  l.u = l.u + r.u;
  l.n = l.n + r.n;
  return l;
}

val operator-(val l, const val& r){
  l.u = l.u - r.u;
  l.n = l.n - r.n;
  return l;
}

val operator*(val l, const val& r){
  l.n = l.n * r.n;
  l.u = l.u * r.u;
  return l;
}

val operator/(val l, const val& r){
  l.n = l.n / r.n;
  l.u = l.u / r.u;
  return l;
}

val operator%(val l, const val& r){
  l.n -= (int)(l.n/r.n)*r.n;
  l.u = l.u%r.u;
  return l;
}

val operator^(val l, const val& r){
  if(r.u != D) fatal("Non-Dimensionless Exponent");
  l.n = pow(l.n, r.n);
  l.u = l.u ^ r.n;
  return l;
}

Производные единицы как скомбинированные основные единицы


Имея строку, представляющую единицу или другую физическую величину, мы можем извлечь пару «число-единица» при помощи таблицы поиска. Значения создаются умножением основных единиц и сохраняются в map с ссылкой по символу:

map <string, val> ud = {

  //Base Unit Scalings
  {"min", val(60, s)},
  {"km",  val(1E+3, m)},
  //...

  //Derived Units (Examples)
  {"J",   val(1, kg*(m^2)/(s^2))},    //Joule   (Energy)
  //...

  //Physical Constants
  {"R",   val(8.31446261815324, kg*(m^2)/(s^2)/K/mol)},
  //...

  //Mathematical Constants
  {"pi",  val(3.14159265359, D)},
  //...

};

//Extract Value
val getval(string s){
  auto search = ud.find(s);
  if(search != ud.end()){
    val m = ud[s];
    return m;
  }

  cout<<"Could not identify unit \""<<s<<"\""<<endl;
  exit(0);
}

Если задать, что некоторые величины являются безразмерными, то можно включить в таблицу поиска и математические константы.

Примечание: скомбинированные единицы обычно представляются неким «ключом» или строкой, которые люди могут понимать по-разному. В отличие от них, таблицу поиска легко модифицировать!

Примечание: оператор ^ в таблице поиска требует заключения в скобки из-за его низкого порядка предшествования.

Парсинг выражений


Для своего калькулятора я задал пять компонентов выражения: числа, единицы, операторы, скобки и особые символы.

Каждый символ в допустимом выражении можно отнести к одной из этих категорий. Следовательно, первым шагом будет определение того, к какому классу принадлежит каждый символ, и сохранение его в виде, включающем в себя эту информацию.

Примечание: «особые» символы обозначают унарные операторы, преобразующие значение. Примеры кода написаны на C++ и используют стандартную библиотеку шаблонов.

Мы зададим «класс парсинга» при помощи простого нумератора и зададим «кортеж парсинга» как пару между символом и его классом парсинга. Строка парсится в «вектор парсинга», содержащий упорядоченные кортежи парсинга.

enum pc {                         //Parse Class
  NUM, UNT, OPR, BRC, SPC
};

using pt = std::pair<pc,char>;    //Parse Tuple

using pv = std::vector<pt>;       //Parse Vector

Мы создаём вектор парсинга, просто сравнивая каждый символ со множеством символов, содержащихся в каждом классе.

// Error Handling

void unrecognized(int i, char c){

  cout<<"Unrecognized character \""<<c<<"\" at position "<<i<<endl;

  exit(0);

}

// Construct a parse vector from a string!

pv parse(string e){

  pv parsevec;

  // Iterate over the string

  for(string::size_type i = 0; i < e.size(); i++){

    const char c = e[i]; // Get the next character

    // Permissible characters for each class

    string brackets = "[]";
    string operators = "+-*/^%";    //Binary Operators
    string special = "!~E";         //Unary Operators
    string numbers = "0123456789.";

    // Identify the class and add a parse tuple to the vector

    if(numbers.find(c) != string::npos)
      parsevec.push_back(pt(NUM, c));

    else if(isalpha(c))
      parsevec.push_back(pt(UNT, c));

    else if(operators.find(c) != string::npos)
      parsevec.push_back(pt(OPR, c));

    else if(brackets.find(c) != string::npos)
      parsevec.push_back(pt(BRC, c));

    else if(special.find(c) != string::npos)
      parsevec.push_back(pt(SPC, c));

    else unrecognized(i, c);

  }

  return parsevec;

}

Структура нашей основной программы заключается в сжатии выражения, построении вектора парсинга и передаче его в вычислитель, возвращающий вычисленное выражение:

// MAIN FILE

using namespace std;

// ...

// Compress the command line input
string compress(int ac, char* as[]){
  string t;
  for(int i = 1; i < ac; i++)
    t += as[i]; // append to string
  return t;
}   // Note that spaces are automatically sliced out

// Compress, Parse, Evaluate
int main( int argc, char* args[] ) {

  string expression = compress(argc, args);
  pv parsevec = parse(expression);

  val n = eval(parsevec, 0);
  cout<<n<<endl;

  return 0;

}

Для нашего примера выражения это будет выглядеть так:


Распарсенный пример выражения. Каждый символ в строке может быть отнесён к конкретной категории. Числа обозначены красным, единицы оранжевым, операторы синим, скобки фиолетовым, а особые символы — зелёным.

С самым лёгким мы закончили. Создан вектор парсинга из входящих данных командной строки и теперь мы можем оперировать с числами, связанными со значениями.

Как вычислить вектор парсинга, чтобы получить единичное значение?

Вычисление выражений


Нам осталось вычислить вектор парсинга, для чего требуется информация о структуре семантических математических выражений.

Здесь можно сделать следующие важные наблюдения:

  1. Связанные друг с другом числа и единицы в выражении всегда находятся рядом
  2. Унарные операторы можно применять напрямую к связанным с ними парами «число-единица»
  3. Двоичные операторы используются между парами «число-единица», возвращая одну новую пару «число-единица»
  4. Двоичные операторы имеют определённый порядок вычислений
  5. Скобки содержат выражения, которые сами по себе можно вычислить для получения пары «число-единица»
  6. Сбалансированное выражение без унарных операторов или скобок всегда состоит из N значений и N-1 операторов

После создания пар «число-единица» и применения унарных операторов вектор парсинга преобразуется в сбалансированную последовательность значений и операторов.

Одновременно внутри рекурсивным образом вычисляются скобки, чтобы свести их к одному значению.

В общем случае это означает, что вектор парсинга можно вычислить при помощи рекурсивной функции, возвращающей пару «число-единица».

Рекурсивная функция вычисления вектора парсинга


Рекурсивная функция eval описывается следующим процессом:

  1. Итеративно обходим вектор парсинга
    1. Когда встречаем скобку, вызываем eval для внутреннего выражения, чтобы получить значение
    2. Извлекаем пары «число-единица», применяя унарные операции, и сохраняем в вектор
    3. Извлекаем бинарные операции и сохраняем в вектор
  2. Применяем двоичные операторы в правильном порядке, используя наши сбаланированные векторы значений и операторов


Создание упорядоченной последовательности значений и операторов


Начнём с определения функции eval, получающей дополнительный параметр n, обозначающий начальную точку:

val eval(pv pvec, int n){

  if(pvec.empty()) return val(1.0, D);
  if(pvec[0].first == OPR) invalid(n);

  vector<val> vvec;   //Value Sequence Vector
  vector<char> ovec;  //Binary Operator Sequence Vector

  // ...

Примечание: пустой вектор парсинга возвращает безразмерное единичное значение и вектор парсинга не может начинаться с оператора.

Мы итеративно проходим по строке, отслеживая начальную и конечную точку текущей наблюдаемой последовательности. Когда мы встречаем скобку, то находим конечную точку скобки и вызываем функцию вычисления для внутреннего выражения:

  // ...

  size_t i = 0, j = 0;  //Parse section start and end
  while(j < pvec.size()){

    //Bracketing
    if(pvec[j].second == '['){

      i = ++j;  //Start after bracket
      for(int nbrackets = 0; j < pvec.size(); j++){
        if(pvec[j].second == '[') //Open Bracket
          nbrackets++;
        else if(pvec[j].second == ']'){
          if(nbrackets == 0) //Successful close
            break;
          nbrackets--; //Decrement open brackets
        }
      }

      //Open Bracket at End
      if(j == pvec.size())
        invalid(n+i-1);

      //Recursive sub-vector evaluate
      pv newvec(pvec.begin()+i, pvec.begin()+j);
      vvec.push_back(eval(newvec, n+j));
    }

    // ...

Это приведёт к рекурсии, пока не будет найдено выражение вектора парсинга, не содержащее скобок, а значит, состоящее из сбалансированной последовательности значений и операторов.


При вычислении внутреннего выражения скобки возвращается некое значение. После уничтожения всех скобок останется только сбалансированная последовательность значений и операторов.

Операторы можно добавлять напрямую, а значения задаются комбинацией чисел, единиц и унарных операторов. Мы можем создать значение, найдя последовательность идущих друг за другом кортежей парсинга, представляющих её, и построив его соответствующим образом:

    // ...

    //Add Operator
    if(pvec[j].first == OPR)
      ovec.push_back(pvec[j].second);

    //Add Value
    if(pvec[j].first == NUM ||
       pvec[j].first == UNT ||
       pvec[j].first == SPC ){

      i = j; //Start at position j
      while(pvec[j].first != OPR &&
            pvec[j].first != BRC &&
            j < pvec.size()) j++; //increment

      //Construct the value and decrease j one time
      pv newvec(pvec.begin()+i, pvec.begin()+j);
      vvec.push_back(construct(newvec, n+j));
      j--;
    }

    j++; //Increment j

    //Out-of-Place closing bracket
    if(pvec[j].second == ']')
      invalid(n+j);

  }

  // Check if sequence is balanced
  if(ovec.size() + 1 != vvec.size())
    fatal("Operator count mismatch");

  // ...

Мы конструируем значения из их последовательности кортежей парсинга, выявляя числовые компоненты, единицы и унарные операторы.

Создание пар «число-единица» и унарные операторы


Так как этот калькулятор поддерживает представление в числах с плавающей запятой, значение может состоять и из предэкспоненты, и из степени. Кроме того, обе эти величины могут иметь знак.

Знак извлекается как первый символ, за которым следует последовательность чисел. Значение извлекается при помощи stof:

val construct(pv pvec, int n){

  unit u  = D;       //Unit Initially Dimensionless
  double f = 1.0;    //Pre-Exponential Value
  double p = 1.0;    //Power
  double fsgn = 1.0; //Signs
  double psgn = 0.0;

  size_t i = 0;      //Current Index
  string s;
  bool fp = false;   //Floating Point Number?

  //First Character Negation
  if(pvec[i].second == '~'){
    fsgn = -1.0;
    i++;
  }

  //Get Numerical Elements
  while(i < pvec.size() && pvec[i].first == NUM){
    s.push_back(pvec[i].second);
    i++;
  }

  if(!s.empty()) f = stof(s);   //Extract Value
  s.clear();                    //Clear String

  //...

Примечание: унарный оператор, обозначающий смену знака, например, -1, представлен здесь в виде тильды (~), потому что так проще отличать его от бинарного оператора вычитания.

Далее мы проверяем наличие записи с плавающей запятой и повторяем это, чтобы получить знак и величину степени:

  //...

  //Test for Floating Point
  if(pvec[i].second == 'E'){
    i++;
    psgn = 1.0;

    if(pvec[i].second == '~'){
      psgn = -1.0;
      i++;
    }

    while(i < pvec.size() && pvec[i].first == NUM){ //Get Number
      s.push_back(pvec[i].second);
      i++;
    }
    if(!s.empty()) p = stof(s);
    else fatal("Missing exponent in floating point representation.");
    s.clear();
  }

  //Double floating point attempt
  if(pvec[i].second == 'E')
    invalid(n+i);

  //...

Наконец, мы извлекаем оставшуюся единицу как строку и получаем соответствующее значение. Применяем оставшиеся в конце унарные операторы и возвращаем окончательный вид значения:

  //...

  //Get Unit String
  while(i < pvec.size() && pvec[i].first == UNT){
    s.push_back(pvec[i].second);
    i++;
  }

  if(!s.empty()){
    val m = getval(s);
    f *= m.n; //Scale f by m.n
    u = m.u;  //Set the unit
  }

  if(pvec[i].second == '!'){
    f = fac(f);
    i++;
  }

  if(i != pvec.size())  //Trailing characters
    invalid(n+i);

  return val(fsgn*f*pow(10,psgn*p), u);
}

Этот процесс сводит все комбинации унарных операторов, чисел и единиц к структурам значений, с которыми можно оперировать при помощи бинарных операторов:


Здесь вы видите, как выражение с унарным оператором сводится к значению.

Примечание: позиция передаётся функции создания, чтобы была известна абсолютная позиция в выражении для обработки ошибок.

Сжатие упорядоченной последовательности значений и операторов


Наконец, у нас получилась сбалансированная последовательность значений и бинарных операторов, которую мы можем сжать, используя правильный порядок операций. Два значения, связанные стоящим между ними оператором, можно сжать при помощи простой функции:

val eval(val a, val b, char op){
  if(op == '+') a = a + b;
  else if(op == '-') a = a - b;
  else if(op == '*') a = a * b;
  else if(op == '/') a = a / b;
  else if(op == '^') a = a ^ b;
  else if(op == '%') a = a % b;
  else{
    std::cout<<"Operator "<<op<<" not recognized"<<std::endl;
    exit(0);
  }
  return a;
}

Чтобы сжать всю сбалансированную последовательность, мы итеративно обходим вектор парсинга по разу для каждого типа оператора в правильном порядке и выполняем бинарные вычисления. Стоит заметить, что умножение и деление могут происходить одновременно, как и сложение с вычитанием.

  //...

  function<void(string)> operate = [&](string op){
    for(size_t i = 0; i < ovec.size();){
      if(op.find(ovec[i]) != string::npos){
        vvec[i] = eval(vvec[i], vvec[i+1], ovec[i]);
        ovec.erase(ovec.begin()+i);
        vvec.erase(vvec.begin()+i+1, vvec.begin()+i+2);
      }
      else i++;
    }
  };

  operate("%");
  operate("^");
  operate("*/");
  operate("+-");

  return vvec[0];
}

Получаем окончательный результат по нулевому индексу и возвращаем его.


Скобки вычисляются рекурсивно, как внутренне сбалансированная последовательность значений и операторов. После устранения всех скобок из основного выражения возвращается окончательное значение.

Примечание: эта рекурсивная структура отражает древовидную природу семантики математического выражения.

Результаты и выводы


Описанная выше структура была обёрнута в простой инструмент командной строки, который я назвал «dima» (сокращённо от «dimensional analysis»). Полный исходный код можно найти здесь.

Этот простой калькулятор командной строки будет правильно вычислять выражения с единицами измерения.

Единицы правильно комбинируются и раскладываются:

 dima J
1 kg m^2 s^-2
> dima J / N
1 m
> dima J/N + 2cm
1.02 m

одновременно позволяя быстро узнавать значения констант:

> dima R
8.31446 kg m^2 K^-1 mol^-1 s^-2

При необходимости таблицу поиска выражений с единицами можно модифицировать.

Можно расширить эту систему, добавив способ задания функций/преобразований с именами.

Ещё одно потенциальное улучшение: можно добавить некий буфер вычислений, при помощи оператора присваивания сохраняющий переменные в новом словаре, доступ к которому можно получить при других последующих вычислениях. Однако для такого сохранения состояния потребуется запись в файл или запуск процесса.

Этот семантический математический парсер можно полностью преобразовать и создать другие полезные математические программы.

Например, можно попробовать алгебраически преобразовывать выражения с переменными, чтобы находить более изящное представление на основании какого-нибудь способа оценки (длины, симметрии, повторяющихся выражений и т.д.)

Ещё одной возможной вариацией может стать вспомогательная функция дифференцирования, использующая алгоритмическую природу производных.


На правах рекламы


Наша компания предлагает виртуальные серверы в аренду для любых задач и проектов, будь то серьёзные выслечения или просто размещение блога на Wordpress. Создавайте собственный тарифный план в пару кликов и за минуту получайте готовый сервер, максимальная конфигурация бьёт рекорды — 128 ядер CPU, 512 ГБ RAM, 4000 ГБ NVMe!