12.03.2021 08:09
PatientZero 18 5600 Источник
image

«В гудении струн есть геометрия, в расположении сфер есть музыка» — Пифагор

В детстве у меня была игрушка под названием «спирограф», которая досталась мне в наследство от родителей. Я любил её. Она генерировала сложные узоры и шаблоны, многократно повторявшиеся по кругу. Для восьмилетнего меня это было настоящее волшебство.


Рисовать им было очень просто — вставляешь зубчатое колесо с несколькими отверстиями внутрь ещё одного зубчатого кольца побольше, в одно из отверстий засовываешь конец ручки и рисуешь узоры.


Спустя 20 лет мои инструменты немного изменились, но, тем не менее, любовь к сложным узорам никуда не делась. Да, я нашёл новые способы изучения этих узоров, и меня не перестаёт удивлять то, что я могу делать и куда меня может завести воображение. Обычно для генерации красивых изображений я пользуюсь библиотекой Processing (упрощённой формой Java), созданной Processing Foundation (примеры можно найти здесь). Существуют и другие способы, например, OpenFrameworks, Nannou и Cinder.

Но на этот раз я решил использовать нечто совершенно иное. Всё началось с того, как я занимался по учебнику статистики и снова познакомился с параметрическими уравнениями (представлениями). Я стал исследовать их, запуская уравнения в Excel и выводя их на графики, чтобы убедиться в правильности значений и получить интуитивное понимание таких уравнений.


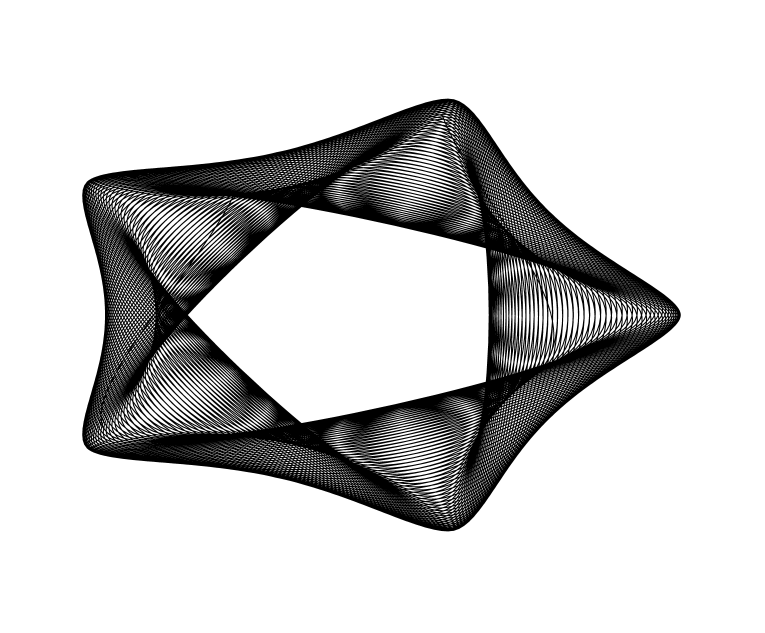
a = 10; b = 2

Параметрические представления


Если объяснять просто, то параметрическое уравнение (представление) — это ещё один способ выражения функции. Обычно они используются в задачах или уравнениях кинематики (задачах основ физики) для описания таких свойств, как траектория ракеты или орбита планеты, вращающейся вокруг массивного объекта.

Давайте рассмотрим следующую функцию, которая создаёт параболу.


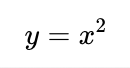
График параболы (y = x?)

Чтобы получить эту функцию, мы можем разложить (при помощи вузовской алгебры) вышеприведённое уравнение, изолировав X и Y и сгенерировав отдельный параметр, входящими данными которого является t, как показано в функции ниже.



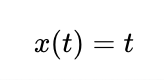
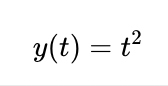
Две параметрические функции параболы

По сути, если мы создадим таблицу этих двух интерпретаций функции, то они будут давать одинаковые ответы.



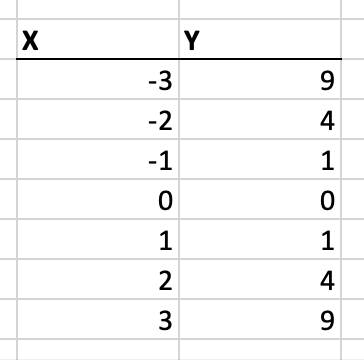
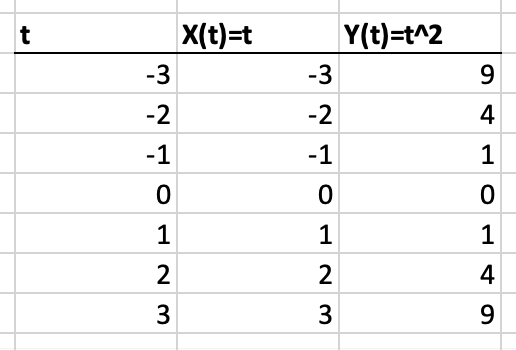
Обычная функция (сверху) и параметрическая функция (снизу)

Всё довольно легко, правда?

По сути, когда мы используем две функции для генерирования координат X и Y, то можем, как вы увидите ниже, создать огромное количество графики, примеры которой представлены в этом посте. (Помните, что это всего один набор уравнений).



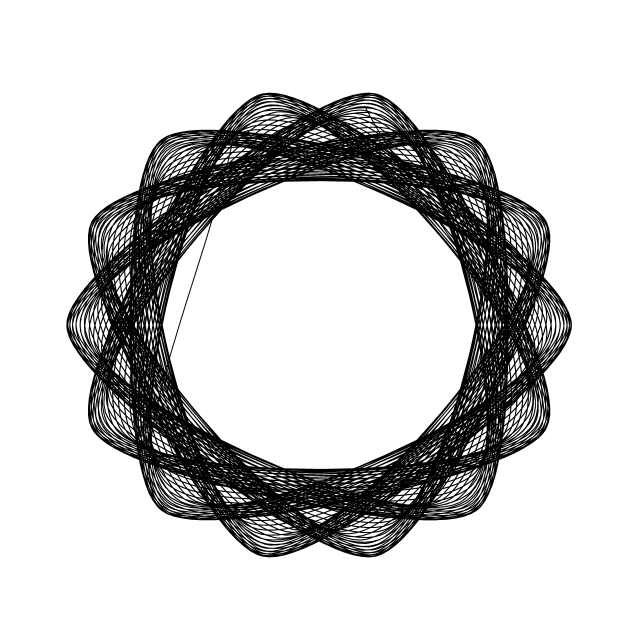
a = 23; b = 2



a=5; b=30




a=5; b=2.51

А теперь самое интересное — ниже я опишу процесс, благодаря которому сгенерировал все представленные в посте изображения.

Как творить в Excel


1. Откройте новую таблицу и создайте на листе следующее.


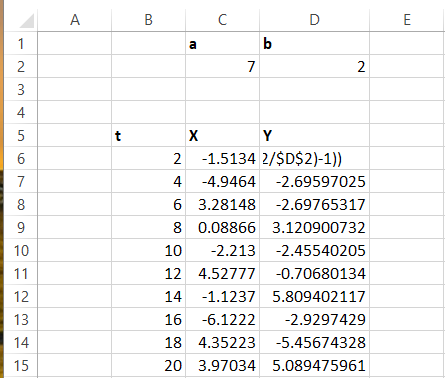
2. Под всеми изображениями я добавил коэффициенты a, b и растянул вниз листа значения (2 ? t ? 2000).

3. Для X используйте следующую формулу, начинающуюся в C6

=($C$2-$D$2)*COS(B6)+$D$2*COS(B6*(($C$2/$D$2)-1))

4. Для Y используйте следующую формулу, начинающуюся в D6

=($C$2-$D$2)*SIN(B6)-$D$2*SIN(B6*(($C$2/$D$2)-1))

5. Растяните вниз все формулы, чтобы X и Y были заполнены значениями до t=2000 и выделите X и Y.

6. Перейдите на вкладку «Главная», выберите «Диаграмма рассеяния» (scatterplot) и нажмите «Точечная (XY) с гладкими линиями».


Обратите внимание, что можно менять тип диаграммы и что он выглядит примерно так:


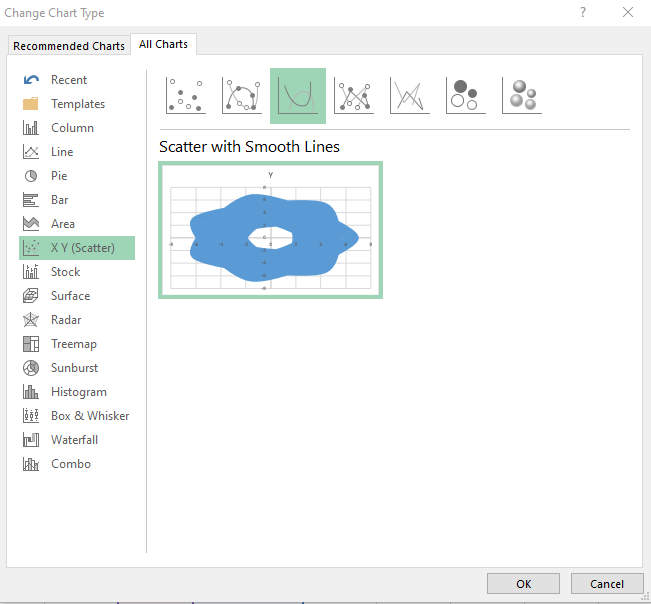
7. Теперь удалим оси X и Y и изменим размер изображения таким образом, чтобы оно выглядело интересно.


Так вы получите изображение, которое затем можно будет экспортировать как графический файл. Теперь можно поэкспериментировать с ним, меняя коэффициенты и наблюдая за различными создаваемыми структурами параметрического изображения. Кроме того, можно изменить цвет фона и изображения, выбрав изменяемый компонент изображения и использовав инструменты форматирования, после чего выбрав форму и контур фигуры.


Или можно скачать готовую таблицу Excel с Dropbox.


Чтобы добавить текст, используйте любой графический редактор или даже сам Excel, после чего можно или сделать скриншот, или экспортировать изображение, а затем использовать его в своих графических работах.



a=5; b=1

Ссылки