
Функциональное программирование может отпугивать сложностью и непрактичностью: «Я далек от всех этих монад, пишу на обычном C#, в докладе про функциональщину ничего не пойму. А если даже напрягусь и пойму, где мне потом это применять?»
Но когда объясняет Скотт Влашин, все совершенно не так: его доклад о композиции с конференции DotNext 2019 Moscow — пример того, как можно доносить функциональные идеи простыми словами. Он за час перешел от бананов к монадам так, что второе кажется немногим сложнее первого. А в конце объяснил, почему осмыслить композицию полезно даже тем, кто не собирается покидать мир ООП. Примеры кода в докладе как на F#, так и на C#.
Уже завтра начнется новый DotNext, где я помогу Скотту выступить с другим докладом, а пока что публикую перевод его выступления про композицию. Далее повествование будет от лица Скотта.
Оглавление
- Философия композиции
- Идеи функционального программирования
— Функции и их композиция
— Типы и их композиция - Композиция на практике
— Римские цифры
— Нетипичный FizzBuzz
— Охохонюшки, монады!
— Веб-сервис - Итоги
Философия композиции
Чтобы понять композицию, необходимо обладать некоторым опытом:
- Вы должны были быть ребенком.
- У вас должен быть опыт игры в Lego.
- И опыт с игрушечной железной дорогой.
Поскольку ребенком был каждый, с первым пунктом сразу порядок. Теперь давайте поговорим про Lego.
Философия Lego

- Все детали предназначены для соединения с другими деталями. На них есть маленькие «кнопочки», позволяющие их соединять.
- Детали можно переиспользовать в разных контекстах. Из одних и тех же деталей можно построить совершенно разные вещи. И, что очень важно, каждая деталь самодостаточна: чтобы она выполняла свою функцию, не требуется электричество или какие-то другие детали.
- Если соединить две детали Lego, то вы получите «новую деталь Lego», которую можно снова соединить с другой деталью, и так до бесконечности. Если собирать детали достаточно долго, можно в итоге получить очень большие фигуры.
Как, например, эта:

И даже на ней все еще есть кнопочки, и мы можем продолжить строить и строить.
Это я и называю силой композиции.
Философия игрушечной железной дороги
Здесь все то же самое:
- Все детали предназначены для соединения с другими.
- Каждую можно использовать для разных дорог.
- Если соединить две детали, то мы получим деталь побольше, которую опять можем использовать и строить дороги все длиннее и длиннее.

Eсли вы понимаете, как работают Lego и игрушечная железная дорога, то, в принципе, вы понимаете все про композицию, можно расходиться!
Идеи функционального программирования

1. Функция — это сущность
Функции — это не методы, это сущности. Функцию можно рассматривать как кусочек железной дороги с туннелем. Я называю его «туннель трансформации», потому что заезжает в него одна сущность, а выезжает другая. Вот функция, преобразующая яблоки в бананы:
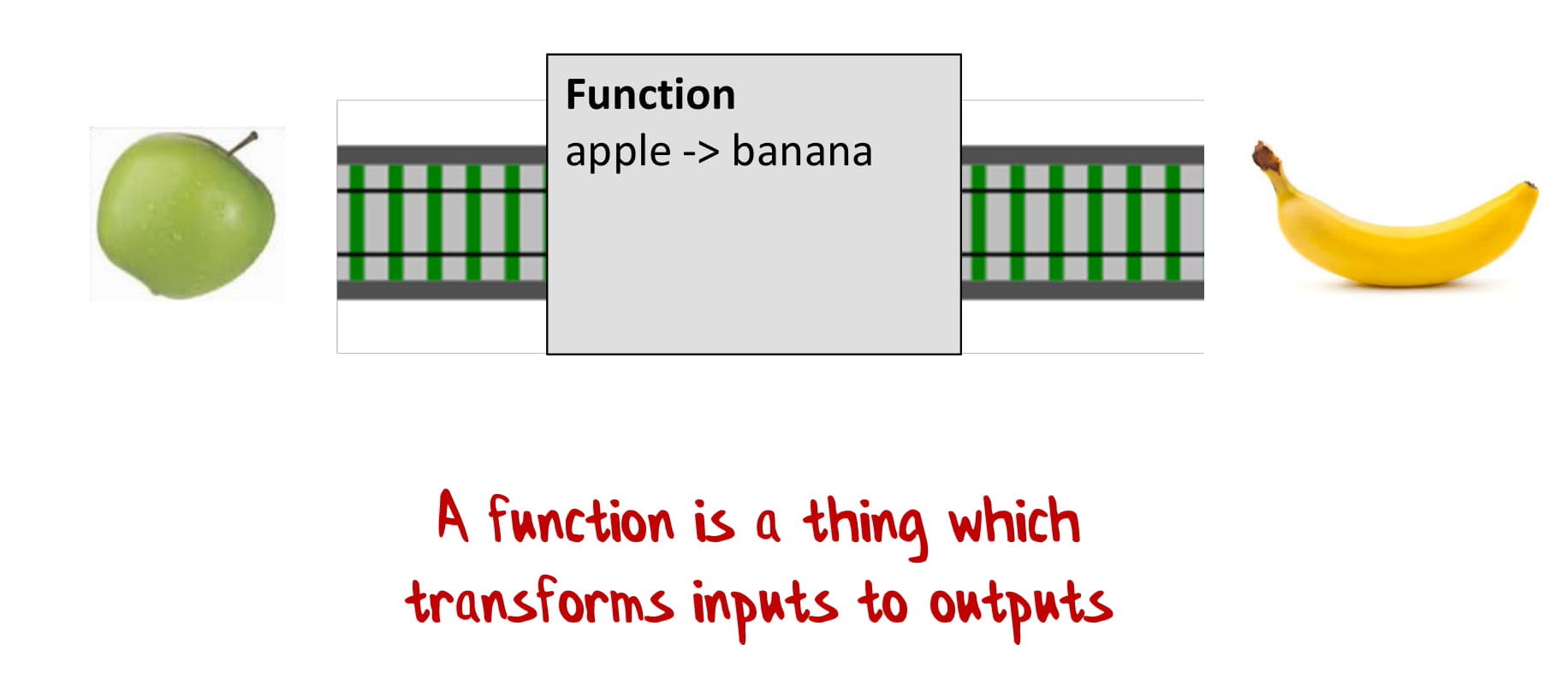
Важно понять, что это автономная единица, а не метод, который привязан к классу. «Автономная» можно понимать как «повторно-используемая». Это сущность, которую можно использовать как и другие сущности — int, String или DateTime.
Функция может быть использована как входное значение для другой функции или быть результатом ее выполнения: везде, где вы можете использовать int или String, можете использовать и функцию.
Рассмотрим примеры четырёх ситуаций.
Функция как результат выполнения функции:

Функция как входное значение:

Функция как параметр:
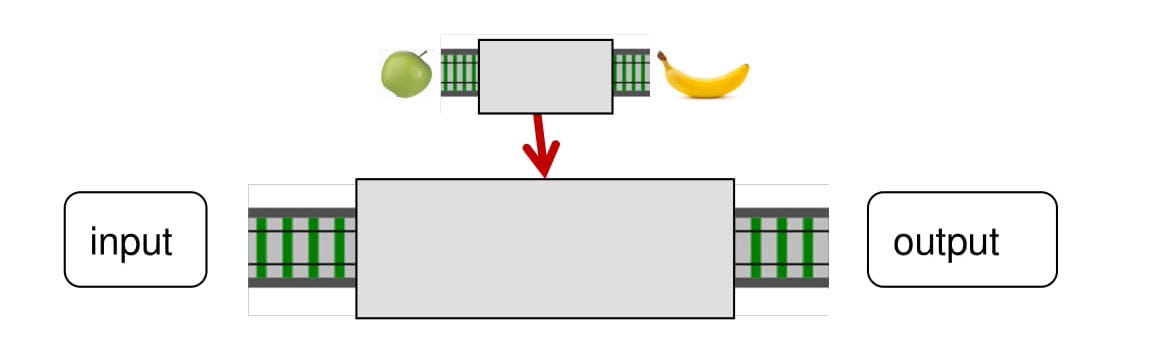
Функция как входное значение и как результат выполнения:

Это и есть суть функционального программирования. Звучит довольно прямолинейно, но, конечно, на практике всё может быть непросто. У вас может быть функция, которая возвращает функцию, которая порождает функции, которые используют функции как параметр. Но идея за всем этим стоит всё та же.
2. Композиция позволяет «строить» более крупные функции
Давайте попробуем создать одну функцию из двух других. Как нам их соединить?
Тут вполне очевидно, мы возьмем результат первой функции и передадим его второй функции:
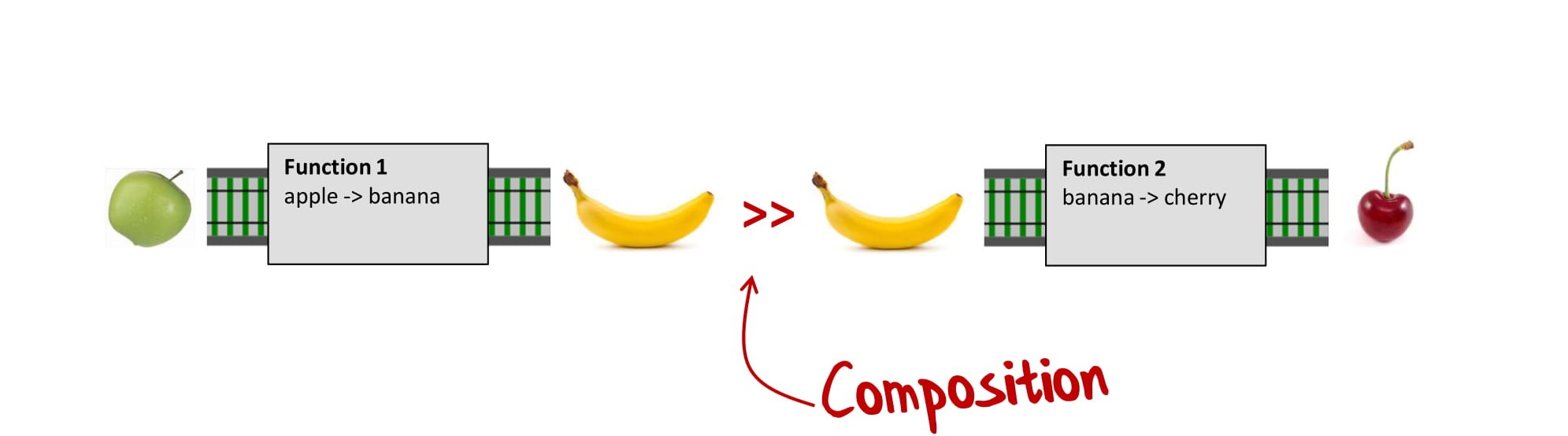
И тогда мы получим новую функцию, которая преобразует яблоки в вишни. И что важно, вы не видите, что на самом деле новая функция — это композиция двух других функций:
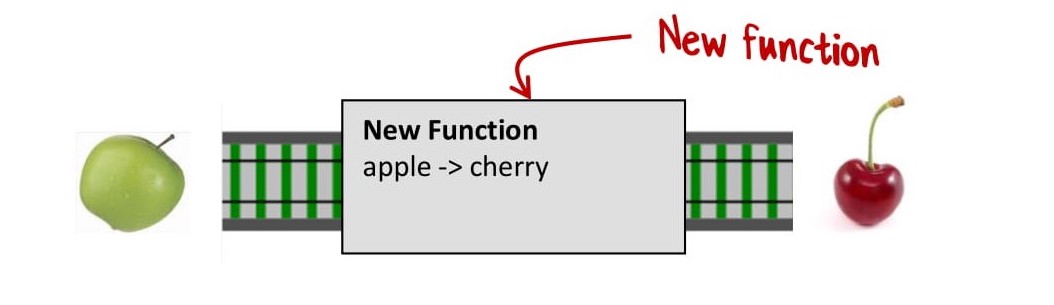
Но куда же делся банан?
Дело в том, что мы перешли на другой уровень абстракции. Нижний уровень разбирается с бананами, чтобы верхнему уровню не приходилось о них думать.
И, конечно, вы можете взять эту функцию и продолжить составлять с ее помощью все новые и новые функции.
Давайте посмотрим, как это можно сделать на C# и F#. Возьмем три метода на С#:
int add1(int x) => x + 1;
int times2(int x) => x * 2;
int square(int x) => x * x;А затем к 5 прибавим 1 (add1), умножим на 2 (times2) и возведем все в квадрат (square).
add1(5);
times2(add1(5));
square(times2(add1(5)));При обычном подходе мы получаем множество скобочек. Чтобы разобраться, что к чему, придется найти самую вложенную функцию посередине и затем «прорываться наружу» через все эти скобочки, просматривая функцию за функцией. И порой это сложно.
Функциональный подход заключается в создании «пайплайнов» или конвейеров. Если вы знаете о UNIX pipes, то это то же самое.
Мы берем 5 и «скармливаем» ее функции add1. Потом берем результат и передаем в функцию times2. Затем, то, что получилось, передаем в square и получаем 144.

Мы как бы соединяем эти функции и пропускаем данные через них. И часто это намного понятнее, особенно когда вы пишете что-то очень сложное и большое.
Как сделать такой пайплайн на F#? Там у нас есть специальный оператор |> (аналог оператора | в UNIX), который означает «взять результат и скормить его дальше»:
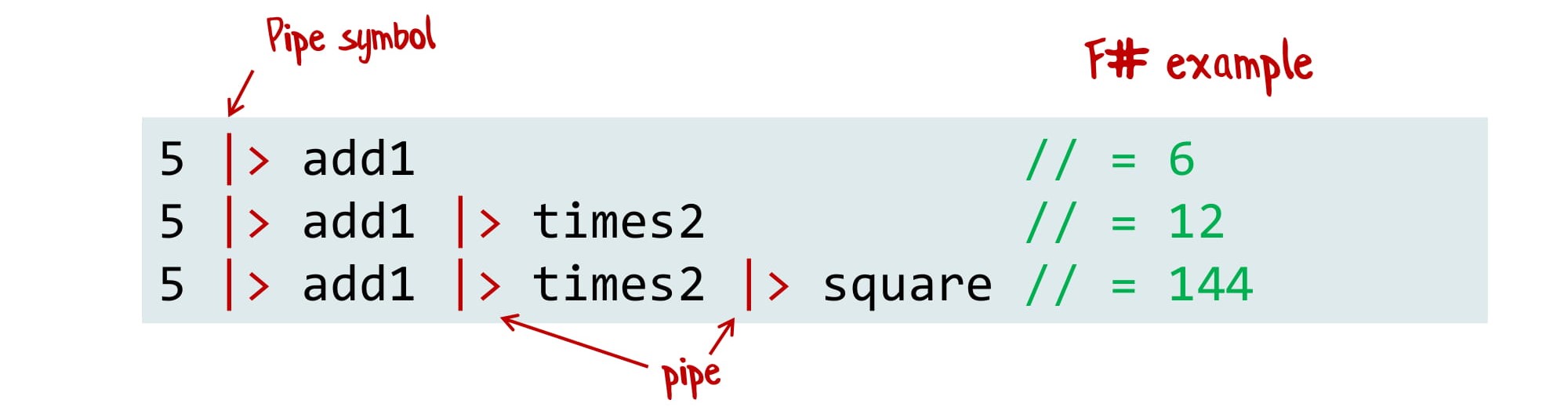
В F# этот оператор встречаешь на каждом шагу. В C# такого нет, однако мы можем написать extension method, работающий с любым объектом:

Может выглядеть странновато, но смотрите на это как на UNIX-пайплайны.
Теперь поговорим о составлении больших систем из функций.
Допустим, у вас есть низкоуровневая операция. Например, функция ToUpper(), которая переводит строку в верхний регистр.

И вы берете несколько низкоуровневых операций и соединяете их в сервис. Например, сервис, валидирующий адрес. Он принимает адрес, а выдает результат валидации.
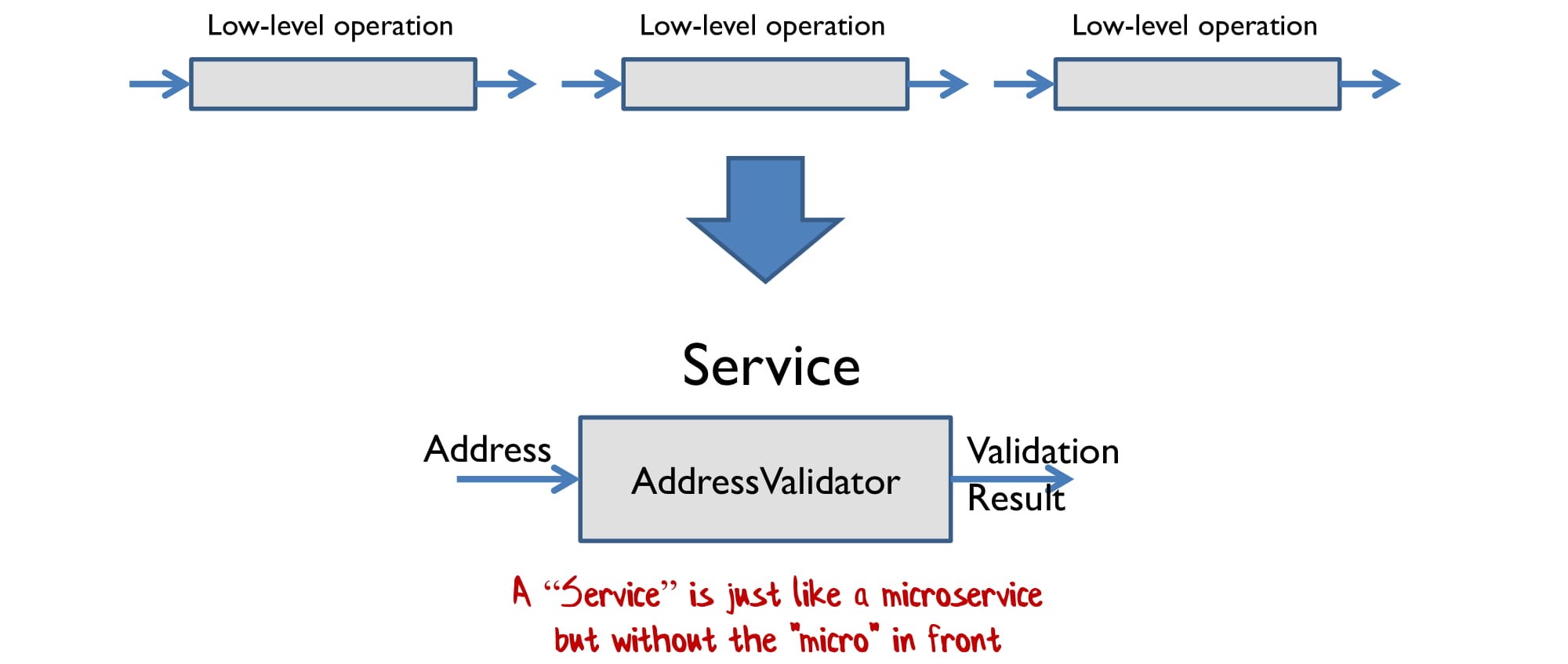
Я называю это словом «сервис», потому что мне уже за сорок. Если вы младше, можете говорить «микросервис».
А дальше возьмем несколько сервисов, соединим вместе, и появляется уже определенный пользовательский сценарий. Например, обновление данных профиля.
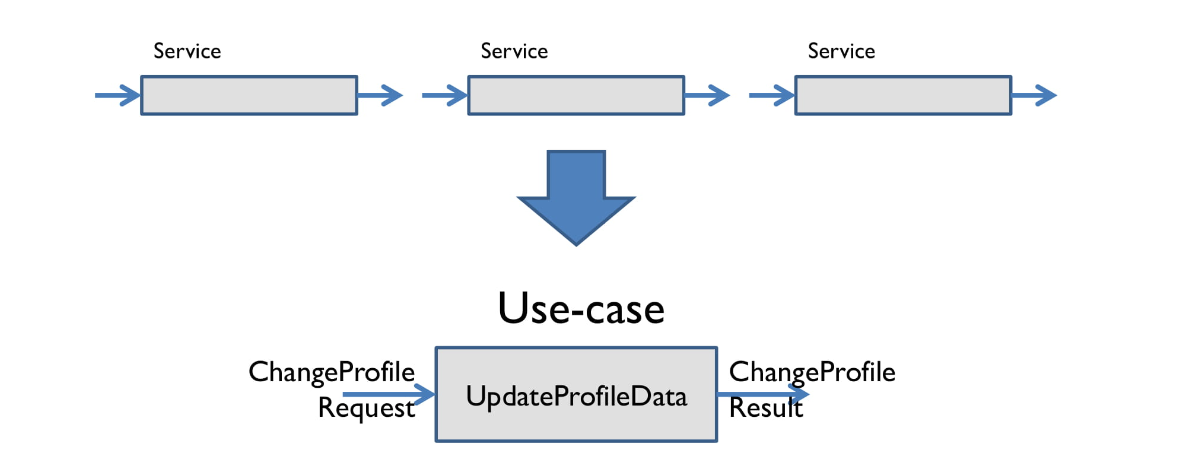
А теперь поговорим о целом веб-приложении. Если вдуматься, то веб-приложение — это функция. Её входное значение — это HttpRequest, а результат — HttpResponse.
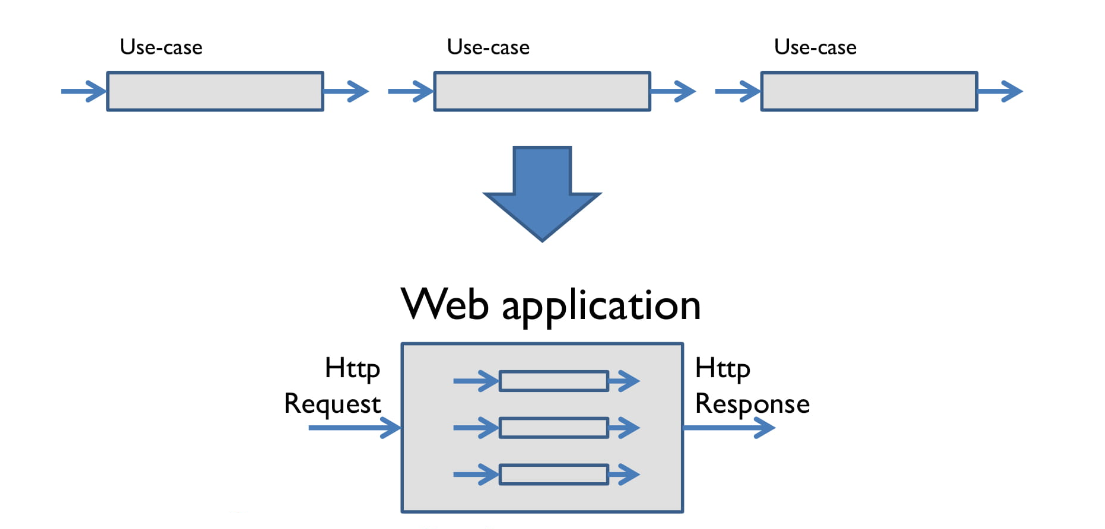
И внутри этой большой функции вам просто нужно решить, какую из функций поменьше (какой пользовательский сценарий) вам надо вызвать.
Как можно заметить, мы используем один и тот же подход на всех уровнях. Композиция везде работает одинаково.
Вот что мы увидим, заглянув внутрь веб-приложения. Есть функции поменьше, и, конечно, есть ветвление, это не просто единый пайплайн с начала до конца. Но интересно, что даже в сложных приложениях данные движутся в одном направлении — без циклов и спутанных клубков. В функциональной парадигме данные почти всегда однонаправленные. И это делает всё лёгким для понимания.
3. Типы — это не классы
Все мы знаем, что такое класс в объектно-ориентированном подходе. Это набор защищенных данных с инкапсулированным поведением. Однако в функциональном программировании типы больше похожи на множества.
Давайте посмотрим на функцию. У нее есть множество значений, которые она может принять, и множество значений, которые эта функция может вернуть:
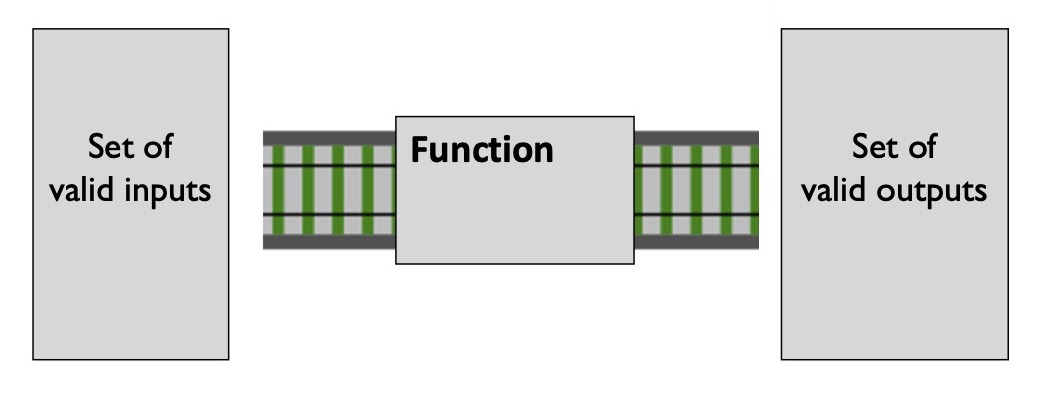
И тип — это просто название для таких множеств.
Например, мы можем сказать, что функция примет любое целое число, так что мы назовем этот тип «Integer», а вернуть может какую угодно строку, и этот тип назовем «String». Выглядит как класс, но это просто множество, там нет методов.
Из-за того что тип — это всего лишь множество, там может быть что угодно, хоть все люди в мире, хоть все существующие фрукты. И в том числе типом может быть функция:

4. Композиция позволяет «строить» более крупные типы
Из типов тоже можно составлять композиции. Раз это просто множества, то все, что мы можем сделать с множествами, мы можем делать и с типами. Можем брать объединение двух типов, пересечение, декартово произведение, потому что у типов не прописано поведение, у них нет никаких методов.
В функциональном программировании это называется алгебраической системой типов, но я называю это композиционной системой типов, потому что суть тут в композиции.
Мы можем составлять большие типы из маленьких двумя способами:
- С помощью логического «И».
- С помощью логического «ИЛИ».
Давайте рассмотрим каждый способ в отдельности.
Композиция с помощью "И". Допустим, мы хотим создать фруктовый салат. Это яблоко И банан И вишня.

И как же нам создать это в виде типа?
В С# для этого используются struct и enum:

Вместо struct можно использовать классы, но у struct нет никаких методов, поэтому это больше походит на типы.
В F# все похоже:

Заметьте, что объявление типа идет после названия переменной. В этом плане F# больше похож на JavaScript.
В мире F# мы называем полученный тип «record type».
В C# 9 тоже появились «записи».
В принципе, с этим вы уже знакомы по C#. А вот что вы не так хорошо знаете — это композиция с помощью «ИЛИ».
Допустим, я хочу перекусить, и для меня перекус — это яблоко ИЛИ банан ИЛИ вишня.

В C# нет подходящих инструментов для подобного, поэтому давайте посмотрим на F# код:
В C# 9 есть библиотеки, эмулирующие discriminated unions.

Для «ИЛИ» используется вертикальная черта.
В F# такие типы называются discriminated unions, в других языках их называют sum types, а я называю их «choice» types, потому что мы выбираем между этими вариантами.
Эти типы можно представлять себе как enum с дополнительной информацией для каждого выбора, и в C# такого сделать нельзя.
Как это может пригодиться? Давайте представим, что мы делаем платежную систему, которая принимает наличные, Paypal и банковские карты:
- Для получения наличных нам не нужна никакая дополнительная информация.
- Если оплата идет через Paypal, то нам нужен email.
- А если через карту, то нужен ее тип и номер.
То есть для каждого случая есть некоторая дополнительная информация. И как же нам это реализовать?
Если мы пишем в объектно-ориентированном подходе, то, скорее всего, мы создадим интерфейс IPaymentMethod, и после напишем 3 класса, которые реализуют этот интерфейс. И для каждой реализации нам нужны будут разные данные.

Это стандартный объектно-ориентированный подход к решению данной задачи. А теперь давайте посмотрим, как делать это с помощью композиции. В F# мы строим большие типы из маленьких.
Начнем с примитивов. Email и номер карты — это просто строки.

Затем определим тип карты. Это Visa ИЛИ MasterCard, то есть выбор, choice type.

Далее добавим информацию о карте. Это тип карты И номер карты, то есть record type.

Теперь мы можем написать наш тип оплаты. Это наличные ИЛИ PayPal ИЛИ карта. В каждом случае своя соответствующая информация — в первом случае не требуется ничего, во втором адрес, в третьем данные карты.
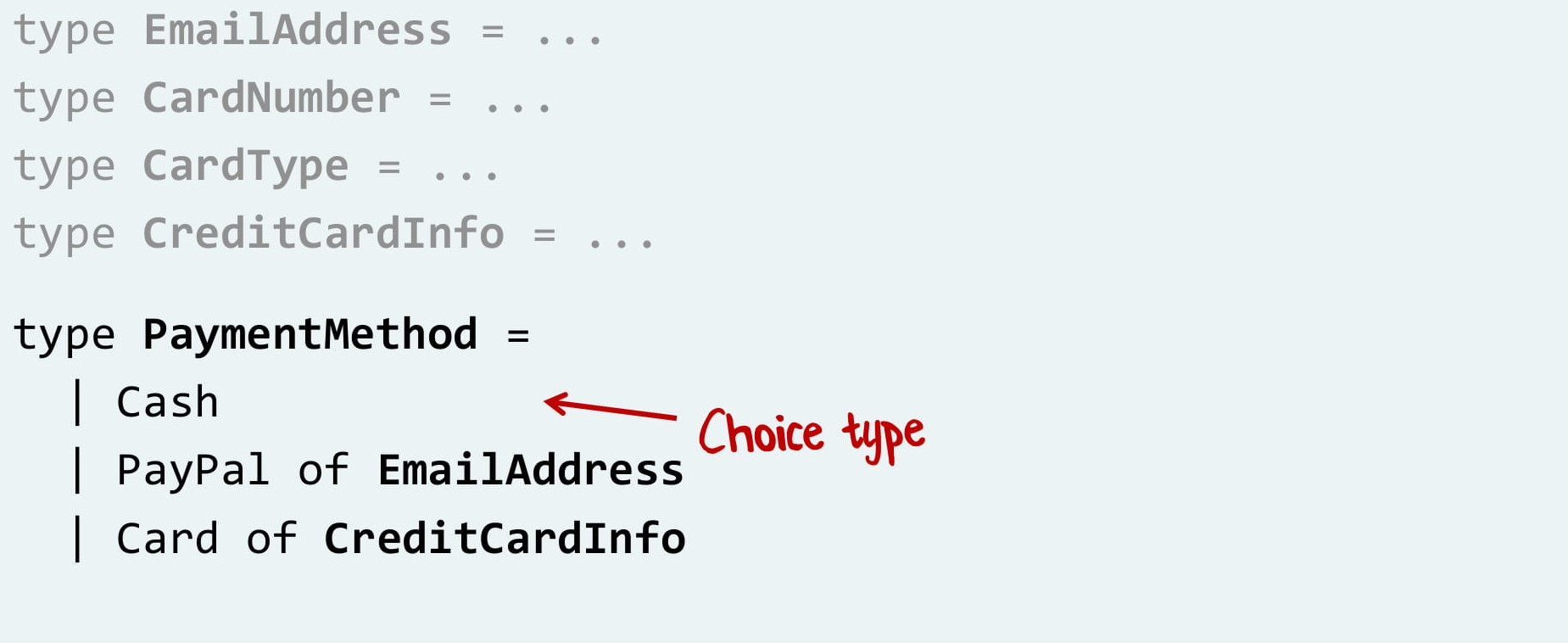
Вот так мы бы написали систему оплаты на F#. И что самое классное, мы можем и не останавливаться, совсем как в Lego. Давайте продолжим, добавим размер платежа и валюту! Размер — просто число, валюта — выбор между евро, долларом и рублем.
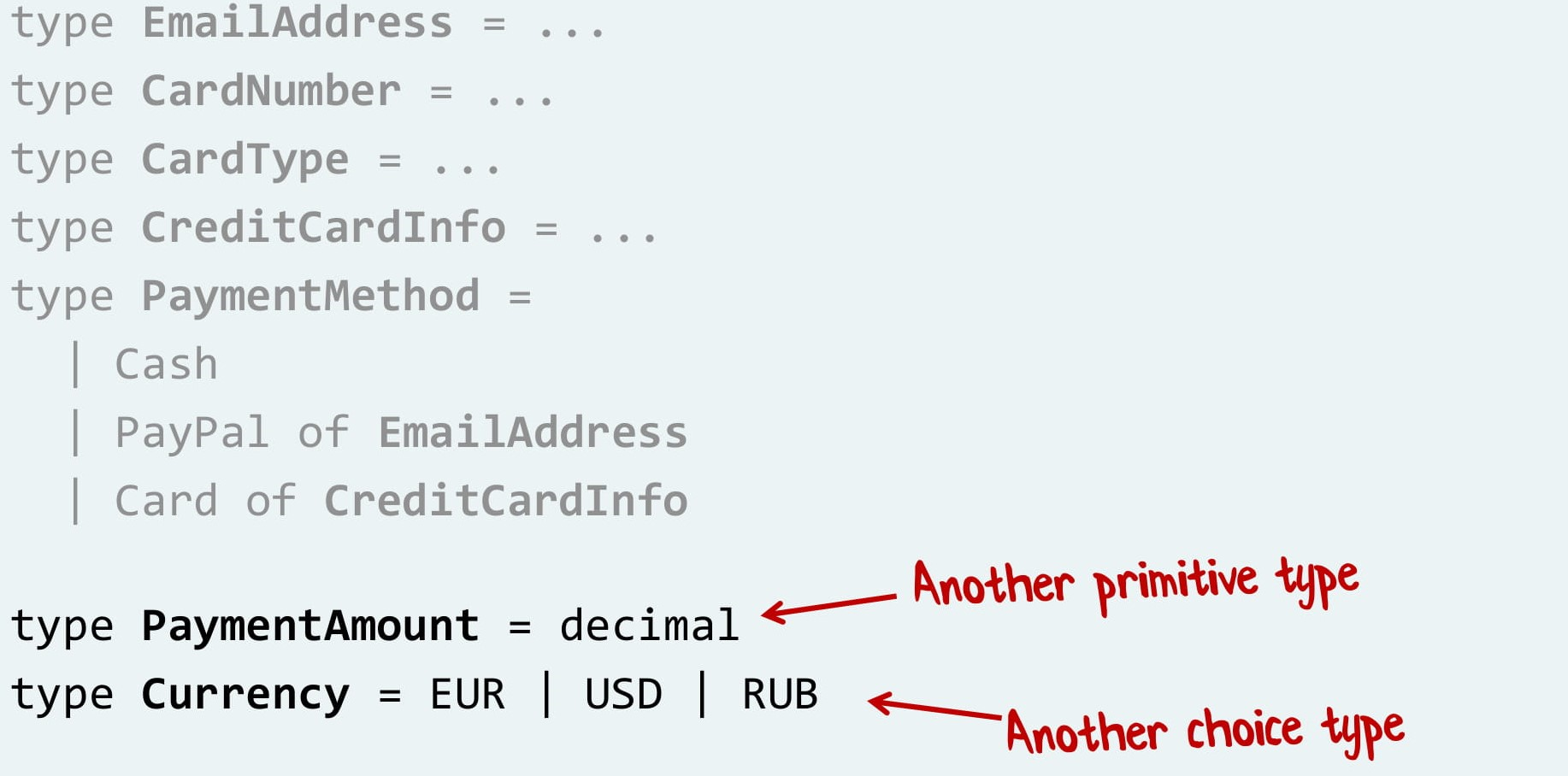
Теперь мы можем сделать тип «Платеж»: это размер платежа И валюта И тип оплаты.
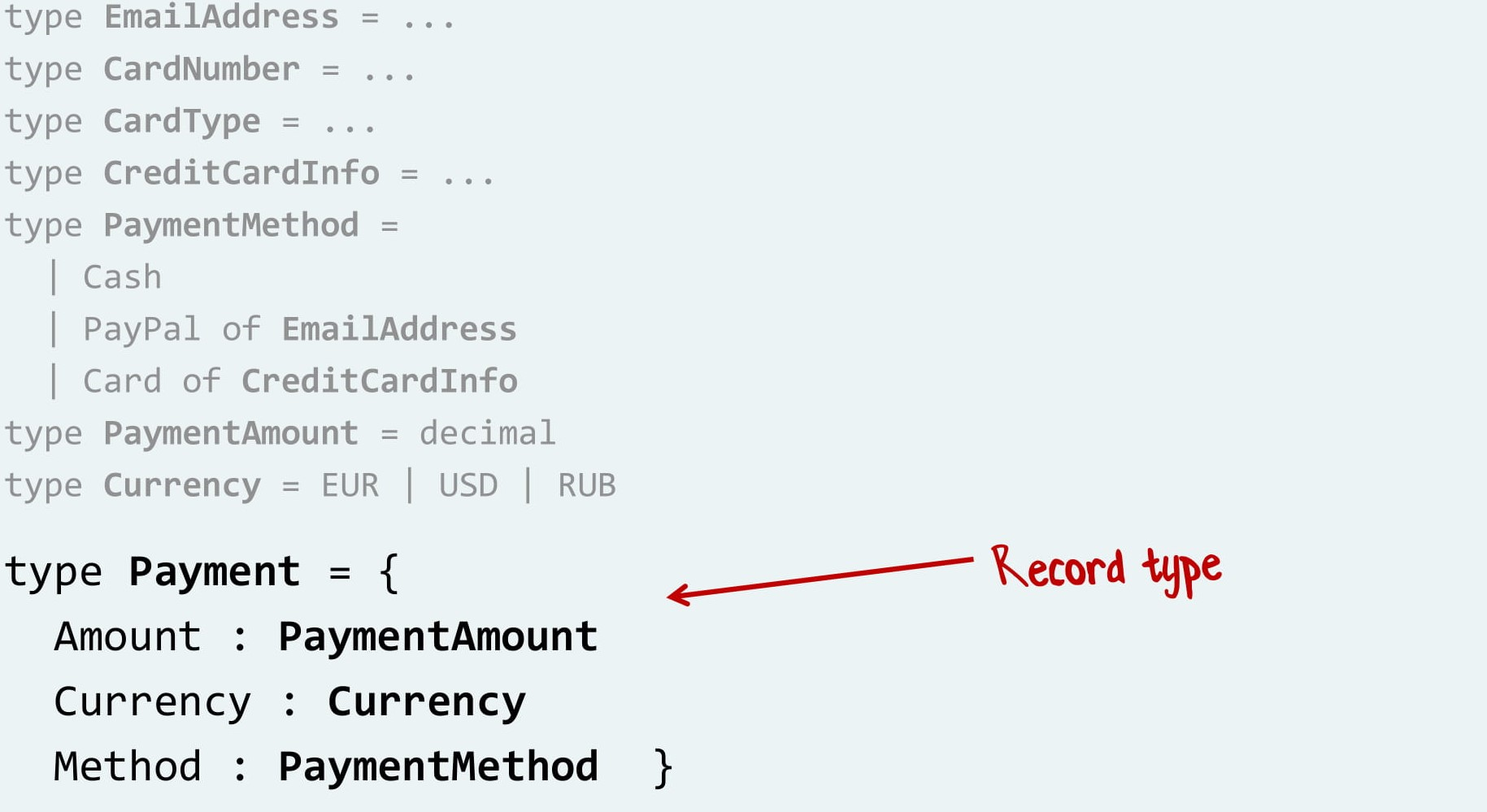
Так вместо привычного наследования мы тут растем «снизу вверх» и собираем большие типы из маленьких. Поначалу это может быть непривычно, но когда осваиваешься, очень здорово.
Отдельно хорошо, что получается понятный код, и созданные композицией типы могут служить «исполняемой документацией». Давайте убедимся в этом. Вот код, попробуйте угадать, что здесь происходит:

Думаю, вполне понятно, что это все как-то связано с карточными играми. Здесь есть «карта» (Card), «колода» (Deck) и «карты на руке» (Hand).
Но мы не ограничиваемся только существительными, мы также можем описать и глаголы. Например, если вы хотите взять карту (PickupCard), то у вас в качестве входных данных есть Hand и Card, а в результате вы получаете новый набор карт на руке Hand.
То есть мы можем смоделировать как вещи, так и действия.
И если вы работаете с людьми вроде бизнес-аналитиков, которые не разбираются в программировании, то такой код — это отличный способ взаимодействия с ними, потому что они могут читать его и указать вам на ваши ошибки.
Также такой подход облегчает жизнь новым разработчикам. Допустим, вы пришли в новую команду, и вам нужно узнать, сколько методов оплаты поддерживает приложение. Сможете ли вы понять это самостоятельно по этому коду, учитывая, что вы не читали документацию?

Да, конечно. Вам не требуется искать информацию по двадцати разным файлам, она подана очень наглядно.
На этом заканчиваем с теорией. Всё тут не перескажешь, но про Domain-Driven Design я написал целую книгу «Domain Modeling Made Functional», а на сайте об этом сделал специальный раздел.
Композиция на практике
Композиция с помощью пайплайна (на примере римских цифр)
Как перевести арабские числа в римские?

Есть разные способы решения. Мой основан на том, что римские цифры исходно отталкивались от зарубок на стенах. Когда набиралось четыре, дальше пятой их перечёркивали — думаю, оттуда и пошло «V».
Алгоритм будет следующим:
- Сначала мы n раз пишем «I», где n — это наше число на входе.
- Далее мы заменяем:
- Каждые 5 «I» на «V»
- 2 «V» на «X»
- 5 «X» на «L»
- И 2 «L» на «C»
- И так далее
По сути, это пайплайн (или конвейер). Мы сначала заменяем все «I» на «V», после берем результат и передаем следующей функции, которая заменяет «V» на «X», и так далее. Мы как бы «пропускаем» данные через эти функции.
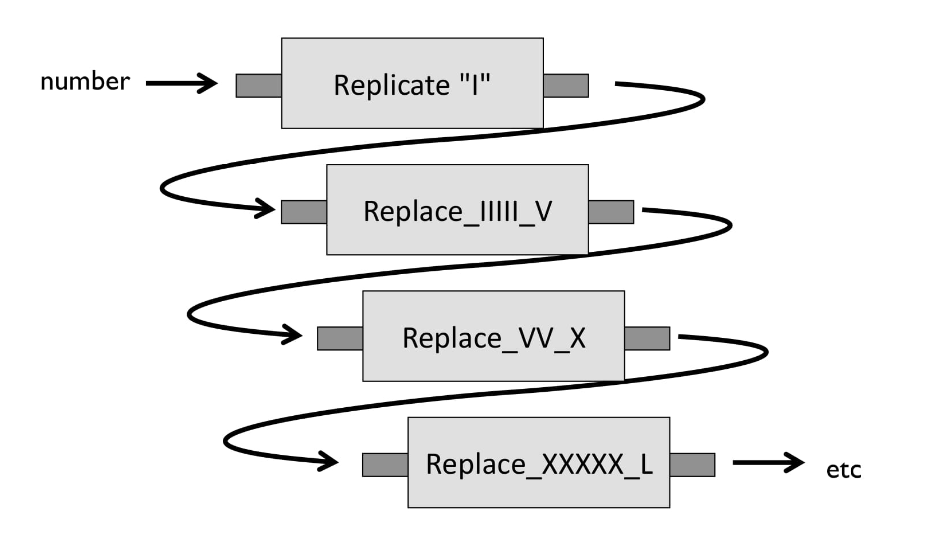
Давайте посмотрим, как мы можем сделать это на C#:

Это код на C# в функциональном стиле. Мы определили несколько маленьких функций, которые потом «пайпнули» с помощью extension-метода Pipe для object.
А теперь на F#. По сути, то же самое,

Как и в C#, у нас есть несколько маленьких функций, которые мы соединяем вместе, но уже с помощью pipe-оператора |>.
Что ж, это были примеры соединения функций (piping), но не всегда всё легко.
Пока что мы имели дело с функциями, у которых одно входное значение и один результат. И при соединении все проходило гладко, они идеально подходили друг другу. Легко!
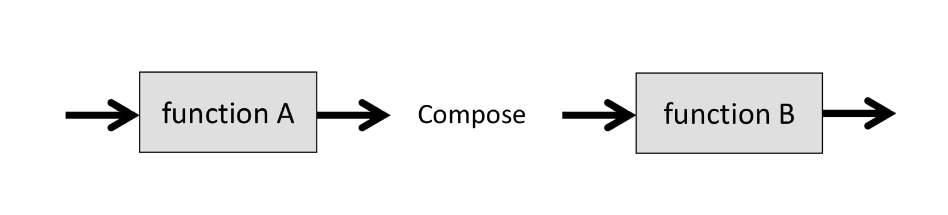
Но в реальном мире всё сложнее.
Например, у нас есть функция с одним результатом и функция с двумя входными значениями.
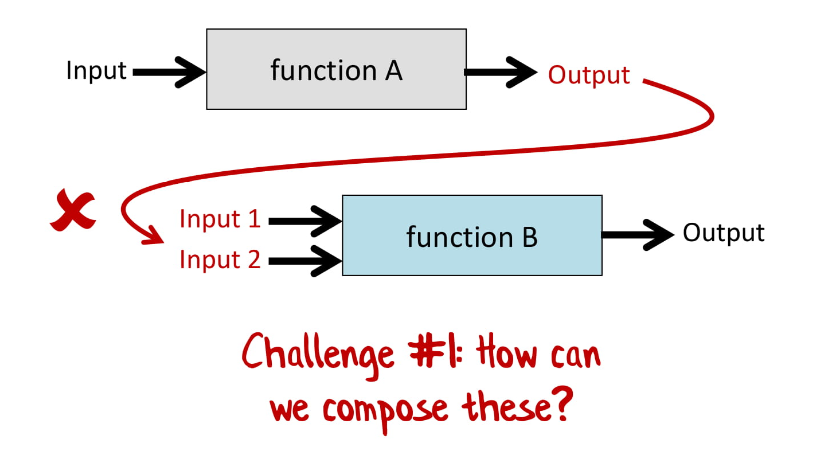
Как же соединить эти две функции?
Композиция с помощью каррирования (на примере римских цифр)
Рассмотрим еще раз задачу о римских числах.
Если посмотреть на функцию String.Replace, она принимает на вход три вещи: исходную строку (inputString), что заменить (oldValue) и на что заменить (newValue).
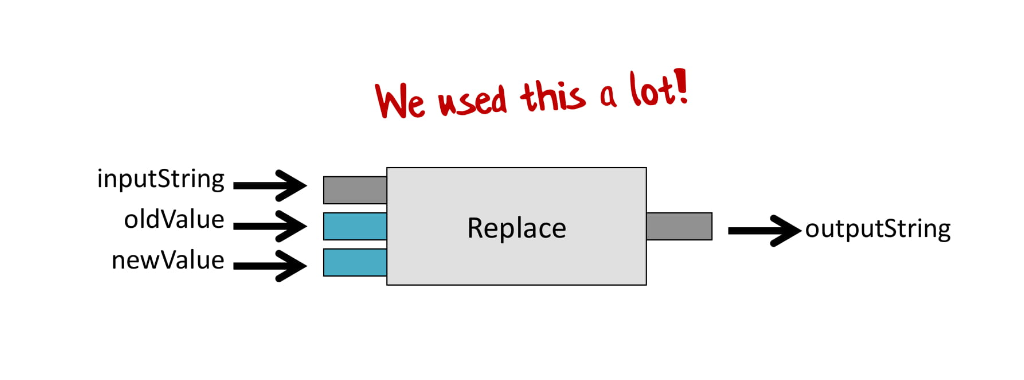
И если мы захотим соединить несколько таких функций, у нас ничего не получится. Мы не можем просто взять результат первой функции и передать его второй, потому что вторая функция ожидает три значения, а не одно.
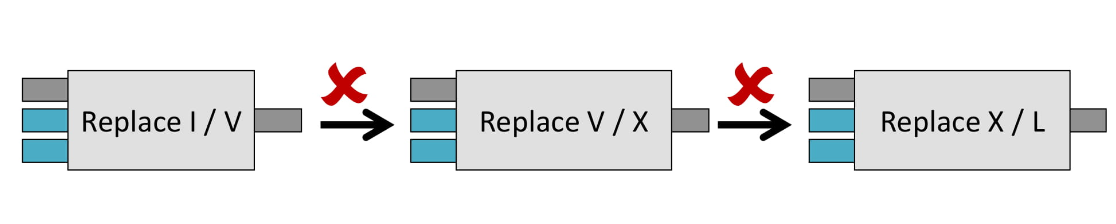
 И вы, наверное, уже подумали, что композиция работает только с функциями, которые принимают одно значение, и это очень плохо, потому что мало какая функция принимает одно значение.
И вы, наверное, уже подумали, что композиция работает только с функциями, которые принимают одно значение, и это очень плохо, потому что мало какая функция принимает одно значение.
Однако есть небольшая хитрость! Любую функцию можно превратить в функцию с одним входным значением. Для этого используют каррирование. Этот метод назван в честь американского математика и логика Хаскелла Карри (Haskell Curry), так что здесь нет ничего общего с индийской кухней.
У нас есть функция с двумя входными значениями. Чтобы превратить ее в функцию с одним входным значением, мы создадим каррированную версию этой функции, которая принимает одно значение, а возвращает новую функцию, которая принимает еще одно значение.
Помните, я говорил, что раз функции — это сущности, то их можно возвращать?
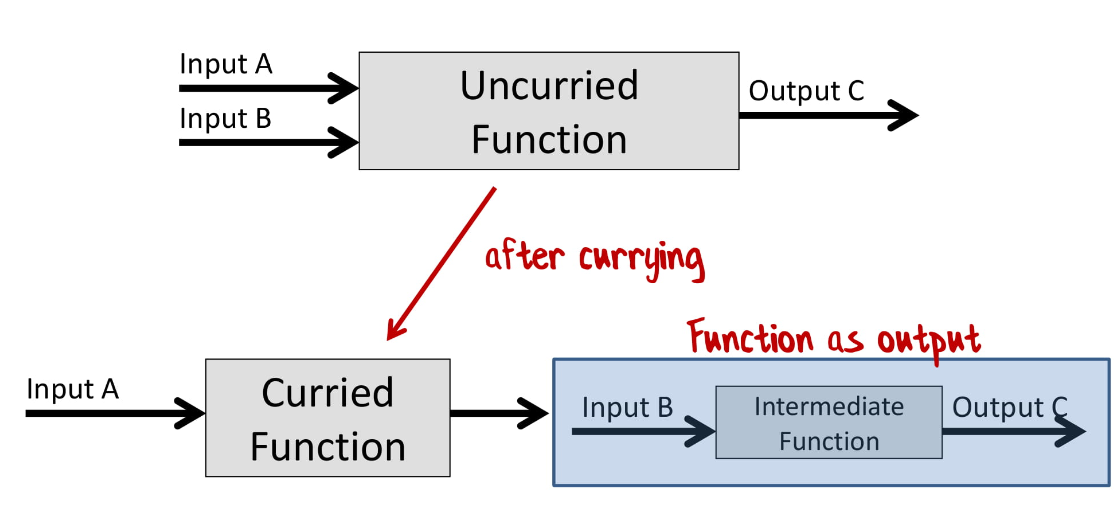
Теперь у нас есть функция, которую мы можем использовать для композиции!
Это и есть каррирование.
Вернемся к Replace. Изначально это функция с тремя значениями, что для нас нехорошо.
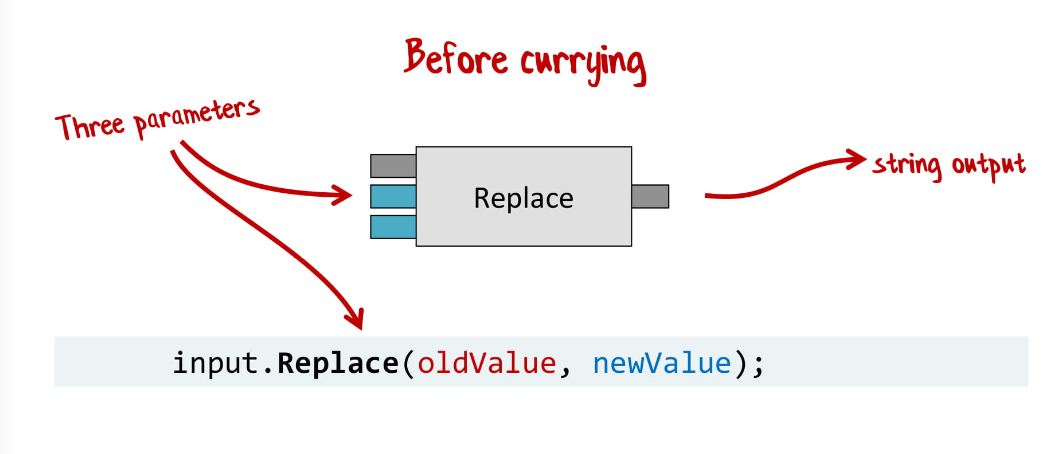
Перепишем ее с помощью каррирования. Я хочу специальную функцию с двумя входными значениями, результатом которой является функция с одним параметром. Вот как это выглядит, если использовать C# в функциональном стиле:
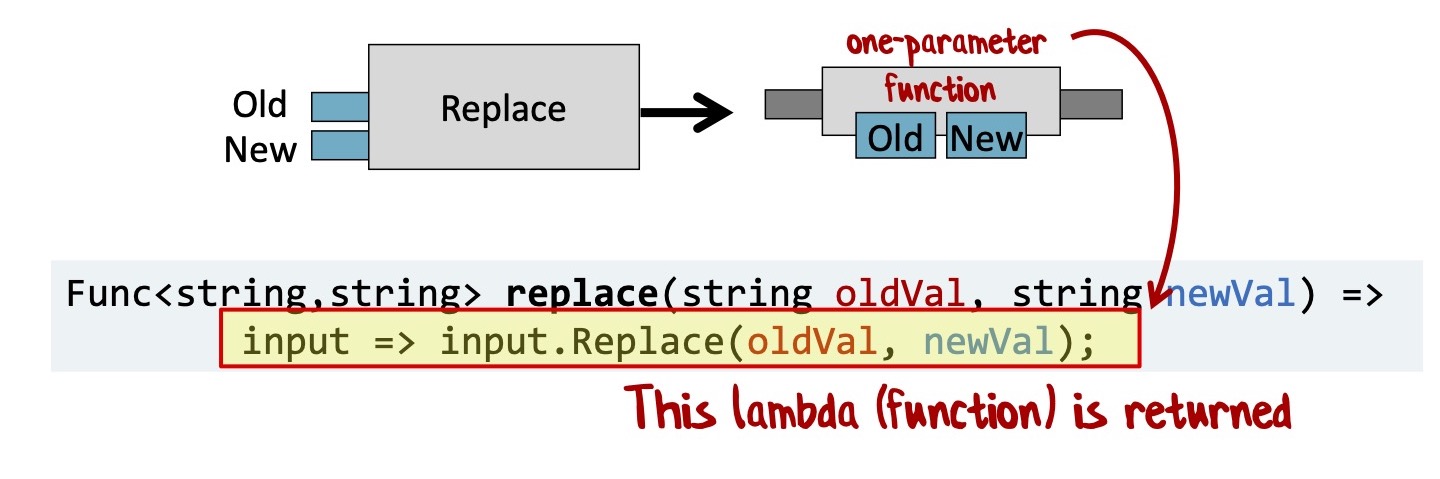
Это функция с двумя входными параметрами, результат которой — лямбда, которая принимает string и возвращает string.
От всего этого с непривычки может болеть голова, выглядит странно, зачем вообще такое писать? При таком подходе для решения задачи с римскими числами нам не надо писать множество маленьких функций, достаточно одной. Выглядит сложновато, но стоит вникнуть — и все станет очень просто.

И теперь при выстраивании пайплайна мы используем одну и ту же функцию, просто с разными значениями.
На C# это все смотрится немного некрасиво, так что давайте посмотрим на F#.

В F# вам не нужны вспомогательные функции, потому что там мы получаем каррирование «из коробки».
Мы просто можем вызвать Replace с двумя параметрами. Но как так, ведь там требуются три?
Частичное применение (Partial application)
Это очень важная техника, при которой мы передаем только часть параметров в функцию.

Например, у нас есть две функции, add и multiply. У каждой из них по два параметра, и обычно нам надо передать все параметры сразу. Но в F# вы можете передать один.
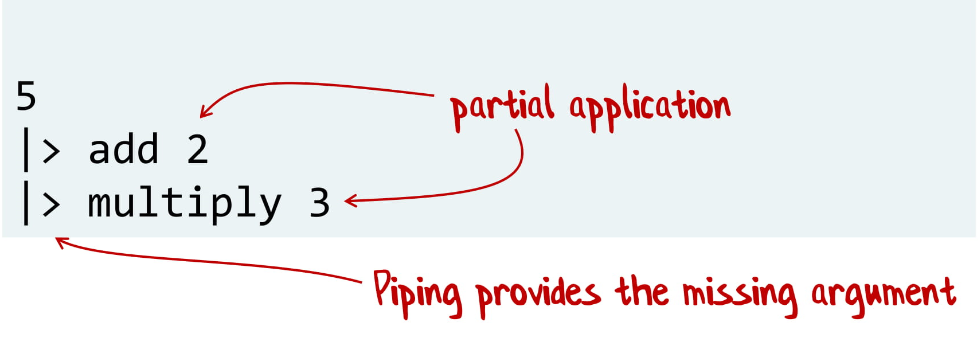
Здесь мы берем число 5 и «скармливаем» его в add, после берем результат и передаем в multiply. Заметьте, что add и multiply принимают только один параметр, а второй приходит из pipe-оператора.
И такое очень часто можно увидеть в функциональном программировании, когда вы передаете только часть параметров, а остальные приходят где-то в другом месте.
Поэтому в F# между параметрами стоят пробелы. Обратите внимание: нет никаких скобок и запятых. И можно обрезать некоторые параметры, сделав новую функцию.
И вот как как выглядит replace с частичным применением. Мы просто передаем два параметра и получаем новую функцию, куда оставшиеся значения приходят из pipe-оператора.
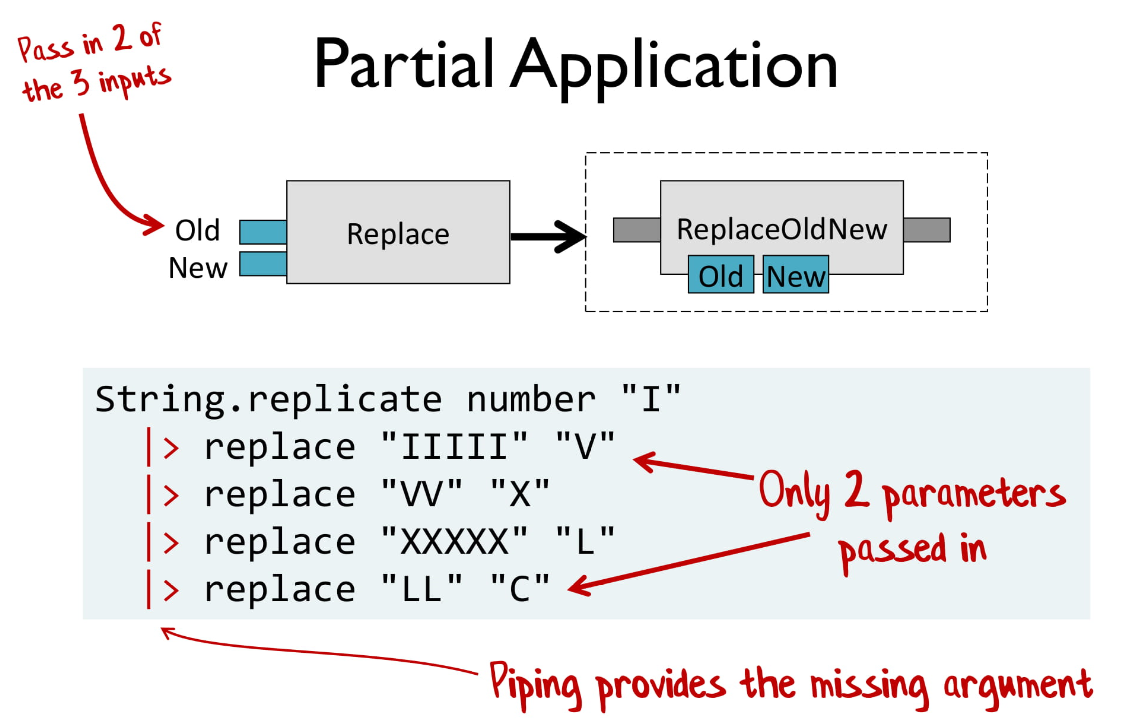
У вас уйдет какое-то время, чтобы вникнуть во все это, потому что это сильно отличается от объекто-ориентированного подхода.
В JavaScript частичное применение доступно с помощью функции bind.
Композиции расширяемы
Композиции также хороши тем, что они расширяемы. Если мы посмотрим на наш код для решения задачи о римских числах, можно заметить, что мы не учли одной детали. При написании римских чисел мы обычно не пишем "IIII", вместо этого пишем "IV", а вместо "VIIII" пишут "IX", и наша программа этого не учитывает. Однако при композиции мы просто можем добавить это все в конец:

При этом мы не трогаем наш старый код. И это очень хорошо, ведь последнее, что хочется делать — это изменять уже написанные куски программы, можно сломать там что-то. Можно добавлять код, удалять — еще лучше, а вот менять хуже. И при композиции можно добавить код наверх, вниз или даже посередине, но важно, что вы не изменяете код, поэтому, скорее всего, ничего не сломается.
Что ж, мы разобрались, как соединить функции, у которых множество входных значений. Ответ — каррирование и частичное применение.
Композиция с помощью Bind (на примере FizzBuzz)
Вообще говоря, почти все задачи в функциональном программировании — о том, как правильно объединить функции. И паттерны в функциональном программировании нацелены на то, чтоб соединять такие, которые изначально «не подходят» друг другу.
Рассмотрим случай, когда функция возвращает два значения, и нам надо соединить ее с функцией, принимающей одно значение:
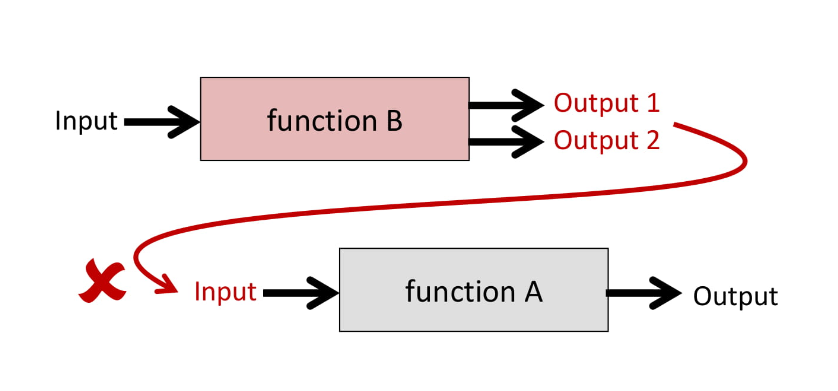
Наверное, все знают задачу FizzBuzz. Вы выводите числа от 1 до 100, но:
- вместо чисел, кратных трем, вы пишете "Fizz"
- вместо чисел, кратных пяти — "Buzz"
- а если число кратно и трем, и пяти, то "FizzBuzz"
Вот как эта задача решается на F#:

На C# будет то же самое. Просто проверяем каждое число в цикле с помощью if else.
Это очень простая реализация FizzBuzz, и если вас попросили решить эту задачу на собеседовании, то лучше написать ее именно так. Но мы решим ее иначе, потому что эта реализация очень легкая, а мы — функциональные программисты и хотим сделать эту задачу настолько сложной, насколько это вообще возможно. Отмечу, что идея взята из блог-поста, призывающего не слишком усложнять FizzBuzz во время реальных собеседований.
Причина, по которой нас не устраивает легкая реализация, заключается в том, что это не композиция, и, если мы захотим поменять что-то, то нам придется изменять уже написанный код. Это не очень приятно, лучше сделать так, чтобы мы могли добавлять код в наш пайплайн.
Сделаем такой пайплайн, соединив несколько маленьких функций:
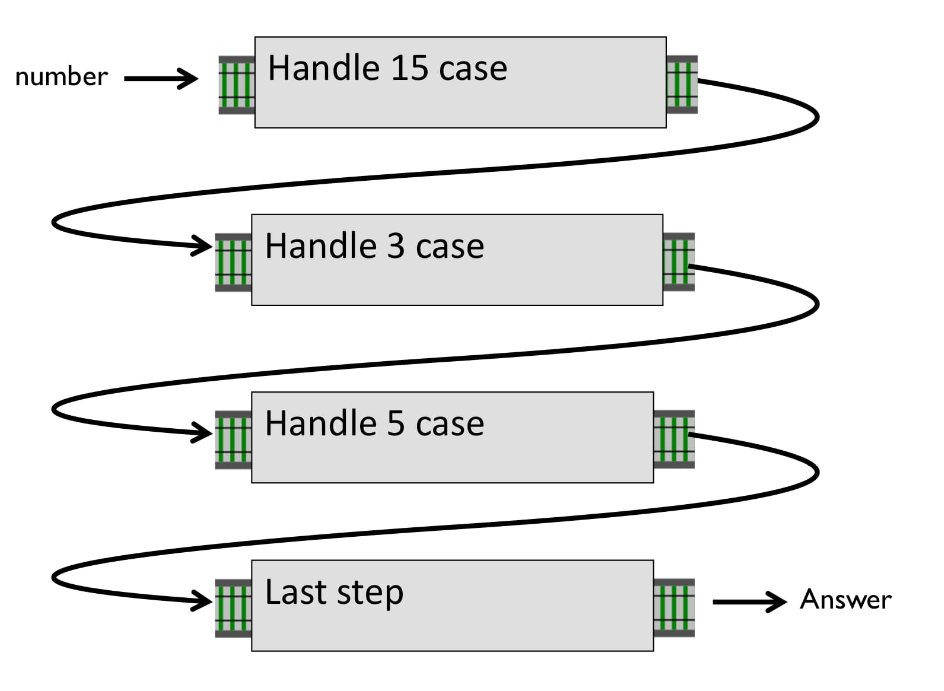
Сначала мы проверим на кратность 15, потом на кратность 3 и т.д. И если мы захотим что-то поменять, сможем просто добавить функции в наш пайплайн.
В отличие от задачи о римских числах, когда мы разбираем каждое число, есть два возможных варианта: в качестве результата может быть либо то же самое число, либо строка («Fizz», «Buzz», «FizzBuzz»).
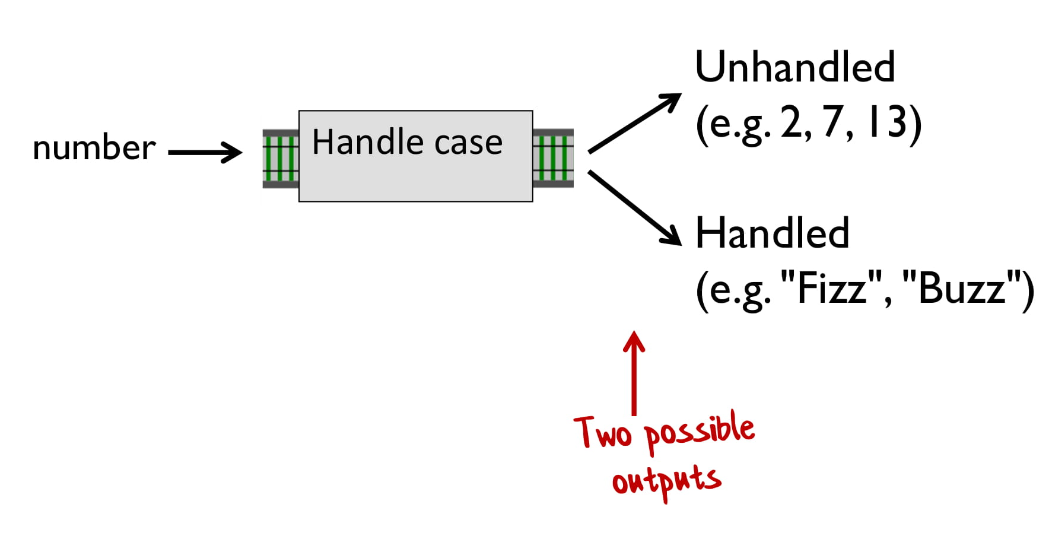
Если функция вернула строку, будем говорить, что вернулось обработанное значение, иначе — необработанное значение.
Если представить, что наша функция — это часть железной дороги, то это была бы развилка, где первая ветка (зеленая) — это необработанное значение, а вторая (красная) — обработанное.
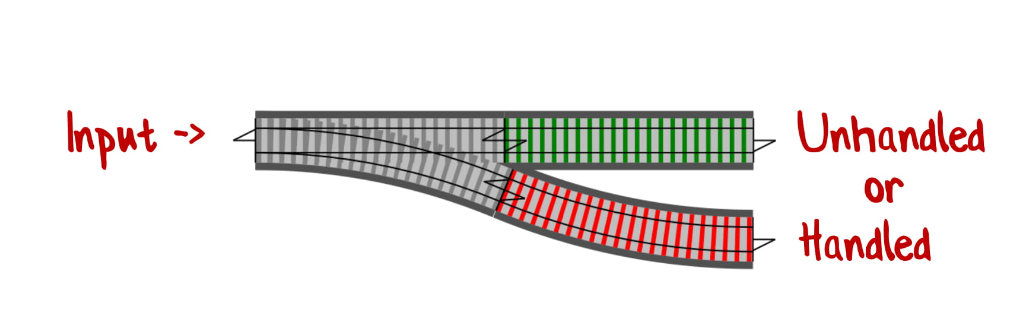
Заметьте, что результатом функции может быть обработанное ИЛИ необработанное значение. Слово «или» здесь ключевое.
Мы уже знаем, что в F# за «ИЛИ» отвечают choice types. Сделаем и тут такой тип, который может включать как int, так и String.

Теперь опишем функцию handle, обрабатывающую каждый случай.

Эта функция проверяет, делится ли число n на число divisor без остатка, и, если делится, то возвращает обработанную строку label, иначе возвращает необработанное число n. Обратите внимание, что функция принимает три входных значения.
По сути это логика, которая была в легкой версии FizzBuzz, вынесенная в отдельную функцию. Посмотрим, как ведет себя эта функция на реальных примерах:
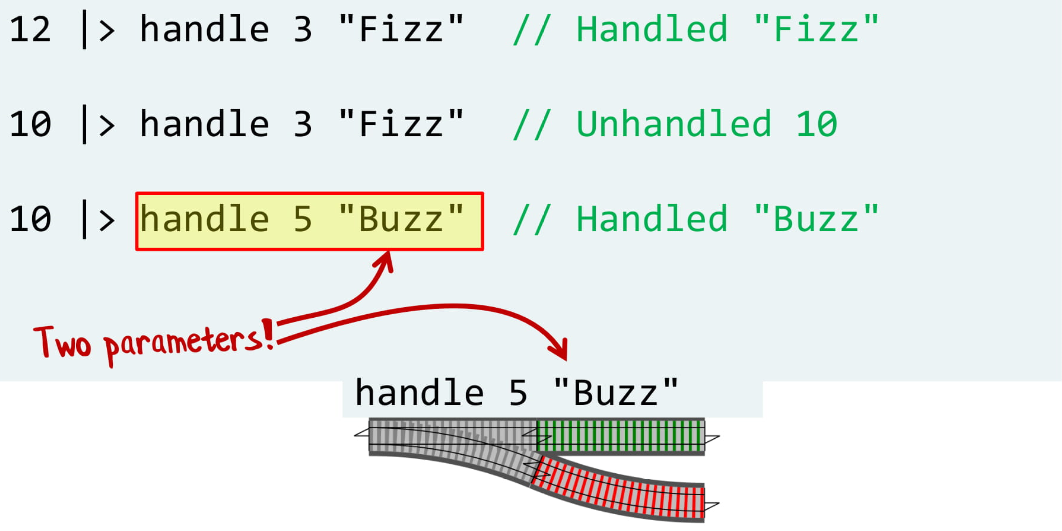
Сначала мы проверяем, делится ли 12 на 3, и если делится, возвращаем обработанную строку «Fizz», поэтому в первом вызове мы получили обработанный «Fizz».
Потом в эту же функцию передаем 10, и получаем необработанную 10, потому что 10 не делится на 3.
И, наконец, 10 проверяем на кратность 5 и получаем обработанный «Buzz».
Обратите внимание, что мы используем функцию handle с 2 параметрами, и если проводить аналогии с железной дорогой, это является развилкой, которая определена 2 параметрами.
Теперь сделаем первую попытку реализовать весь FizzBuzz с помощью композиции:

Сначала мы проверяем, делится ли n на 15, и в качестве результата получим FizzBuzzResult, который потом мы проверяем с помощью match.
Если вернулось обработанное значение, то функция возвращает итоговый результат, если необработанное — проверяем, делится ли n на 3, и повторяем все то же самое. И только если наше n не делится на 5, то возвращается само число n.
На самом деле так писать не надо, это очень плохой код. Но как нам сделать его лучше?
Здесь можно заметить закономерность. На каждой проверке мы встречаем одну и ту же инструкцию: «если результат — необработанное число, сделай что-то».
По сути, она представляет собой это:

Если обработано, то верни значение, если не обработано, то сделай что-то.
Вспоминая аналогию с железной дорогой: если мы остаемся на пути «необработанное значение», то продолжаем ехать по пайплайну, но если свернули на «обработанное значение», то пропускаем весь наш пайплайн и возвращаем результат.
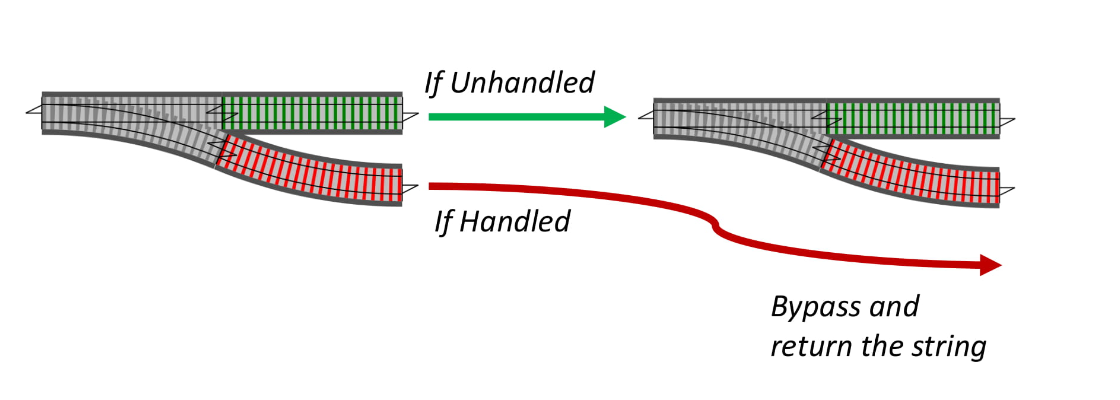
Мы напишем небольшую вспомогательную функцию.
Она говорит: Если result — обработанное значение, то мы просто «проезжаем до конца дороги», но если result — необработанное значение, то нам надо сделать что-то.
Но что именно сделать? Мы сами ещё не знаем. Поэтому вынесем это в отдельную функцию и будем принимать ее в качестве параметра:

В этой функции то, что понадобится делать дальше, если result окажется необработанным. И причина, по которой она называется «f», заключается в том, что мы не знаем что это за функция, это может быть что угодно! Можно было назвать её «следующий участок железной дороги».
И с помощью этого можно изменить нашу оригинальную реализацию. Можно сказать: попробуй это, если результат остался необработанным — переходи ко второму шагу, если и после него необработанным — к третьему, и затем последний шаг.

Мы как бы едем по железной дороге и каждую развилку спрашиваем себя: «Мы до сих пор на зеленой (необработанной) ветке?», если да, то продолжаем ехать, если нет, то «выезжаем» с результатом. А lastStep — это место, где дороги сходятся вместе и возвращается результат:

Теперь мы сделали все пайплайном, и благодаря композиции все легко расширять. Можно добавлять новые проверки, не трогая старый код — достаточно будет просто добавлять функции. Кроме «fizz» и «buzz», легко добавить что угодно и быть уверенным, что оно заработает:

Это применимо и в той типичной ситуации, когда мы запускаем Task, если эта задача завершилась, то запускаем следующую, а в противном случае просто «проходим в конец». Ну, promise, future, async, вот это все.
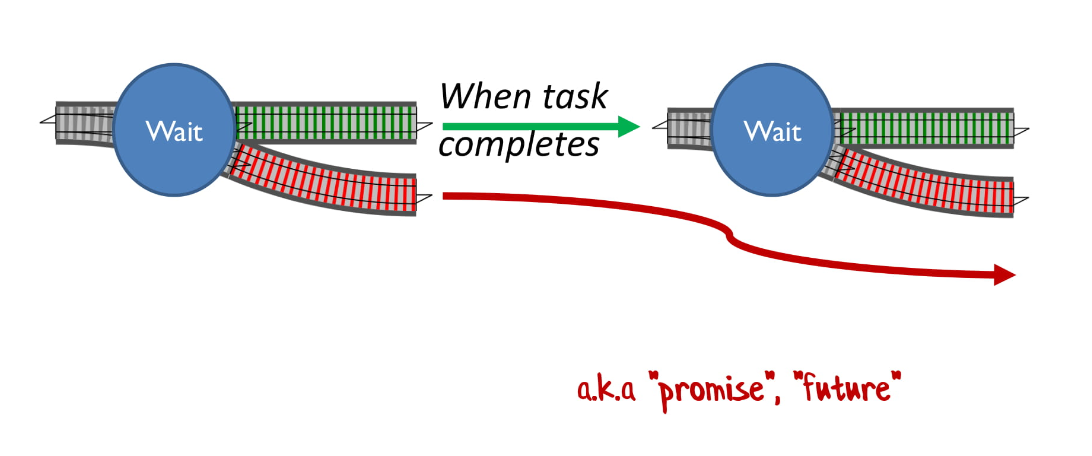
Вы часто видите код, где начинается Task, после завершения запускается следующий, потом следующий, и так далее. В итоге вы получаете глубоко вложенные функции, и чем больше функций, тем хуже это выглядит и тем сложнее это читается.
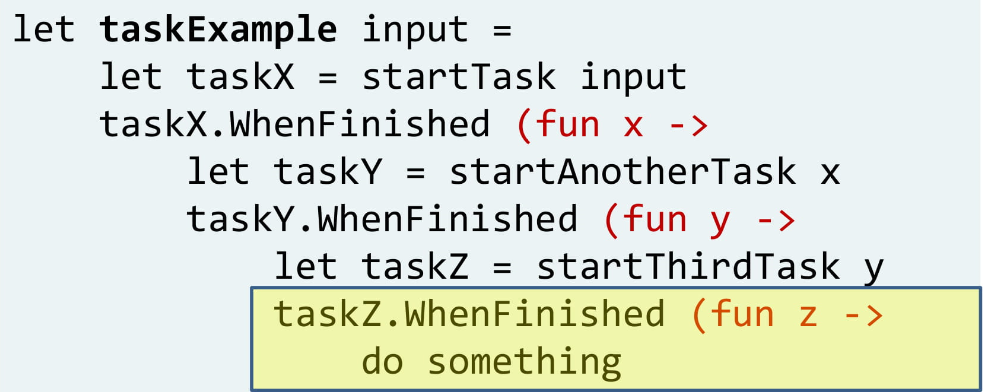
Заметьте, здесь тот же паттерн, что и в FizzBuzz: «когда Task завершится, сделай что-то». Поэтому, чтобы исправить ситуацию, мы сделаем то же самое: напишем вспомогательную функцию:

Когда task завершится, сделай что-то — и мы не знаем, что конкретно, поэтому принимаем для этого функцию f.
Теперь мы можем переписать наш код с использованием нашей новой функции:

Теперь мы по-прежнему последовательно запускаем задачи, но у нас появился очень хороший «плоский» пайплайн, мы избавились от вложенной вложенности, код стал намного читабельнее, стало легче добавлять и убирать функции.
И это подводит нас к следующей теме:
МОНАДЫ!

Все очень боятся монад, но сегодня мы не будем учить монады, наша цель просто перестать бояться их, чтобы не впадать в панику каждый раз, когда вы слышите это слово.
Что же такое монада?
Монада — это просто общее решение вышеописанных проблем. Если конкретнее, существует понятие Bind.
Очень часто вы сталкиваетесь ситуацией, когда у вас есть функции с «ветвями», и вы хотите их соединить. Начинаете вы с такого:
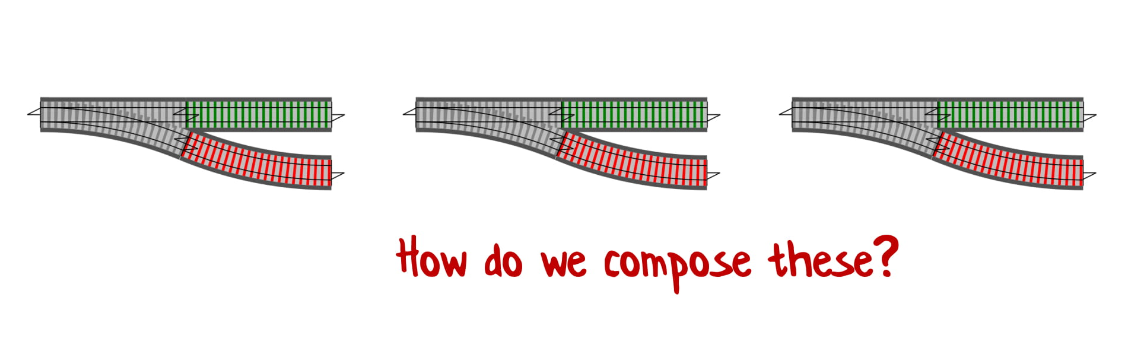
А в итоге у вас получается это:

Я называю такой подход «Railway Oriented Programming» и посвятил ему отдельную страницу на сайте (перевод доступен на Хабре). Это особенно применимо для обработки ошибок, но не только для них.
Если у нас функции с одним входным значением и одним результатом, то они отлично соединяются:
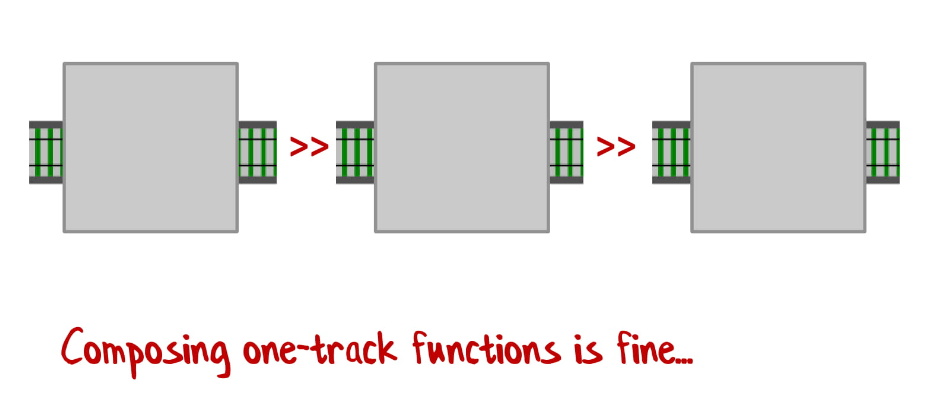
Если у вас функция с двумя входными значениями и двумя результатами, то мы тоже можем их легко соединить:
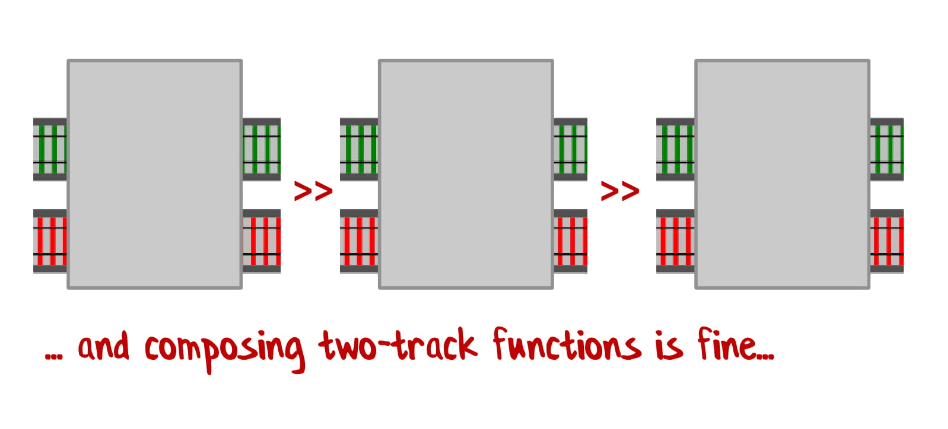
Но у нас вот такая ситуация:
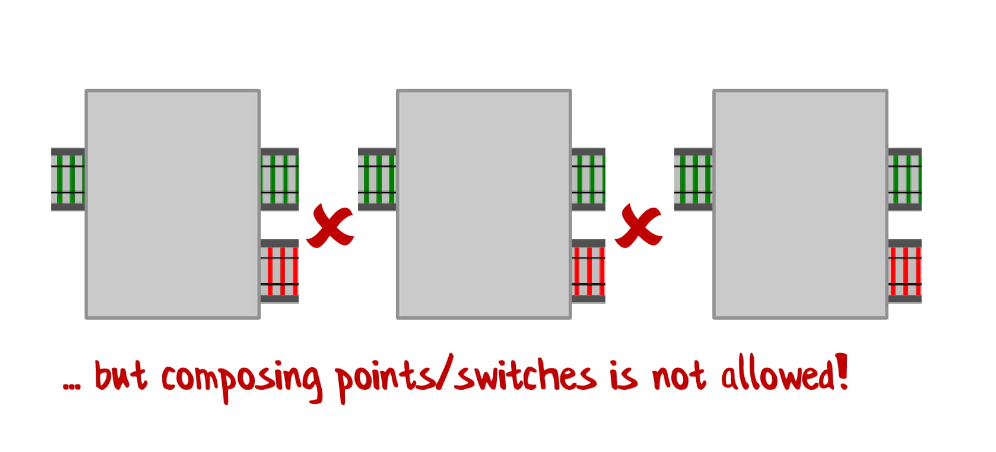
У нас одно входное значение, два на выходе и они не соединяются!
Что же нам сделать для решения этой проблемы?
У нас есть один «вход» и два «выхода»:
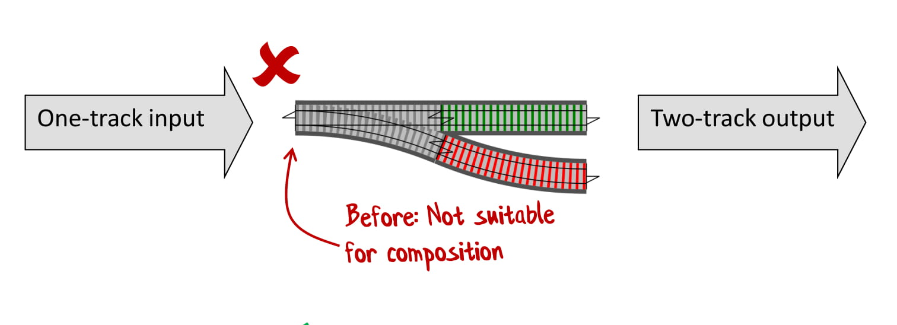
А если бы было два «входа» и два «выхода» — это было бы прекрасно, такие конструкции мы можем очень легко соединить:
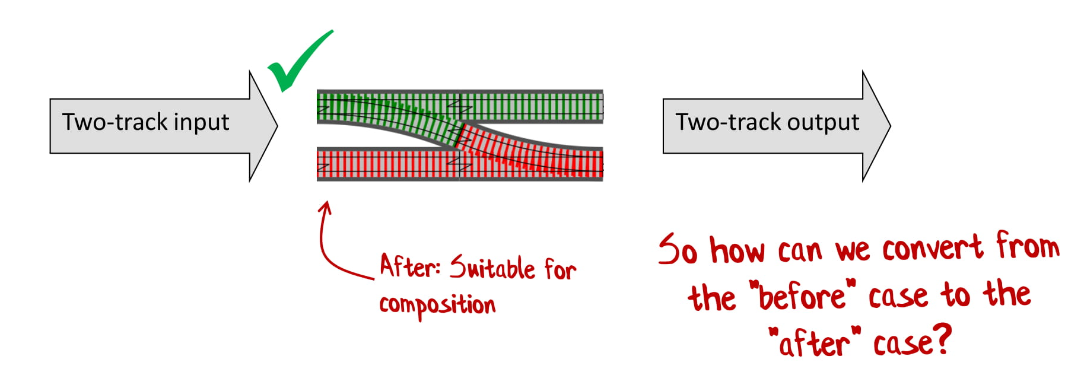
И нам нужен способ превратить первую функцию во вторую. Для этого мы напишем адаптер.
Если у вас была когда-нибудь игрушечная железная дорога — это то, что вы вполне могли видеть. У вас есть ячейка, в которую вы помещаете вашу функцию или часть железной дороги, и теперь у вас два «входа» и два «выхода»:

Это преобразователь функций! Помните, как мы говорили, что функции могут быть входными значениями и результатами выполнения? Так вот адаптер — это функция, которая превращает один тип функций в другой.
Очень важная штука и обычно ее называют Bind, хотя есть разные варианты.
Это сложнее объяснить, чем показать — там обычно всего несколько строк кода, а я тут час распинаюсь.
Давайте посмотрим, как это работает на нашем примере обработанных и необработанных значений.
Мы получаем наше входное значение и, если оно «необработанное», мы запускаем функцию:

Однако, если наше входное значение зашло с «красной дороги», мы ничего не делаем:

Если вы обратили внимание, то bind — это абсолютно то же самое, что и наша вспомогательная функция ifUnhandledDo для FizzBuzz.
В терминологии функционального программирования мы используем слово «монада», что обозначает просто общий подход для решения таких проблем, состоящий из трех элементов:
- тип данных (у нас был FizzBuzzResult)
- связанная с ним bind-функция (у нас была ifUnhandledDo)
- и некоторые другие штуки
И, по сути все, это и есть монада. Конечно, это все немного непривычно и для каждой задачи есть свои монады, но все они используют один общий подход.
Еще вы иногда слышите о монадических функциях.
Это функции, у которых есть «ветви» и которые используют bind. В нашей задаче это функция handle, которая проверяет число на кратность другому числу и, в зависимости от результата, возвращает либо «обработанное» значение, либо «необработанное».
Теперь мы решили проблему «Можем ли мы соединить функции с двумя результатами и одним входным значением?» Да, можем! С помощью монад.
Композиция Клейсли (на примере веб-сервиса)
Последнее на сегодня. Есть и другой способ соединить «пути»: можно просто оставить в покое одно входное значение и два результата, тогда у нас получится часть железной дороги такой же формы, как две исходных.

Эту технику мы используем для написания веб-приложения.
Для начала напишем HttpHandler, который будет обрабатывать запросы.

На вход будет передаваться HttpContext, который содержит и Request, и Response, и Cookies, и много чего еще. А вернется Async<HttpContext option\>. Это значит, что результата может не быть, ваше веб-приложение может и не справиться с какими-то запросами. Так что мы просто говорим, что результат опционален (если получилось, мы на зеленом пути). И все это асинхронно.
Если вам интересно посмотреть на фреймворк, основанный на этой концепции, то поищите F# Giraffe. Он основан на ASP.NET, но использует этот подход.
Такой способ соединения функций, который в результате дает функцию такого же типа, называется композицией Клейсли. У него есть свой символ >=>

Здесь хорошо вписывается аналогия с Lego: вы соединяете две детали и получаете новую деталь. И из-за того, что новая деталь все еще является деталью Lego, вы можете соединять ее с другими деталями, и вы можете продолжать до бесконечности, но на каждом шаге вы будете получать один и тот же тип (деталь Lego).
Начинаем писать веб-приложение: как водится, сначала маленькие части, а потом из них сделаем большие. Вот маленькая часть, и все, что она делает — проверяет, совпадает ли путь из Request с указанным:

То есть, если путь "/hello", то эта часть успешно выполнится, а, если нет — то провалится.
Вот еще одна часть, она возвращает код 200 и строку «Hello», и всегда выполняется успешно.

Теперь соединим эти части вместе и в итоге получим новую функцию, которая является их комбинацией:

То есть мы составили функцию побольше, которая возвращает код 200 и сообщение «Hello», из функций поменьше, и мы можем продолжить!
Интересная вещь choose. Она работает так: у вас есть несколько вариантов, и choose просто выбирает первый, который сработает.

Например, мы можем проверять путь на «/hello», и если он совпадает, возвращать «Hello»; также мы можем проверять путь на «goodbye», в этом случае вернется «Goodbye», а если ничего из этого не подходит, то мы просто ничего не вернем, потому что результат «опционален».
Также рассмотрим функцию, которая успешно завершается только в случае, если приходит GET запрос:

Теперь мы возьмем эту функцию и соединим ее с choose: если у нас GET-запрос — мы начнем проверять пути, если у нас не GET-запрос — до этого выбора не дойдет.

Теперь наша функция стала еще больше.
Продолжаем дополнять ее за счет POST. Теперь у нас есть обработка GET-запросов и POST-запросов, осталось добавить выбор между ними, и все, у нас есть готовое простенькое веб-приложение!

И вся программа — это просто огромная функция, все части которой могут быть использованы повторно, их можно легко добавлять и удалять, проводить тестирование независимо от остальных частей и т.д. Как с Lego.
Когда вы пишете свое веб-приложение — вот как оно выглядит:

Несколько маленьких функций и никаких классов, никакого наследования, все данные «текут» в одном направлении. Это то, как пишутся приложения в функциональном стиле, исключительно с помощью композиций, пайплайнов и маленьких функций.
Это и есть сила композиции!
Итоги
Мы поговорили о философии, которая стоит за композицией, а именно — что все части можно соединить и использовать повторно. Просто подумайте о Lego: если что-то характерно для него, то характерно и для функционального программирования.
Поговорили о принципах функционального программирования, о функциях и типах, которые можно соединять.
Мы рассмотрели множество техник композиции:
- Самое простое — связать все в пайплайн с помощью |>.
- Если функции не очень «подходят» друг другу, то можно использовать каррирование/частичное применение.
- Также вы можете использовать монады для композиции.
- Ну и, конечно, вы можете применять композицию Клейсли.
На данном этапе вы, возможно, и не все поняли, потому что на самом деле здесь очень много материала для одного часа. Но надеюсь, что вы хотя бы перестали бояться всех этих слов — таких, например, как монады. И увидели в них потенциал и пользу.
Но зачем мне все это?
Мноиге скажут: я уже знаю C#, умею писать в объектно-ориентированном стиле. Зачем мне все это? FizzBuzz стал только сложнее прежнего. Оправдана ли эта лишняя морока?
С FizzBuzz, пожалуй, действительно перебор. Но в целом я вижу у композиции весомые плюсы:
- Переиспользуемость. Такой подход заставляет вас писать код, который можно использовать повторно. А мы как разработчики всегда к этому стремились.
- Тестируемость. Каждая часть может быть протестирована независимо от других частей.
- Понятность. То, что данные «текут» только в одном направлении, делает ваш код читабельнее.
- Поддерживаемость. Каждый параметр передается в функцию, нет никаких глобальных переменных и неявных зависимостей.
- Расширяемость. Очень удобно добавлять что-то. На примере FizzBuzz можно увидеть, что несмотря на то, что изначально его было сложнее написать, мы могли очень легко добавить новые части.
- И самое важное: это другой способ мышления! Очень полезно заставлять себя думать по другому. Многие люди, которые учат функциональное программирование даже без применения его на работе, становятся лучше в C#, потому что они начинают думать по другому. Это главный плюс!
На новом DotNext Скотт выступит с докладом «Design with Capabilities», а я поучаствую в этом как приглашенный эксперт. Еще функциональную тему разовьет Вагиф Абилов: расскажет о такой экзотике, как фронтенд на F#. Ну и, как обычно, будет просто много всего для .NET-разработчиков. Конференция начнется уже завтра, так что если интересно — поторопитесь!


AnonimBlet228
Спасибо за прекрасный перевод!