03.05.2021 08:01
owlofmacloud 18 16100 Источник

Принцип запрета Паули с однозначной многочастичной волновой функцией эквивалентен требованию, чтобы волновая функция была антисимметричной по отношению к обмену частицами. Как это объяснить на пальцах? Легко - ткните пальцем в стол, в монитор, во что-нибудь твердое. Глубоко пронзили материю? Удалось достичь перекрывания атомных электронных облаков пальца и стола? Нет? Не удивительно. Читайте дальше, если хотите узнать, почему так.

Спин

Цитата из Википедии: Принцип исключения Паули (принцип запрета Паули или просто принцип запрета) — это квантово-механический принцип, который гласит, что два или более идентичных фермиона (частицы с полуцелым спином) не могут одновременно находиться в одном и том же квантовом состоянии в квантовой системе.

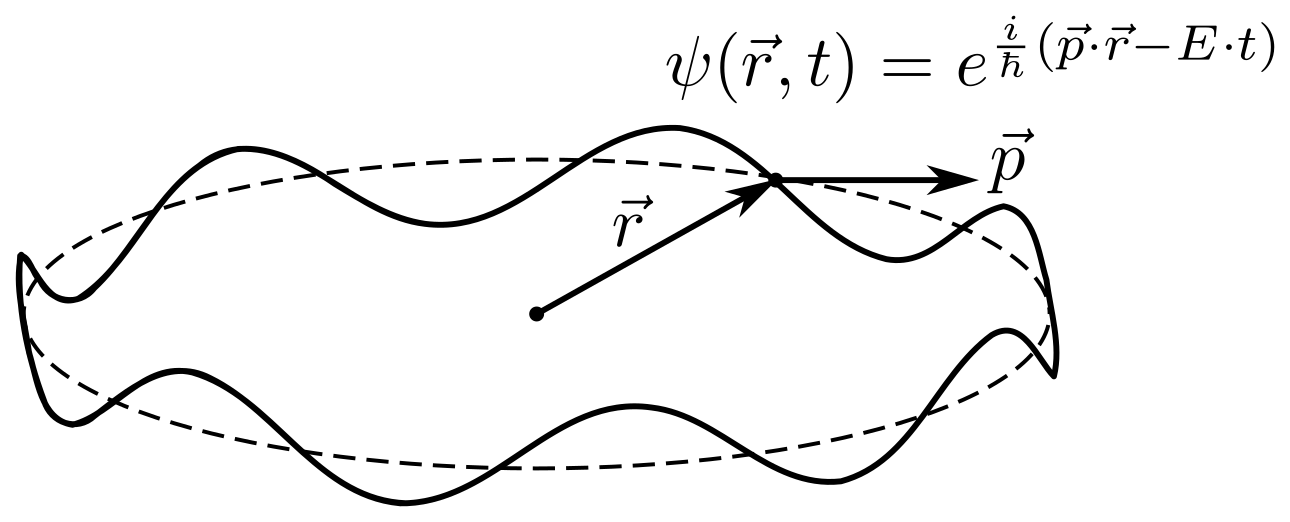
Волновая функция вращающейся частицы.
Волновая функция вращающейся частицы.

Что-то про спин. Начнём с того, что такое спин, в частности, полуцелый спин. Пускай частица движется по окружности длины 2\pi r, а через \vec{r}мы обозначим позицию частицы. Частица будет описываться волновой функцией\psi(\vec{r},t). Для простоты положим, что это самая обычная бегущая волна.

\psi(\vec{r},t)=e^{\frac{i}{\hbar}(\vec{p}\cdot \vec{r}-E\cdot t)}

Волновая функция должна однозначно определяться на окружности, а поворот на

2\pi радиан никак не должен её изменять, то есть:

e^{\frac{i}{\hbar}p\cdot 2\pi r}=1

Экспонента в мнимой степени это тригонометрическая функция, как синус или косинус, по сути мы записали, что волновая функция периодическая. Это возможно только если произведение

p\cdot r=\hbar n, где n - обязательно целое число. Вспомнив, что произведение \vec{l}=\vec{p}\times \vec{r} ничто иное как момент импульса, для нашей частицы мы получаем условие:

l_z = n\hbar
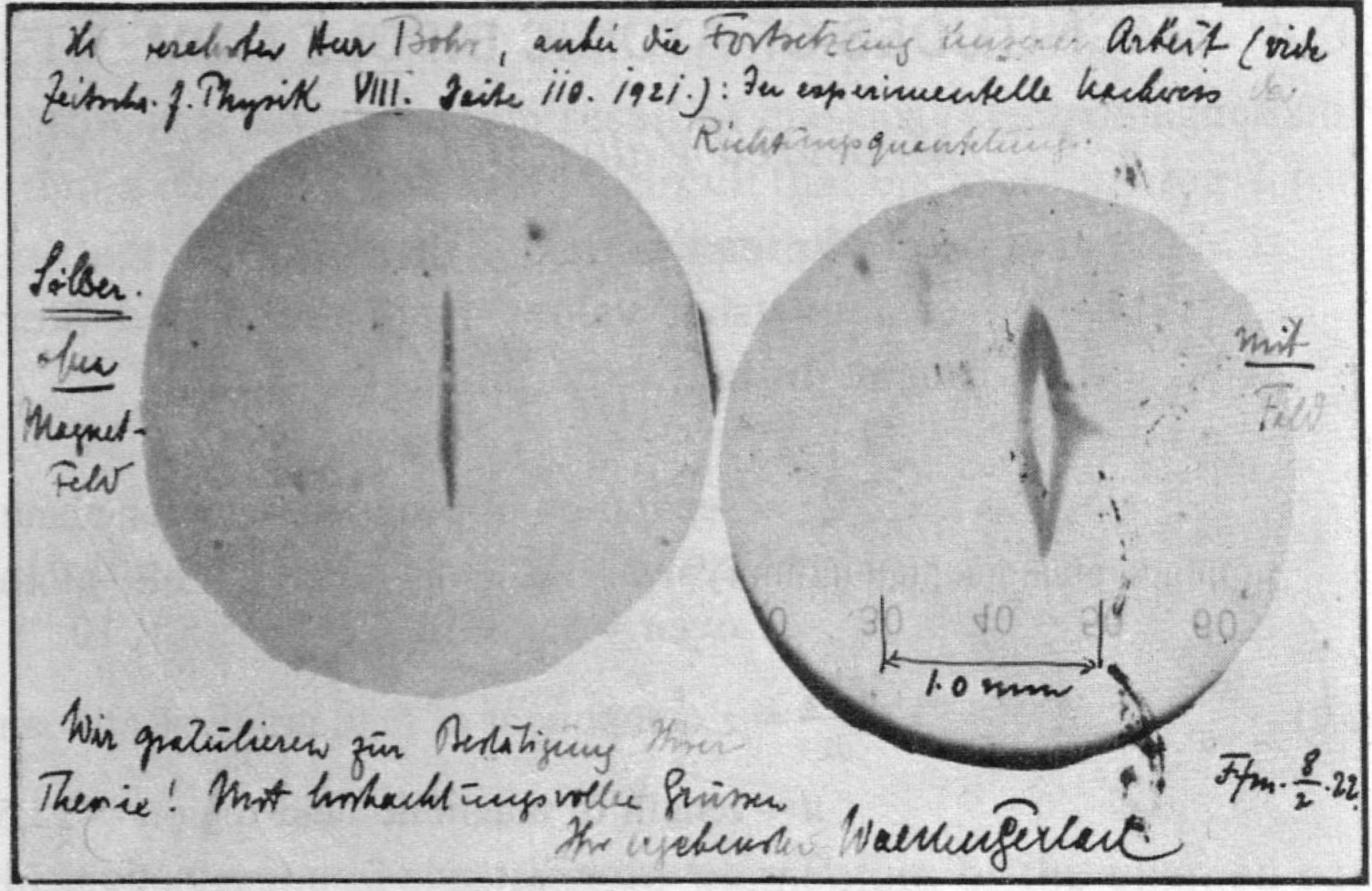
Та самая открытка Нильсу Бору от Отто Штерна и Вальтера Герлаха.
Та самая открытка Нильсу Бору от Отто Штерна и Вальтера Герлаха.

Всё это хорошо, но Отто Штерн и Вальтер Герлах установили, что электрон может так вращаться, что совершив полный оборот он не придёт в тоже самое состояние, что и раньше. А вот если два оборота сделает, тогда всё хорошо. В его случае n=1/2 и он может крутиться с периодичностью 4\pi. Если Вы тоже задали себе этот вопрос: а что, черт возьми, курили эти ученые, то вам поможет удовлетворить любопытство эта статья - Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics.

Вращение тела с периодичностью 720 градусов.
Вращение тела с периодичностью 720 градусов.

Хорошие новости - в трехмерном пространстве есть такой тип вращения. Забавная особенность - такое вращение не перекручивает подсоединенные к телу верёвки. Попробуйте этот трюк в баре с кружкой пива - Вы сможете её постоянно поворачивать не перекручивая свою руку.

Антисимметричность по отношению к обмену электронов

Перестановка двух связанных друг с другом объектов трехмерного пространства эквивалентна повороту одного из них на 360 градусов. Значит, если периодичность вращения объекта 4\pi - то перестановка приводит к смене его волновой функции. Две смены знака: -1\times -1=1.

Обязательную смену знака волновой функции при перестановке двух частиц со спином s=1/2можно трактовать как требование не перекручивать связывающее их пространство [См. Pauli principle in Euclidean geometry]. Эта лента гибкая, но до определенных пределов. Давайте установим предел гибкости нашего пространства-времени на скручивание.

Следующий пример описывается в статье Вайскопф, В. Современная физика в элементарном изложении. УФН 103(1) (1971) 155-179. Пусть есть два электрона с волновыми функциями:

\psi(x_{1})=e^{\frac{i}{\hbar}p\cdot x_{1}},\quad\psi(x_{2})=e^{\frac{i}{\hbar}p\cdot x_{2}}

Забудем пока об электростатическом отталкивании, просто летят два электрона с импульсами

p_1=-p_2 на встречу друг другу. Расстояние между ними x=x_{2}-x_{1}. Волновая функция этой системы электронов:

\Psi(x_{1},x_{2})=e^{\frac{i}{\hbar}p\cdot x_{1}}e^{-\frac{i}{\hbar}p\cdot x_{2}}

однако, она в таком виде еще не обладает свойством антисимметрии. Легко поправить дело:

\Psi=e^{\frac{i}{\hbar}p\cdot(x_{2}-x_{1})}-e^{-\frac{i}{\hbar}p\cdot(x_{2}-x_{1})}

тогда перепишем её как:

\Psi=2i\cdot\sin(\frac{p\cdot x}{\hbar})

Плотность вероятности имеет вид:

\rho(x)=4\cdot\sin^{2}(k\cdot x)

где k=p/\hbar - волновое число. Для всех возможных импульсов со средним значением p_oплотность вероятности \rho(x) есть интеграл по всем волнам с различными значениями k. После интегрирования получаем, что \rho(x) имеет вид ступени.

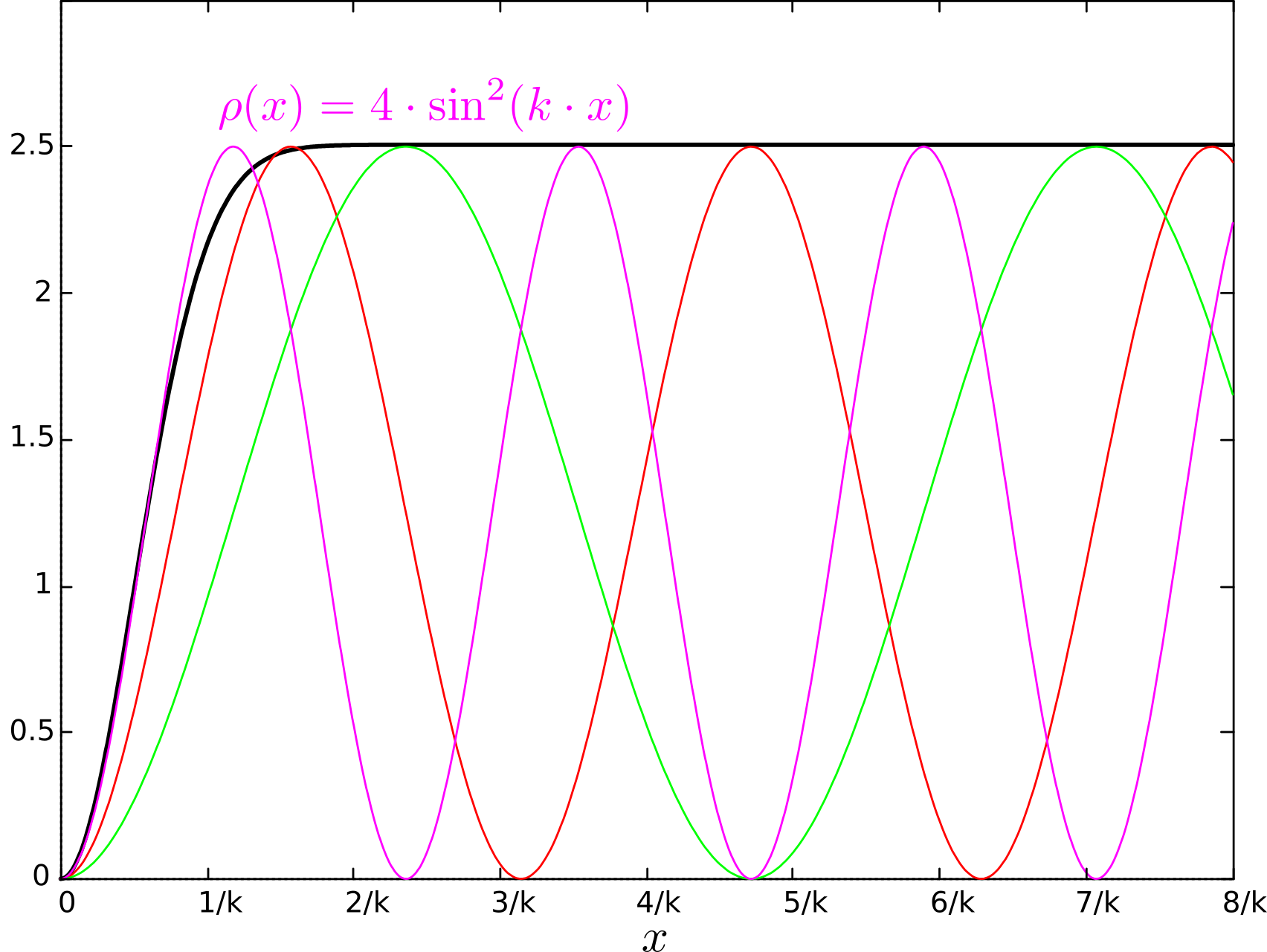
Черная кривая - плотность вероятности для некоего среднего значения импульса.
Черная кривая - плотность вероятности для некоего среднего значения импульса.

Плотность вероятности встречи электронов на расстоянии менее x_{min} стремится к нулю. Минимальное возможное расстояние между ними, как видно, имеет порядок их средней длины волны, т.е. x_{min}\approx 1/k_0. Именно так получается характерный объём пространства, занимаемый электроном. Как будто электрон - упругий шарик.

Принцип запрета Паули

Плотная упаковка электронов в атоме.
Плотная упаковка электронов в атоме.

Расположим шарики-электроны плотной упаковкой, т.к. положительно заряженное ядро стягивает их к себе, а принцип Паули и кулоновское отталкивание мешают подходить им близко друг к другу. В полученной структуре шарики расположены слоями - наружный слой, средний, внутренний. Места в пространстве у шариков однозначно задаются адресами из трех целых чисел. (Подробнее см. в Stevens, P.S. A Geometric Analogue of the Electron Cloud. Proceedings of the National Academy of Sciences 56(3) (1966) 789-793.) Смотрите на картинку.

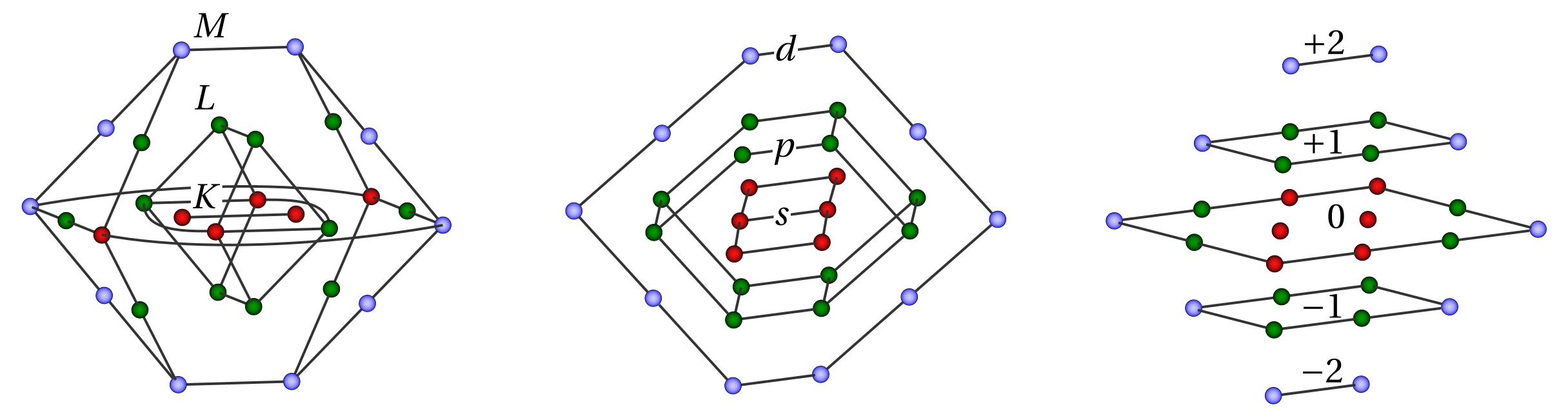
Оболочечная структура атома: главное квантовое число, орбитальное число и магнитное число.
Оболочечная структура атома: главное квантовое число, орбитальное число и магнитное число.

Если считать, что четвертое число - окраска шара (черная/белая, спин +1/2 или -1/2), получим, что принцип запрета Паули (нет двух электронов в атоме с одинаковым набором четырех квантовых чисел) эквивалентен однозначности адресации шара в плотной упаковке.

В свою очередь, атомы в веществе, как правило, стремятся плотно заполнить пространство. Пустого места нет, и метафора с электронными облаками, а облака могут проникать друг в друга, здесь неуместна. Материя плотная и мы это чувствуем физически.

Октет Льюиса, двойной квартет Линнета

Стремление к заполнению оболочки (правило 8 электронов, правило 18 электронов) есть ничто иное, как попытка электронов атома выстроить максимально плотную и симметричную структуру. Более того, октет Льюиса как раз исторически произошёл от кубической модели атома. С появлением квантовой механики о кубе забыли, но правило октета осталось в школьных учебниках.

В 1961 году Линнет выдвинул интересную модификацию правила октета Льюиса (см. Дей К., Селбин Д. Теоретическая неорганическая химия. М.: "Химия" 1976. Стр. 197). Он предположил, что ключевым принципом построения оболочки должно быть максимальное отталкивание электронов одного спина. Учитывая, что они же стягиваются к ядру атома, получается плотная упаковка - тетраэдр. Устойчивой оболочкой Линнет считал ориентацию двух тетраэдров, обеспечивающую их максимальное отталкивание, т.е. 4+4=8, куб. Пока мы не рассматриваем спин, его правило не отличается от правила октета, однако, оно приводит к геометрической трактовке связи. Например, отличие однократной, двойной и тройной связей выглядит так:

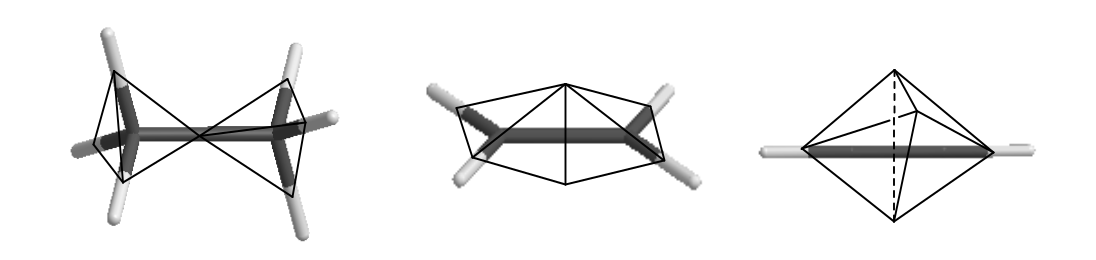
Этан, этилен, ацетилен.
Этан, этилен, ацетилен.

Интересно, что предсказываемые соотношения для длин связей находятся в прекрасном согласии с наблюдаемой геометрией молекул. Более того, его принцип позволяет объяснить электронную структуру молекулы кислорода, для которой основное состояние - триплет, два неспаренных электрона. Правило октета в данном случае бессильно.

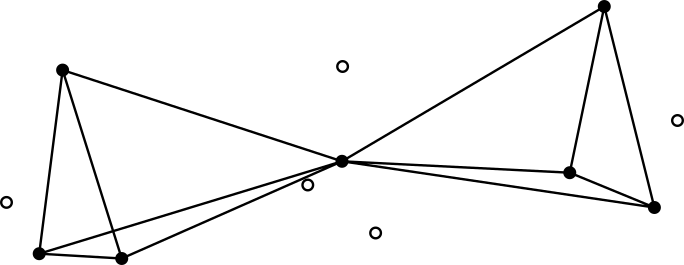
Триплетное состояние кислорода.
Триплетное состояние кислорода.

Долгое время было загадкой, почему две молекулы NO (свободные радикалы) не образуют устойчивый димер, в отличие от циана CN, который димеризуются в дициан C2N2. С позиции теории двойного квартета, структура O=N-N=O потребовала бы пространственного совмещения тетраэдров электронов разного спина, что невыгодно из-за электростатического отталкивания, тогда как дициан позволяет минимизировать отталкивание электронов. Принцип плотной упаковки электронов описывает все типы химических связей: ковалентную с кратными связями, ионную, а также металлическую связь.

Расчёт координат центроидов локализованных орбиталей Бойса у кислорода
! Используем программу GAMESS US
$CONTRL SCFTYP=UHF MULT=3
  LOCAL = BOYS
  RUNTYP=ENERGY NZVAR=0 
 $END
 
! PRTLOC = a flag to control supplemental printout.  The
!         extra output is the rotation matrix to the
!         localized orbitals, and, for the Boys method,
!         the orbital centroids, for the Ruedenberg
!         method, the coulomb and exchange matrices,
!         for the population method, atomic populations.
!         (default=.FALSE.)
 
 $LOCAL PRTLOC=.T. $END
 
 $SYSTEM TIMLIM=100 MWORDS=5 $END
 $BASIS  GBASIS=STO NGAUSS=3 $END
 $GUESS  GUESS=HUCKEL $END
 $DATA

 Cnv  4
 O   8.0  0.0  0.0  0.000
 O   8.0  0.0  0.0  1.210
 $END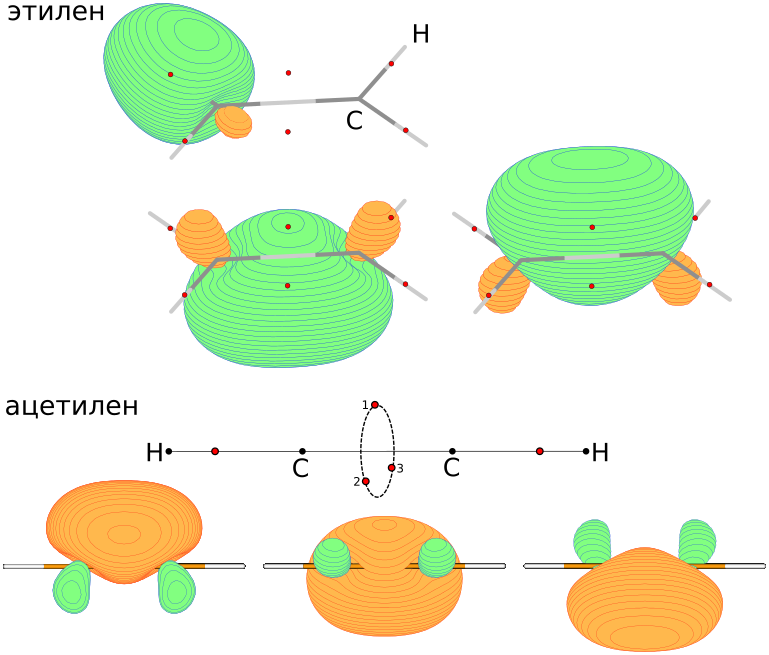
Орбитали Бойса. Связь C-H, двойная связь, тройная связь.
Орбитали Бойса. Связь C-H, двойная связь, тройная связь.

Орбитали Бойса, как видно из картинки выше, отличаются от "традиционных" представлений о различии связей ?-типа и ?-типа. Моё мнение - концепция Линнета куда как больше подходит к школьному курсу химии, чем существующий набор разрозненных представлений - правило Льюиса, гибридизация, орбитали... Электроны и ядра, связанные классическими механическими силами, выстраивают атомы и связи, последние, в свою очередь, образуют механическую молекулярную систему - появляется понятие о конформации молекул.

Потенциал Гейзенберга

Соотношение неопределённости \Delta x \cdot \Delta p \ge \hbar/2, как и принцип Паули, также интерпретируется с позиций механики. Рассмотрим атом водорода. Запишем импульс электрона - p, а радиус его орбиты - r. Имеем: p\cdot r \sim \hbar. Полная энергия атома (в системе атомных единиц):

E= \frac{p^2}{2m}-\frac{1}{r}

Тогда c учётом соотношения неопределенности p\cdot r = 1 имеем:

E(r)=\frac{1}{2r^2}-\frac{1}{r}

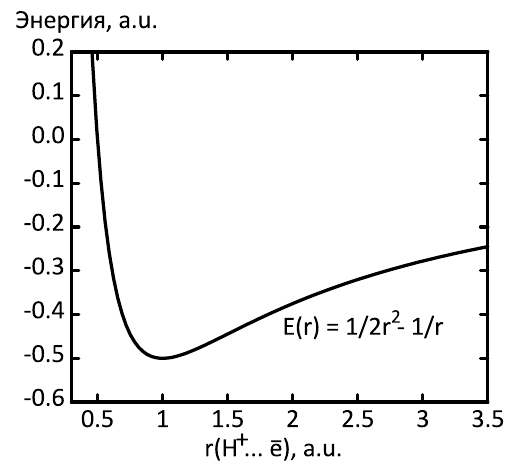
В точке минимума r=1 энергия атома водорода E=1/2 как и должно быть по законам квантовой механики. Вид потенциала аналогичен таковому у шарика на упругой пружинке. Воспользуемся найденным потенциалом для поиска кривой потенциальной энергии молекулярного ионаH_{2}^{+}.

Пусть электрон в молекулярном ионе H_{2}^{+} находится на линии связи H-H, на расстояниях от центров a, b. Тогда статическое равновесие сил записывается как:

\begin{align*} \frac{1}{a^{3}}-\frac{1}{a^{2}}-\frac{1}{b^{3}}+\frac{1}{b^{2}} & =0\\ a+b & =R \end{align*}

Решим систему уравнений и найдем зависимость полной энергии иона от межядерного расстояния.

Сессия MAXIMA решения системы уравнений.
Сессия MAXIMA решения системы уравнений.

Решение системы не требует каких-то нешкольных навыков, просто MAXIMA удобна, чтобы не запутаться в выкладках. Результаты на картинке ниже.

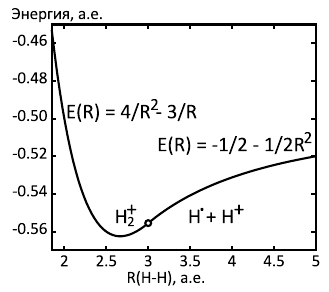
Кривая потенциальной энергии молекулярного иона водорода.
Кривая потенциальной энергии молекулярного иона водорода.

Мы видим, что молекулярный ион термодинамически стабилен относительно распада на протон и атом водорода. Энергия разрыва связи составляет 1/16 (164 кДж/моль), а длина связи - R=8/3 (1.41 A). Экспериментальные значения - 255 кДж/моль энергия связи, расстояние - 1.07 A. Для такой простой модели это более чем хорошее согласие.

Заключение

Сведение квантовомеханической задачи к молекулярной механике фермионов открывает в перспективе легкий и очень быстрый способ моделирования свойств материалов и химических реакций. Простые аппроксимации потенциалов Паули и Гейзенберга, к сожалению, не позволяют добиться высокой точности в предсказании свойств. Пока. Тем не менее, сам подход хорош уже тем, что не требует сложнейшего аппарата квантовой механики для понимания различных химических и физических явлений. Возможно, что кому то следующая мысль покажется крамолой, но я уверен в том, что основы химии можно объяснить без отсылок к квантовой физике. Без разбора уравнения Шредингера, гибридизации, теории резонанса, перекрывания орбиталей и прочего.

Наши серверы можно использовать для разработки и просчета научных экспериментов.

Зарегистрируйтесь по ссылке выше или кликнув на баннер и получите 10% скидку на первый месяц аренды сервера любой конфигурации!