Для некоторых физических объектов, подчиняющихся закону гравитации, сложение не всегда просто. Если объединить чёрную дыру массой 28 солнечных масс с чёрной дырой массой в 47 солнечных масс, полученная в результате чёрная дыра будет иметь массу 72 солнечные массы, а не 75. Фактически при слиянии любых двух чёрных дыр получаемая в результате масса меньше стартовой. Это связано не с недостатком математики, а скорее с особенностями работы гравитации. Здесь объясняется, почему при слиянии чёрных дыр всегда теряется масса.

Одно из первых научных правил, которым мы учимся в нашей жизни, — это сохранение энергии. Оно гласит, что энергия не может быть создана или уничтожена, а только преобразована из одной формы в другую. Поднимая тяжелый блок, вы выполняете работу (форма энергии) против силы тяжести: вы передаёте энергию блоку. В результате блок приобретает гравитационную потенциальную энергию. Если блок бросить, эта потенциальная энергия преобразуется в кинетическую энергию, а в момент соударения блока с полом эта энергия переходит во множество других форм: тепло, деформацию и звуковую энергию, помимо прочего.

Поэтому, если начать с двух масс, также присутствует определённое количество полной энергии, энергии, которая присуща всему, что имеет массу, и задаётся самым известным уравнением Эйнштейна: E = mc?. Есть, конечно, и другие формы энергии, но три из них нельзя игнорировать. Две из них более очевидны, чем третья; но мы должны рассмотреть все соответствующие формы энергии, если хотим убедиться, что всё, что необходимо сохранить, действительно сохранено.

В дополнение к энергии массы покоя мы должны рассмотреть энергию следующих трёх типов:

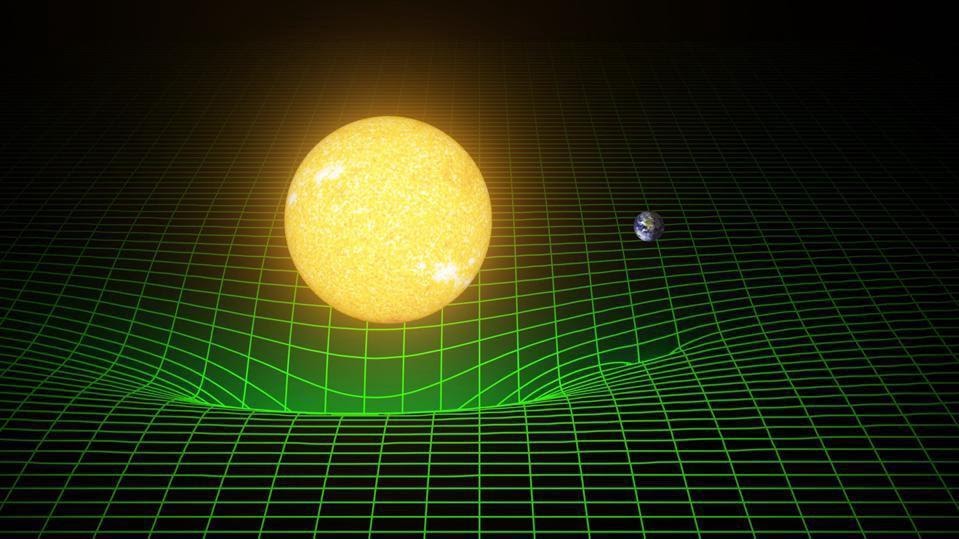
1. Гравитационная потенциальная энергия зависит от расстояния между двумя массами. Массы, разделённые бесконечным расстоянием, имеют нулевую гравитационную потенциальную энергию. Однако, чем ближе они друг к другу, тем больше «деформируется» пространство-время и, следовательно, тем больше мы получаем отрицательной гравитационной потенциальной энергии.

2. Кинетическая энергия определяется движением этих двух масс относительно друг друга. Чем быстрее вы двигаетесь, тем больше ваша кинетическая энергия. Сочетание кинетической и потенциальной энергии объясняет, почему «падающие» объекты ускоряются: по мере уменьшения отрицательной гравитационной потенциальной энергии растёт положительная кинетическая энергия.

3. Энергия также содержится в гравитационных волнах (форма гравитационного излучения, которая уносит энергию из системы).

В то время как понятия энергии массы покоя, потенциальной гравитационной энергии и кинетической энергии прекрасно работают в ньютоновской механике и гравитации, гравитационное излучение по своей сути — новая идея, присущая общей теории относительности Эйнштейна. Когда массивное тело движется через область пространства, в которой изменяется кривизна пространства-времени или ускоряется массивное тело (меняет направление), даже когда кривизна пространства-времени остаётся постоянной, такое взаимодействие порождает излучение определённого типа — гравитационные волны.

Любое массивное тело, вращающееся вокруг любого другого массивного тела, будет излучать эти волны, причём, как правило, чем меньше масса, тем больше эффект. Например, мы считаем, что Земля вращается вокруг Солнца по стабильной орбите, но технически это не совсем верно. Если бы свойства Солнце оставались постоянными — никаких изменений массы никогда, — Земля не осталась бы на эллиптической орбите навечно. Наоборот, планеты будут медленно излучать энергию, их орбиты будут снижаться, и в конечном счёте они будут по спирали приближаться к Солнцу. Для достижения финальной точки Земле может потребоваться около 10?? лет. Падение остаётся ненаблюдаемым долгое время, но, если гравитационное излучение реально, то оно произойдёт.

Однако во многих астрофизических сценариях эффекты гравитационных волн гораздо более выражены. В общем, любой эффект, который существует только в общей теории относительности (а не в ньютоновской гравитации), будет самым сильным там, где:

• массы велики;

• расстояния малы;

• кривизна пространства велика.

Где у нас есть большие массы на малых расстояниях, где пространственная кривизна очень значительна? Вблизи массивных, компактных объектов: белых карликов, нейтронных звезд и чёрных дыр. Из всех них у чёрных дыр наибольшие массы, наименьшие объёмы, к ним можно подойти на очень близкое расстояние, и рядом с ними пространственная кривизна максимальна.

Однако чёрные дыры чрезвычайно трудно обнаружить и наблюдать, в то время как многие нейтронные звёзды имеют характерный признак — очень регулярную пульсацию. Когда одна пульсирующая нейтронная звезда вращается вокруг другой, большей массы, например другой нейтронной звезды или чёрной дыры,  мы можем начать измерять поведение таких импульсов, и они открывают нам нечто захватывающее.

Если бы нейтронная звезда находилась на совершенно стабильной орбите, которая никак не деформируется из-за излучения предсказанных гравитационных волн, мы получили бы постоянный во времени характер импульсов. Однако, если бы орбита распадалась, мы бы увидели эволюцию этого характера импульсов, и, в частности, мы также увидели бы ускорение самого орбитального движения. (С потерей энергии тело падает ближе к другим массам, а это означает более плотные и быстрые орбиты.)

С 1960-х годов мы знаем о двойных пульсарах, т. е. пульсарах, вращающихся вокруг другой нейтронной звезды. Мы также знаем о «синглетных» пульсарах, или пульсарах, которые в своей системе представляют собой единственное тело с большой массой. Что мы обнаруживаем при длительном наблюдении за такими объектами? У таких пульсаров очень последовательный характер импульсов, и этот характер не изменяется с течением времени. Однако для двойных пульсаров характерно не только изменение последовательности наблюдаемых импульсов, но и сама последовательность меняется в точности так, как предсказывает общая теория относительности в силу излучения гравитационных волн.

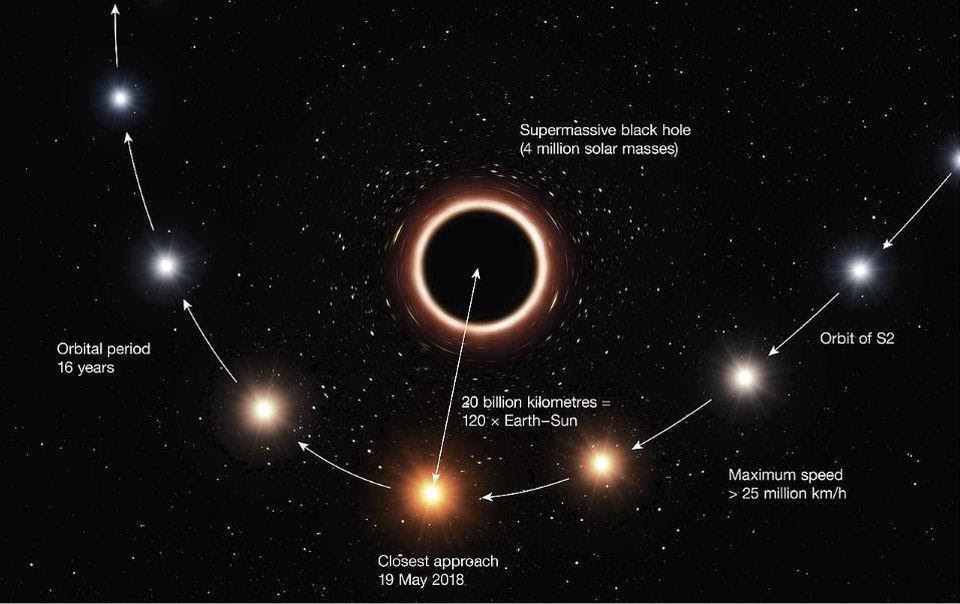
Па-де-де в космосе: когда две нейтронные звезды танцуют вокруг общего центра гравитации, они излучают гравитационные волны. Поскольку это происходит с обоими объектами, они теряют часть орбитальной энергии, медленно приближаясь друг к другу по спиральной орбите, а их период обращения становится всё короче. Диаграмма справа показывает их состояние как двойного пульсара PSR-J0737-3039.

Хотя нейтронные звёзды могут быть как массивными, так и невероятно компактными, достигая по массе чуть более 2 солнечных масс при размерах всего 10–20 километров, чёрные дыры ещё экстремальнее. Их массивные тела сжимаются до сингулярности, скрытой за горизонтом событий (граница, из-за которой теоретически ничто не может вырваться), размер и форма которого определяются только их массой и угловым моментом.

Когда чёрные дыры вращаются друг вокруг друга в так называемой двойной системе чёрных дыр, каждая масса испытывает влияние пространства-времени, искривлённого другой массой. Когда они движутся по взаимным орбитам, взаимодействие массы и искривлённого пространства-времени порождает излучение. (Аналогичный эффект имеет место в электромагнетизме, когда заряжённая частица, движущаяся/ускоряющаяся через изменяющееся электромагнитное поле, испускает излучение.) Амплитуда, частота и энергия гравитационного излучения определяются величиной масс, разделением масс и скоростью движения масс в этом искривлённом пространстве-времени.

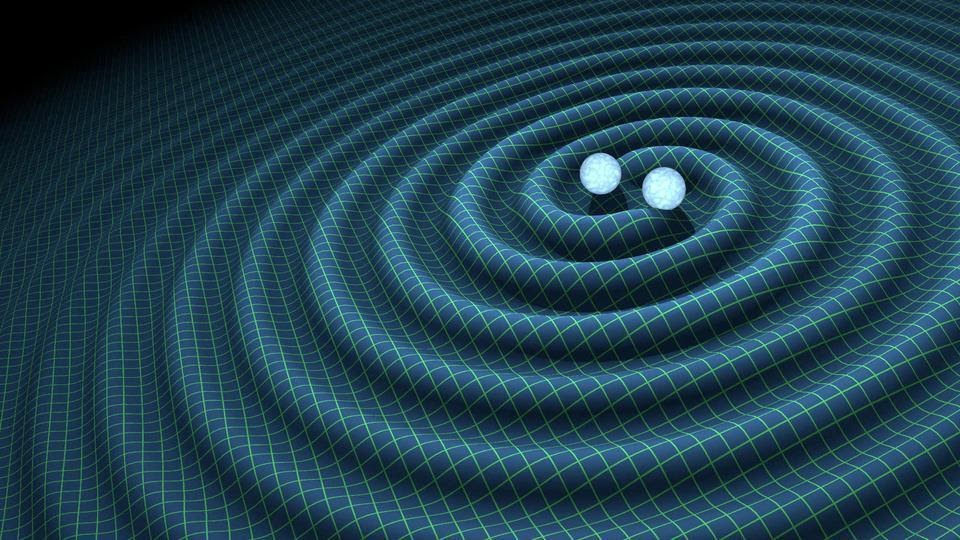
Удивительно то, что большая часть излучаемой энергии — около 90 % или более — испускается только во время последних двух или трёх орбитальных витков этих масс друг вокруг друга, а также в момент самого слияния. Если бы не этот энергетический пик в самом конце долгого космического танца, мы бы полностью пропустили многие события излучения гравитационных волн, которые мы видели, включая самое первое.

Во многих случаях только всплеск во время этих последних миллисекунд даёт нам верную сигнатуру сигнала гравитационных волн, возвышающегося над шумом. (Также часто удаётся извлечь оставшийся сигнал.) Во многих отношениях мы наблюдаем самые энергетические события излучения гравитационных волн со времён Большого взрыва. Например, за последние несколько миллисекунд, когда горстка солнечных масс может быть преобразована в энергию гравитационных волн, при слиянии система двух чёрных дыр может излучать больше энергии, чем все звёзды во Вселенной, вместе взятые.

Забавно в этом то, что есть простое приближение, которое позволяет ответить на вопрос: «При слиянии любых двух чёрных дыр какая часть массы преобразуется в энергию?»

Приближение? Просто возьмите меньшую массу из двух сливающихся чёрных дыр, умножьте это значение на 0,1 — примерно такая часть массы преобразуется в энергию. Да, это 10 % от массы меньшей чёрной дыры.

Существуют всевозможные сложные эффекты, и большая вращательная составляющая чёрной дыры, которая есть у многих из них, может немного изменить историю. Однако эффекты масс, как правило, доминируют над спином / угловым моментом, а эффекты неравномерных соотношений масс, как правило, невелики. Фактически физик Виджай Варма построил график в целях проверки этого приближения для различных соотношений масс, и, как вы видите, «10 % от меньшей массы» — отличное приближение для доли массы, которая преобразуется в энергию при слиянии двух чёрных дыр.

Если происходит слияние двух чёрных дыр и известны их начальные массы, можно предсказать, какая часть этих масс перейдёт в окончательную чёрную дыру после слияния, а какая часть будет излучена в виде гравитационных волн. Просто возьмите чёрную дыру меньшей массы, уберите из неё 10 % массы, а чтобы получить конечный результат, оставшуюся часть объедините с другой чёрной дырой. Между тем эти «10 % массы меньшей чёрной дыры» преобразуются в гравитационные волны, которые распространяются по Вселенной во всех направлениях.

Таким образом, если взять чёрные дыры массой 46 и 40 солнечных масс, масса конечной чёрной дыры равна 82 солнечным массам, а 4 солнечных массы будут излучены.

Для чёрных дыр массой 53 и 10 солнечных масс масса финальной чёрной дыры равна 62 солнечным массам, а в излучение перейдёт 1 солнечная масса.

Для чёрных дыр массой 47 и 28 солнечных масс масса финальной чёрной дыры равна 72,2 солнечной массы, а в излучение перейдёт 2,8 солнечной массы.

Пока пространство искривлено, массивное тело не может двигаться через него, не испуская гравитационного излучения. В самых тяжёлых случаях это даже влияет на то, как выполняется сложение. От первого предсказания гравитационных волн до их первого прямого измерения прошло 100 лет, и это достижение никогда не выглядело более впечатляющим. По мере улучшения наших наблюдений мы сможем выявить более тонкие эффекты, наложенные поверх этого простого приближения. Однако пока наслаждайтесь простотой математики чёрных дыр, которая доступна каждому!

Несмотря на такую простоту математики столкновений чёрных дыр современное моделирование космических процессов по-прежнему требует анализа огромных потоков данных с детекторов, иными словами, до подобных упрощений и допущений нужно доходить ощутимо трудными путями, зато результаты трудов всегда будут поражать нас красотой, точностью и чёткостью науки.

Сегодня анализ данных и работа с ними — отдельная, интересная область не только в науке, но и в сфере бизнеса — пренебрегать данными сейчас просто невозможно. И если область работы над данными и их анализа вам интересна, вы можете обратить внимание на наш флагманский курс по Data Science, где получаемый студентами объём знаний равен знаниям, приобретаемым за два-три года активного самостоятельного изучения науки о данных.

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:

• Профессия Data Scientist

• Профессия Data Analyst

• Курс по Data Engineering