Введение

Возможно ли превратить координаты на изображении в конкретные географические координаты? Несмотря на то, что это звучит несколько необычно, такая конвертация вполне возможна.

Сегодня я расскажу о том, как можно спроецировать координаты с плоского изображения на карту. Эта короткая статья будет своеобразным продолжением первой статьи, в которой я рассказывал о базовых возможностях Mask R-CNN.

Статья была написана в сотрудничестве с @avdosev за что ему большое спасибо.

Проблема

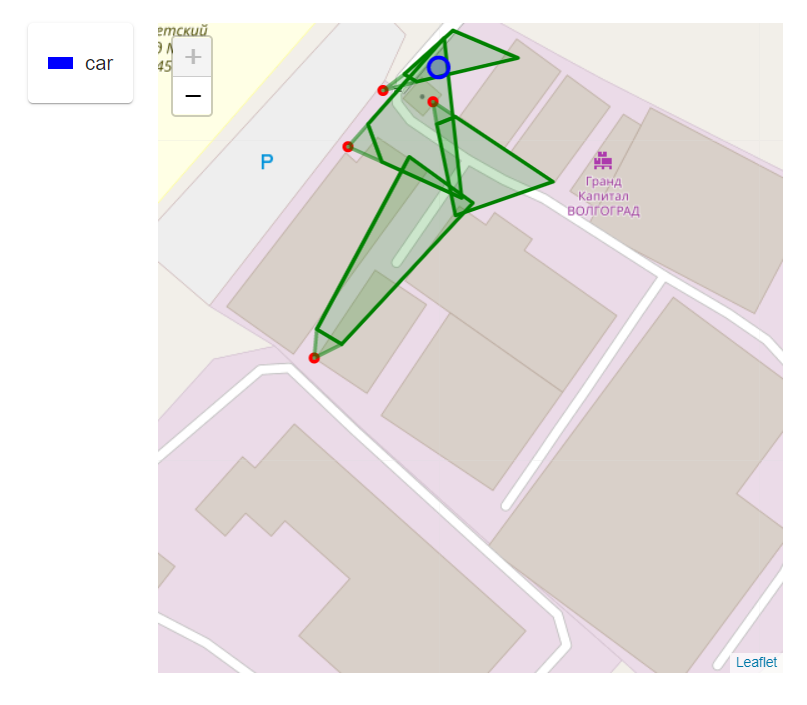
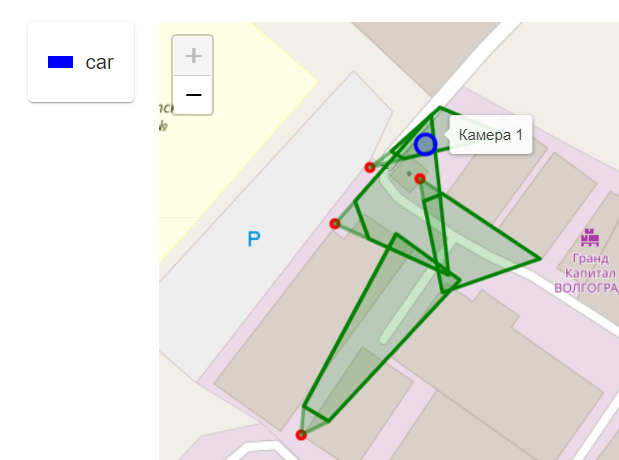
Необходимо по изображению с камеры понять, где находится объект на карте территории. Схематично это выглядит так.

На изображении каждый объект у меня вписан в прямоугольник, это не случайно, в дальнейшем мы будем с помощью этого прямоугольника получать нужный пиксель для объекта.

Также условимся, что мы рассматриваем простой случай, когда камера не пересекает стены, и мы можем представить ее область видимости при виде сверху, как трапецию.

Требования к камере:

• Не должно быть рыбьего глаза.

Требование к изображению:

• На изображении с камеры должна быть видна плоскость земли.

Способ 1

Можно задать для каждого пикселя изображения соответствующую координату местности. При необходимости узнать геокоординату, мы просто ее получим по связанному пикселю.

Достоинства:

• Алгоритм будет работать быстро, мы ограничены скоростью доступа к Map структуре данных, файлу или базе данных;

• Сложных вычислений в рантайме нет.

Недостатки:

• Если камера сдвигается даже на миллиметр, все наши данные устаревают, и будут давать уже не точный результат;

• Требуется хранить информацию о каждом пикселе для каждой камеры на территории, что нецелесообразно;

• Задавать для каждого пикселя координаты слишком долго и сложно.

Исходя из этих проблем, был отброшен первый способ и продолжен поиск других.

Способ 2

Имея координаты углов области видимости камеры, можно вычислять координаты для подаваемого пикселя. Их можно получить двумя способами:

1. Посмотреть на карту территории и изображения с камеры и постараться указать наиболее точные координаты углов;

2. Зная параметры камеры (высота над землей, координаты камеры, угол наклона камеры и углы обзора), получить координаты углов видимости (трапеции), либо сразу вычислить координаты объекта.

Расчет положения объекта по координатам углов видимости

Для начала стоит разобраться, как выглядит область видимости камеры на виде сверху. 

Для работы с этой областью, нужно отбросить часть плоского конуса рядом с камерой, которую я обозначил красным на рисунке выше. Эта область выбирается, исходя из того, что в красную зону не могут (или не должны) попасть объекты.

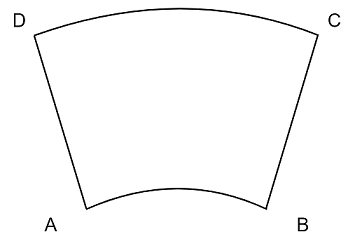
Для простоты расчетов можно считать его трапецией.

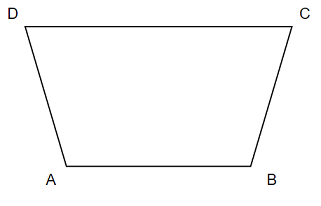
Для расчета местоположения объекта используем следующие формулы.

Где

•  l2 , l1 – промежуточные переменные для вершины;

• imageHeight, imageWidth – высота и ширина изображения с камеры в пикселях соответственно;

• A, B, C, D – географические координаты вершин трапеции поля зрения камеры в формате {lat: float, lng: float};

• X, Y – координаты пикселей на изображении в декартовой системе координат, являются целыми числами;

• M - результирующие координаты.

В случае Full HD картинки ширина и высота будут следующими: imageHeight=1080; imageWidth=1920.

После распознавания объекта на изображении, нейросеть отдаст координаты углов прямоугольника. Из него необходимо выбрать точку на изображении, для которой будут определяться координаты. Для этого есть несколько способов:

1. Брать центроид прямоугольника;

2. Брать середину нижней стороны прямоугольника. Этот способ даст более точный результат, если объект перемещается по земле, а не летает;

Всё это можно объединить:

Взять 1/N высоты и центр по горизонтали, где N может изменяться в зависимости от различных факторов, например, типа объекта или способа перемещения.

Например, для N=8 мы получим такую результирующую точку на прямоугольнике объекта.

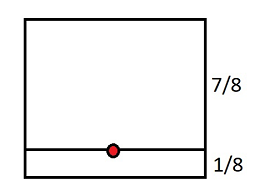
Все эти способы имеют существенную погрешность при малой высоте камеры или/и при большом наклоне камеры. 

Расчет углов видимости камеры, используя ее характеристики 

Для нахождения точек A, B, C, D автоматизированным образом, нам необходимо найти центр будущей трапеции C.

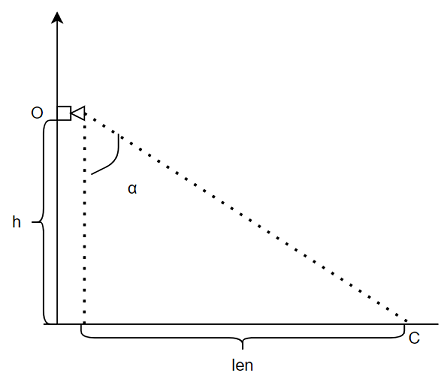
Зная высоту h и угол наклона камеры ?, мы можем найти противоположный катет len.

Зная координаты камеры (точка О) и её направление (в какую сторону она смотрит, угол ?) можно найти центр её наблюдения (точка С). Найти ее можно по формуле:

Измерить угол ? и ? на практике может быть затруднительным. Чтобы избежать сложных замеров, можно оценить примерную координату точки C (центр изображения), и вычислить углы.

Для того, чтобы найти координаты углов изображения, необходимо знать углы обзора камеры по горизонтали и вертикали. Посмотрев углы обзора в характеристиках камеры, мы можем найти координаты. Расчеты выполняются аналогично расчету центральной точки. При этом необходимо делать смещение.

Для основного угла ? +/- половина угла обзора по вертикали.

Для вторичного угла ? +/- половина угла обзора по горизонтали.

Примем горизонтальный угол обзора за viewAngleHorizontal, а вертикальный за viewAngleVertical.

Для точек, которые находятся ближе к камере, мы отнимем половину угла обзора, а для дальних - добавим.

Далее повторно рассмотрим точки трапеции. (Не стоит путать следующую точку C с центральной).

Скомбинировав смещения по углам обзора, мы получаем координаты углов изображения - точки A, B, C, D.

Зная точки A, B, C, D можно получить географические координаты объекта. Но можно обойтись и без них. Следующий расчет потребует imageHeight, imageWidth, X, Y.

Если добавить вспомогательные оси, где координаты X, Y будут центром, то наш пиксель поделит изображение на 4 части. Определив отношения частей по горизонтали и по вертикали, мы можем определить углы, на которые должны делать смещение. Итоговая формула выглядит так:

Реализация на Python

imageWidth = 1920 # в данном примере зададим их константами
imageHeight = 1080

import numpy as np

def geoToList(latlon):
  return np.array((latlon['lat'], latlon['lng']))
  
def listToGeo(latlon):
  return {'lat': latlon[0], 'lng': latlon[1] }
  
def getGeoCoordinates(A, B, C, D, X, Y):    
  A, B, C, D = list(map(geoToList, [A, B, C, D]))    
  vBC = (C - B) / imageHeight    
  vAD = (D - A) / imageHeight    
  latlonPixel1 = vBC * (imageHeight - Y) + B    
  latlonPixel2 = vAD * (imageHeight - Y) + A    
  vM = (latlonPixel2 - latlonPixel1) / imageWidth    
  M = vM * X + latlonPixel1    
  return listToGeo(M)

Результаты

Из этого изображения были получены координаты объекты левого верхнего и правого нижнего угла по X, Y соответственно - 613;233 1601;708.

Исходный код всегда доступен на Github.

Если найдете ошибки в алгоритме или в формулах, пожалуйста, сообщите об этом в комментариях.

Литература

• Using Calibration to Translate Video Data to the Real World

• Using panoramic videos for multi-person localization and tracking in a 3D panoramic coordinate