It is an efficient searching technique. Searching is a widespread operation on any data structure. Hashing is used to search specific records from a large domain of records. If we can efficiently search a record out of many records, we easily perform different operations on that data. Hashing is storing and retrieving data from the database in the order of O(1) time. We can also call it the mapping technique because we try to map smaller values into larger values by using hashing.
Following are the significant terminologies related to hashing
Search Key
In the database, we usually perform searching with the help of some keys. These keys are called search keys. If we take the student data, then we search by some registration number. This registration number is a search key. We have to put the search keys in hash tables.
Hash Table
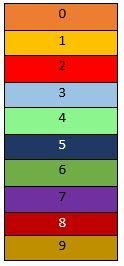
It is a data structure that provides us the methodology to store data properly. A hash table is shown below. It is similar to an array. And we have indexes in it also like an array.
Hash Function
When we perform searching, inserting, or deleting some data from it, we don’t need to scan the whole table. With the help of a hash function, we will perform it with the order of O(1) time. There are different hash functions such as:
K mod 10
K mod n
Mid Square
Folding Method
‘K mod 10’ and ‘K mod n’ are the most widely used methods.
Suppose we have a number 24 and hash function ‘K mod 10’.With the help of the hash function, we will map 24 in the hash table. For this purpose, we can put K is equal to 24 so:
24 mod 10 = 4
So we can place 24 at index 4 in the hash table. Then for 52 number
52 mod 10 = 2
52 will go to index 2 location. Next for number 91
91 mod 10 = 1
So, 91 will be placed at index 1 in the table. Then finally for 67
67 mod 10 = 7

A hash table uses two components:
Hash function
Bucket Array
For an element key pair, the hash function calculates some value based on a key. A hash function is a function with a key as an input parameter. A hash function will give us two parts:
Hash Codes
In this, we assign an integer to the key. It is going to map the key to some integer.
Compression Map
It will convert the integer, or rather it will map the integer which we have received from the hash code to an integer in the range 0 to n-1. Once we have the hash function of the key, we would first receive an integer, and then map that integer to 0 to n-1. So the outcome of the hash code or the outcome of the hash function will be an integer in the range 0 to the n-1. This integer depends on the key of the input element.
In the bucket array, we are going to store the element in an array of hash functions of the key. So once we will receive an integer in the range 0 to n minus 1.So, we will store the element in an array of not just the key but the array of hash function of the key. So, once we do this, the keys no longer have to be integers. Also, we don’t need to know the range of keys because we are going to map it into a range which is provided by us.
Hash Code
Hash code is a function that converts a key to an integer. So it's going to convert a key of any type to an integer.
Following are some properties of a good hash code:
It will minimize collisions. It means that if we are given two keys that are different, their hash codes should also be different. So if two keys say ‘K1’ does not equal ‘K2’.
K1 ≠K2
It implies that the hash code of key 1 should also not equal to the hash code of key 2.If two keys are a map to the same hash code, then we say a collision has occurred. We don’t want this. We want different hash codes for different keys. So we want to minimize collisions.
A good hashcode should be uniform. If we have a key ‘K1’ and that is equal to key ‘K2’.
K1 = K2
Then we don’t need different answers for hash code. Because for the same value of the key, if we run our hash code, then we should always get the same value of the hash code. So if both keys are equal, then the hash code of Key 1 has to equal the hash code of Key 2.
hash(K1) = hash(K2)
Hash Code Map Example
Memory Address
In this, we are going to interpret the memory address of the key as the hash code. So we are going to take the memory address of the key as the hash code of the key.
Let's take an example of it. We have a key 1, and this is at a memory address of 5000. Then we have key 2, and this is at memory address 5010.

Hash(K1) = 5000
Hash(K2) = 5010
It can be seen that the key, whatever the data type it may be, has arrived at an integer that maps to that data.
Disadvantage
The disadvantage of this hash code is that this is not uniform.
Integer Cast
It is a method of mapping to an integer. In this, whatever the data type of the key may be, typecast it to an integer. So if we have a string and we typecast a character of that string, it is going to return an ASCII value to us. And thereby, we will get an integer.
Disadvantage
Its disadvantage is that for data types like double or float, we encounter a loss of data. And a lot of collisions will occur in this method.
Component Sum
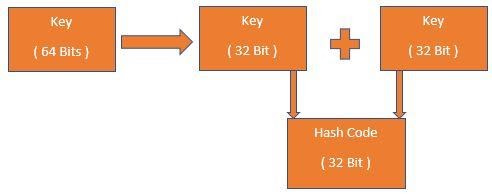
It is a type of hash code in which the partition bits of the key into fixed-length components. Suppose we have a float or a double that’s going to be 64 bits for us. We will partition them into a fixed bit component. So we will partition these 64 bits into two 32 bits. Then we will add these two 32 bits to get a 32-bit hash code after ignoring overflow.
Suppose we use a string case. And We have a key that is equal to the string ‘NAME’. So, in this case, we will not directly typecast this to an integer. We will divide this into four 32 bit segments. Then we will add these values. For each of these values, we take ASCII values of each of these characters. Then we will get the final hash code by adding each of these values.
Key = ‘NAME’
ASC(N) + ASC(A) + ASC(M) + ASC(E)
Hash Code (Key) = X
Disadvantage
Its disadvantage is that a lot of collisions can occur with different arrangements of various segments.
Polynomial Accumulation
In this, firstly, we divide a key into different segments like component sum. But in polynomial accumulation, we just take some variables or integers or some non-zero constant.
Suppose we have a key that is equal to a string ‘CODE’. We will divide this key into 32-bit segments. Then we will take the ASCII value of each of the string characters. Then we will take the sum of ASCII of each character into non-zero constant ( a ).
Key = ‘CODE’
( ASC(C) x a0 )+( ASC(O) x a1) + (ASC(D) x a2) + (ASC(E) x a3)
Hash Code (Key, a)
In this, if we change the arrangement of letters, the hash code is also going to change. For the same keys, we will get the same hash code. For the different keys, we will get different hash codes. Now let's take a look at the program of hash code. Let's say that key is going to be an array. Elements of this array will contain 32-bit segments which we have divided our key into. At position 0, we will have ASCII of ‘C’. At position 1,2, and 3, we will have ASCII of ‘O’,’D’, and ‘E’. Now program to calculate the hash code is:
for(i= n-1 ; i > = 0 ; i--){
sum = ( sum * a ) + arr[i];
}
arr[ C , O , D , E ]
i = 3 , sum = E ;
i = 2 , sum = Ea + D ;
i = 1 , sum = Ea2+ Da + O;
i = 0 , sum = Ea3+ Da2+ Oa + C;Hashing Techniques to Resolve Collision
When we calculate some hash function or location or address for keys and use that same hash function. That hash function will give the same index, but we cannot store two values at the same place in the hash table. This process is called a collision. To resolve these collisions, we have some techniques:

Separate Chaining
In this type, if two keys hash to the same hash value, then in the bucket array for that particular hash value index, we will create a linked list.
Let's consider we have keys 100,105,200, and 205. Hash function is equal to K times mod of 10.
Keys = 100 ,105,200,205
H(K) = K mod 10
Since the range of this function is 10, we have a bucket array of elements ranging from 0 to 9. For the first key-value, which is 100, 100 mod 10 is equal to 0. So it will be filled at index 0. At index 0, we will start a linked list with the key of 100. Now for key 105,
105 mod 10 = 5
So now start a linked list with a key of 105 at index 5.Then, for key 200,
200 mod 10 = 0
So we will go to the index 0 and add it to the end of the linked list after 100. Now for the key 205,
205 mod 10 = 5
We will go to index 5 and add it to the end of the linked list after 105. This is how to separate chaining works.

So we always need two functions for a hash table in it. The first insert operation and the second is the search operation. Let's look at the algorithm of each function.
Insert
This algorithm is fairly simple. If we say insert and we have an algorithm ‘insert item' . And we have a (key, element) pair which we want to insert. So, we will go to the index, which is equal to the key. Then at that index, we will have a linked list. This is going to be an array of linked list.So to this linked list, we will insert at the end the key-element pair.
Search
If we want to search for a key-element pair, the linked list we search for the element will be equal to the linked present in the array of the index key. So call this linked as C and store the array of a key in it. Now C is a linked list in which we want to search.
Linear Probing
In this, when a collision occurs, that is two distinct keys are mapped to the same hash value. In such a case, the colliding element will be positioned in the later circularly available table cell.
To understand the working of linear probing, let's consider that our hash function is:
H(x) = x mod 10
And keys are:
Keys = (18,41,22,32,44,59,79)
Now hash values will be:
Hash Values = ( 8, 1,2,2,4,9,9)
As the range is 10, the bucket array will have indexes from 0 to 9. We will place each key in the index, which is equal to their hash value. For the key value 32, its index value is the same as key-value 22. Index 2 has been already filled with key 22, so I will check its next index. As next index 3 is empty or free, so key 32 will be placed here. The index for key 79 is 9, but it has already been filled with key 59 because its index is also 9. So, we will go to the next circularly available table cell, which is 0. As index 0 is free, so we will place key 79 here:

Now let's see the pseudocode for inserting an element. Firstly we will calculate the hash code or hash value of the key and store that value in variable ‘H’. The key could be either placed at index H or could be placed at an index somewhere different from H provided that H is not empty. So let's keep the incrementing variable i equal to 0.
Quadratic Probing
In linear probing, a lot of elements start clustering. That is, elements will start to be stored in groups or in a group of consecutive filled cells. This is not good because when we want to add an element to a cluster , we have to probe through many indexes to finally add that element. So it is not very time efficient. The solution to this problem is quadratic probing. In quadratic probing, we have to check which indexes to check when we want to add an element. We iteratively check the index of the hash value of the key plus square of i mod N.The expression for quadratic probing is:

Suppose we have a hash function:
H(x) = x mod 10
And keys are:
Keys = ( 2, 12 , 22 )
Hash value will be:
Hash = ( 2,2,2 )
Now we will create an array having indexes 0 to 9.Firstly, key 2 will be placed at index value 2 in the array. Key 12 has index value 2, but index 2 has already filled with key 2.So to place key 12, the index value will be:
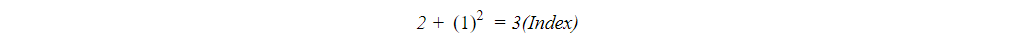
Now key 22 has index value 2, but it has been already filled, so we will find their index values as:


Double Hashing
In double hashing, we check iteratively indexes of the hash value of K plus j into the hash value of 2K.
Double Hashing = Hash1(K) + j Hash 2(K)
We have two hash functions in double hashing. In the above expression, ‘j’ is the iterative element starting at 0.
The values of both hash functions will be:

Now we will create a bucket array from 0 to 12 index value because the maximum range of N is 13. Now we will insert these hash values into the bucket array.
For adding key value 18:
5 + (0*3) = 5
So 18 will go to the index value 5.
For key value 41:
2+ (0*1)=2
Similarly for keys 22 and 44:
9+ (0*6) = 9
5+(0*5) = 5
Keys 22 will go to index value 9 but key 44 has index value 5 which is not empty. So now we will take:
5+(1*5) = 10
So the index value for key 44 will be 10.