ЧАСТЬ  ВТОРАЯ: Нитка с иголкой в ткани энергии.

Мы продолжаем изучать волшебство преобразования энергии в ШИМ преобразователе. Почему волшебство? Теоретически, как мы убедились в предыдущей части, линейный стабилизатор, изначально по природе своей, переводит часть полезной энергии в тепло, делая КПД линейного стабилизатора менее 100%, что в принципе ожидаемо для технических систем. А в ШИМ преобразователе, теоретически, это происходит без потерь, ну чем не волшебство? ШИМ преобразователь, словно портной ножницами, нарезает своими ключами ткань энергии на лоскутки, а потом как швейная машинка сшивает фильтром лоскутки энергии в стройное платье - постоянную составляющую (ПС). 

Что такое ПС и как её получить? Давайте изучим!

Широтно-импульсно модулированный Сигнал - лоскутки Энергии.

Как было сказано в прошлой части, с помощью ключей, энергию можно нарезать порциями в виде прямоугольных импульсов, обладающих новыми качествами и характеристиками, которые можно, а самое главное, нужно понимать для эффективного применения их свойств, целью которых является получение постоянной составляющей (ПС) из ШИМ Сигнала. 

Рассмотрим несимметричный периодический прямоугольный сигнал относительно горизонтальной оси:

Где:

Am - Амплитуда импульсов Сигнала

Т - период Сигнала

tw - длительность импульса, именно меняя ее, т.е. ширину импульсов, без изменения T, модулируется Сигнал - отсюда и название ШИРОТНО-ИМПУЛЬСНАЯ МОДУЛЯЦИЯ - ШИМ.

 Отношение ширины импульса tw к его периоду T называют коэффициентом заполнения D (от англ. Duty cycle), а величина, обратная ему называется скважностью S:

D = 1/S = tw/T

На практике для Сигнала одной и той же частоты удобнее пользоваться коэффициентом заполнения, который зачастую выражают в процентах умножая D на 100.

Т.к. Сигнал прямоугольный и несимметричный, то D напрямую влияет на его ПС, и поэтому находится в жесткой линейной зависимости от D и амплитуды (Am):

ПС = Am * D

Как раз именно это важное полезное свойство применяется на практике и позволяет использовать ключевой режим работы РЭ при применении ШИМ для нашей главной! цели: получение ПС из прямоугольного Сигнала.

Изучим как работает ШИМ, для чего создадим схему “PWM Generator work”:

V1 - источник постоянного напряжения, который в данном случае будет задавать D в диапазоне от 0 до 1В (0-100%), установим его значение равное 250мВ (т.е. 25%).

U1 представляет из себя программируемый генератор ШИМ Сигнала (название в библиотеке: PWM Generator), выходной сигнал которого, представляет из себя прямоугольные импульсы следующие с заданной частотой, при этом ширина импульсов линейно зависит от входного напряжения V1 (цепь Vin), которая и определяет значение D.

 Настраиваемые параметры ШИМ генератора следующие:

• Диапазон входного (программируемого) напряжения Vin должен находиться в диапазоне от MODLOW (соответствует 0%) до MODHIGH (соответствует 100%);

• Частота выходных импульсов MODFREQ ;

• Амплитуда импульсов на выходе Vout. Минимальное значение: PWMLOW, Максимальное значение: PWMHIGH.

Ширина импульсов tw автоматически рассчитывается внутри симулятора в соответствии с формулой:

WIDTH= Vin / ( (MODHIGH - MODLOW ) * MODFREQ )

Настроим U1 для удобства расчетов:

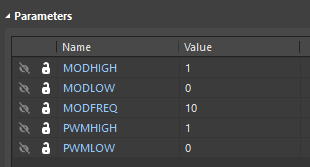
На вход U1 с V1 подается постоянное напряжение 0,25В (D=25%), что в соответствии с формулой, ширина импульсов должна быть 25 мс. 

Теперь давайте посмотрим, что получилось на выходе. В данном случае нам необходимо посмотреть Cигнал во временной области, в Симуляторе это нам позволяет сделать следующий вид анализа: Transient (виртуальный осциллограф), который мы и настроим: отобразим сигнал Vout на временном промежутке от 0 до 200 мс, с шагом 100 мкс.

Запускаем расчет Transient (RUN), Смотрим график и убеждаемся в правильности формулы и работы модели электрической цепи:

Глядя на Cигнал, мы видим присутствие ПС, значение которой можно вычислить на калькуляторе, но это будет не полная информация о сигнале, т.к. сигнал состоит не только из одной ПС, но еще из целого ряда гармоник, (ряд гармоник одного Сигнала называется - Спектр Сигнал

а), которые при практическом применении необходимо учитывать, а для этого нам необходимо знать их точный состав. Оказывается, что в Симуляторе есть еще один прекрасный инструмент, который позволяет быстро показать Спектр Сигнала - “преобразование Фурье” (Fourier Analysis), который находится внутри анализа Transient и активируется установкой соответствующего флажка Fourier Analysis во вкладке Transient:

У Fourier Analysis есть две настройки:

• Fundamental Frequency - этим параметром мы подсказываем симулятору периодичность раскладываемого сигнала, в нашем случае это 10Гц;

• Number of Harmonics - какое количество гармоник мы хотим видеть на графике спектра.

После настройки Fourier Analysis еще раз запускаем Transient и рядом с окном Transient появится окно Fourier Analysis:

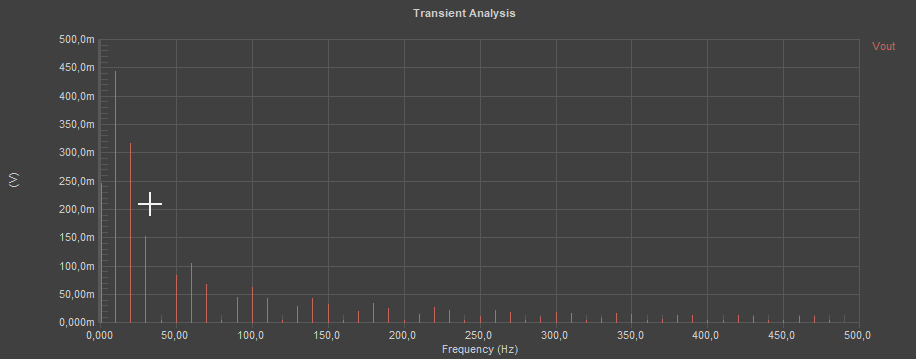
Посмотрите, на нулевой частоте вертикальная красная линия равна 250 мВ, это и есть ПС, которую мы задали в самом начале, а правее от нее остальные составляющие спектра. Давайте посмотрим Сигнал и его спектр противоположного случая, при D=75% (V1=750 мВ), ширина импульса должна быть 75 мс и соответственно ПС должна быть равна 750 мВ:

Сравните внимательно спектры, ПС изменилась с 250 мВ на 750 мВ, а вот остальные спектральные составляющие не изменились в принципе.

Таким образом, для решения задачи преобразования энергии, как было сказано ранее, нас интересует только ПС, а значит надо отфильтровать ее от ВСЕХ ненулевых спектральных составляющих и это можно сделать только с помощью Фильтра Низких Частот (ФНЧ). 

1.5 Фильтр Низких Частот (ФНЧ) - удивительная швейная машинка

Как иголка в руках портнихи, так фильтр в преобразователе вышивает нить из полотна энергии...

ФНЧ можно реализовать двумя базовыми способами: 

1. с помощью RC интегрирующей цепи - данный способ широко применяют, где требуется выделить ПС в качестве информации, и не подходит для преобразования энергии, т.к. на R будет рассеиваться (т.е. попросту теряться) энергия в виде тепла, что нас категорически не устраивает для текущей задачи;

2. с помощью LC цепи - в данной цепи нет ЭК на котором происходит выделение тепла, а значит и потерь,  именно эта цепь и используется для преобразования энергии, которую сейчас и рассмотрим.

Создадим следующую схему фильтра “LPF work” в новом проекте:

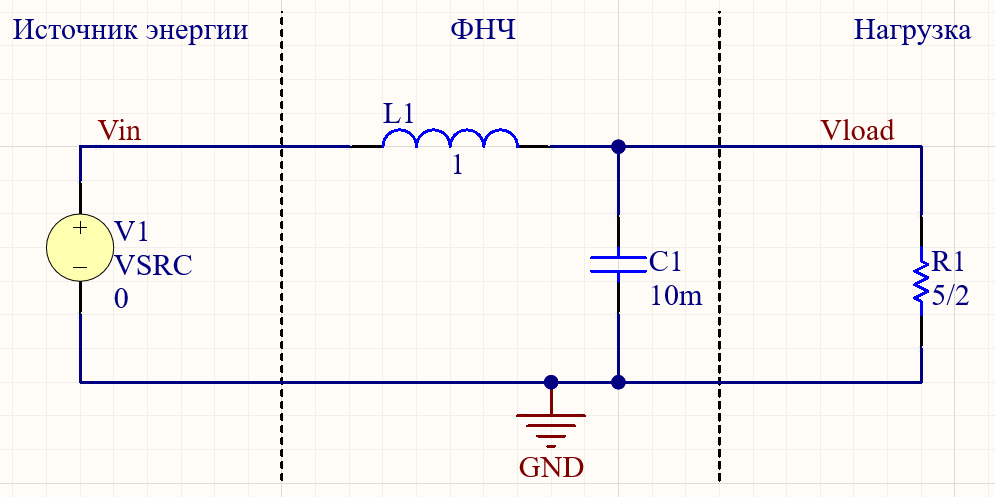
Для наглядности и удобства дальнейших рассуждений с помощью пунктирных линий схема условно разделена на 3 части. 

Задача ФНЧ - подавить все ненулевые гармоники спектра (переменные составляющие) Сигнала, при этом выделить ПС в нагрузку. Если LC цепь рассмотреть отдельно от Источника энергии, то учитывая, что внутреннее сопротивление идеального Источника энергии равно нулю, LC цепь будет представлять из себя параллельный колебательный контур, с резонансной частотой f0 равной:

f0 = 1/(2*ПИ*vL/C)

Очевидно, что для выделения ПС, резонансная частота f0 этого контура, должна находиться ниже частоты первой гармоники (по другому - основной гармоники) Сигнала ШИМ, при этом при подключенном источнике Энергии LC превратится в Г-образный ФНЧ, у которого частота среза его АЧХ будет равной f0 эквивалентного колебательного контура. 

Так же необходимо учитывать, на первый взгляд не явную характеристику, а именно совокупную добротность Q ФНЧ и Нагрузки в целом, т.к. при высокой добротности в нагрузке могут появляться паразитные выбросы на f0. 

В нашем случае добротность (Q) находится по следующей формуле:

Q = R1/(vL/C) , где ? = vL/C - характеристическое сопротивление контура, т.е.: Q = R1/?

Теория гласит, что в зависимости от добротности контура Q существует четыре режима его работы: колебательный, квазиколебательный, критический и апериодический:

• колебательный, квазиколебательный режими наблюдаются при Q>0,5, в этих режимах наблюдаются резонансные явления;

• критический режим при Q=0,5;

• апериодический режим при Q<0,5.

Для качественного и корректного подавления гармоник ШИМ сигнала, ФНЧ должен работать в докритическом режиме, т.е. когда не проявляются резонансные явления.

Давайте все сказанное изучим с помощью Симулятора, но так, чтобы значения L и C Симулятор  рассчитывал сам исходя из требований сопротивления нагрузки R1, частоты ШИМ сигнала f0 и совокупной добротности Q. 

После несложных рассуждений и преобразований получим:

1. Частоту среза ФНЧ ftr примем (предварительно) в 2 раза меньше f0: ftr = f0 / 2;

2. ? = R1/Q, а т.к. на частоте резонанса контура или среза ФНЧ ? = XL =XC, то:

   1. Lf = XL/ (2*ПИ*ftr) = ?/ (2*ПИ*ftr);

   2. Cf = 1/(XC * 2*ПИ*ftr) = 1/(? * 2*ПИ*ftr).

В нашей задаче появились новые переменные, которые на схеме никак не отображают значения ЭК, но напрямую (через формулы), на них влияют. Для их применения (новых переменных и формул на их основе), в Симуляторе есть прекрасный инструмент: Text Frame - это текстовая область из которой Симулятор берет информацию для дополнительного описания Схемы и моделирования в виде глобальных параметров (ГП) и зависимостей на их основе.

В нашем случае f0, Q, ftr, Ro, Lf, Cf и значение R1 - Rload будут являться ГП, при этом ftr, Ro, Lf и Cf являются так же результатом расчета формул в которые входят ГП: f0, Q, Rload. 

Для объявления глобальных переменных необходимо в любое удобное место схемы добавить область Text Frame, из Place » Text Frame главного меню или нажав Text Frame в раскрывающемся списке на панели инструментов. Далее в этой области необходимо прописать:

(Примечание: * Знак "+" в SPICE является признаком продолжения предыдущей строки. Перед знаком "+" не допускается использовать какие-либо другие символы, в том числе пробел.)

После создания и заполнения Text Frame, значения ГП Lf, Cf присвоим значениям L1, C1 соответственно нашей схемы, а в свойствах V1 присвоим AC Magnitude значение равное 1 (AC Magnitude - это параметр необходимый для запуска расчета AC Sweep):

и посмотрим АЧХ схемы ФНЧ на графике даже не зная конкретных их значений. Для этого нам необходимо настроить и применить следующий тип расчета AC Sweep.

Зная, что f0=10 Гц, хорошо бы посмотреть АЧХ ФНЧ в точке Vload минимум в 10-ти кратном масштабе от этой частоты в обе стороны, т.е. от 1 Гц до 100 Гц, при этом рассчитывая по 100 точек на декаду частоты (т.е. диапазон когда частота изменится в 10 раз):

Запускаем расчет (RUN)  AC Sweep и Смотрим график:

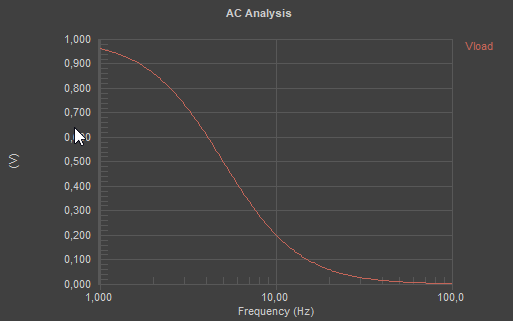
Обратите внимание: Частотная шкала у графика в логарифмическом масштабе. Давайте шкалу по амплитуде тоже выразим в логарифмическом масштабе, для этого необходимо в +Add Output Expression выбрать функцию представления - Magnitude (dB): 

Заметьте, что в Output Expression функция Vload  “обросла” новой функцией dB(Vload), которая логарифмирует представление нашего графика, нажимая еще раз на (RUN)  AC Sweep смотрим:

На графике мысленно видна асимптота правой наклонной его части, а что же находится левее, надо и там все видеть. Для этого достаточно немного перенастроить частоту старта AC Sweep с 1 Гц на 0,01 Гц (т.е. 10 миллиГц):

Зная исходные данные можно проверить себя на правильность наблюдаемых данных. Для этого на графике мысленно построим две пересекающиеся асимптоты (на рисунке ниже: две зеленые линии вдоль прямых участков графика), при этом точка пересечения будет на частоте 5 Гц, это и есть частота среза фильтра

 ftr = f0 / 2 = 10 / 2 = 5 Гц, что соответствует исходным данным задачи, а значит наши рассуждения и предварительные расчеты верны.

Глядя на этот график можно сделать еще один интересный вывод/проверку, любая цепь имеющая n реактивных компонентов (т.е. цепь n-го порядка) может дать максимальный (безрезонансный) наклон частотной характеристики:  n * 20 Дб/декаду, в нашем случае ФНЧ 2-го порядка у которой наклон правой части АЧХ, в соответствии с касательной графика, равен: (-10 Дб (при 10 Гц) - (-50 Дб (при 100 Гц))) = 40 Дб/декаду, что хорошо согласуется с предложенной формулой.

А что будет, если повысить добротность Q? Для этого достаточно в Text Frame отредактировать строчку +Q = 0.5, изменим Q в 10 раз: +Q = 5 и смело запускаем расчет:

Сравним график с предыдущим:

1. Цель ФНЧ это подавить все гармоники начиная с основной (f=10 Гц), при Q=0,5 основная гармоника была ослаблена примерно на 14 Дб, тогда как при Q=5 ослабление уменьшилось до 10Дб, т.е. характеристики ФНЧ ухудшились.

2. На частоте среза ftr = 5Гц появился крайне нежелательный ярко выраженный резонанс, т.к. он может внести в схему неожиданную Обратную Связь (ОС), которая может в корне изменить режимы работы всей схемы в целом.

3. Наклон правой, зарезонансной части АЧХ остался прежним -40 Дб/декаду.

Мы увидели как влияет Добротность системы ФНЧ+Нагрузка в критическом и колебательных режимах на характеристики ФНЧ, на основе чего сформулируем главный вывод применения ФНЧ в нашем случае: При проектировании ФНЧ для выделения ПС из Сигнала ШИМ необходимо, чтобы частота среза ФНЧ, была ниже основной гармоники Сигнала и исключены псевдоколебательный и уж тем более колебательный режимы работы ФНЧ. 

Теперь пришло время посмотреть, как это все работает ВМЕСТЕ, в виде швейного цеха, где ткань энергии нарезается ножницами - ключами и тут же сшивается швейной машиной - ФНЧ в третьей части нашего рассказа: “Фабрика пошива качественной энергии”.