С развитием информационных технологий профессия DS стала чрезвычайно популярна. Сейчас почти каждый может имея ПК и установленный на нем стандартный пакет Python, анализировать данные и строить на их основе прогнозы.

Во многих случаях достаточно просто скачать библиотеку для анализа данных, и получить неплохие результаты. При этом процессы, происходящие внутри используемых пользователем библиотек, остаются за пределами понимания, что зачастую влечет за собой неспособности поверхностного пользователя правильно интерпретировать полученные данные, особенно если это нейросеть.

В статье представлен пример реализации спектрального анализа функции на примере реальных данных. Этот математический метод позволяет провести более глубокий анализ изменения функции переменной во времени, найти периодические составляющие. Его применение способно существенно повлиять на результат предсказания целевой переменной, поскольку позволяет учитывать сезонные и другие периодические колебания.

Предположим, перед аналитиком стоит задача исследовать информацию о количестве людей на сайте в определенное время в определенный день, имея выборку по посещению сайта за несколько месяцев каждые 30 минут. И сделать прогноз посещения на будущий период.

Данные по посещениям представлены на графике ниже

Как видно из графика, характер данных имеет явную периодическую составляющую. Разложим наши данные в ряд Фурье по следующей формуле.

Ниже представлена функция, которая принимает в качестве аргумента датафрейм с исходными данными. Эта функция использует только самые простые библиотеки, чтобы мы могли использовать декоратор компиляции. Расчет при большом объёме данных может занять значительное время, а компилятор ускоряет скорость расчета в 100 раз.

@numba.jit (nopython = True)
def period(df['SA']):
    a , b = [] , []
    a.append(dfv.mean())
    b.append(0)
    for i in range(1 , len(dfv)//2 + 1):
        p = 0
        q = 0
       for j in range(1, len(dfv)+1):
p = p + dfv[j - 1] * math.cos(2 * math.pi * i * j / len(dfv))
q = q + dfv[j - 1] * math.sin(2 * math.pi * i * j / len(dfv))
       a.append(2 / len(dfv) * p)
       b.append(2 / len(dfv) * q)
    gramma = []
    for i in range(len(a)):
k = (a[i] ** 2 + b[i] ** 2) * len(dfv) / 2
gramma.append( k )
    return a, b, gramma

Результатом работы этой функции являются три списка, два с коэффициентами a и b из формулы выше для разложения в ряд Фурье и один с квадратами амплитуды для построения графика периодограммы.

Ниже на графике представлены две кривые, одна - реальные данные, другая - это прогноз, использующий разложения данных в ряд Фурье с учетом всех гармонических составляющих (N/2), где N - число наблюдений. Как мы можем видеть, прогноз полностью совпадает с реальными данными.

Для определения наиболее значащих гармоник необходимо построить периодограмму. По оси х - это порядковый номер гармоники от 0 до Т/2, по оси Y - значение квадратов амплитуды, полученных из функции выше.

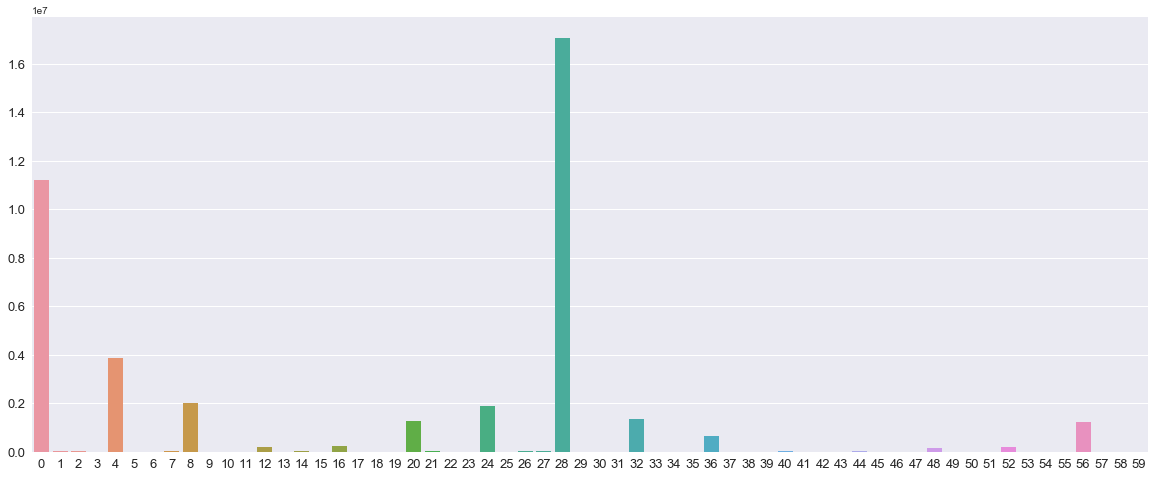
Полученный график периодограммы показывает какие гармоники являются наиболее значимыми, то есть оказывают наибольшее влияние на значение функции.

Для прогнозирования и анализа данных нам нужны только гармоники с высокой амплитудой, иначе нельзя будет использовать для прогнозирования, так как это приведёт к переобучению модели – точному соответствию тренировочной выборке и слабому результату на тестовой.

Реализовать выбор гармоник с самой высокой амплитудой можно следующим образом:

zn = [0,4,8,20,24,28]
for i in range(len(a)):
if i not in zn:
a[i] , b[i] = 0,0
prog = []
for i in range(1 , len(df) + 1):
    r = 0
    for j in range(len(a)):
        r = r + a[j] * cos(2 * pi * j * i/len(df)) + b[j] * sin(2 * pi * j * i/len(df))
prog.append(r)

y1 = df['SA']
y2 = prog
fig , ax = plt.subplots()
plt.plot(x, y1 , c = 'hotpink' , linewidth = 4 ,label ='Данные')
plt.plot(x, y2, c = 'Black', linewidth = 3,label ='Прогноз')
ax.legend(loc = 'upper center' , fontsize = 25 , ncol = 2 )
fig.set_figwidth(20)
fig.set_figheight(6)
fig.suptitle("Посещение сайта")
plt.show()

Как видно из графика выше, применение описанного метода позволяет получить очень хороший прогноз с использованием всего шести наиболее значимых гармоник. В нашем примере это 0,4% от всех 1344 гармоник.

Таким образом, результатом применения описанного метода является новая независимая переменная, позволяющая существенно улучшить прогноз.

Конечно, не все исходные данные будут иметь такую явную периодическую составляющую как в этом примере, но тем и хорош спектральный анализ, что он позволяет выявлять даже неочевидные или скрытые периодические закономерности.