Хабр, привет! 

Под катом хотелось бы поговорить об опыте участия нашей команды из лаборатории моделирования природных систем Национального центра когнитивных разработок Университета ИТМО в хакатоне Emergency DataHack 2021. И победы в нём :)

Что за хакатон?

Emergency DataHack - это хакатон, который проводится совместно с МЧС России, где несколько десятков команд в течение двух дней анализируют данные и строят модели для предотвращения чрезвычайных ситуаций. 

Хакатон проходил с 28 по 30 мая 2021 года. Заинтересовавшимся хакатоном предлагаем проследовать по ссылке (возможно, вы захотите попробовать свои силы в нём же, но в будущем году).

Зачем хакатон? 

Во первых, стоит участвовать, потому что это хорошая возможность весело провести время и при этом получить новые знания и опыт. 

Во вторых, можете опробовать свои разработки на “боевой” задаче. Подобный интерес был и у нас: в рамках хакатона использовался разрабатываемый в нашей лаборатории моделирования природных систем open-source AutoML фреймворк FEDOT (https://github.com/nccr-itmo/FEDOT). Это дало возможность обнаружить его сильные и слабые стороны. 

Если вы не знаете, что такое AutoML, то можете посмотреть на данную картинку (этого почти достаточно, чтобы разобраться):

Если хочется разобраться чуть подробнее, то можете обратиться к нашим статьям на хабре (Как AutoML помогает создавать модели композитного ИИ — говорим о структурном обучении и фреймворке FEDOT) и TowardsDataScience (AutoML for time series: advanced approaches with FEDOT framework).

Немаловажным фактором выбора именно этого хакатона была его тематика: помимо разработки академического AutoML-фреймворка, мы пишем научные статьи и выполняем различные проекты, связанные с моделированием чего-либо, где это что-то периодически повреждается и разрушается под воздействием природных процессов. Как правило это моделирование связано с гео- науками: метеорологией, гидрологией, океанологией, геологией и др. Мы решили попробовать совместить наш опыт разработки алгоритмов для решения географических задач и AutoML в рамках данного хакатона. Для этого мы собрались с коллегами под знаменем “NSS_lab team”.

Зачем пост?

Немного слов про мотивацию для написания данного поста. Вышло несколько новостей, где было написано, что мы сделали, без технических деталей, зато с преукрашиванием в духе “Российские ученые повернули реки вспять” (отсюда и название поста). 

Подборка забавных новостей о победе: 

• Искусственный интеллект поможет предотвращать наводнения во время половодий

• Паводки и половодья теперь под контролем российских ученых

• Российские ученые придумали, как предотвращать наводнения

Спойлер: не верьте всему, что пишут в новостях, лучше читайте хабр - тут мы пишем как всё было на самом деле. Собственно, вот мы и решили прояснить ситуацию. С другой стороны, описанный ниже подход может пригодиться при решении похожих задач как в рамках хакатона, так и просто при работе с сильно разливающимися в период половодья реками. 

Описание задачи 

В хакатоне было несколько треков, - наш был второй. Задание звучало так: “Построить предиктивную модель, которая позволит в весенний период оценивать суточное приращение максимального уровня воды на 7 дней вперед на определенных участках реки Лена”. 

Немного про актуальность

На реке Лена иногда случаются разрушительные наводнения, которые приносят серьезный вред жителям Республики Саха (Якутия). Особенно опасны такие наводнения в период половодья (одна из фаз водного режима реки, ежегодно повторяющаяся в один и тот же сезон года, — относительно длительное и значительное увеличение водности реки, вызывающее подъём её уровня (ист. википедия)). Почему разливы особенно опасны именно в весенний период? Во многом из-за ледовых заторов (нагромождений льдин), которые образуются на реке и играют роль своеобразных плотин, что приводит к резкому поднятию уровня воды выше по реке. С другой стороны, таяние снега на водосборном бассейне тоже играет роль - стаявший снег так или иначе со временем попадает в русло реки. Всё это приводит к повышению уровня.

Для большей наглядности, можно изучить гидрограф стока для одного из гидрологических постов:

Черными линиями показаны реализации расхода воды на данном гидропосте в различные годы с 1985 по 2019 годы. Синей линией показано среднее значение. Как видно из графика, весной имеется взрывной рост у данного показателя, это и есть пресловутое половодье.

Система предсказания уровня воды в реке позволила бы эффективно распределять ресурсы для предотвращения наводнений, или для своевременной эвакуации населения.

Гидрологических постов, для которых требуется давать прогноз было 10 штук. Для решения предоставлялись разнородные данные: 

• Уровни воды на гидропостах в виде временных рядов с суточной дискретностью;

• Метеопараметры, фиксируемые на гидрологических постах, а также дополнительная информация о событиях на реке;

• Данные о метеоусловиях с метеостанций. Тут есть почти всё: от температуры воздуха и осадков, до высоты снежного покрова, однако данные относятся к точкам, расположенным на некоторых расстояниях от гидрологических постов.

Данные имеют пропуски, некоторые параметры требуют интерполяции в соседние точки. Также метеопараметры фиксируются в разные моменты времени: есть срочные наблюдения, среднесуточные и среднемесячные значения параметров. Какие-то показатели фиксировались только в сроки, другие - только как среднесуточные значения и так далее.

Решение. Основные идеи

Итак, необходимо решать задачу регрессии / прогнозирования временного ряда, где целевая переменная - показатель того, насколько вырос уровень воды за сутки. 

Сначала разберёмся с целевой переменной: “суточное приращение максимального уровня воды” звучит слишком сложно (по крайней мере, для нас). Давайте упростим - будем прогнозировать не приращение, а просто максимальное суточное значение уровня воды. Перерасчет в приращение осуществим уже в последний момент, благо сделать это не так сложно. 

Значение уровня воды на гидрологических постах изначально можно предсказывать просто “в лоб”, используя прогнозирование одномерных временных рядов. Хорошо, что инструмент под рукой - FEDOT довольно неплохо справляется с задачей прогнозирования временного ряда.

Пока AutoML строит предсказания на временных рядах, можно потратить время на творческую работу - разработку более продвинутых моделей и подготовку данных для этих “сложных” моделей. 

Решено было использовать многоступенчатый подход: требуется построить ансамблевую модель из нескольких составных частей. Первая часть - модель прогнозирования временного ряда. Почему именно она? - потому что мы ее уже построили, и она в данный момент уже даёт первый прогноз. Подробности её реализации будут ниже, пока назовём эту модель “Модель 1”. 

“Модель 2”- эта модель должна учитывать метеоусловия, а также события, которые происходят на реке выше или ниже по течению. Построить её можно на основе многомерной регрессии (это регрессия, когда прогноз даётся не на один элемент, а на несколько, в данном случае, на семь элементов).

“Модель 3”, - интерпретируемая модель. Такая, которая позволила бы пользователю, или лицу, принимающему решения, убедиться в корректности прогноза. Мы решили, что проверенные временем классические подходы к моделированию могут хорошо подойти на эту роль. 

Предобработка данных

Первый этап предобработки - интерполяция значений в нужные узлы. 

Как было сказано выше, не все параметры относятся к тем же географическим точкам, где у нас расположены гидрологические посты. Проблему можно проиллюстрировать следующей картинкой (рисунок 1). 

Из рисунка видно, что значения метеопараметров в определенный момент времени хоть и известны, но не в тех точках, в которых нам это надо. Первое, что приходит в голову - применить какой-нибудь простой алгоритм интерполяции. Как говорится, лишь бы работало. Но при этом хотелось бы сохранить гибкость подхода: некоторые метеостанции, хоть и расположены близко (по координатам долготы и широты) к интересующему нас гидропосту, могут быть с ним связаны очень слабо. Это может происходить из-за неоднородностей рельефа. Например, точки находятся близко друг к другу, но ближайшая метеостанция, как и гидрологический пост, расположена в низине, а две соседние - в котловинах среди хребтов. Тогда лучшим решением будет брать значения только с ближайшей метеостанции и не производить интерполяцию вовсе. А в другом случае хорошим решением будет усреднить значения по пяти соседним метеостанциям. Билинейная интерполяция или интерполяция методом ближайшего соседа таким требованиям не отвечает.

Поэтому решено было реализовать подход, где интерполяцией значений будет заниматься модель машинного обучения K-ближайших соседей (K-nn). Принцип работы алгоритма можно увидеть на анимации ниже:

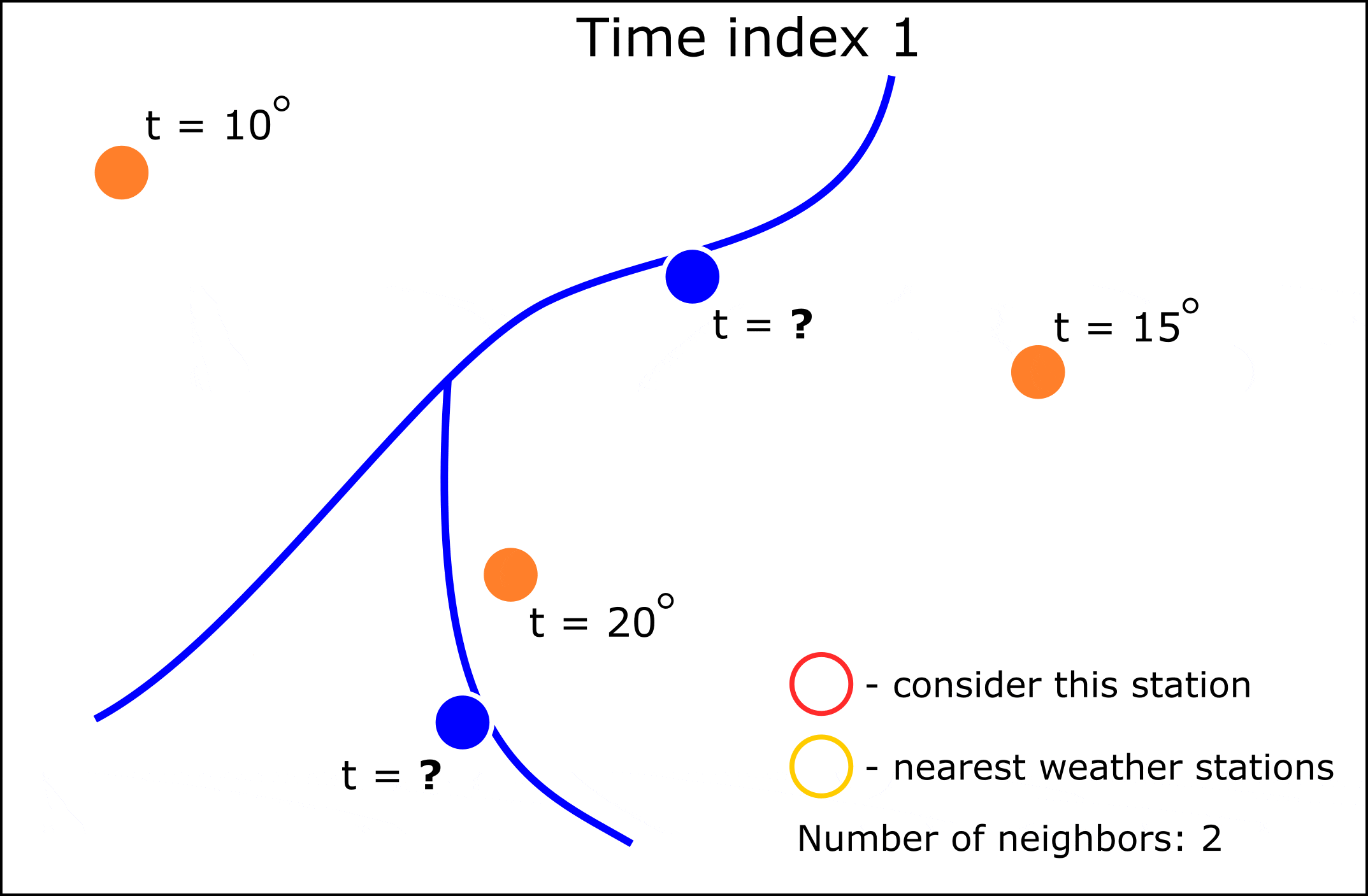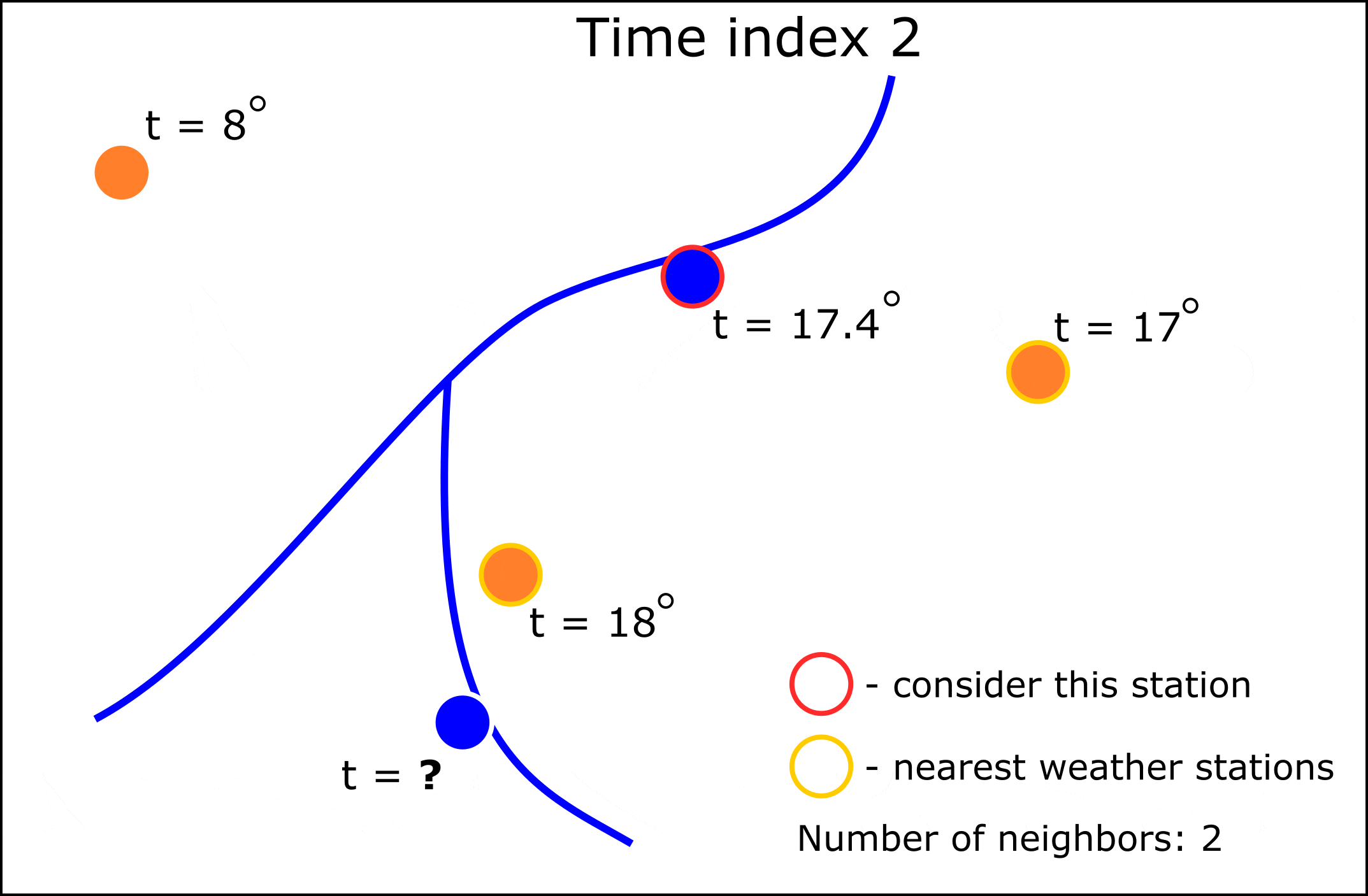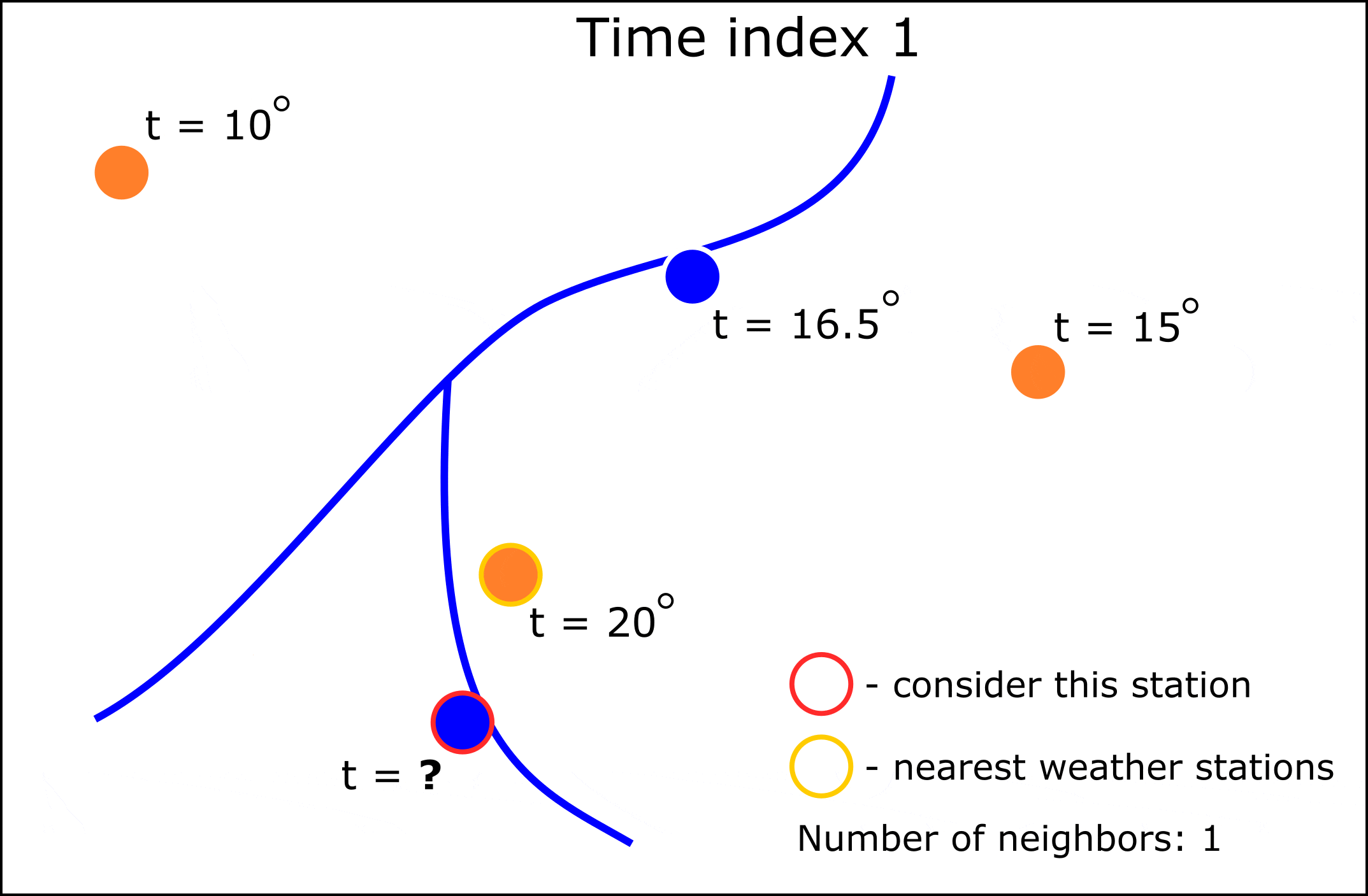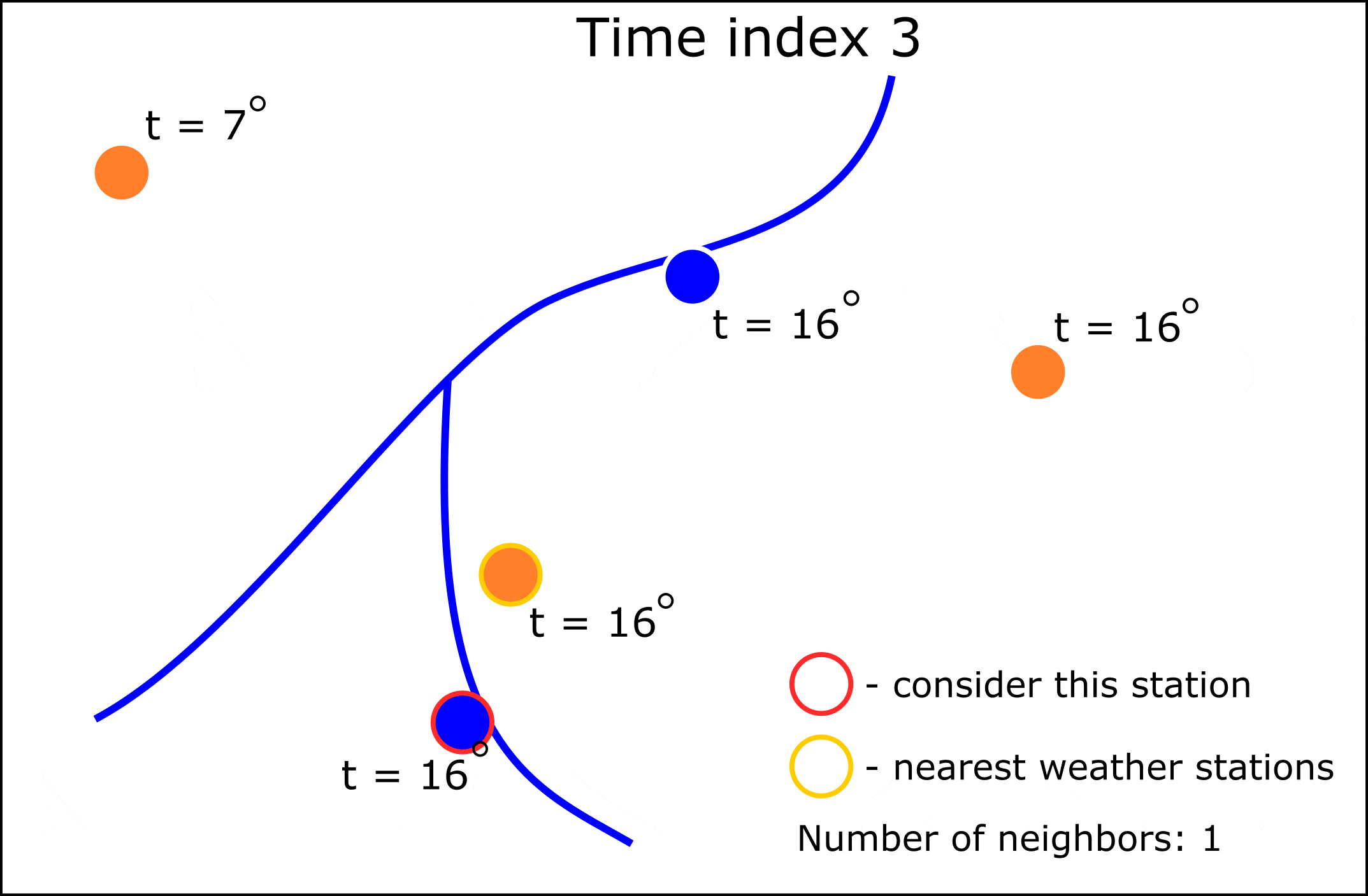
Как видно из анимации, мы можем для требуемых гидрологических постов изменять количество соседних метеостанций. Предсказание нового значения метеопараметра в данном случае происходит на основе двух предикторов: широты и долготы. При этом “интерполироваться” при таком подходе могут и категориальные показатели, для этого потребуется заменить регресионную K-nn на модель K-nn классфикации. 

Небольшой дисклеймер. Мы понимаем, что описанный выше подход не является оптимальным для интерполяции метеопараметров. Если бы всё было так просто, то не нужны бы тогда были метеорологические модели, сетки реанализа с усвоенными данными дистанционного зондирования и сложные алгоритмы расчета метеорологических характеристик. Но для решения задачи в рамках двухдневного хакатона мы приняли этот подход как наиболее подходящий. 

Второй этап - заполнение пропусков. 

Данные наблюдений зачастую предоставляются с большим количеством пропусков. Они могут быть различной длительности (в нашем наборе данных достигали целого года!), и наблюдаться как только для отдельных переменных в наборе данных, так и для всех наблюдаемых показателей. Так как терять целый дополнительный параметр очень не хочется даже при наличии больших пропусков, было принято решение заполнить их, основываясь на имеющихся предшествующей и последующей частях временного ряда.

Сразу отметим, что естественные пропуски в данных по типу показателей, связанных с ледовой обстановкой и снежным покровом в теплое время года нами не заполнялись. 

Главным помощником в заполнении пропусков незначительной длины (менее полугода) снова стал FEDOT. Основная функциональность фреймворка в области заполнения пропусков опирается на прогнозирование временных рядов. Для каждого пропуска осуществляется прогнозирование значений в “интервал с пропуском” на основе предыстории (часть ряда слева от пропуска) и последующего после пропуска поведения величины (часть ряда, расположенная справа от пропуска). Сначала прогнозная модель даёт предсказания на предыстории, затем на инвертированной последующей части ряда. После этого прогнозы соединяются при помощи взвешенного среднего. 

Стоит обратить внимание на местоположение пропуска: важно, чтобы начало временного ряда (или конец при инвертировании временного ряда) располагал достаточным количеством значений для начала прогнозирования. При таком неудачном пропуске можно воспользоваться некоторыми допущениями и заполнить необходимое количество значений простыми статистическими методами (средними, медианными значениями и т.п.).

Для заполнения длительных пропусков (длиной более полугода) был использован более сложный подход. Так как ход большинства метео- и гидрологических данных определяется сезонами, заполнять длительные пропуски только лишь прогнозированием - неудачная затея, так как пиковые значения (которые и были пропущены) очевидно теряются. В таких случаях мы использовали следующий подход. Так как набор данных представляет собой многолетние наблюдения представляется возможность декомпозировать временной ряд и извлечь нужную нам сезонность и тренд, что даже с учетом пропусков является решаемой без особых потерь задачей. 

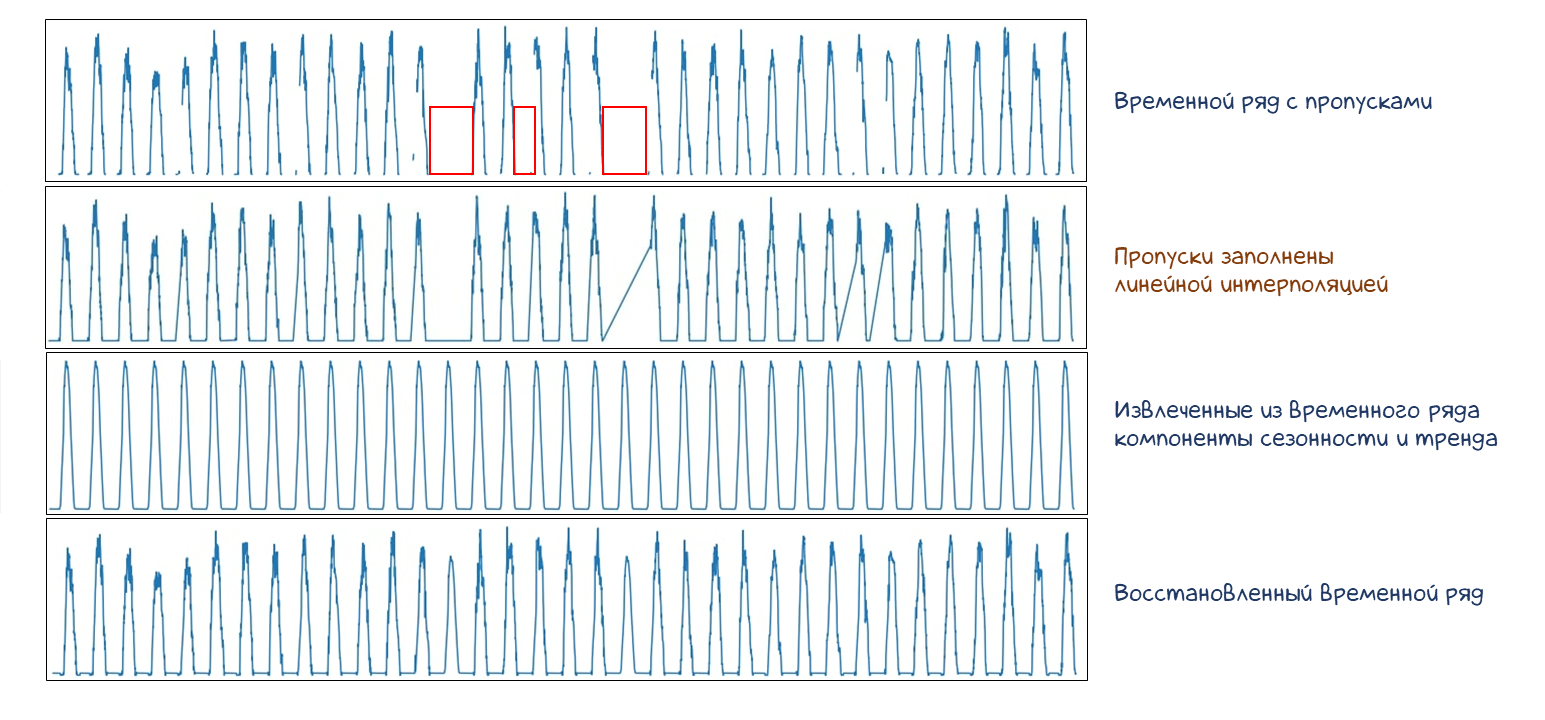
Для декомпозирования временного ряда использовалась библиотека statsmodels. Таким образом компонента сезонности из “разложенного“ временного ряда позволяет (пусть и в глобальном масштабе) восстановить пиковые значения временного ряда. Однако использование только сезонной составляющей для заполнения пропуска не отражает абсолютных значений, а скорее представляет собой амплитуду колебаний. Таким образом, для корректного заполнения пропуска к сезонной составляющей добавлялось медианное значение трендовой составляющей, что позволило соотнести полученные значения с основным временным рядом. Такой подход был особенно действенным для заполнения пропусков в расходах воды и температурах, так как колебания этих показателей ярко выражены, а пропуски в них довольно значительны, особенно с учетом что эти параметры являются основными предикторами для наших моделей.

Дополнительные источники данных

Которые нам не пригодились…

Итак, мы начали смотреть в сторону открытых источников данных. Первое, что потенциально может быть полезно практически при любой работе с географическими данными - это матрица высот для требуемой территории. Мы решили взять глобальную цифровую модель рельефа (ЦМР) - SRTM. На основе этой ЦМР мы построили профили для гидрологических постов (рисунок 3).

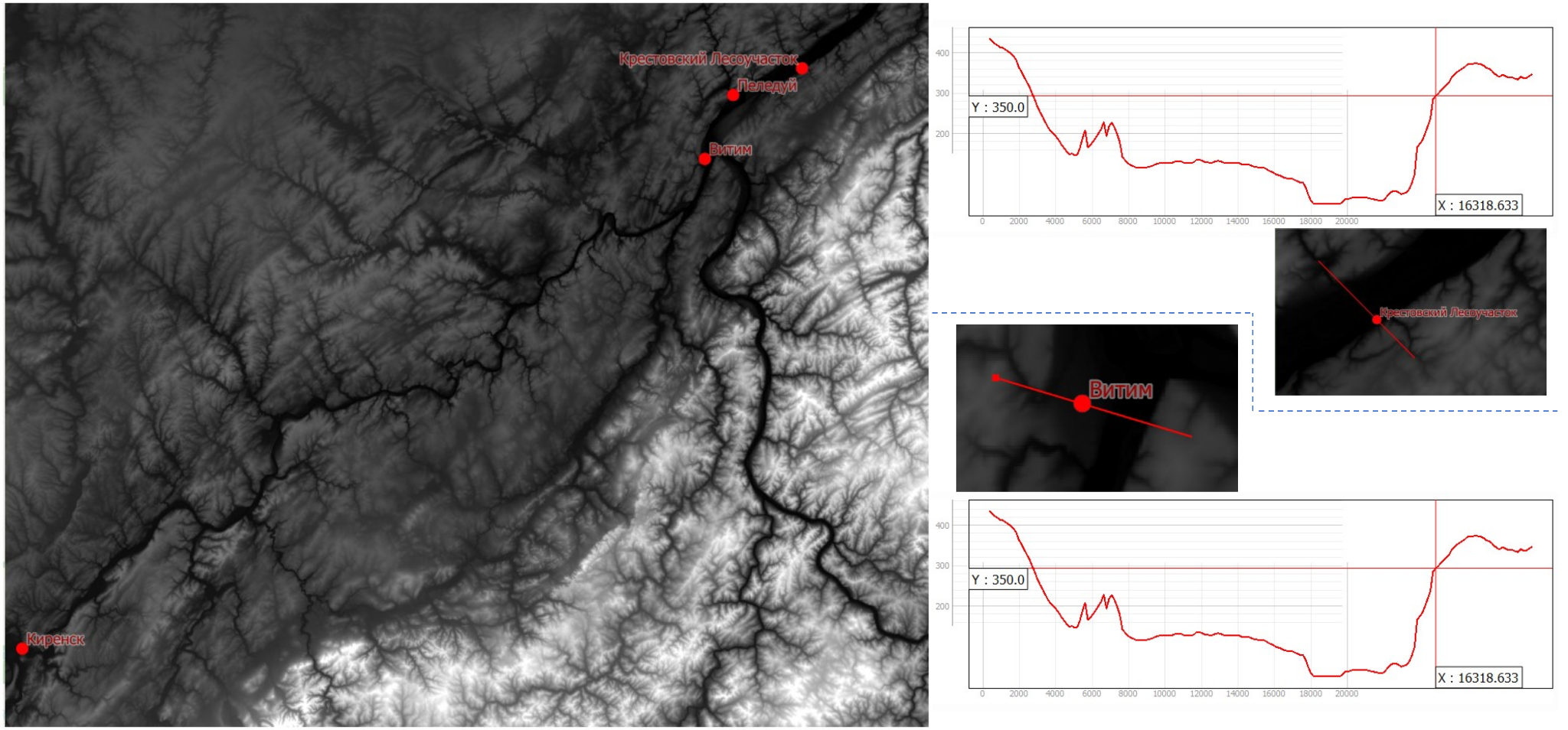
Мы подумали о том, что эти данные можно использовать для расчета уровней, если нам будут известны скорость течения и расход. Мы об этом подумали ещё до того, как нам предоставили доступ к данным... Но скорость течения нам не предоставили. В итоге, всё, что мы смогли сделать с данными - это примерно разобраться в особенностях рельефа створов реки на гидрологических постах. 

Теоретически, мы могли использовать рельеф и в наших моделях в дальнейшем, но времени не хватило.

Модель 1. Прогнозирование временного ряда

Мы уже писали статью на хабр на тему прогнозирования временных рядов с помощью AutoML. Там изложены основные принципы построения пайплайнов для прогнозирования последовательностей, которые использует FEDOT. 

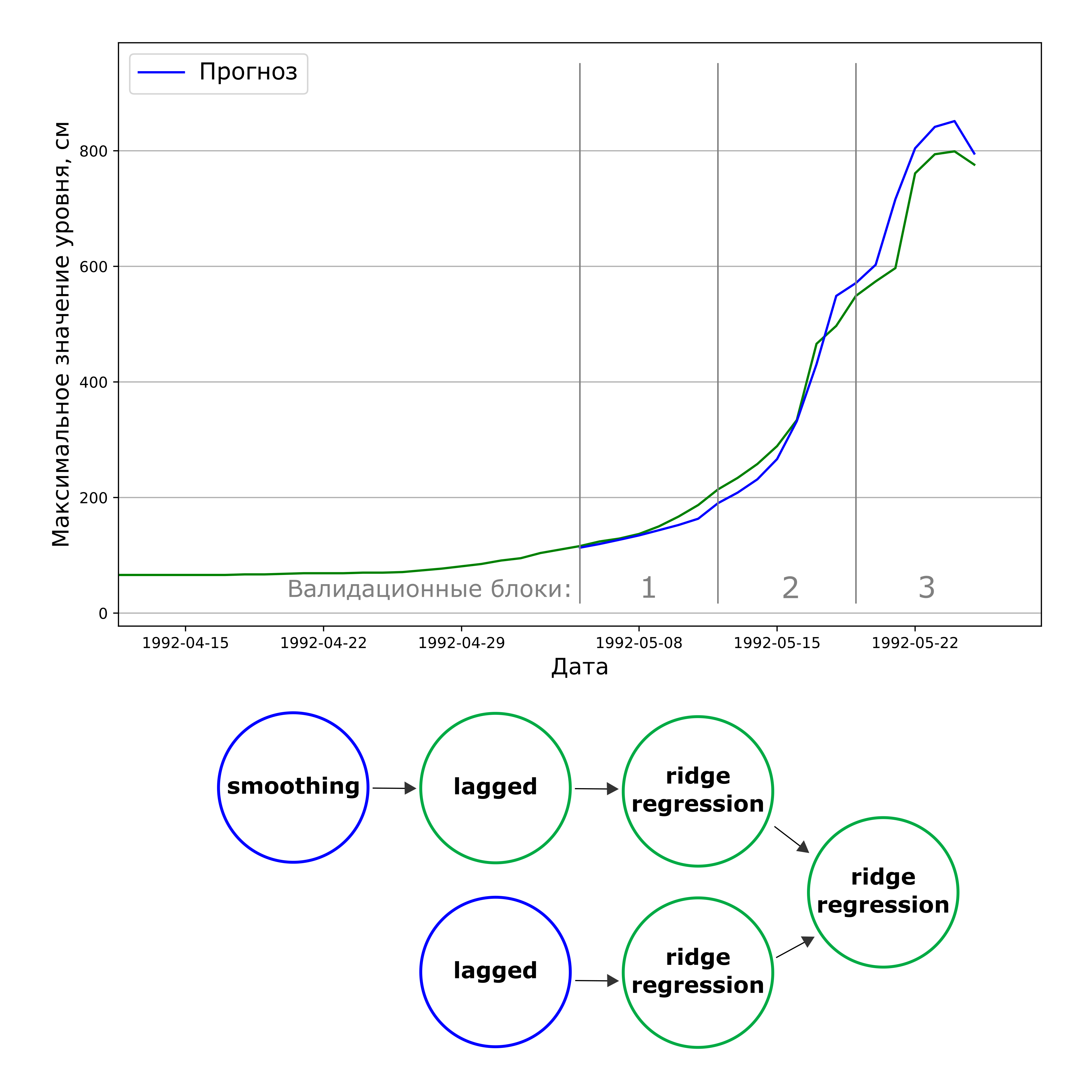
Тем не менее, кратко изложим то, как именно строится модель прогнозирования временного ряда. Начинается всё с преобразования одномерного временного ряда в таблицу лагов (траекторную матрицу). Так, признаками в таблице являются текущее  и предыдущие значения временного ряда в моменты времени t, t-1, t-2 и т.д. Целевыми переменными в таком случае становятся значения в моменты времени t+1, t+2, t+3 и т.д. После этого преобразования на таблице может быть обучена подходящая модель машинного обучения. Можно, пользуясь технологией стекинга, объединять несколько моделей в единый пайплайн. Этим и занимается FEDOT. 

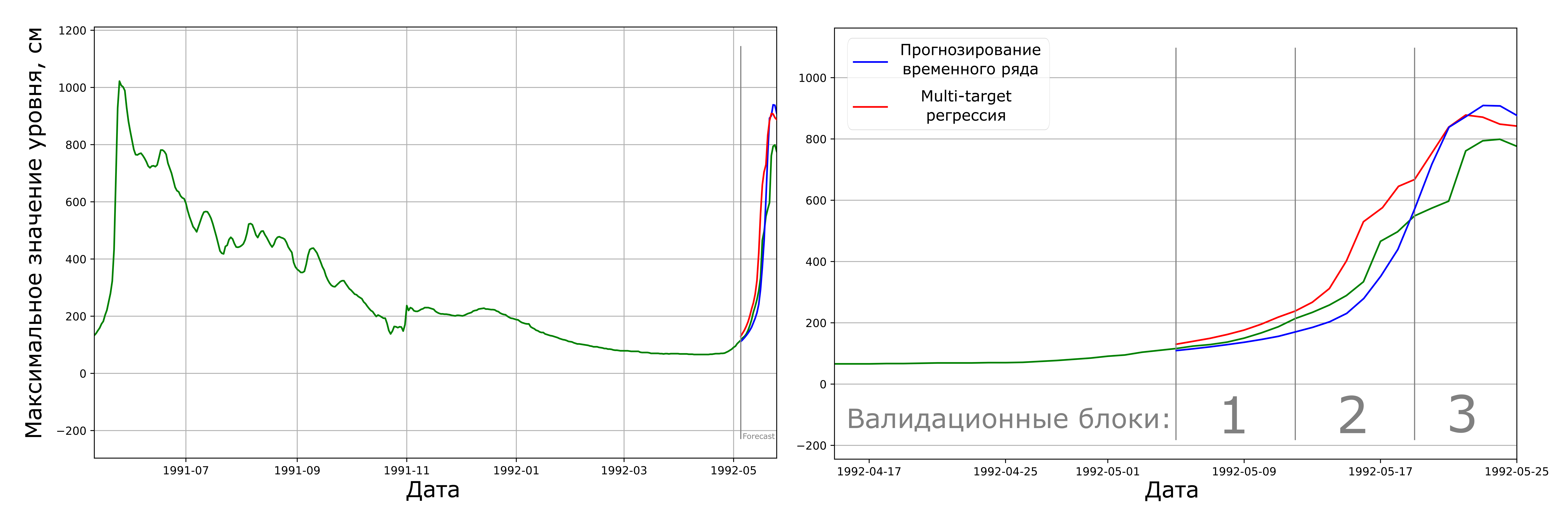
Если посмотреть на пример получившихся прогнозов на трёх блоках валидации, можно увидеть, что модель показывает себя очень достойно (рисунок 4).

Модель 2. Многомерная регрессия

Эта модель отвечает за учет метеопараметров и данных о событиях, происходящих на реке. Начнём с концепции: планируется решать multi-target регрессию следующего вида (рисунок 5)

 Целевых переменных в таблице всегда семь, с 21 по 27 апреля в данном примере, что равно горизонту прогнозирования. При этом признаки могут агрегироваться за разные временные промежутки. Так например, сумму осадков можно считать как за 10 суток, предшествующих рассматриваемому дню, так и за 20, и за 30.  

Как понятно из описания признаков, они являются производными от исходных метеопараметров. Агрегировать параметры можно по разному: брать сумму, среднее значение, амплитуду, наиболее часто встречающееся значение и так далее.

Интересно будет поближе рассмотреть пример с амплитудой высоты снежного покрова. Сразу оговоримся, что в случае с высотой снега это не совсем амплитуда, когда значение рассчитывается по формуле max - min. Для высоты снега мы используем разность между первым и последним значением за выбранный промежуток: first - last. Рассмотрим пример, когда мы агрегируем показатель для 20 апреля 2020 года и берём промежуток времени для агрегирования, например, 10 суток: в таком случае мы будем вычитать из значения высоты снега, зафиксированного 10 апреля, то значение, которое было получено 20 апреля, и так узнаем “сколько мм снега стаяло за выбранный промежуток времени”, также поступим для пары 11.04 и 21.04 и так далее. Естественно, можно считать и просто амплитуду, но мы поступили вот таким образом. Сделано это было для того, чтобы разделить периоды, когда снег выпадает, и следовательно, высота снежного покрова растет, и когда снег интенсивно тает. В случае с амплитудой это сделать не получилось бы, хотя мы и считали амплитуду в первых версиях этого подхода.   

Чтобы лучше разобраться с этим, давайте посмотрим на график, где показаны одновременно максимальный за сутки уровень воды и “амплитуда” снежного покрова (рисунок 6). 

Интерпретировать пики оранжевой кривой можно как “периоды наиболее интенсивного снеготаяния”. В таком случае экстремумы ниже нуля для оранжевой же линии можно назвать “периодами интенсивного снегонакопления”. Нас, конечно же, интересуют именно первые. 

Так, из графика видно, что во время выхода “амплитуды” снега на пик, начинается рост уровней и продолжается ровно до того момента, пока “амплитуда” не достигнет значений, близких к нулю  - тогда же наблюдаются самые высокие максимальные уровни. 

Похожие преобразования мы сделали и для других метеопараметров. Однако есть один важный предиктор, который стоит рассмотреть поближе (даже на рисунке 4 он специально поэтому подсвечен красным) - сумма рангов важности событий. События здесь - это то, что происходит на реке. Они фиксируются в виде фраз “Навалы льда”, “Волнение”, “Неполный ледостав”, “Затор выше поста” и т.д. Напрямую фразы в модель не передать, да и процедуру агрегации таким фразам тоже пройти надо, чтобы можно использовать в модели многомерной регрессии, но пока непонятно каким образом. 

Мы поступили так - сопоставили событиям ранги. Ранги, это наша экспертная оценка того, насколько большое влияние событие оказывает на поднятие уровня воды в половодье. Ранги изменяются от 0 до 3, где 0 - неважное событие, а 3 - очень важное. В итоге была сформирована таблица, фрагмент которой представлен ниже.

Таблица 1. Некоторые события и ранги важности для них

Теперь вместо словесных описаний мы получили порядковую величину. Таким образом сейчас мы можем сказать, что “Затор ниже поста” (3) больше, чем “Река пересохла” (0). Далее данные необходимо сагрегировать, как мы делали раньше с метеопараметрами. Для рангов было решено посчитать сумму за определенный период. Если сумма рангов большая, то, вероятно, стоит ожидать заметного изменения уровня воды в реке, и наоборот. 

Итак, признаки сформированы, пришло время определяться с моделью, которая будет отображать признаки в отклики… Но мы этого делать не будем. AutoML сам построит подходящую модель, сам определит методы предобработки и трансформации данных, поэтому просто запустим FEDOT и перейдем к следующему шагу.

Примеры структур полученных пайплайнов можно увидеть на рисунке 7. 

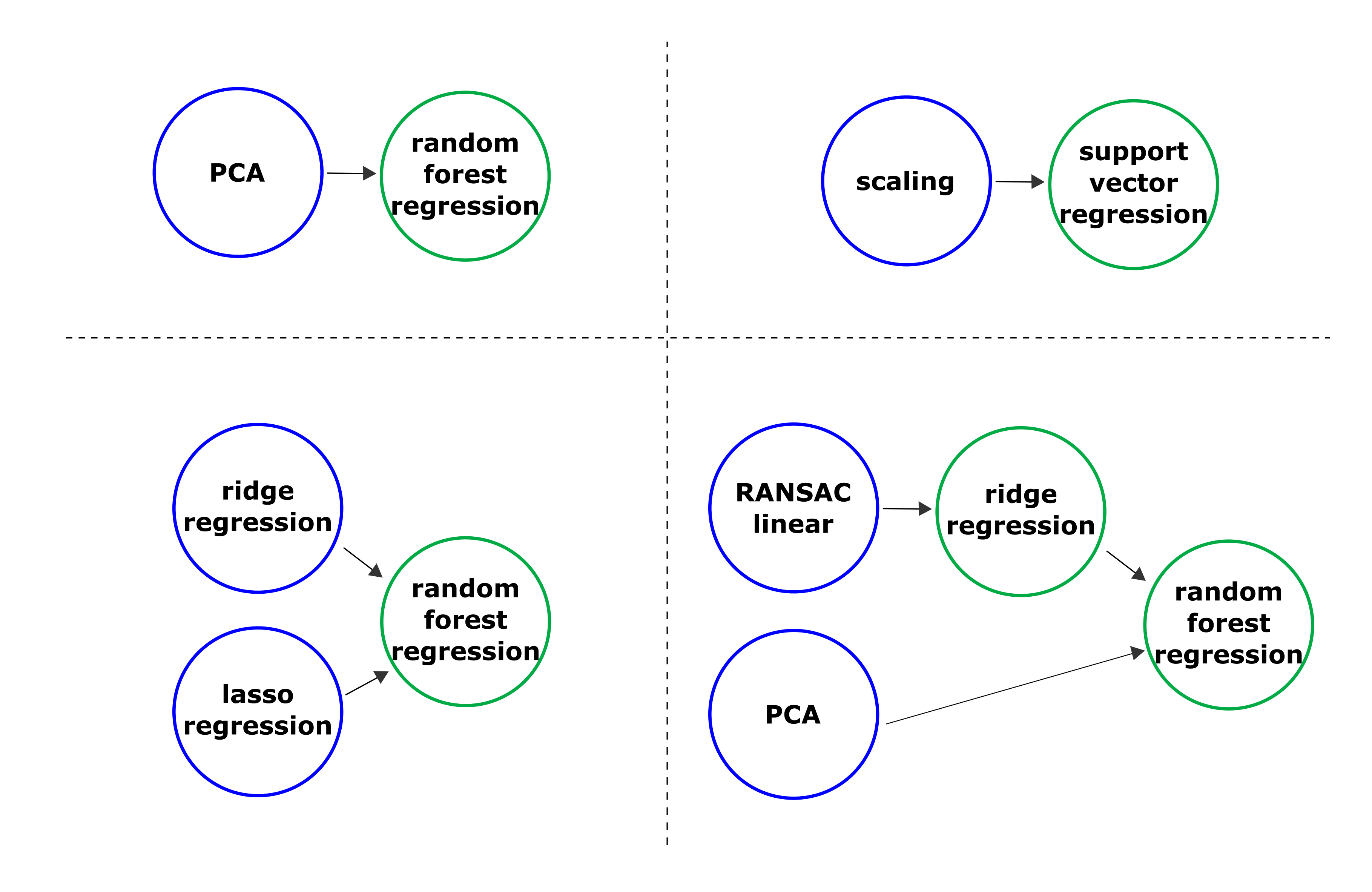
Результаты прогноза модели, состоящей уже из двух частей, можно увидеть на рисунке ниже (рисунок 8). 

Модель 3. Физическая модель

Для одного из гидрологических постов решено было построить физическую модель. Для этого воспользовались существующими подходами к физическому моделированию (а именно Snowmelt Runoff Model) и реализовали алгоритм на чистом Python’е. После интегрировали подготовленную модель в наш общий пайплайн. Получилось такое гибридное моделирование: что-то мы прогнозируем при помощи машинного обучения, что-то - при помощи физической модели. 

Вы можете спросить зачем мы всё делали именно так, зачем физ. модель писать за одну ночь, зачем на Python? - Не спрашивайте, мы просто флексили. В конце концов, хакатон нужен в том числе и для этого. 

Итак, как это работает. За основу нашего подхода мы взяли относительно старую и простую модель SRM (Snowmelt-Runoff model), так как её легко воплотить в коде и провести тюнинг, а нам было интересно попробовать применить комбинированный подход, использующий и детерминистическую модель, и методы машинного обучения, вне зависимости от сложности подходов. Далее под тюнингом модели мы будет подразумевать определение её гиперпараметров, например, используемых для расчетов коэффициентов и иных величин, которые принимаются за постоянные при вычислениях. Необходимость подобного тюнинга связана с тем, что мы не можем напрямую узнать интересующие нас параметры модели, и нам приходится делать некоторые предположения о них на основе наблюдаемых явлений.

Используемая модель создана для воспроизведения суточного стока с небольших горных водосборных бассейнов, при вычислении которого необходимо оценивать как вклад снеготаяния, так и дождевой воды. При этом модель может быть адаптирована и для использования и в иных условиях и с иными данными: в нашем случае, при расчёте расхода воды в створе мы имели различные метеорологические и снегомерные данные, интерполированные к створу, а также измерения уровня воды в створе выше по течению. При отсутствии лучших альтернатив, вместо полноценного интегрирования слоя осадков по водосборному бассейну, привязанного к нашему моделируемому створу, мы были вынуждены использовать значения в точке створа. Таким образом мы получаем следующее соотношение для расхода в момент времени n:

• - расход воды на n+1-ом шаге по времени в m-ом створе реки;

• - коэффициенты стока, отражающие долю попавших в реку осадков по отношению к выпавшим для твёрдых и жидких осадков соответственно;

• - коэффициент градусо-дней, отражающий изменение глубины снега в соответствии с одним градусо-днём;

• - доля поверхности, покрытой снегом;

• - значение температуры, скорректированное под среднюю высоту в водосборе;

• - слой жидких осадков, для твёрдых осадков предполагается, что они учитываются в доле покрытой снегом поверхности;

• - коэффициент рецессии стока, отображающий снижение расхода в дни с нулевым влиянием осадков и снеготаяния;

• - коэффициент, отвечающий за перенос воды от следующего вверх по течению гидрологического поста с измерениями расхода воды.

• - площадь водосбора, сток с которого учитывается для обрабатываемого створа, но не для следующего вверх по течению гидрологического поста с измерениями расхода воды.

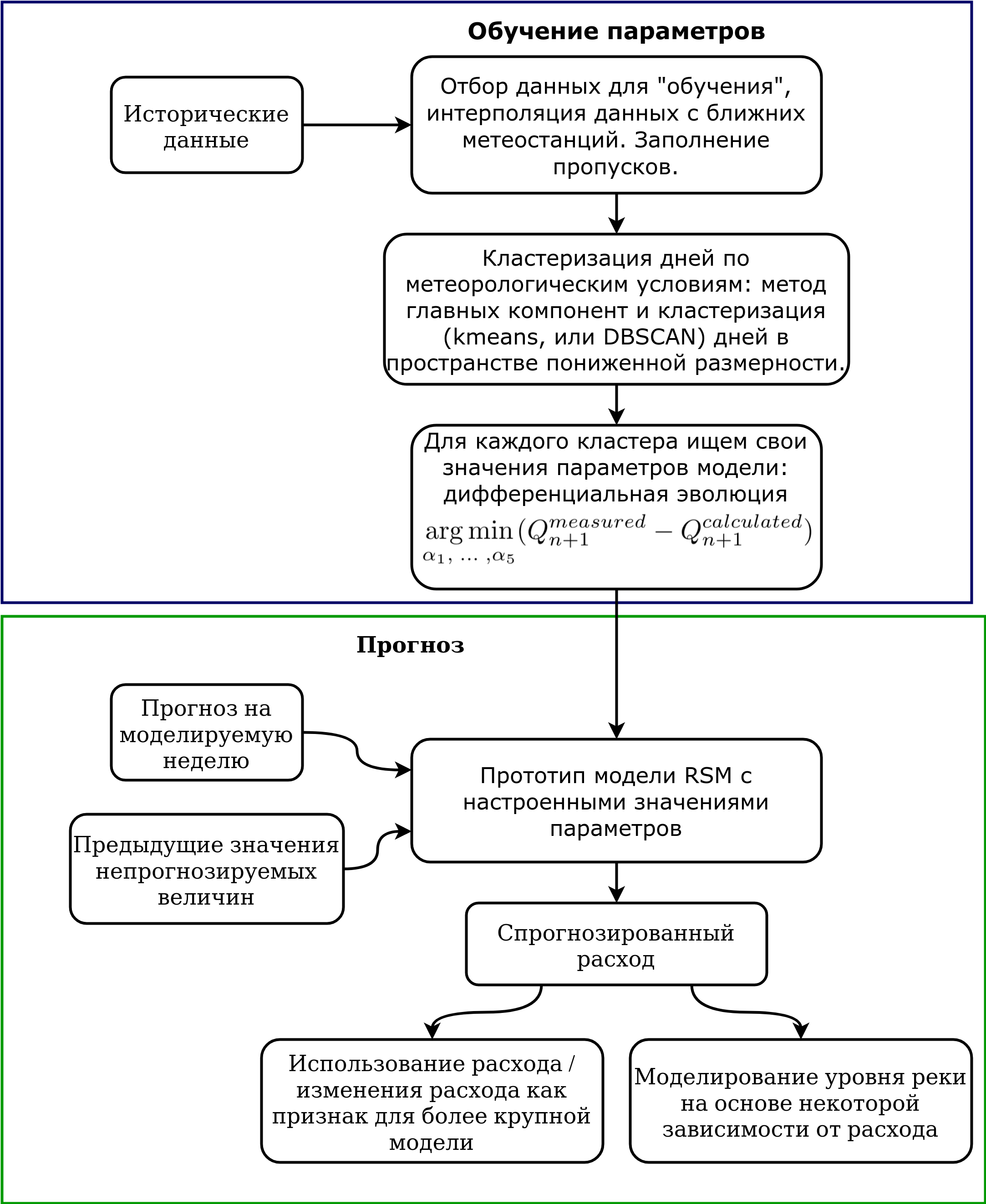
Слабым местом приложения подобной модели является то, что многие коэффициенты, входящие в неё, зависят от различных метеоусловий, а также связаны с климатом в регионе и орографическими свойствами бассейна. Если производить тюнинг модели (калибровку) на всех доступных данных сразу, то многие параметры будут оценены “в среднем”, и их возможные изменения, связанные с воздействием метеорологических факторов не будут учитываться. По этой причине мы решили выделить характерные метеорологические условия, произведя кластеризацию дней наблюдения по метеоизмерениям. Затруднением для подобной кластеризации была высокая размерность пространства: 8 измерений, описывающих различные метеорологические характеристики. Несмотря на то, что существуют подходы кластеризации в пространстве высоких размерностей, мы решили сначала понизить размерность исследуемого пространства, и лишь после этого производить кластеризацию. После использования метода главных компонент (PCA) и соответствующего преобразования входных массивов, классификация проводилась методом DBSCAN. Последующие операции по поиску параметров модели проводились для каждого кластера отдельно.

Для дальнейшего поиска параметров модели мы оптимизировали целевую функцию, определённую через модуль разности наблюдаемого расхода воды в створе и прогноза, вычисленного через введённую ранее модель, вычисленную на выбранных данных.

Оптимизация производится относительно коэффициентов и выполняется методом дифференциальной эволюции. Предполагается, что при обработке новых данных алгоритм будет сначала определять, к какому типу метеорологических условий относится обрабатываемый день, подбирать соответствующие этим условиям значения коэффициентов модели стока, и после этого вычислять расход воды. Схема комбинированной модели представлена на рисунке 9.

Последней (и не полностью решенной в рамках хакатона из-за дефицита времени) задачей является определение уровня реки в зависимости от расхода воды. Несмотря на то, что для большинства рек характерна взаимно-однозначная, хотя и нелинейная, зависимость между расходом и уровнем воды, реки, подверженные замерзанию и иным ледовым явлениям, имеют более сложные зависимости. Например, при вскрытии реки могут наблюдаться ледовые заторы, которые препятствуют прохождению воды вниз по течению. В таком случае наблюдается значительный рост уровня воды, но расход, определённый как объём воды, проходящий через сечение за единицу времени, становится незначительным из-за низких скоростей. Пример подобной зависимости для створа представлен на рисунке 10. 

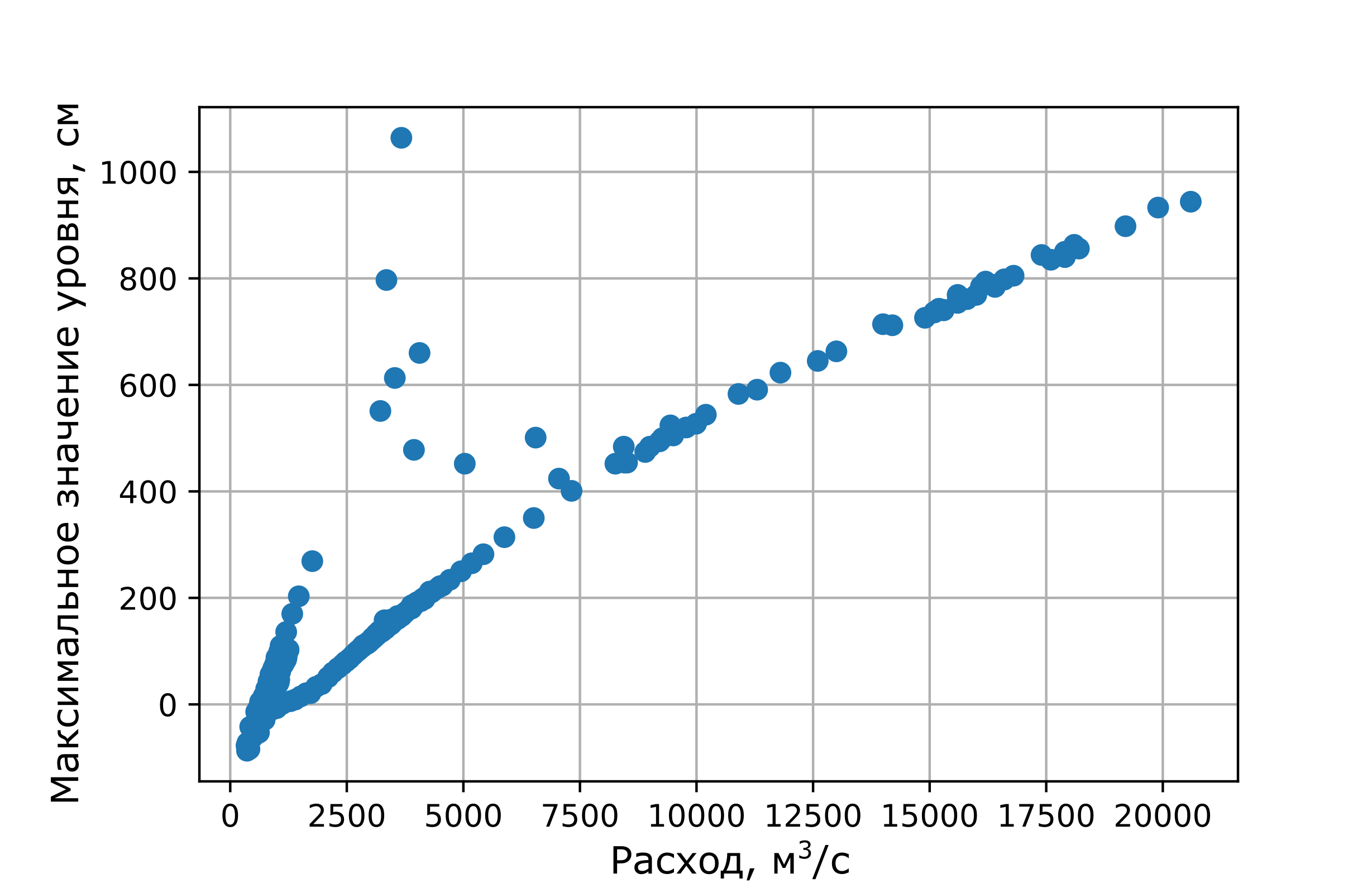
Для перерасчета расхода воды, предсказанного физической моделью, в уровни, была использована модель машинного обучения - случайный лес. В качестве предикторов использовались расход воды (количественный  предиктор) и месяц (категориальный). 

Заключение 

В результате был построен ансамбль из трёх моделей: прогнозирование временного ряда, многомерная регрессия на агрегированных метеоданных, физическое моделирование для одного гидропоста. Подготовленная модель превзошла конкурентов по leaderbord’у (см. картинку ниже). 

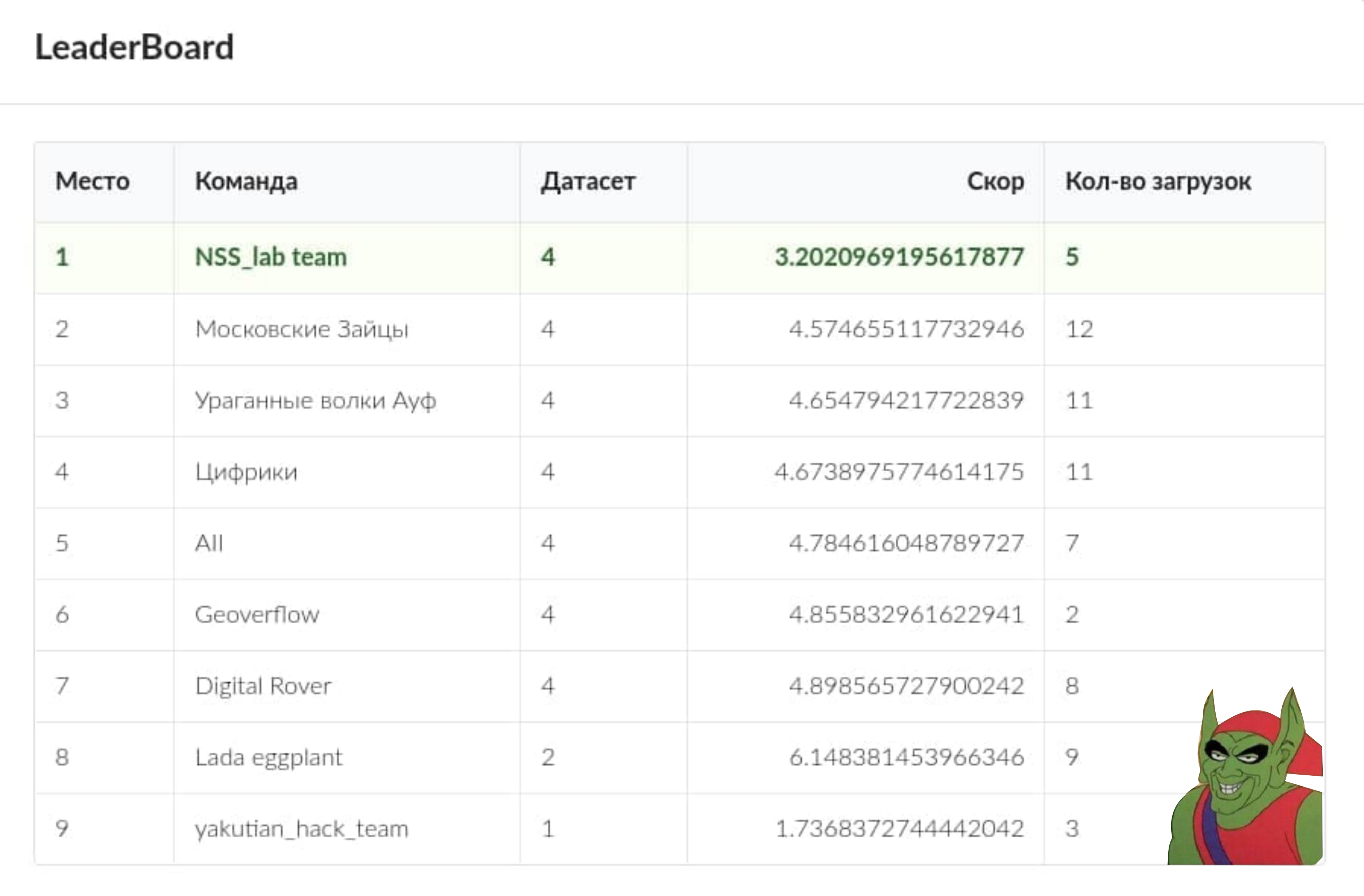
Надеемся, наш опыт поможет прочитавшим данную заметку, успешно выступить на своих хакатонах. Или, быть может, пригодится инженерам и программистам, перед которыми стоит задача реализовать систему прогнозирования для нужных им рек. 

Немного полезных ссылок:

• Репозиторий с представленным решением - emergency_datahack_nss

• AutoML фреймворк, который мы использовали - FEDOT

• Наша недавняя научная статья про фреймворк - Automated evolutionary approach for the design of composite machine learning pipelines

• Страничка с информацией о нашей лаборатории - NSS lab

• Новостная статья про победу на хакатоне - ITMO.News

• Репозиторий разрабатываемого web-модуля для фреймворка — FEDOT.Web

Команда “NSS_lab team”: 

• Борисова Юлия 

• Масляев Михаил

• Максимов Глеб

• Ревин Илья

• Сарафанов Михаил